판 이론

다음에 대한 시리즈 일부
연속체 역학
${\displaystyle J=-D{\frac {d\varphi }{dx}}}$ 픽의 확산 법칙
법 컨버지 미사 모멘텀 에너지 불평등 클라우시우스-듀헴 (엔트로피)
고체 역학 변형 탄력성 일직선의 가소성 후크의 법칙 스트레스 유한변형 무한 변형률 호환성. 벤딩 접촉 역학 마찰의 물질적 고장 이론 파단 역학
유체역학 유체 통계학 · 역학 아르키메데스의 원리 · 베르누이의 원리 나비에-스토크스 방정식 푸아세유 방정식 · 파스칼의 법칙 점도 (뉴턴어 · 비뉴턴어) 부력 · 믹싱 · 압력 액체 접착 모세관 작용 크로마토그래피 응집(화학) 표면장력 가스 대기 보일의 법칙 찰스의 법칙 복합가스법 픽의 법칙 게이 루삭의 법칙 그레이엄의 법칙 플라즈마
리히로지 점탄성 레호메트리 레히미터 스마트 유체 전기오류 자기 지질학 페로플루이드
과학자들 베르누이 보일 카우치 찰스 오일러 픽 게이 루삭 그레이엄 훅 뉴턴 나비에르 노울 파스칼 스톡스 트뤼셀
v t

연속역학에서 판 이론은 보의 이론을 그리는 평판의 역학을 수학적으로 기술한 것이다. 플레이트는 평면 치수에 비해 두께가 작은 평면 구조 요소로 정의된다.^[1] 판 구조물의 일반적인 두께 대 폭 비율은 0.1 미만이다.^{[citation needed]} 판 이론은 이 길이 척도의 차이를 이용하여 완전한 3차원 고체 역학 문제를 2차원 문제로 축소한다. 판 이론의 목적은 하중을 받는 판의 변형과 응력을 계산하는 것이다.

19세기 후반부터 발전해 온 수많은 판 이론 중 두 이론이 널리 받아들여져 공학에 사용되고 있다. 이것들은

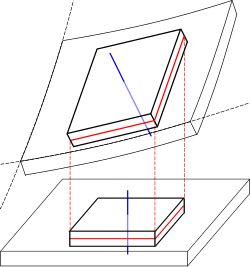
• 키르호프-러브 플레이트 이론(클래식 플레이트 이론)
• 플레이트의 Uflyand-Mindlin 이론 (일차 전단 플레이트 이론)

얇은 판에 대한 Kirchhoff-Love 이론

참고: 반복 지수를 요약하는 아인슈타인 종합 관례가 아래에 사용된다.

키르흐호프-러브 이론은 오일러-베르누엘리 빔 이론을 얇은 판으로 확장한 것이다. 이 이론은 1888년 사랑^[2](Love)이 키르흐호프가 제안한 가정을 이용해 개발한 이론이다. 3차원 판을 2차원 형태로 나타내기 위해 중간면(mid-surface plane)을 사용할 수 있다고 가정한다.

이 이론에서 이루어지는 다음과 같은 운동학적 가정들:^[3]

• 변형 후에도 중간점까지의 직선은 직선으로 유지된다.
• 변형 후 중간점까지 보통 직선은 중간점까지 보통으로 유지된다.
• 판 두께는 변형 중에 변하지 않는다.

변위장

Kirchhoff 가설은 변위장이 형태를 가지고 있다는 것을 암시한다.

where ${\displaystyle x_{1}}$ and ${\displaystyle x_{2}}$ are the Cartesian coordinates on the mid-surface of the undeformed plate, ${\displaystyle x_{3}}$ is the coordinate for the thickness direction, ${\displaystyle u_{1}^{0},u_{2}^{0}}$ are the in-plane displacements of t그는 중간 방향이고 $w{\displaystyle {}^{}}$ ${\displaystyle {0\mathrm{}}^{}}$ ${\$ w$^{0}$는 $x{\displaystyle {}_{}}$ ${\displaystyle {3\mathrm{}}_{}}$ ${\$ 방향에서$$ 중간 방향의 변위다$$.

${\displaystyle {\alpha }_{}}$ ${\$이(가) 정상의 회전각인 경우 키르흐호프-러브 이론 ${\displaystyle {\alpha }_{}}$ = ${\displaystyle {}_{,}^{}}$ ${\displaystyle {\mathrm{}}_{}^{}}$ 0.${\displaystyle \varphi _{\alpha }=w_{,\}^{0},},},},},},},}.$$}$

표면 중간(왼쪽)과 정상(오른쪽)의 변위

변형-변위 관계

판의 균주가 극미하고 표면의 중간 정규의 회전이 10° 미만인 상황의 경우 균주-변위 관계는 다음과 같다.

${\displaystyle {\begin{aligned}\varepsilon _{\alpha \beta }&={\tfrac {1}{2}}(u_{\alpha ,\beta }^{0}+u_{\beta ,\alpha }^{0})-x_{3}~w_{,\alpha \beta }^{0}\\\varepsilon _{\alpha 3}&=-w_{,\alpha }^{0}+w_{,\alpha }^{0}=0\\\varepsilon _{33}&=0\end{aligned}}}$

따라서 0이 아닌 유일한 변종은 평면 내 방향이다.

정상에서 표면 중간까지의 회전 범위가 10°~15°인 경우, 폰 카르만 변종을 사용하여 변형률 변위 관계를 근사하게 추정할 수 있다. 그러면 키르흐호프-러브 이론의 운동학적 가정은 다음과 같은 변종-변종 관계를 초래하게 된다.

${\displaystyle {\begin{aligned}\varepsilon _{\alpha \beta }&={\frac {1}{2}}(u_{\alpha ,\beta }^{0}+u_{\beta ,\alpha }^{0}+w_{,\alpha }^{0}~w_{,\beta }^{0})-x_{3}~w_{,\alpha \beta }^{0}\\\varepsilon _{\alpha 3}&=-w_{,\alpha }^{0}+w_{,\alpha }^{0}=0\\\varepsilon _{33}&=0\end{aligned}}}$

이 이론은 변형-변형 관계에서 이차적인 용어 때문에 비선형적이다.

평형 방정식

판의 평형 방정식은 가상 작업의 원리에서 도출할 수 있다. 판의 변종과 회전이 작은 상황의 경우, 비적재 판의 평형 방정식은 다음과 같이 주어진다.

${\displaystyle {\reasoned}N_{\alpha \beta \beta }&=0\\m_{\alpha \beta }&=0\ended}}\alpha \beta \beta }}}$

여기서 스트레스 결과 및 스트레스 모멘트 결과물은 다음과 같이 정의된다.

${\displaystyle N_{\alpha \beta }:=\int _{-h}^{h}\sigma _{\alpha \beta }~dx_{3}~;~~M_{\alpha \beta }:=\int _{-h}^{h}x_{3}~\sigma _{\alpha \beta }~dx_{3}}$

그리고 플레이트의 두께는 $(\displaystyle 2시간)$이다$.$ ${\displaystyle {\alpha }_{}}$ ${\$의 양이 스트레스다$$.

플레이트가 표면 중간까지 정상이고 $양{\displaystyle {}_{}}$ x$$ ${\displaystyle {3\mathrm{}}_{}}$ ${\$ 방향으로$$ 향하는 외부 분산 부하 $q{\displaystyle (x}$) ${\displaystyle q(x)}$에 의해 적재되면 가상 작업의 원리는 평형 방정식으로 이어진다.

적당한 회전의 경우, 변형-변위 관계는 폰 카르만 형태를 취하며 평형 방정식은 다음과 같이 표현할 수 있다.

${\displaystyle {\reasoned}N_{\\알파 \beta \beta }&=0\\m_\\beta \beta }+[N_{\alpha \beta \beta \w_{},\beta }^{0}]_{,\alpha }-q&=0}}}정렬}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}?$

경계 조건

판 이론의 평형 방정식을 푸는 데 필요한 경계조건은 가상작업 원리의 경계용어로부터 얻을 수 있다.

작은 변종과 작은 회전의 경우 경계조건은 다음과 같다.

${\displaystyle {\begin{aligned}n_{\alpha }~N_{\alpha \beta }&\quad \mathrm {or} \quad u_{\beta }^{0}\\n_{\alpha }~M_{\alpha \beta ,\beta }&\quad \mathrm {or} \quad w^{0}\\n_{\beta }~M_{\alpha \beta }&\quad \mathrm {or} \quad w_{,\alpha }^{0}\end{aligned}}}$

$n{\displaystyle {}_{}}$ ${\displaystyle {\alpha }_{}}$ ${\displaystyle M{}_{}{}_{}}$ ${\displaystyle {\alpha }_{}}$ ${\displaystyle {\beta }_{}}$ ,${\displaystyle {\beta }_{}}$ ${\$M_${\alpha \beta$}}}은$($는) 유효 전단력이라는 점에$$ 유의한다.

스트레스-스트레인 관계

선형 탄성 Kirchhoff 플레이트의 응력-변형 관계는 다음과 같다.

${\displaystyle {\begin{bmatrix}\sigma _{11}\\\sigma _{22}\\\sigma _{12}\end{bmatrix}}={\begin{bmatrix}C_{11}&C_{12}&C_{13}\\C_{12}&C_{22}&C_{23}\\C_{13}&C_{23}&C_{33}\end{bmatrix}}{\begin{bmatrix}\varepsilon _{11}\\\varepsilon _{22}\\\varepsilon _{12}\end{bmatrix}}}$

${\displaystyle {\alpha }_{}}$ ${\displaystyle 3_{}}$ ${\$ 3$}$과 $\sigma {\displaystyle {}_{}}$ ${\displaystyle {33}_{}}$ ${\$은 평형 방정식에 나타나지 않기$$ 때문에 이러한 양이 운동량 균형에 영향을 미치지 않고 무시된다고 암묵적으로 가정한다.

평형 방정식에 들어가는 스트레스와 모멘트 결과물을 가지고 작업하는 것이 더 편리하다. 이것들은 에 의한 변위와 관련이 있다.

${\displaystyle {\begin{bmatrix}N_{11}\\N_{22}\\N_{12}\end{bmatrix}}=\left\{\int _{-h}^{h}{\begin{bmatrix}C_{11}&C_{12}&C_{13}\\C_{12}&C_{22}&C_{23}\\C_{13}&C_{23}&C_{33}\end{bmatrix}}~dx_{3}\right\}{\begin{bmatrix}u_{1,1}^{0}\\u_{2,2}^{0}\\{\frac {1}{2}}~(u_{1,2}^{0}+u_{2,1}^{0})\end{bmatrix}}}$

그리고

${\displaystyle {\begin{bmatrix}M_{11}\\M_{22}\\M_{12}\end{bmatrix}}=-\left\{\int _{-h}^{h}x_{3}^{2}~{\begin{bmatrix}C_{11}&C_{12}&C_{13}\\C_{12}&C_{22}&C_{23}\\C_{13}&C_{23}&C_{33}\end{bmatrix}}~dx_{3}\right\}{\begin{bmatrix}w_{,11}^{0}\\w_{,22}^{0}\\w_{,12}^{0}\end{bmatrix}}\,.}$

확장 강성은 수량이다.

${\displaystyle A_{\alpha \beta }:=\int _{-h}^{h}C_{\alpha \beta \beta }~dx_{3}}}}}$

휨강성(휨강성이라고도 함)은 수량이다.

${\displaystyle D_{\alpha \beta }:=\int _{-h}^{h}x_{3}^{2}~C_{\alpha \beta }~dx_{3}}}}}}}}}{3}}}}}}}}}}$

등방성 및 균질 Kirchhoff 판

등방성 및 균질 판의 경우 응력-변형 관계는 다음과 같다.

${\displaystyle {\begin{bmatrix}\sigma _{11}\\\sigma _{22}\\\sigma _{12}\end{bmatrix}}={\cfrac {E}{1-\nu ^{2}}}{\begin{bmatrix}1&\nu &0\\\nu &1&0\\0&0&1-\nu \end{bmatrix}}{\begin{bmatrix}\varepsilon _{11}\\\varepsilon _{22}\\\varepsilon _{12}\end{bmatrix}}\,.}$

이러한 스트레스에 해당하는 순간은

${\displaystyle {\begin{bmatrix}M_{11}\\M_{22}\\M_{12}\end{bmatrix}}=-{\cfrac {2h^{3}E}{3(1-\nu ^{2})}}~{\begin{bmatrix}1&\nu &0\\\nu &1&0\\0&0&1-\nu \end{bmatrix}}{\begin{bmatrix}w_{,11}^{0}\\w_{,22}^{0}\\w_{,12}^{0}\end{bmatrix}}}$

순수 벤딩

$u{\displaystyle {}_{}^{}}$ ${\displaystyle {1\mathrm{}}_{}^{}}$ ${\displaystyle {\mathrm{}}_{}^{}}$ ${\$ 및$$ ${\displaystyle {\mathrm{}}_{}^{}}$ 2 0 ${\$은(는) 순수한 휨 조건에서 0이다$$. 등방성의 경우, 순 벤딩 아래의 균질 플레이트는 다음과 같다.

${\displaystyle {\frac {\partial ^{4}w}{\partial x_{1}^{4}}}+2{\frac {\partial ^{4}w}{\partial x_{1}^{2}\partial x_{2}^{2}}}+{\frac {\partial ^{4}w}{\partial x_{2}^{4}}}=0\quad {\text{where}}\quad w:=w^{0}\,.}$

색인 표기법에서,

${\displaystyle w_{,1111}^{0}+2~w_{,1212}^{0}+w_{,2222}^{0}=0\,.}$

직접 텐서 표기법에서 지배 방정식은 다음과 같다.

횡하중

축변형이 없는 횡하중 판의 경우, 지배방정식의 형태는 다음과 같다.

${\displaystyle {\frac {\partial ^{4}w}{\partial x_{1}^{4}}}+2{\frac {\partial ^{4}w}{\partial x_{1}^{2}\partial x_{2}^{2}}}+{\frac {\partial ^{4}w}{\partial x_{2}^{4}}}=-{\frac {q}{D}}}$

어디에

${\displaystyle D:={\cfrac {2h^{3}E}{3(1-\nu ^{2})}}\,.}$

색인 표기법에서,

${\displaystyle w_{,1111}^{0}+2\,w_{,1212}^{0}+w_{,2222}^{0}=-{\frac {q}{D}}}}}}}}$

그리고 직접 표기법

원통형 좌표$({\displaystyle r}$, ${\displaystyle \theta }$, ${\displaystyle z}$) ${\displaystyle(r,\theta ,z)}$에서$,$ 지배 방정식은 다음과 같다.

${\displaystyle {\frac {1}{r}}{\cfrac {d}{dr}}\left[r{\cfrac {d}{dr}}\left\{{\frac {1}{r}}{\cfrac {d}{dr}}\left(r{\cfrac {dw}{dr}}\right)\right\}\right]=-{\frac {q}{D}}\,.}$

직교방성 및 균질 Kirchhoff 판

직교이방성 판의 경우

${\displaystyle {\begin{bmatrix}C_{11}&C_{12}&C_{13}\\C_{12}&C_{22}&C_{23}\\C_{13}&C_{23}&C_{33}\end{bmatrix}}={\cfrac {1}{1-\nu _{12}\nu _{21}}}{\begin{bmatrix}E_{1}&\nu _{12}E_{2}&0\\\nu _{21}E_{1}&E_{2}&0\\0&0&2G_{12}(1-\nu _{12}\nu _{21})\end{bmatrix}}\,.}$

그러므로

${\displaystyle {\bmatrix}A_{11}&A_{12}&A_{13}\\A_{21}&A_{22}&A_{23}\\A_{31}&A_{32}&A_{33}\end{bmatrix}}={\cfrac {2h}{1-\nu _{12}\nu _{21}}}{\begin{bmatrix}E_{1}&\nu _{12}E_{2}&0\\\nu _{21}E_{1}&E_{2}&0\\0&0&2G_{12}(1-\nu _{12}\nu _{21})\end{bmatrix}}}$

그리고

${\displaystyle {\begin{bmatrix}D_{11}&D_{12}&D_{13}\\D_{21}&D_{22}&D_{23}\\D_{31}&D_{32}&D_{33}\end{bmatrix}}={\cfrac {2h^{3}}{3(1-\nu _{12}\nu _{21})}}{\begin{bmatrix}E_{1}&\nu _{12}E_{2}&0\\\nu _{21}E_{1}&E_{2}&0\\0&0&2G_{12}(1-\nu _{12}\nu _{21})\end{bmatrix}}\,.}$

횡하중

단위 면적당$$ 분산 하중 $q{\displaystyle }$ ${\displaystyle q}$에 의해 횡방향으로 적재된 직교이방성 Kirchhoff 판의 지배 방정식은 다음과 같다.

${\displaystyle D_{x}w_{,1111}^{0}+2D_{xy}w_{1122}^{0}+D_{y}w_{,2222}^{0}=-q}$

어디에

${\displaystyle {\begin}D_{x}&=D_{11}={\frac {2h^{3}E_{1}{3}1}{3}{3}}}}{3(-1-\nu _{12}\nu_{21}}}\\\\\\\\\\\\\\D_{y}&=D_{22}={\frac {2h^{3}E_{2}}{3(1-\nu _{12}\nu _{21})}}\\D_{xy}&=D_{33}+{\tfrac {1}{2}}(\nu _{21}D_{11}+\nu _{12}D_{22})=D_{33}+\nu _{21}D_{11}={\frac {4h^{3}G_{12}}}{3}}}}{3}+{{2h^{3}\nu_{21}E_{1}}}}}{3(-1-\nu _{12}}}}}}}}}}}}}}}}}},\end{{ned{no}}}}}}}}}}}}}}}}}}}}}}).$

얇은 Kirchhoff 판의 역학

판의 동적 이론은 판의 파장의 전파를 결정하며, 기립파 및 진동 모드에 대한 연구도 한다.

지배 방정식

키르흐호프-러브 플레이트의 역학관계에 대한 지배 방정식은 다음과 같다.

여기서, 밀도 $\rho {\displaystyle }$= ${\displaystyle \rho }$( ${\displaystyle x}$) ${\displaystyle \rho =\rho (x)}$인 플레이트의 경우$,$

${\displaystyle J_{1}:=\int _{-h}^{h}\rho ~dx_{3}=2~\rho ~h~;~~J_{3}:=\int _{-h}^{h}x_{3}^{2}~\rho ~dx_{3}={\frac {2}{3}}~\rho ~h^{3}}$

그리고

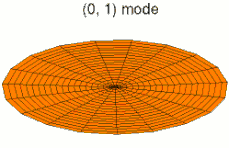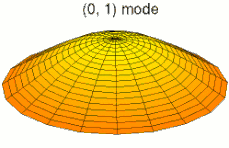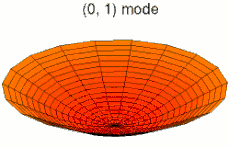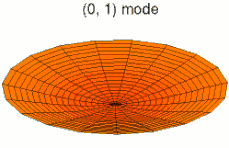
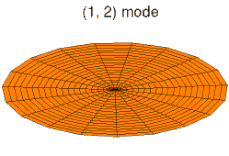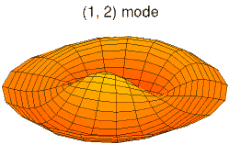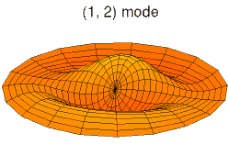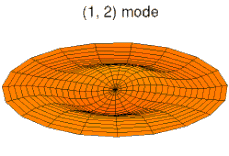
${\displaystyle {\dot {u}}_{i}={\frac {\partial u_{i}}{\partial t}}~;~~{\ddot {u}}_{i}={\frac {\partial ^{2}u_{i}}{\partial t^{2}}}~;~~u_{i,\alpha }={\frac {\partial u_{i}}{\partial x_{\alpha }}}~;~~u_{i,\alpha \beta }={\frac {\partial ^{2}u_{i}}{\partial x_{\alpha }\partial x_{\beta }}}}$

아래 그림은 원형 판의 진동 모드를 보여준다.

• 

  모드 k = 0, p = 1

• 

  모드 k = 1, p = 2

등방성 판

지배 방정식은 평면 내 변형을 무시할 수 있고 형태를 가질 수 있는 등방성 및 동종 판에 대해 상당히 단순화된다.

${\displaystyle D\,\left({\frac {\partial ^{4}w^{0}}{\partial x_{1}^{4}}}+2{\frac {\partial ^{4}w^{0}}{\partial x_{1}^{2}\partial x_{2}^{2}}}+{\frac {\partial ^{4}w^{0}}{\partial x_{2}^{4}}}\right)=-q(x_{1},x_{2},t)-2\rho h\,{\frac {\partial ^{2}w^{0}}{\partial t^{2}}}\,.}$

여기서 $D{\displaystyle }$ ${\displaystyle D}$은 플레이트의 휨 강성이다. 두께가 ${\displaystyle \mathrm{2시간}}$ ${\displaystyle 2h}$인 균일한 플레이트의 경우$,$

${\displaystyle D:={\cfrac {2h^{3}E}{3(1-\nu ^{2})}}\,.}$

직접 표기법

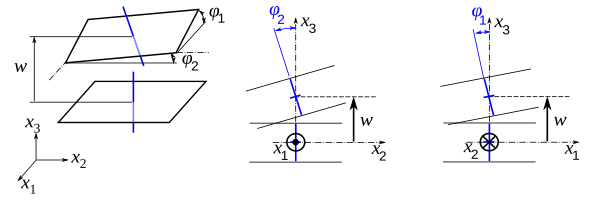
두꺼운 판에 대한 Uflyand-Mindlin 이론

참고: 반복 지수를 요약하는 아인슈타인 종합 관례가 아래에 사용된다.

두꺼운 판의 이론 또는 야코프 S. 우플라이랜드의^[4] 이론(자세한 것은 엘리사코프의 핸드북^[5] 참조), 레이먼드 민들린과^[6] 에릭 라이스너에서, 중간표면까지의 정상은 직선으로 유지되지만 반드시 중간표면에 수직인 것은 아니다. $\phi {\displaystyle {}_{}}$ ${\$및$$ ${\displaystyle {\phi \mathrm{}}_{}}$ 2 ${\$}가 x ${\displaystyle {3\mathrm{}}_{}}$ ${\$ 축으로$$ 중간 표면이 만드는 각도를 지정하면 다음과$$ 같이 된다.

${\displaystyle \varphi _{1}\neq w_{,1}~\varphi _{2}\neq w_{,2}}:$

그렇다면 민들린-라이스너 가설은 다음과 같은 것을 내포하고 있다.

변형-변위 관계

판규격의 회전량에 따라 균주에 대한 두 가지 다른 근사치를 기본 운동학적 가정으로부터 도출할 수 있다.

작은 변종과 작은 회전의 경우, Mindlin-Rissner 판의 변형-변형 관계는 다음과 같다.

${\displaystyle {\begin{aligned}\varepsilon _{\alpha \beta }&={\frac {1}{2}}(u_{\alpha ,\beta }^{0}+u_{\beta ,\alpha }^{0})-{\frac {x_{3}}{2}}~(\varphi _{\alpha ,\beta }+\varphi _{\beta ,\alpha })\\\varepsilon _{\alpha 3}&={\cfrac {1}{2}}\left(w_{,\alpha }^{0}-\varphi _{\alpha }\right)\\\varepsilon _{33}&=0\end{aligned}}}$

판 두께에 걸친 전단 변형률, 즉 전단 응력은 이 이론에서 소홀히 다루지 않는다. 그러나 전단변형은 판 두께에 걸쳐 일정하다. 단순한 판 기하학적 구조에서도 전단 응력이 포물선인 것으로 알려져 있어 정확할 수 없다. 전단 변형률의 부정확성을 설명하기 위해 ${\displaystyle }$ 보정 계수( ( ${\displaystyle \kappa$ $\})$를 적용하여 이론에 의해 정확한 내부 에너지 양을 예측한다. 그러면.

${\displaystyle \varepsilon _{\properties 3}={\pack {1}{1}2}}~\cappa ~\좌측(w_{,\pa }^{0}-\varphi _{\pa }\pright)}$

평형 방정식

평형 방정식은 판에 기대되는 휨의 양에 따라 약간 다른 형태를 가진다. 판의 변종과 회전이 작은 상황에서 민들린-리스너 판의 평형 방정식은 다음과 같다.

상기 방정식의 결과 전단력은 다음과 같이 정의된다.

${\displaystyle Q_{\alpha }:=\kappa ~\int _{-h}^{h}\sigma _{\alpha 3}~dx_{3}\,}$

경계 조건

경계조건은 가상작업의 원칙에서 경계용어로 표시된다.

외력만이 판의 상단 표면에 수직력일 경우 경계조건은 다음과 같다.

${\displaystyle {\begin{aligned}n_{\alpha }~N_{\alpha \beta }&\quad \mathrm {or} \quad u_{\beta }^{0}\\n_{\alpha }~M_{\alpha \beta }&\quad \mathrm {or} \quad \varphi _{\alpha }\\n_{\alpha }~Q_{\alpha }&\quad \mathrm {or} \quad w^{0}\end{aligned}}}$

구성 관계

선형 탄성 Mindlin-Rissner 판의 응력-변형 관계는 다음과 같다.

${\displaystyle {\begin{aligned}\sigma _{\alpha \beta }&=C_{\alpha \beta \gamma \theta }~\varepsilon _{\gamma \theta }\\\sigma _{\alpha 3}&=C_{\alpha 3\gamma \theta }~\varepsilon _{\gamma \theta }\\\sigma _{33}&=C_{33\gamma \theta }~\varepsilon _{\gamma \theta }\end{aligned}}}$

$\sigma {\displaystyle {}_{}}$ ${\$은 평형 방정식에 나타나지 않기$$ 때문에 모멘텀 균형에 아무런 영향을 미치지 않고 무시된다고 암묵적으로 가정한다. 이러한 가정을 평면응력 가정이라고도 한다. 직교방성 물질에 대한 나머지 응력-변형 관계는 행렬 형태로 다음과 같이 기록할 수 있다.

${\displaystyle {\begin{bmatrix}\sigma _{11}\\\sigma _{22}\\\\sigma _{23}\\\\nd{bmatrix}}}={\gin{bmatrix}C_{12}&0&0&0\\\\\\\n0\\\\\\n0\\\\\\\\\\\\\\\\\\\C_{12}&C_{22}&0&0&0\\0&0&C_{44}&0&0\\0&0&0&C_{55}&0\\0&0&0&0&C_{66}\end{bmatrix}}{\begin{bmatrix}\varepsilon _{11}\\\varepsilon _{22}\\\varepsilon _{23}\\\varepsilon _{31}\\\varepsilon _{12}\end{bmatrix}}}$

그러면.

${\displaystyle {\begin{bmatrix}N_{11}\\N_{22}\\N_{12}\end{bmatrix}}=\left\{\int _{-h}^{h}{\begin{bmatrix}C_{11}&C_{12}&0\\C_{12}&C_{22}&0\\0&0&C_{66}\end{bmatrix}}~dx_{3}\right\}{\begin{bmatrix}u_{1,1}^{0}\\u_{2,2}^{0}\\{\frac {1}{2}}~(u_{1,2}^{0}+u_{2,1}^{0})\end{bmatrix}}}$

그리고

${\displaystyle {\begin{bmatrix}M_{11}\\M_{22}\\M_{12}\end{bmatrix}}=-\left\{\int _{-h}^{h}x_{3}^{2}~{\begin{bmatrix}C_{11}&C_{12}&0\\C_{12}&C_{22}&0\\0&0&C_{66}\end{bmatrix}}~dx_{3}\right\}{\begin{bmatrix}\varphi _{1,1}\\\varphi _{2,2}\\{\frac {1}{2}}~(\varphi _{1,2}+\varphi _{2,1})\end{bmatrix}}}$

전단 항의 경우

${\displaystyle {\begin{bmatrix}Q_{1}\\Q_{2}\end{bmatrix}}={\cfrac {\kappa }{2}}\left\{\int _{-h}^{h}{\begin{bmatrix}C_{55}&0\\0&C_{44}\end{bmatrix}}~dx_{3}\right\}{\begin{bmatrix}w_{,1}^{0}-\varphi _{1}\\w_{,2}^{0}-\varphi _{2}\end{bmatrix}}}$

확장 강성은 수량이다.

${\displaystyle A_{\alpha \beta }:=\int _{-h}^{h}C_{\alpha \beta \beta }~dx_{3}}}}}$

벤딩 강성은 수량이다.

${\displaystyle D_{\alpha \beta }:=\int _{-h}^{h}x_{3}^{2}~C_{\alpha \beta }~dx_{3}}}}}}}}}{3}}}}}}}}}}$

등방성 및 균질 유플라이앤드민들린 판

균일하게 두껍고 균질하며 등방성 평면의 응력-변형성 관계는 다음과 같다.

${\displaystyle {\begin{bmatrix}\sigma _{11}\\\sigma _{22}\\\sigma _{12}\end{bmatrix}}={\cfrac {E}{1-\nu ^{2}}}{\begin{bmatrix}1&\nu &0\\\nu &1&0\\0&0&1-\nu \end{bmatrix}}{\begin{bmatrix}\varepsilon _{11}\\\varepsilon _{22}\\\varepsilon _{12}\end{bmatrix}}\,.}$

$여기$서 E ${\displaystyle E}$은 영의 계량형이고, $\nu {\displaystyle }$ ${\displaystyle \nu}$은 포아송의 비율이며,$$α$$ $\beta {\displaystyle {}_{}}$ {\$displaystyle \varepsilon _{\alpha \beta }}}}$은 평면 내 변종이다$$. through thickness 전단 응력 및 균주는 다음에 의해 관련된다.

${\displaystyle \sigma _{31}=2G\varepsilon _{31}\quad {\text{and}}\quad \sigma _{32}=2G\varepsilon _{32}}}}}$

여기서 $G{\displaystyle }$= ${\displaystyle E}$/${\displaystyle }$( ${\displaystyle 2}$( (${\displaystyle 1}$ + ${\displaystyle )}$ )${\displaystyle }$) ${\displaystyle G=E/(2+\nu )}$은 전단 계수다.

구성 관계

등방성 Mindlin-Rissner 판에 대한 응력 결과와 일반화된 변위 사이의 관계는 다음과 같다.

${\displaystyle {\begin{bmatrix}N_{11}\\N_{22}\\N_{12}\end{bmatrix}}={\cfrac {2Eh}{1-\nu ^{2}}}{\begin{bmatrix}1&\nu &0\\\nu &1&0\\0&0&1-\nu \end{bmatrix}}{\begin{bmatrix}u_{1,1}^{0}\\u_{2,2}^{0}\\{\frac {1}{2}}~(u_{1,2}^{0}+u_{2,1}^{0})\end{bmatrix}}\,,}$

${\displaystyle {\begin{bmatrix}M_{11}\\M_{22}\\M_{12}\end{bmatrix}}=-{\cfrac {2Eh^{3}}{3(1-\nu ^{2})}}{\begin{bmatrix}1&\nu &0\\\nu &1&0\\0&0&1-\nu \end{bmatrix}}{\begin{bmatrix}\varphi _{1,1}\\\varphi _{2,2}\\{\frac {1}{2}}(\varphi _{1,2}+\varphi _{2,1})\end{bmatrix}}\,,}$

그리고

${\displaystyle {\begin{bmatrix}Q_{1}\Q_{2}\end{bmatrix}}=\cappa Gh{begin{bmatrix}w_{1}^{0}-\varphi _{0}-{0}-}-{bmatrix\}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}.}$

벤딩 강성은 양으로 정의된다.

${\displaystyle D={\cfrac {2Eh^{3}{3}{3}}{3(1-\nu ^{2}}}}\,.}$

두께 $H{\displaystyle }$ ${\displaystyle H}$의 플레이트에 대해 벤딩 강성은 형태를 가진다$.$

${\displaystyle D={\cfrac {EH^{3}}{12(1-\nu ^{2}}}}\,.}$

여기서 h${\displaystyle }$= ${\displaystyle H\frac{}{}}$ ${\displaystyle \frac{2}{}}$ ${\$

지배 방정식

만약 우리가 판의 평면 내 확장을 무시한다면, 지배 방정식은

${\displaystyle {\reasoned}M_{\alpha \beta ,\beta }-Q_{\alpha }=0&=\Q_{\alpha,\alpha }+q&=0\,\end{정렬}}}$

${\displaystyle {0\mathrm{}}^{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$, ${\displaystyle {2\mathrm{}}_{}}$ 2$${\$displaystyle$ w$^{0},\varphi _${1$},\varphi _{2$}}의 일반화된 변형에 비추어 볼 때$,$ 세 가지 지배 방정식은 다음과 같다.

직사각형 플레이트의 가장자리를 따라 있는 경계 조건은 다음과 같다.

${\displaystyle {\begin{aligned}{\text{simply supported}}\quad &\quad w^{0}=0,M_{11}=0~({\text{or}}~M_{22}=0),\varphi _{1}=0~({\text{or}}~\varphi _{2}=0)\\{\text{clamped}}\quad &\quad w^{0}=0,\varphi _{1}=0,\varphi _{2}=0\,.\end{정렬}}}$

등방성 캔틸레버 판에 대한 레이스너-스타인 정적 이론

일반적으로 판 이론을 이용한 칸틸레버 판에 대한 정확한 해법은 상당히 관련되어 있으며 문헌에서 정확한 해법은 거의 찾아볼 수 없다. Reissner와 Stein은^[7] 생베난트 판 이론과 같은 오래된 이론보다 개선된 캔틸레버 판에 대해 단순화된 이론을 제공한다.

라이스너-슈타인 이론은 형태의 횡변위장을 가정한다.

${\displaystyle w(x,y)=w_{x}(x)+y\,\theta _{x}(x)\,}$

판에 대한 지배 방정식은 두 개의 결합된 일반 미분 방정식으로 감소한다.

어디에

${\displaystyle {\begin{aligned}q_{1}(x)&=\int _{-b/2}^{b/2}q(x,y)\,{\text{d}}y~,~~q_{2}(x)=\int _{-b/2}^{b/2}y\,q(x,y)\,{\text{d}}y~,~~n_{1}(x)=\int _{-b/2}^{b/2}n_{x}(x,y)\,{\text{d}}y\\n_{2}(x)&=\int _{-b/2}^{b/2}y\,n_{x}(x,y)\,{\text{d}}y~,~~n_{3}(x)=\int _{-b/2}^{b/2}y^{2}\,n_{x}(x,y)\,{\text{d}}y\,.\end{정렬}}}$

$x{\displaystyle }$= ${\displaystyle 0}$ ${\displaystyle x=0$에서 빔은 클램프되므로 경계 조건은

${\displaystyle w(0,y)={\cfrac {dw}{dx}}{\Bigr }_{x=0}=0\qquad \implies \qquad w_{x}(0)={\cfrac {dw_{x}}{dx}}{\Bigr }_{x=0}=\theta _{x}(0)={\cfrac {d\theta _{x}}{dx}}{\Bigr }_{x=0}=0\,.}$

${\displaystyle x}$${\displaystyle }$= ${\displaystyle x=a}$의 경계 조건은

${\displaystyle {\begin{aligned}&bD{\cfrac {d^{3}w_{x}}{dx^{3}}}+n_{1}(x){\cfrac {dw_{x}}{dx}}+n_{2}(x){\cfrac {d\theta _{x}}{dx}}+q_{x1}=0\\&{\frac {b^{3}D}{12}}{\cfrac {d^{3}\theta _{x}}{dx^{3}}}+\left[n_{3}(x)-2bD(1-\nu )\right]{\cfrac {d\theta _{x}}{dx}}+n_{2}(x){\cfrac {dw_{x}}{dx}}+t=0\\&bD{\cfrac {d^{2}w_{x}}{dx^{2}}}+m_{1}=0\quad ,\quad {\frac {b^{3}}{12}}{\cfrac {d^{2}\theta _{x}{dx^{2}}+m_{2}}}=0\end{aigned}}$

어디에

${\displaystyle {\begin{aligned}m_{1}&=\int _{-b/2}^{b/2}m_{x}(y)\,{\text{d}}y~,~~m_{2}=\int _{-b/2}^{b/2}y\,m_{x}(y)\,{\text{d}}y~,~~q_{x1}=\int _{-b/2}^{b/2}q_{x}(y)\,{\text{d}}y\\t&=q_{x2}+m_{3}}=\int _{-b/2}^{b/2}y\,q_{x}(y)\,{\text{d}y+\,{-b/2}^{b/2}m_{xy}(y)\,{\text{d}y}y}\,\end{정렬}}}$

라이스너-슈타인 칸틸레버 판 방정식의 도출

균일한 두께 $h{\displaystyle }$ ${\displaystyle h}$의 얇은 직사각형 판의 휨 변형 에너지는 다음과$$ 같다. ${\displaystyle U={\frac {1}{2}}\int _{0}^{a}\int _{-b/2}^{b/2}D\left\{\left({\frac {\partial ^{2}w}{\partial x^{2}}}+{\frac {\partial ^{2}w}{\partial y^{2}}}\right)^{2}+2(1-\nu )\left[\left({\frac {\partial ^{2}w}{\partial x\partial y}}\right)^{2}-{\frac {\partial ^{2}w}{\partial x^{2}}}{\frac {\partial ^{2}w}{\partial y^{2}}}\right]\right\}{\text{d}x{\text{d}y}$ 여기서 $w{\displaystyle }$ ${\displaystyle w}$은 가로 변위, ${\displaystyle a}$은(는) 길이$$, $b{\displaystyle }$ ${\displaystyle b}$은(는) 너비, $\nu {\displaystyle }$ ${\displaystyle \nu}$은(는) 포아송 비율, $E{\displaystyle }$ ${\$disson의 $계수$, 그리고 E {\$displaystymuluse}$은 영의 계수 ${\displaystyle D={\frac {Eh^{3}}{12(1-\nu )}}.}$ 가로 하중 $q{\displaystyle }$ ${\displaystyle (x}$, y${\displaystyle }$) ${\displaystyle q(x,y)}($단위 길이당)의 잠재적 에너지는 ${\dapplaystyle P_{q}=\int _{0}^{a}\int _{-b/2}q(x,y)\,w(x,y)\\\text{d}x{d}y\,}$ 평면 내 부하 $n{\displaystyle {}_{}}$ ${\displaystyle x_{}}$ (${\displaystyle {}_{}x}$, ${\displaystyle y}$) ${\displaystyle n_{x}(x,y)}($단위 폭당)의 잠재적 에너지는 ${\displaystyle P_{n}={\frac {1}{2}}\int _{0}^{a}\int _{-b/2}^{b/2}n_{x}(x,y)\,\left({\frac {\partial w}{\partial x}}\right)^{2}\,{\text{d}}x{\text{d}}y\,.}$ 팁 힘 $q{\displaystyle {}_{}}$ ${\displaystyle {}_{}y}$ )$$ x (y ) $displaystyle q_{x}(y)}($단위 폭당)의 잠재적 에너지와 휨모멘트 ${\displaystyle m_{}}$ x ${\displaystyle {}_{}y}$) ${\displaystyle m_{xy}(y)}$ $및$ ${\displaystyle m_{}}$ ${\displaystyle {}_{}y)}$ ${\displaystystym m_{xy}(y)}($y)}($$y)}(단위 폭당)은 다음과 같다. ${\displaystyle P_{t}=\int _{-b/2}^{b/2}\left(q_{x}(y)\,w(x,y)-m_{x}(y)\,{\frac {\partial w}{\partial x}}+m_{xy}(y)\,{\frac {\partial w}{\partial y}}\right){\text{d}}x{\text{d}}y\,.}$ 에너지의 균형은 총 에너지가 ${\displaystyle W=U-(P_{q}+P_{n}+P_{t}\,}$ 리세너-슈타인의 변위 추정에 따라 ${\displaystyle U=\int_{0}^{a}{\frac {bD}{24}}\좌측[{\cfrac {d^{d^{2}w_{x}}{dx^{2}}\우측)^{2}+b^{2}^{2}}\왼쪽 \ft^{d^{2}\theta _{dx^{2}}}\오른쪽)^{2}+24(1-\nu )\왼쪽 \d\theac {d}{dx}\{dx}\right]\\\\\\\\\text{d}}}}}$ ${\displaystyle P_{q}=\int _{0}^{a}\left[\left(\int _{-b/2}^{b/2}q(x,y)\,{\text{d}}y\right)w_{x}+\left(\int _{-b/2}^{b/2}yq(x,y)\,{\text{d}}y\right)\theta _{x}\right]\,dx\,,}$ ${\displaystyle {\reasoned}P_{n}&={\frac {1}{2}}\int _{0}^{a}\left[\left(\int _{-b/2}^{b/2}n_{x}(x,y)\,{\text{d}}y\right)\left({\cfrac {dw_{x}}{dx}}\right)^{2}+\left(\int _{-b/2}^{b/2}yn_{x}(x,y)\,{\text{d}}y\right){\cfrac {dw_{x}}{dx}}\,{\cfrac {d\theta _{x}}{dx}}\right.\\&\왼쪽\qquad \qquad +\lift(\int _{-b/2}^{b/2}y^{2}y^{2}n_{x}(x,y)\,{\d}y\right)\left_d\cHB\cH00\d_{dx}^{d}\riged}}$ 그리고 ${\displaystyle {\reasoned}P_{t}&=\left(\int _{-b/2}^{b/2}q_{x}(y)\,{\text{d}}y\right)w_{x}-\left(\int _{-b/2}^{b/2}m_{x}(y)\,{\text{d}}y\right){\cfrac {dw_{x}}{dx}}+\left[\int _{-b/2}^{b/2}\left(yq_{x}(y)+m_{xy}(y)\right)\,{\text{d}}y\right]\theta _{x}\\&\qquad \qquad -\left(\int _{-b/2}^{b/2}ym_{x}(y)\,{\text{d}}y\right){\cfrac {d\theta _{x}}{dx}}\,.\end{정렬}}}$ $({\displaystyle w_{}}$ x ,${\displaystyle {}_{}{}_{}}$ ${\displaystyle x_{}}$, x ${\displaystyle )}$에$$대한 $W{\displaystyle }$ ${\$$displaystyle(w_{x$},\$theta$ _${x},x)$의 첫 번째 변동을 취하여$$ 0으로 설정하면 오일러 방정식이 제공된다. ${\displaystyle {\text{(1)}}\qquad bD{\frac {\mathrm {d} ^{4}w_{x}}{\mathrm {d} x^{4}}}=q_{1}(x)-n_{1}(x){\cfrac {d^{2}w_{x}}{dx^{2}}}-{\cfrac {dn_{1}}{dx}}\,{\cfrac {dw_{x}}{dx}}-{\frac {1}{2}}{\cfrac {dn_{2}}{dx}}\,{\cfrac {d\theta _{x}}{dx}}-{\frac {n_{2}(x)}{2}}{\cfrac {d^{2}\theta _{x}}{dx^{2}}}}$ 그리고 ${\displaystyle {\text{2}}\qquad {\frac {b^{3}}D}{12}}\,{\frac {\mathrm {d} ^{4}\theta _{x}}{\mathrm {d} x^{4}}}-2bD(1-\nu ){\cfrac {d^{2}\theta _{x}}{dx^{2}}}=q_{2}(x)-n_{3}(x){\cfrac {d^{2}\theta _{x}}{dx^{2}}}-{\cfrac {dn_{3}}{dx}}\,{\cfrac {d\theta _{x}}{dx}}-{\frac {n_{2}(x)}{2}}\,{\cfrac {d^{2}w_{x}}{dx^{2}}}-{\frac {1}{2}}{\cfrac {dn_{2}}{dx}}\,{\cfrac {dw_{x}}{dx}}}$ 어디에 ${\displaystyle {\begin{aligned}q_{1}(x)&=\int _{-b/2}^{b/2}q(x,y)\,{\text{d}}y~,~~q_{2}(x)=\int _{-b/2}^{b/2}y\,q(x,y)\,{\text{d}}y~,~~n_{1}(x)=\int _{-b/2}^{b/2}n_{x}(x,y)\,{\text{d}}y\\n_{2}(x)&=\int _{-b/2}^{b/2}y\,n_{x}(x,y)\,{\text{d}}y~,~~n_{3}(x)=\int _{-b/2}^{b/2}y^{2}\,n_{x}(x,y)\,{\text{d}}y.\end{정렬}}}$ 빔이 $x{\displaystyle }$= ${\displaystyle 0}$ ${\displaystyle x=0}$에 고정되기 때문에, 우리는 다음과 같이 한다$.$ ${\displaystyle w(0,y)={\cfrac {dw}{dx}}{\Bigr }_{x=0}=0\qquad \implies \qquad w_{x}(0)={\cfrac {dw_{x}}{dx}}{\Bigr }_{x=0}=\theta _{x}(0)={\cfrac {d\theta _{x}}{dx}}{\Bigr }_{x=0}=0\,.}$ $x{\displaystyle }$= ${\displaystyle x=a}$의 경계 조건은 부품별 통합을 통해 확인할 수 있다$$. ${\displaystyle {\begin{aligned}&bD{\cfrac {d^{3}w_{x}}{dx^{3}}}+n_{1}(x){\cfrac {dw_{x}}{dx}}+n_{2}(x){\cfrac {d\theta _{x}}{dx}}+q_{x1}=0\\&{\frac {b^{3}D}{12}}{\cfrac {d^{3}\theta _{x}}{dx^{3}}}+\left[n_{3}(x)-2bD(1-\nu )\right]{\cfrac {d\theta _{x}}{dx}}+n_{2}(x){\cfrac {dw_{x}}{dx}}+t=0\\&bD{\cfrac {d^{2}w_{x}}{dx^{2}}}+m_{1}=0\quad ,\quad {\frac {b^{3}}{12}}{\cfrac {d^{2}\theta _{x}{dx^{2}}+m_{2}}}=0\end{aigned}}$ 어디에 ${\displaystyle {\begin{aligned}m_{1}&=\int _{-b/2}^{b/2}m_{x}(y)\,{\text{d}}y~,~~m_{2}=\int _{-b/2}^{b/2}y\,m_{x}(y)\,{\text{d}}y~,~~q_{x1}=\int _{-b/2}^{b/2}q_{x}(y)\,{\text{d}}y\\t&=q_{x2}+m_{3}}=\int _{-b/2}^{b/2}y\,q_{x}(y)\,{\text{d}y+\,{-b/2}^{b/2}m_{xy}(y)\,{\text{d}}y}y}y.\end{정렬}}}$

참고 항목

• 판의 휨
• 판의 진동
• 무한변형론
• 껍질 막이론
• 유한변형 이론
• 응력(기)
• 스트레스 결과물
• 선형탄성
• 벤딩
• 포플-본 카르만 방정식
• 오일러-베르누이 보 방정식
• 티모셴코 빔 이론

참조