2단계 계획 이론
Theory of two-level planning2단계 계획 이론(대안적으로, 코르나이-립탁 분해)은 선형 최적화의 큰 문제를 하위 문제로 분해하는 방법이다.이 분해는 전체적인 문제의 해결을 단순화한다.이 방법은 또한 분권화된 기업들이 글로벌 최적화를 도출하기 위해 행동하도록 경제 결정을 조정하는 방법을 모델링한다.헝가리의 경제학자 야노스 코르나이와 수학자 타마스 립타크가 1965년 도입했다.단치히의 대안이다.울프 분해.
설명
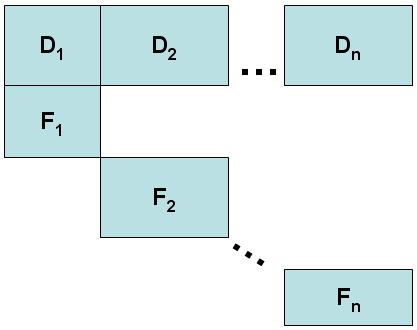
LP 문제는 블록 각도 구조로 알려진 특수한 구조를 가지고 있어야 한다.단치히 울프 분해에 필요한 구조는 다음과 같다.
중앙기획기관이 책임질 것으로 상정되는 전체 자원(D)과 개별 기업의 관심사인 계수블록(F1~Fn)에 대한 제약이 있다.
중앙 기관은 각 기업에게 전체적인 제약조건 D를 만족시키는 잠정적인 자원 배분을 제공하는 것으로 과정을 시작한다.각 기업은 글로벌 자원 배분이 그림과 같다고 가정하여 현지 의사결정 변수를 최적화한다.기업이 기획기관에 다시 전송하는 글로벌 자원에 대한 LP의 수익률 라그랑주 곱셈기(price)의 해결책.
다음 반복에서, 중앙 기관은 수정된 자원 할당을 마련하기 위해 기업으로부터 받은 정보를 사용한다. 예를 들어, 기업 I가 자원 j에 대한 높은 그림자 가격을 보고한다면, 기관은 이 자원의 더 많은 것을 이 회사에 부여하고 다른 기업에는 더 적게 제공할 것이다.수정된 잠정 배정은 개별 기업에 다시 보내지고 그 과정은 계속된다.
이 프로세스가 전체 문제에 대한 글로벌 솔루션으로 수렴(필수적으로 한정된 수는 아니지만)될 것이라는 것이 입증되었다.( 대조적으로 Dantzig Wolfe 방법은 한정된 수의 스텝으로 수렴된다.)
DW와 KL 방법은 이중적이다. DW에서는 중앙시장이 (자원에 대한 확고한 수요에 기초하여) 가격을 책정하여 그들이 요구하는 수량을 수정한 기업에 보내는 반면, KL에서는 중앙기관이 기업에 수량 정보를 보내고 기업으로부터 입찰(즉, 기업별 가격 정보)을 받는다.
참고 항목
참조
- J. Kornai, T. Liptak:2단계 계획, Econometrica, 1965년, 제33권, 페이지 141–169.[1]