sin(x)/x로 정의된 특수 수학 함수
"Sinc"는 여기서 리다이렉트 됩니다. 영국에서 야생동물이 관심 있는 지역에 대해 사용되는 명칭은 자연보존을 위한 중요 사이트(Site of Importance for Nature Conservation)를 참조하십시오. 이 기능을 기반으로 하는 신호 처리 필터는 동기 필터를 참조 하십시오. 수학 , 물리학 및 공학 에서 sinc(x ) 로 표시 되는 sinc 함수는 정규화와 비정규화의 [1]
동기 동일한 척도에 표시된 정규화 동기(파란색) 및 정규화되지 않은 동기 함수(빨간색)의 일부
일반적인 정의 동기 x = { ( 죄 x ) / x , x ≠ 0 1 , x = 0 \displaystyle \operatorname {cases}x=cases}\left(\sin x\right)/x,&x\neq 0\1,&x=0\end {cases}} 발명의 동기 전기 통신 해결일 1952 적용 분야 신호처리, 분광법 도메인 R \displaystyle \mathbb {R} 이미지 [ − 0.217234 … , 1 ] \displaystyle \left[-0.217234\ldots, 1\right] 패리티 심지어. 제로 1 + 에서의 값 0 값 - † 0 막시마 0 미니마 ± 4.49341 … {\displaystyle\pm 4.49341\ldots} 뿌리 π k , k ∈ Z ≠ 0 \displaystyle \pi k,k\in \mathbb {Z} _{\neq 0} 호혜적 { x CSC x , x ≠ 0 1 , x = 0 {\displaystyle {case}x,&x\neq 0\1,&x=0\end{case}} 파생상품 동기 ′ x = { 왜냐하면 x x − 죄 x x 2 , x ≠ 0 0 , x = 0 {\displaystyle\operatorname{cases}{\dfrac{cos x}{x^{2}},&x=0\end{cases}} 반파생적 ∫ 동기 x d x = 시 ( x ) + C {\displaystyle \int \operatorname {display} x,display=\operatorname {Si} (x)+ C} 테일러 급수 동기 x = ∑ k = 0 ∞ ( − 1 ) k x 2 k ( 2 k + 1 ) ! {\displaystyle \operatorname {displaystyle} x=\sum _{k=0}^{\infty}{\frac {\frac 1\right} ^{k}{x}{2k}}{\left(2k+1\right)! }}}
sync는 2000Hz(±1.5초 전후)에서 오디오로 기능합니다. 수학에서 과거 비정규 동기 함수 는 x 0 0에 대해
동기 x = 죄 x x . ({displaystyle\operatorname{displaystyle}x={sin x}{x}). }
또는 정규화되지 않은 sinc 함수를 샘플링 함수 (Sa(x )[2]
디지털 신호 처리 및 정보 이론 에서 정규화된 동기 함수는 일반적으로 다음과 같이 x for 0 에 대해
동기 x = 죄 ( π x ) π x . {\displaystyle \operatorname {display}x=sin(\pi x)}{\pi x}. }
두 경우 모두 x = 0 의 값은 제한값으로 정의된다.
동기 0 := 림 x → 0 죄 ( a x ) a x = 1 {\displaystyle \operatorname {display} 0:=\lim _{x\to 0}{\frac {sin(ax)}{ax}}=1} 모든 실수 a 0 0에 대해서.
정규화 로 인해 실수에 대한 함수의 확실 한 적분은 1이 됩니다(비정규화 sync 함수의 동일한 적분의 값은 θ 더욱 유용한 속성으로 정규화된 sync 함수의 0은 x 의 0이 아닌 정수 값입니다.
정규화된 동기 함수는 스케일링 없이 직사각형 함수의 푸리에 변환 입니다. 이 값은 해당 신호의 균일한 간격 의 샘플에서 연속 대역 제한 신호를 재구성 하는 개념에 사용됩니다.
두 정의 사이의 유일한 차이는 독립 변수 (x축 )의 θ 인수에 의한 스케일링입니다. 어느 경우든 0에서의 분리 가능 한 특이점에서의 함수 값은 한계치 1로 이해된다. sync 함수는 모든 곳에서 분석되므로 전체 함수가 됩니다.
sync /라는 용어 는 Philip M에 의해 도입되었습니다. 우드워드 는 1952년 "정보 이론과 통신의 역확률"이라는 글에서 이 함수가 "푸리에 분석 과 그 응용 에 너무 자주 나타나서 그것 자체의 표기법을 쓸 가치가 있는 것처럼 보인다"[3] [4] [5] 말했다 .함수 자체는 Rayleigh 경에 의해 첫 번째 종류의 0차 구형 Bessel 함수에 대한 식(Rayleigh's Formula)에서 수학적으로 처음 도출되었습니다.
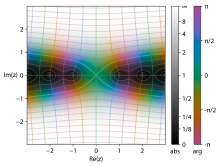
특성. 정규화되지 않은 빨간색 동기 함수의 로컬 최대값 및 최소값(작은 흰색 점)은 파란색 코사인 함수와의 교차점에 해당합니다. sinc z의 번 색소 구성).mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{.border-top:1px}고체.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}sin z/z 정규화 되지 않은 sync의 0 교차 는 θ 의 0이 아닌 정수 배수이며 정규화된 sync의 0 교차는 0이 아닌 정수에서 발생합니다.
정규화되지 않은 sync의 국소 최대값과 최소값은 코사인 함수와의 교차점에 해당합니다. 즉, sin(x )/ x θ 에 대해 sin(x )/ cos ) 이다. 따라서 이는 sync 함수의 도함수에서 파생된 것입니다.
d d x 동기 ( x ) = 왜냐하면 ( x ) − 동기 ( x ) x . {\displaystyle {frac {d}\operatorname {frac}(x)=frac {cos(x)-\operatorname {frac}(x)}{x}}. }
양 의 x 좌표를 가진 n번째 극단 x 좌표에 대한 무한 급수의 처음 몇 항은 다음과 같다.
x n = q − q − 1 − 2 3 q − 3 − 13 15 q − 5 − 146 105 q − 7 − ⋯ , {\displaystyle x_{n}=q-q^{-1}-{\frac {2}{3}-{\frac {13}{15}q^{-5}-{\frac {105}}q^{-7}-cdots}, 어디에 q = ( n + 1 2 ) π , {\displaystyle q=\left(n+{\frac {1}{2}}\right)\pi ,} 홀수 n은 로컬 최소값으로, n 은 로컬 최대값으로 이어집니다.y축 주위의 대칭 때문에 x좌표가 -x 인n 극치가 존재합니다.또한 절대 최대값은 θ 0 0, 1) 이다.
정규화된 sync 함수는 무한곱 으로 단순하게 표현됩니다.
죄 ( π x ) π x = ∏ n = 1 ∞ ( 1 − x 2 n 2 ) {\displaystyle {\frac {sin(\pi x)}{\pi x}=\display _{n=1}^{\infty}\left(1-{\frac {x^{2}}{n^{2}}\right}}} 그리고 오일러의 반사 공식을 통해 감마 함수 δ ( 죄 ( π x ) π x = 1 Γ ( 1 + x ) Γ ( 1 − x ) . (\displaystyle {\frac {\pi x}{\Gamma(1+x)\Gamma(1-x)}}). }
오일러 는 을 발견했다[6]
죄 ( x ) x = ∏ n = 1 ∞ 왜냐하면 ( x 2 n ) , ({displaystyle {\frac {sin(x)}{x}=\flac _{n=1}^{\infty}\cos \left\frac {x}{2^{n}}}\right)}) 그리고 제품 대 합의[7] ∏ n = 1 k 왜냐하면 ( x 2 n ) = 1 2 k − 1 ∑ n = 1 2 k − 1 왜냐하면 ( n − 1 / 2 2 k − 1 x ) , ∀ k ≥ 1 , \displaystyle _{n=1}^{k}\cos \left\frac {x}{2^{n}}\right)=sum _{n=1}{2^{k-1}\cos \frac {n-1/2}{2^{k-1}\light}\cos \frac {2^{k-1}\right}, 오일러의 곱은 합계로 다시 주조될 수 있다 죄 ( x ) x = 림 N → ∞ 1 N ∑ n = 1 N 왜냐하면 ( n − 1 / 2 N x ) . ({displaystyle {\frac {sin(x)}=\lim _{N\to\infty}{\frac {1}{N}}\sum _{n=1}{N}\cos \leftfrac {n-1/2}{N}x}\오른쪽). }
정규화된 동기(일반 주파수로)의 연속 푸리에 변환은 rect(f ) 입니다.
∫ − ∞ ∞ 동기 ( t ) e − i 2 π f t d t = 직교하다 ( f ) , {\displaystyle \int _{-\infty}^{\infty}\operatorname {t}(t),e^{-i2\pi ft},dt=\operatorname {rect}(f),} 여기서 직사각형 함수는 -1/ 2 / 2 이 는 동기 필터가 이상적인(직사각형 주파수 응답을 의미하는 벽돌 벽) 저역 통과 필터라는 사실에 해당합니다.
이 푸리에 적분은 특별한 경우를 포함하여
∫ − ∞ ∞ 죄 ( π x ) π x d x = 직교하다 ( 0 ) = 1 \displaystyle \int _{-\infty }^{\infty}{\frac {sin(\pi x)}{\pi x}},flac=\operatorname {rect}(0)=1} 는 부적절 한 적분(디리클레 적분 참조)이며 수렴성 르베그 적분이 아닙니다. ∫ − ∞ ∞ 죄 ( π x ) π x d x = + ∞ . \displaystyle \int _{-\infty}^{\infty}\left {\frac {sin(\pi x)}\right =+\infty}
정규화된 동기 함수에는 샘플링된 밴드 제한 함수 의 보간 과 관련하여 이상적인 특성이 있습니다.
이 는 보간 함수입니다. 즉, sinc (0) = 1 이고, 0 sinc (k ) = 0입니다.함수k x (tsinc (t k )(정수)는 함수 공간 L 2 (R )주파수 H θ (즉, 가장 높은 사이클 주파수 H = 1 /2 밴드 제한 함수에 대한 직교 정규 기준 을 형성합니다.두 sync 함수의 다른 속성은 다음과 같습니다.
비정규화된 sinc는 제1종류의 0차 구면 베셀 함수 0 (x ) 이다. 정규화된 sync는 j(µx) 입니다0 . 여기 서 Si(x ) 는 사인 적분입니다. ∫ 0 x 죄 ( θ ) θ d θ = 시 ( x ) . {\displaystyle \int _{0}^{x}{\frac {sin(\theta)}},d\theta =\operatorname {Si}(x). } γ sync ( 정규화되지 않음)는 선형 상미분 방정식에 대한 2개의 선형 독립해 중 하나이다. x d 2 y d x 2 + 2 d y d x + λ 2 x y = 0. {\displaystyle xcapfrac {d^{2}y}{display^{2}}+2capfrac {dy}{dy}+\capda ^{2}xy=0. } 다른 하나는 cos(sync )/ x 0 에서 경계가 없습니다. 정규화된 sync를 사용하여 ∫ − ∞ ∞ 죄 2 ( θ ) θ 2 d θ = π ⇒ ∫ − ∞ ∞ 동기 2 ( x ) d x = 1 , \displaystyle \int _{-\infty }^{\frac {sin ^{2}(세타)}{\theta ^{2},d\theta =\pi \pi \rightarrow \int _{-\infty }{-infty }\operatorname {{{2},x}, ∫ − ∞ ∞ 죄 ( θ ) θ d θ = ∫ − ∞ ∞ ( 죄 ( θ ) θ ) 2 d θ = π . \displaystyle \int _{-\infty }{\frac {sin(\theta)}{\theta =\int _{-\infty }{\left\frac {\sin(\theta}}}{\frac {\theta }}}{\ti}{\frac },\t},\ta =.pi. } ∫ − ∞ ∞ 죄 3 ( θ ) θ 3 d θ = 3 π 4 . {\displaystyle \int _{-\infty}^{\infty}{\frac {{3}(세타)}{\theta ^{3}},d\theta = frac {3\pi }{4}}. } ∫ − ∞ ∞ 죄 4 ( θ ) θ 4 d θ = 2 π 3 . {\displaystyle \int _{-\infty}^{\infty}{\frac {4}}{\theta ^{4}},d\theta = frac {2\pi }{3}}. } 다음 부적절한 적분에는 (정규화되지 않은) 동기 함수가 포함됩니다. ∫ 0 ∞ d x x n + 1 = 1 + 2 ∑ k = 1 ∞ ( − 1 ) k + 1 ( k n ) 2 − 1 = 1 동기 ( π n ) . {\displaystyle \int _{0}^{\infty}{\frac {x^{n}+1}=1+2\sum _{k=1}^{\infty}{\frac {(-1)^{k+1}{{{{\infty}}{\frac}{\frac}{{{{\flac}}}}{{{\flac}}}{{{{\frac}}}}}}{\frac}{\frac}}}{{{\frac}}}}}} } Dirac 델타 분포와의 관계 정규화된 동기 함수를 초기 델타 약한 한계 가 유지됨을 의미합니다.
림 a → 0 죄 ( π x a ) π x = 림 a → 0 1 a 동기 ( x a ) = δ ( x ) . \displaystyle \lim _{a\to 0}{\frac\leftx}{\pi x}}=\lim _{a\to 0}{\frac {1}{a}}\operatorname {displaystyle\frac {x}\frac {a}\frac {a}\frac {a}}=\fright}\frak {\frac}\frac}\frac}. }
왼쪽이 수렴하지 않기 때문에 이는 일반적인 한계가 아닙니다. 오히려 그 의미는
림 a → 0 ∫ − ∞ ∞ 1 a 동기 ( x a ) φ ( x ) d x = φ ( 0 ) \displaystyle \lim _{a\to 0}\int _{-\infty }^{\infty}{\operatorname {param}\leftfrac\frac {x}{a}}\right)\varphi(x),far=\varphi(0)
모든 Schwartz 함수에 대해 푸리에 반전 정리에서 볼 수 있습니다. 위의 식에서 a → 0일 때 sync 함수의 단위 길이당 발진 횟수가 무한대에 근접합니다. 단, 표현은 a의 값 에 관계없이 항상 ±1 / µx 엔벨로프 내에서 진동합니다.
이것은 θ (x ) 0 점 모든 x에 대해 0으로 복잡하게 만들고, 델타 함수를 분포가 아닌 함수로 생각하는 문제를 보여준다. 깁스 현상 에서도 비슷한 상황이 발견된다.
총계 이 섹션의 모든 합계는 정규화되지 않은 동기 함수를 나타냅니다.
1 ~ θ의 정수n 에 대한 sync(n ) 의 합은 θ 1 2
∑ n = 1 ∞ 동기 ( n ) = 동기 ( 1 ) + 동기 ( 2 ) + 동기 ( 3 ) + 동기 ( 4 ) + ⋯ = π − 1 2 . {\displaystyle \sum _{n=1}^{\infty}\operatorname {param}(n)=\operatorname {param}(1)+\operatorname {param}(3)+\cdots=fracpi-1}{pa}{param}(n})입니다. }
제곱합은 또한 θ 1 2 [8] [9]
∑ n = 1 ∞ 동기 2 ( n ) = 동기 2 ( 1 ) + 동기 2 ( 2 ) + 동기 2 ( 3 ) + 동기 2 ( 4 ) + ⋯ = π − 1 2 . {\displaystyle \sum _{n=1}^{\infty}\operatorname {filename}^{2}(n)=\operatorname {filename}^{2}(2)+\operatorname {filename}^{cd}(cd4) }
더하기 부호가 번갈아 +로 시작하는 경우 합계는 1 / 2
∑ n = 1 ∞ ( − 1 ) n + 1 동기 ( n ) = 동기 ( 1 ) − 동기 ( 2 ) + 동기 ( 3 ) − 동기 ( 4 ) + ⋯ = 1 2 . {\displaystyle \sum _{n=1}^{\infty }(-1)^{n+1},\operatorname {param}(n)=\operatorname {param}(2)+\operatorname {param}(cd1ac) {param}(frac}) }
정사각형과 정육면체의 교대로 합한 값도 1/ [10] 2
∑ n = 1 ∞ ( − 1 ) n + 1 동기 2 ( n ) = 동기 2 ( 1 ) − 동기 2 ( 2 ) + 동기 2 ( 3 ) − 동기 2 ( 4 ) + ⋯ = 1 2 , {\displaystyle \sum _{n=1}^{\infty }(-1)^{n+1},\operatorname {filename}^{2}(n)=\operatorname {filename}^{2}(2)+\operatorname {filename}{filename} {filename} {f}
∑ n = 1 ∞ ( − 1 ) n + 1 동기 3 ( n ) = 동기 3 ( 1 ) − 동기 3 ( 2 ) + 동기 3 ( 3 ) − 동기 3 ( 4 ) + ⋯ = 1 2 . {\displaystyle \sum _{n=1}^{\infty }(-1)^{n+1},\operatorname {param}^{3}(n)=\operatorname {param}^{3}(2)+\operatorname {param} ^{3}(3-operatorname} }
시리즈 확장 정규화 되지 않은 동기 함수의 Taylor 시리즈는 사인파 에서 얻을 수 있습니다.
죄 x x = ∑ n = 0 ∞ ( − 1 ) n x 2 n ( 2 n + 1 ) ! = 1 − x 2 3 ! + x 4 5 ! − x 6 7 ! + ⋯ {\displaystyle {\frac {{sin x}{x}=\sum _{n=0}^{\infty}{\frac {(-1)^{n}x^{2n}}{(2n+1)! }=1-{\frac {x^{2}}}{3! }+{\frac {x^{4}}{5! }-{\frac {x^{6}}{7! }}+\cdots }
시리즈 가 모든 x에 대해 수렴됩니다.정규화 버전은 다음과 같이 쉽게 확인할 수 있습니다.
죄 π x π x = 1 − π 2 x 2 3 ! + π 4 x 4 5 ! − π 6 x 6 7 ! + ⋯ {\displaystyle {\pi x}=1-{\pi ^{2}x^{2}}{3! }+{\frac{pi ^{4}x^{4}}{5! }-{\frac {pi ^{6}x^{6}}{7! }}+\cdots }
오일러 는 바젤 문제 를 해결하기 위해 이 시리즈를 무한곱 형태의 확장과 비교한 것으로 유명하다.
고차원 1-D 동기 함수의 곱은 사각 데카르트 그리드(예 : sinc(x , y) = sinc(y ) 에C 대한 다변량 동기 함수를 쉽게 제공합니다. sinc(y)의 푸리에 변환은 주파수 공간에서 사각형의 지시 함수(2-D 공간에 정의된 벽돌 벽)입니다. 비직교 격자 (예: 육각형 격자 )에 대한 동기 함수는 푸리에 변환이 해당 격자의 Brilouin 구역의 지시 함수인 함수 이다. 예를 들어 육각형 격자의 동기함수는 푸리에 변환이 주파수 공간에서의 단위 육각형의 지시함수인 함수 이다. 비직교 격자의 경우 이 함수는 단순한 텐서 곱으로는 구할 수 없다. 단, 육각형 , 체심입방체 , 면심입방체 및 기타 고차원 격자에 대한 동기함수의 명시적 공식은 브릴루인 구역의 기하학적 특성과 조노토프 와의 연결을 사용하여 명시적으로[11]
예를 들어, 육각형 격자는 벡터의 (정수) 선형 스팬에 의해 생성될 수 있다.
u 1 = [ 1 2 3 2 ] 그리고. u 2 = [ 1 2 − 3 2 ] . \displaystyle \mathbf {u} _{1} = param {bmatrix} {\frac {1} {2} \frac {bmatrix} \ \ faram { text { and } \ mathbf {u } _ { = param { bmatrix } \ frac } {\ frac } }
가리키다
ξ 1 = 2 3 u 1 , ξ 2 = 2 3 u 2 , ξ 3 = − 2 3 ( u 1 + u 2 ) , x = [ x y ] , {\displaystyle {\boldsymbol {xi }}_{1}=mathbf {u}_{1},\display {boldsymbol {xi }}_{2}=mathbf {u}_{2},\display {boldsymbol {xi } {3}: {u},\fr2}, {frcr},\fr}, {u}, {fr}, {{1}, {{1}, {{1}, {{1}, {1}, {1}, {{f 이 육각형 격자에 대한 동기 함수를 다음과 같이 도출할[11] 동기 H ( x ) = 1 3 ( 왜냐하면 ( π ξ 1 ⋅ x ) 동기 ( ξ 2 ⋅ x ) 동기 ( ξ 3 ⋅ x ) + 왜냐하면 ( π ξ 2 ⋅ x ) 동기 ( ξ 3 ⋅ x ) 동기 ( ξ 1 ⋅ x ) + 왜냐하면 ( π ξ 3 ⋅ x ) 동기 ( ξ 1 ⋅ x ) 동기 ( ξ 2 ⋅ x ) ) . {\displaystyle}\operatorname {text}_{\text} H}}(\mathbf {x})=big tfrac {1}{3}}{\big (}&\cos \left (\pi {boldsymbol {x}_{1}\cdot \mathbf {x} \right}\operatorname {f}\light}\cdf {\cd}\mathblight} \&{}+\cos \left(\pi {boldsymbol {x}_{2}\cdot \mathbf {x}\operatorname {right}\cdot \mathbf {x}\operatorname {xi}\cdot \leftsymboldsymbol {xi}) \\&{}+\cos \left(\pi {boldsymbol {x}_{3}\cdot \mathbf {x}\operatorname {right}\cdot \mathbf {x}\operatorname {xi}\cdot \leftsymbol {xi}) \end { aligned}}
이 구성은 일반적인 다차원 [11] Lanczos 창 을 설계하는 데 사용할 수 있습니다.
「 」를 참조해 주세요. 레퍼런스 ^ 를 클릭합니다Olver, Frank W. J. ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W., eds. (2010), "Numerical methods" , NIST Handbook of Mathematical Functions ISBN 978-0-521-19225-5 MR 2723248 ^ Singh, R. P.; Sapre, S. D. (2008). Communication Systems, 2E ISBN 978-0-07-063454-1 15페이지 발췌 ^ Woodward, P. M.; Davies, I. L. (March 1952). "Information theory and inverse probability in telecommunication" (PDF) . Proceedings of the IEE - Part III: Radio and Communication Engineering . 99 (58): 37–44. doi :10.1049/pi-3.1952.0011 . ^ Poynton, Charles A. (2003). Digital video and HDTV 147 . ISBN 978-1-55860-792-7 ^ Woodward, Phillip M. (1953). Probability and information theory, with applications to radar 29 . ISBN 978-0-89006-103-9 OCLC 488749777 . ^ Euler, Leonhard (1735). "On the sums of series of reciprocals". arXiv :math/0506415 ^ Luis Ortiz-Gracia; Cornelis W. Oosterlee (2016). "A highly efficient Shannon wavelet inverse Fourier technique for pricing European options" . SIAM J. Sci. Comput . 38 (1): B118–B143. doi :10.1137/15M1014164 . ^ "Advanced Problem 6241". American Mathematical Monthly . Washington, DC: Mathematical Association of America . 87 (6): 496–498. June–July 1980. doi :10.1080/00029890.1980.11995075 . ^ Robert Baillie; David Borwein ; Jonathan M. Borwein (December 2008). "Surprising Sinc Sums and Integrals". American Mathematical Monthly . 115 (10): 888–901. doi :10.1080/00029890.2008.11920606 . hdl :1959.13/940062 JSTOR 27642636 . S2CID 496934 . ^ Baillie, Robert (2008). "Fun with Fourier series". arXiv :0806.0150v2 math.CA ]. ^ a b c Ye, W.; Entezari, A. (June 2012). "A Geometric Construction of Multivariate Sinc Functions". IEEE Transactions on Image Processing . 21 (6): 2969–2979. Bibcode :2012ITIP...21.2969Y . doi :10.1109/TIP.2011.2162421 . PMID 21775264 . S2CID 15313688 . 외부 링크 



![{\displaystyle \left[-0.217234\ldots ,1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/601b4e66864e716d3744d8deadaaed1ec6ad1032)









































