축삭계

반원형 아치 통로의 더 큰 돌출부입니다.

축삭계는 3차원 물체의 평면 이미지를 생성하는 기술 기하학에 속하는 그래픽 절차입니다."축도 측정"이란 "축을 따라 측정하는 것"을 의미하며 좌표축의 치수와 축척이 중요한 역할을 한다는 것을 나타낸다.축삭 측정 절차의 결과는 물체의 균일한 축척 평행 투영입니다.일반적으로 평행 투영 결과는 비스듬하지만(레이가 영상 평면에 수직이 아님), 특별한 경우 결과는 직교 축삭측정법이라고 하는 직교 축삭측정법입니다.

테크니컬 드로잉과 건축에서 축색 투시법은 3차원 물체의 2차원 표현 형태이며, 부피 또는 부피의 인상을 보존하는 것이 목표입니다.때로는 빠른 원근법 또는 인공 원근법이라고도 불리며, 원뿔 원근법과는 다르며 실제로 눈으로 보는 것을 나타내지 않는다: 특히 평행선은 평행하게 유지되고 멀리 있는 물체의 크기는 줄어들지 않는다.중심이 무한대로 밀려난 원뿔 원뿔 원뿔 원뿔 원뿔로 간주할 수 있다. 즉, 관찰된 물체에서 매우 멀리 떨어져 있다.

축삭계라는 용어는 아래에 설명된 그래픽 절차와 이 절차에서 생성된 영상 모두에 사용됩니다.

축삭측정법은 영국 문헌에서 직교 축삭측정법을 지칭하는 축삭측정법과 혼동해서는 안 된다.

축삭 측정 원리

P ¯

¯ （ {

displaystyle

{ P

{\overline {P}}

} ）

P=(x,y,z)

(

P=(x,y,z)

,

P=(x,y,z)

, z

P=(x,y,z)

) {

displaystyle

P = (

x

,

y

, z ) }의

{\overline {P}}

P=(x,y,z)

투영 평면 π the the 。앞줄기는 v

v_{x}

{

display style

v _ {

x

、

v_{y}

\

display

style

v

_ {

y

} 、

v_{z}

z \

display style

v _ {

z

} 입니다

v_y

.

Pohlke의 정리는 ^[1]^[2]3차원 물체의 축척 평행 투영을 구성하기 위한 다음 절차의 기초입니다.

세 개의 좌표 축이 모두 단일 점 또는 선으로 축소되지 않도록 좌표 축의 투영을 선택합니다.일반적으로 z축은 수직입니다.
이러한 투영을 위해 $v_{x}$ x $v_{x}$ { $displaystyle$ $v_{$ $x$ $v_{y}$ { $y}$ 및 $v_{y}$ $v_{z}$ z {\ $displaystyle v_{z$ 를 $v_{x}$ 합니다. $v_{x},v_{y},v_{z}>0.$ 서 v x $v_{x},v_{y},v_{z}>0.$ $v_{x},v_{y},v_{z}>0.$ $v_{x},v_{y},v_{z}>0.$ $v_{x},v_{y},v_{z}>0.$ z > $.$ { $displaystyle v_{x}, v_{z}$ > $0.$ $}$
$P=(x,y,z)$ P $P=(x,y,z)$ ( $P=(x,y,z)$ , $P=(x,y,z)$ , $P=(x,y,z)$ ) {{ display ${\overline {P}}$ $style$ ${\overline {P}}$ P = ( $x$ , y , z ) }의 ${\overline {P}}$ P $¯$ { $display$ $style$ { P ${\overline {P}}$ } ( x , y , $z$ )는 ${\overline {P}}$ $P=(x,y,z)$ 세 가지 하위 단계로 결정됩니다(결과는 하위 단계의 순서와 무관합니다).
- $({$ $display$ ${\overline {O}}$ style ${O$ 에서 시작하여 $v_{x}\cdot x$ $({$ $display$ ${\overline {x}}$ style $v_$ ${x$ ${\overline {x}}$ $cdot$ x}) ${\overline {x}}$ 으로 $v_x\cdot x$ $v_{x}\cdot x$ 합니다.
- $y$ $v_{y}\cdot y$ 으로 $v_{y}\cdot y$ y ${\overline {y}}$ y y y $v_{y}\cdot y$ \ $display$ v $_$ { $y$ $}$ \ $cdot$ y만큼 $이동$ 합니다 $v_y\cdot y$ .
- $v$ $v_{z}\cdot z$ $v_{z}\cdot z$ {\ $v_{z}\cdot z$ z { $style$ v_ ${z}\$ $cdot$ z } $만큼$ z ${\overline {z}}$ by 방향으로 이동한 후 마지막으로
마지막 위치를 ${\overline {P}}$ P로 표시합니다 $({$

왜곡되지 않은 결과를 얻으려면 축의 투영과 단축을 신중하게 선택하십시오(아래 참조).직각 투영을 생성하기 위해 좌표 축의 투영만 자유롭게 선택되며, 전단은 고정됩니다(de:orthogonale Axonometrie ^[3]참조).

축 및 단축의 영상 선택

파라미터 및 표기

표기법:

$\alpha :$ $:$ ${\overline {x}}$ 과 ${\overline {z}}$ ${\overline {x}}$ x축 ${\overline {x}}$ 의 ${\overline {x}}$ ${\overline {z}}$ (\ $displaystyle\alpha$ $:\$ displaystyle $\alpha :$ $\$ displaystyle ${x})$
$\beta :$ : $\beta :$ z축과 ${\overline {z}}$ ${\overline {y}}$ y축 ${\overline {y}}$ 의 ${\overline {y}}$ 각도 $(\$ displaystyle\displaystyle ${z$
$\gamma :$ ${\overline {y}}$ : $x축$ 과 $\gamma :$ y축 ${\overline {x}}$ 의 $각도$ $: {\$ $displaystyle\$ displaystyle\ $displaystyle$ $\$ displaystyle ${\overline {x}}$ \displaystyle $\gamma :$ ${\overline {y}}$ {y $}}$

각도는 0 $0^{\circ }<\alpha +\beta <360^{\circ }\ .$ < $0^{\circ }<\alpha +\beta <360^{\circ }\ .$ $0^{\circ }<\alpha +\beta <360^{\circ }\ .$ β < $0^{\circ }<\alpha +\beta <360^{\circ }\ .$ {\ $displaystyle$ 0 $^{\circ$ }<\ $alpha +\beta$ < $360^{\circ }\.}$ 이 $0^{\circ }<\alpha +\beta <360^{\circ }\ .$ 선택할 수 있습니다.
$0<\;v_{x},\;v_{y},\;v_{z}\ .$ $0<\;v_{x},\;v_{y},\;v_{z}\ .$ < $0<\;v_{x},\;v_{y},\;v_{z}\ .$ x , $0<\;v_{x},\;v_{y},\;v_{z}\ .$ $0<\;v_{x},\;v_{y},\;v_{z}\ .$ , $0<\;v_{x},\;v_{y},\;v_{z}\ .$ z $0<\;v_{x},\;v_{y},\;v_{z}\ .$ . { $displaystyle$ 0 < \ ; v $_$ { $x$ , \ ; $v$ _ { $y$ , \ ; $v$ _ { z $0<\;v_{x},\;v_{y},\;v_{z}\ .$ } \ $0<\;v_{x},\;v_{y},\;v_{z}\ .$ }

각도 및 단축을 적절하게 선택하는 경우에만 왜곡되지 않은 영상을 얻을 수 있습니다.다음 다이어그램은 다양한 각도 및 단축에 대한 단위 큐브의 이미지를 보여 주며 이러한 개인 선택을 하는 방법에 대한 몇 가지 힌트를 제공합니다.

단위 큐브의 다양한 축삭 이미지.(이미지 평면이 y-z 평면에 평행합니다.)
왼쪽과 오른쪽 끝의 이미지는 큐브가 아니라 긴 큐보이드처럼 보입니다.

체크무늬 용지에 주택의 축색계(캐버럴 원근법)를 적용.

도면을 단순하게 유지하려면 1. $(\displaystyle$ 1. $0)$ $또는$ 0.5(\ $displaystyle$ 0.5 $0.5$ 와 $1.0$ 같이 단순 단축을 선택해야 합니다.

두 단락이 같으면 투영을 치수 측정이라고 합니다.
세 개의 단락이 같으면 투영을 등각도라고 합니다.
모든 단축이 다른 경우 투영을 트리메트릭이라고 합니다.

오른쪽 다이어그램(예: 그래프 용지에 그려진 집의)의 매개 변수는 α $\alpha =135^{\circ },\beta =90^{\circ },\ v_{y}=v_{z}=1,\;v_{x}=1/{\sqrt {2}}\ .$ $\alpha =135^{\circ },\beta =90^{\circ },\ v_{y}=v_{z}=1,\;v_{x}=1/{\sqrt {2}}\ .$ , β $\alpha =135^{\circ },\beta =90^{\circ },\ v_{y}=v_{z}=1,\;v_{x}=1/{\sqrt {2}}\ .$ $\alpha =135^{\circ },\beta =90^{\circ },\ v_{y}=v_{z}=1,\;v_{x}=1/{\sqrt {2}}\ .$ µ, $\alpha =135^{\circ },\beta =90^{\circ },\ v_{y}=v_{z}=1,\;v_{x}=1/{\sqrt {2}}\ .$ $\alpha =135^{\circ },\beta =90^{\circ },\ v_{y}=v_{z}=1,\;v_{x}=1/{\sqrt {2}}\ .$ $\alpha =135^{\circ },\beta =90^{\circ },\ v_{y}=v_{z}=1,\;v_{x}=1/{\sqrt {2}}\ .$ $\alpha =135^{\circ },\beta =90^{\circ },\ v_{y}=v_{z}=1,\;v_{x}=1/{\sqrt {2}}\ .$ $\alpha =135^{\circ },\beta =90^{\circ },\ v_{y}=v_{z}=1,\;v_{x}=1/{\sqrt {2}}\ .$ 1, $\alpha =135^{\circ },\beta =90^{\circ },\ v_{y}=v_{z}=1,\;v_{x}=1/{\sqrt {2}}\ .$ $\alpha =135^{\circ },\beta =90^{\circ },\ v_{y}=v_{z}=1,\;v_{x}=1/{\sqrt {2}}\ .$ $\alpha =135^{\circ },\beta =90^{\circ },\ v_{y}=v_{z}=1,\;v_{x}=1/{\sqrt {2}}\ .$ / $\alpha =135^{\circ },\beta =90^{\circ },\ v_{y}=v_{z}=1,\;v_{x}=1/{\sqrt {2}}\ .$ 입니다 $.$ \ $displaystyle$ \ $alpha$ = $135$ ^{\ $display },$ \ $display$ = $90 = {\y} v_v$ {1},이미지 평면이 y-z 평면에 평행하고 y-z 평면에 평행한 평면 도형이 실제 모양으로 나타납니다.

특수 축색계

변환된 좌표 축 사이의 각도(α, β, θ), 수평선으로부터의 각도(α_h, β_h, β_h 미포함 = 90°)를 가진 일반적으로 사용되는 투영 및 원근법

이름 또는 속성	α = δx470z	β = βγz	"="x""	α_h	β_h	V_x	V_y	V_z	v
직교, 직교, 평면	90°	0°	270°	0°	270°	v		0%	조금도
트리메트릭	90° +α_h	90° + β_h	360° − α − β	조금도	조금도	조금도	조금도	조금도	조금도
치수 측정						조금도	v
등각선						v
보통의						v			100%
경사, 임상 촬영				90° 미만	90° 미만	조금도	조금도	조금도	황갈색(α_h)
대칭		α	360° − 2·α	90° 미만	α_h				조금도
등각선	120°			30°					조금도
정상, 1:1 등각도						v			100%
표준, 단축 등각선									${\textstyle {\sqrt {\frac {2}{3}}}}$ 3 ( $텍스트$ 스타일 $){$ frac { ${\textstyle {\sqrt {\frac {2}{3}}}}$ $frac$ { $2$ } 81
픽셀, 1:2 등각도	116.6°		126.9°	아크탄(v)					50%
공학 기술	131.4°	97.2°	131.4°	아크(3/4)	arcsin(1/8)	50%	v		100%
카발리어	90° +α_h	90°	270° − α	조금도	0°	조금도
캐비닛, 치수 측정 캐벌리어	90° +α_h		270° − α	조금도		100% 미만
표준 등각 캐벌리어	135°		135°	45°		v
표준 1:2 캐비닛	135°		135°	45°		50%	v
30° 캐비닛	116.6°		153.4°	아크탄_x(v)
60° 캐비닛	153.4°		116.6°	아크코드(v_x)
30° 캐벌리어	120°		150°	30°		조금도
공중, 조감도	135°		90°	45°		v		조금도	100%
군사의	135°			45°		v			100%
평면 측정	90° +α_h	180° − α_h		조금도	90° − α_h				조금도
표준 평탄도계									100%
평면도 측정 단축									2/3 67 67 %

특수 축삭 측정의 매개 변수입니다.

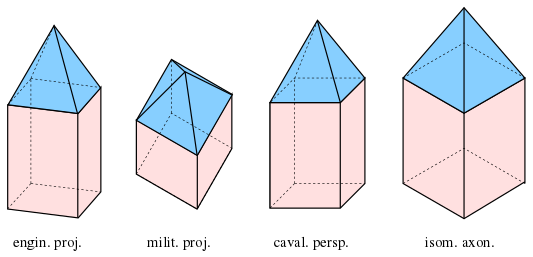
엔지니어 투영

이 경우

단, 다음과 $v_{x}=0.5,\ v_{y}=v_{z}=1\$ . $v_{x}=0.5,\ v_{y}=v_{z}=1\$ x $v_{x}=0.5,\ v_{y}=v_{z}=1\$ $v_{x}=0.5,\ v_{y}=v_{z}=1\$ $v_{x}=0.5,\ v_{y}=v_{z}=1\$ y $v_{x}=0.5,\ v_{y}=v_{z}=1\$ $v_{x}=0.5,\ v_{y}=v_{z}=1\$ $v_{x}=0.5,\ v_{y}=v_{z}=1\$ $v_{x}=0.5,\ v_{y}=v_{z}=1\$ { $displaystyle v_{x$ } = $v_{x}=0.5,\ v_{y}=v_{z}=1\$ 0.5 $,\ v_{y$ } = $v_{z$ } = $1\ }$ (차원 축삭계)
$\alpha =132^{\circ },\ \beta =97^{\circ }\ .$ 사이의 각도는 α $\alpha =132^{\circ },\ \beta =97^{\circ }\ .$ $\alpha =132^{\circ },\ \beta =97^{\circ }\ .$ , β $\alpha =132^{\circ },\ \beta =97^{\circ }\ .$ $\alpha =132^{\circ },\ \beta =97^{\circ }\ .$ θ $\alpha =132^{\circ },\ \beta =97^{\circ }\ .$ {\ $displaystyle$ \ $alpha$ = $\alpha =132^{\circ },\ \beta =97^{\circ }\ .$ θ^{\display $},$ \displaystyle $= 97^{\display$ } \ $\alpha =132^{\circ },\ \beta =97^{\circ }\ .$ } 입니다.

이러한 각도는 많은 독일어 집합 정사각형에 표시됩니다.

엔지니어 예측의 장점:

단순 단축,
스케일링 계수 1.06을 사용하여 균일하게 스케일링된 맞춤 투영,
구의 윤곽선은 원(일반적으로 타원)입니다.

상세한 것에 대하여는, 「de:」를 참조해 주세요.액소노메트리.

캐벌리어 관점, 캐비닛 관점

이미지 평면을 y-z 평면에 평행하게 만듭니다.

문헌에서 "캐비탈 관점"과 "캐비닛 관점"이라는 용어는 균일하게 정의되어 있지 않다.위의 정의가 가장 일반적인 정의입니다.많은 경우 추가 제한이 적용됩니다.^[6]^[7]예를 들어 다음과 같습니다.

캐비닛의 관점: 추가로

α

\alpha =135^{\circ }

135

\alpha =135^{\circ }

=

135

= 135 =

135^{\

displaystyle

\alpha =135^{\circ }

}}

\alpha =135^{\circ }

(각선) 및

v_{x}=0.5

x

v_{x}=0.5

0.

v_{x}=0.5

({

x} =

0.

5

（ 치수)를

\alpha =135^{\circ }

합니다.

캐벌리어 관점: 추가로

\alpha =135^{\circ }

\alpha =135^{\circ }

135

\alpha =135^{\circ }

(\

displaystyle

\

alpha

= 135

^{\display

})

\alpha =135^{\circ }

v_{x}=1

v

v_{x}=1

=

(\

displaystyle v_{x

}=1}

(

등각도)를

\alpha =135^{\circ }

합니다.

조감도, 군사 투영

x-y 평면에 평행한 이미지 평면

군사 투영: 추가로 v

v_{z}=1

=

(\displaystyle v_{z

}=

1}(

등각도)을

v_{z}=1

합니다.

이러한 축색계는 수평 도형을 왜곡되지 않게 하기 위해 도시 지도에 자주 사용된다.

등각 축삭계

표준등각: 입방체, 입방체, 집 및 구

(미터 공간 간의 등각도와 혼동하지 마십시오.)

등각 축삭계의 경우 모든 단축이 동일하다.각도는 임의로 선택할 수 있지만, 일반적인 선택은 $\alpha =\beta =\gamma =120^{\circ }$ $\alpha =\beta =\gamma =120^{\circ }$ β $\alpha =\beta =\gamma =120^{\circ }$ $\alpha =\beta =\gamma =120^{\circ }$ $\alpha =\beta =\gamma =120^{\circ }$ $\alpha =\beta =\gamma =120^{\circ }$ µ { $display$ \ $alpha$ = \ $display$ = \display = $120^{\display$ 이다.

표준 등각도 또는 등각도만을 위해 다음을 선택한다.

$v_{x}=v_{y}=v_{z}=1$ x $v_{x}=v_{y}=v_{z}=1$ $v_{x}=v_{y}=v_{z}=1$ y $v_{x}=v_{y}=v_{z}=1$ $v_{x}=v_{y}=v_{z}=1$ $v_{x}=v_{y}=v_{z}=1$ $= 1$ { $displaystyle$ v $_$ { x } = $v_{x}=v_{y}=v_{z}=1$ v _ { y } = $v$ _ { z } $=$ 1 (모든 축이 변형되지 않음)
$\displaystyle \alpha =\displays = 120^{\displays }\ .}$

표준 등각계의 장점은 다음과 같습니다.

좌표를 변경하지 않고 취할 수 있습니다.
이미지는 스케일 ${\sqrt {1.5}}=1.225$ 1.5 $=$ 1 $(\displaystyle\displaystyle\displaystyle\{$ 1.5}= $1.$ display ${\sqrt {1.5}}=1.225$ 의 축척된 맞춤법 투영입니다. 따라서 이미지는 인상이 좋고 구의 윤곽은 원입니다.
일부 컴퓨터 그래픽 시스템(xfig 등)은 적절한 래스터(그림 참조)를 지원합니다.

스케일링을 방지하기 위해 쇼트닝을 핸디하게 선택할 수 있습니다.

$v_{x}=v_{y}=v_{z}={\sqrt {2/3}}$ x $v_{x}=v_{y}=v_{z}={\sqrt {2/3}}$ $v_{x}=v_{y}=v_{z}={\sqrt {2/3}}$ y $v_{x}=v_{y}=v_{z}={\sqrt {2/3}}$ $v_{x}=v_{y}=v_{z}={\sqrt {2/3}}$ z $v_{x}=v_{y}=v_{z}={\sqrt {2/3}}$ / $v_{x}=v_{y}=v_{z}={\sqrt {2/3}}$ { $displaystyle v$ _ { x } = $v$ _ { y } = $v_$ { z } = $scarrt { 2$ / $3$ } $v_{x}=v_{y}=v_{z}={\sqrt {2/3}}$ （ 1 ）

이미지는 (축소된) 맞춤법 투영입니다.

탑의 여러 축삭계

v_{z}=0.5,v_{x,y}=1

측정 군사 투영:

v_{z}=0.5,v_{x,y}=1

v_{z}=0.5,v_{x,y}=1

v_{z}=0.5,v_{x,y}=1

0.

v_{z}=0.5,v_{x,y}=1

x

v_{z}=0.5,v_{x,y}=1

v_{z}=0.5,v_{x,y}=1

=

v_{z}=0.5,v_{x,y}=1

{\displaystyle v_{z

}= 0.5

,

v_{x}=0.5,v_{y,z}=1

{x,y

}=

1

치수 측정 공학 및 캐벌리어 투영:

v_{x}=0.5,v_{y,z}=1

x

v_{x}=0.5,v_{y,z}=1

0.

v_{x}=0.5,v_{y,z}=1

v_{x}=0.5,v_{y,z}=1

,

v_{x}=0.5,v_{y,z}=1

1

{

displaystyle v_{x

}

=

0.5

,v_yz

},

v_{x}=0.5,v_{y,z}=1

axonometometricalometry:1,

축삭측정법에서의 원

원의 평행한 돌기는 일반적으로 타원형이다.원의 평면이 이미지 평면에 평행하면 원의 이미지가 일치하는 원이 되는 중요한 특수한 경우가 발생합니다.그림에서 전면에 포함되는 원은 일그러지지 않는다.원의 화상이 타원일 경우 직교 직경 및 접선 주변의 정사각형에 4개의 점을 매핑할 수 있으며, 화상 평행사변형에서는 손으로 타원을 채운다.시간이 많이 걸리는 더 좋은 방법은 원의 두 수직 직경의 이미지를 그리는 것입니다.원 직경은 이미지 타원의 공역 직경이며, Ryz의 구조에 따라 타원의 축을 결정하고 타원을 그리는 것입니다.

대승적 관점: 동그라미
군사 투영: 구체

축삭측정법에서의 구

구의 일반적인 축삭측정법에서 영상 윤곽선은 타원형입니다.구의 윤곽선은 직교 축삭측정법에서만 원입니다.그러나 엔지니어 투영과 표준 등각도는 스케일링된 직각 투영이므로 구체의 윤곽도 원입니다.그림과 같이 구체의 윤곽으로서의 타원은 혼란스러울 수 있으므로 구체가 매핑할 물체의 일부인 경우 직교 축삭측정법 또는 엔지니어 투영법 또는 표준 등각법을 선택해야 합니다.

레퍼런스

Graf, Ulrich; Barner, Martin (1961). Darstellende Geometrie. Heidelberg: Quelle & Meyer. ISBN 3-494-00488-9.
Fucke, Kirch Nickel (1998). Darstellende Geometrie. Leipzig: Fachbuch-Verlag. ISBN 3-446-00778-4.
Leopold, Cornelie (2005). Geometrische Grundlagen der Architekturdarstellung. Stuttgart: Kohlhammer Verlag. ISBN 3-17-018489-X.
Brailov, Aleksandr Yurievich (2016). Engineering Graphics: Theoretical Foundations of Engineering Geometry for Design. Springer. ISBN 978-3-319-29717-0.
Stärk, Roland (1978). Darstellende Geometrie. Schöningh. ISBN 3-506-37443-5.

메모들

^ Graf 1961, 페이지 144
^ 세인트크 1978, 페이지 156
^ Graf 1961, 페이지 145
^ Graf 1961, 페이지 155
^ Stérk 1978, 페이지 168
^ Graf 1961, 95페이지
^ 세인트크 1978, 페이지 159

외부 링크

직교 축삭계

[FOOTNOTEGraf1961144-1] Graf 1961, 페이지 144

[FOOTNOTEStärk1978156-2] 세인트크 1978, 페이지 156

[FOOTNOTEGraf1961145-3] Graf 1961, 페이지 145

[FOOTNOTEGraf1961155-4] Graf 1961, 페이지 155

[FOOTNOTEStärk1978168-5] Stérk 1978, 페이지 168

[FOOTNOTEGraf196195-6] Graf 1961, 95페이지

[FOOTNOTEStärk1978159-7] 세인트크 1978, 페이지 159

[1]

[2]

[3]

[6]

[7]

v t 기술 정보의 시각화
필드	생체 데이터 시각화 화학 이미징 범죄 매핑 데이터 시각화 교육용 시각화 흐름 시각화 지구 가시화 정보 시각화 수학적 시각화 의료 영상 분자 그래픽스 제품 시각화 과학적 시각화 소프트웨어 시각화 기술 도면 사용자 인터페이스 설계 시각 문화 볼륨 시각화
이미지 타입	차트 도표 엔지니어링 도면 함수의 그래프 표의문자 지도 사진 픽토그램 줄거리. Sankey 다이어그램 개략도 골격식 통계 그래픽스 테이블 기술 도면 테크니컬 일러스트
사람	자크 베르탱 신시아 브루어 스튜어트 카드 실라 카펜데일 토마스 A.드판티 보든 덴트 마이클 프렌들리 조지 퍼나스 팻 한라한 나이젤 홈스 크리스토퍼 R. 존슨 고든 킨들만 아우구스트 케쿨레 마누엘 리마 앨런 맥에어런 잭 D. 매킨레이 마이클 말츠 브루스 매코믹 미리아 마이어 찰스 조셉 미너드 루돌프 모들리 가스파르 몽게 타마라 먼즈너 오토 뉴라스 플로렌스 나이팅게일 한스페터 피스터 클리포드 A.픽오버 캐서린 프라이산트 윌리엄 플레이페어 카를 빌헬름 폴케 아돌프 케테레 조지 G. 로버트슨 아서 H. 로빈슨 로렌스 J. 로젠블럼 벤 쉬나이더맨 클라우디오 실바 프레이저 스토다트 에드워드 터프테 페르난다 비가스 아데 올루페코 하워드 웨이너 마틴 바텐버그 방왕 마우로 마르티노 모리츠 스테파너
관련 토픽	지도 제작 차트정크 컴퓨터 그래픽스 컴퓨터 공학에서 CPK 착색 그래프 그리기 그래픽 디자인 그래픽 오거나이저 영상과학 정보 그래픽스 정보과학 잘못된 그래프 신경 영상 촬영 특허 도면 과학적 모델링 공간 분석 시각 분석 시각 지각 볼륨 지도 제작 볼륨 렌더링 인포메뉴

Search

축삭계

네임스페이스

더

목차

축삭 측정 원리

축 및 단축의 영상 선택

특수 축색계

엔지니어 투영

캐벌리어 관점, 캐비닛 관점

조감도, 군사 투영

등각 축삭계

축삭측정법에서의 원

축삭측정법에서의 구

레퍼런스

외부 링크