중력에 대한 기계적 설명

중력에 대한 기계적 설명(또는 중력의 운동 이론)은 먼 거리에서의 어떠한 작용도 사용하지 않고 밀어서 생기는 압력과 같은 기본적인 기계적 과정을 통해 중력의 작용을 설명하려는 시도입니다.이 이론들은 에테르와 관련하여 16세기부터 19세기까지 발전되었다.하지만, 그러한 모형은 더 이상 주류 과학계에서 실행 가능한 이론으로 간주되지 않으며, 일반 상대성이론은 이제 멀리 있는 행동을 사용하지 않고 중력을 묘사하는 표준 모형이다.현대의 "양자 중력" 가설은 또한 입자장과 같은 보다 근본적인 과정을 통해 중력을 설명하려고 시도하지만, 그것들은 고전 역학에 기초하지 않습니다.

스크리닝

이 이론은 아마도 가장 잘 알려진 기계적 설명일 것이고^[1], 1690년 니콜라 파티오 드 뒤리에에 의해 처음으로 개발되었고, 특히 조르주 루이 르 세이지(1748), 켈빈 경(1872), 헨드리크 로렌츠(1900)에 의해 다시 발명되었고, 제임스 서기 포와 맥스웰(1875)에 의해 비판되었다.

이 이론은 중력의 힘이 우주의 모든 방향에서 빠른 속도로 움직이는 작은 입자 또는 파도의 결과라고 가정합니다.입자의 플럭스의 세기는 모든 방향에서 동일하다고 가정하기 때문에 고립된 물체 A는 모든 측면에서 균등하게 부딪혀서 내향의 압력만 생기고 순방향의 힘은 발생하지 않는다.그러나 두 번째 물체 B가 존재하면 A에 B의 방향에서 부딪혔을 입자의 일부가 가로채기 때문에 B는 차폐 역할을 한다. 즉, B의 방향에서 보면 A는 반대 방향에서 부딪히는 입자의 수가 줄어든다.마찬가지로, B는 A의 방향에서 맞은 입자의 수가 반대 방향에서 맞은 입자의 수보다 적을 것이다.A와 B는 서로 그림자를 드리우고 있으며, 그 결과 힘의 불균형에 의해 두 물체는 서로 밀리고 있다고 말할 수 있다.

이 그림자는 반제곱 법칙을 따릅니다.왜냐하면 물체를 둘러싼 구면 전체의 운동량 흐름의 불균형은 둘러싸인 구면의 크기와 무관하지만 구면의 표면적은 반지름의 제곱에 비례하여 증가하기 때문입니다.질량 비례성의 필요성을 충족시키기 위해, 이론은 a) 물질의 기본 원소가 매우 작아서 총 물질이 대부분 빈 공간으로 구성되고 b) 입자가 너무 작아서 그 중 극히 일부만 총 물질에 의해 가로채는 것으로 가정한다.그 결과, 각 물체의 "그림자"는 물질의 모든 원소의 표면에 비례합니다.

비판:이 이론은 입자나 파동이 적어도 부분적으로 흡수될 때만 그림자가 이 모델에 나타나기 때문에 주로 열역학적인 이유로 거절되었고, 이는 신체에 엄청난 열을 가할 것이다.또한 드래그, 즉 운동 방향의 입자 흐름의 저항도 큰 문제입니다.이 문제는 초광속도로 해결할 수 있지만, 이 해법은 열 문제를 크게 증가시키고 특수 상대성 이론과 ^[2][3]모순된다.

소용돌이 이론

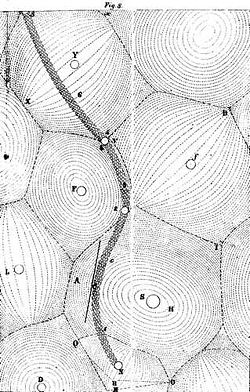
그의 철학적인 믿음 때문에, 르네 데카르트는 1644년에 빈 공간은 존재할 수 없으며 결과적으로 공간은 물질로 채워져야 한다고 제안했다.이 물질의 부분들은 직선 경로로 움직이는 경향이 있지만, 서로 가까이 있기 때문에 자유롭게 움직일 수 없으며, 데카르트에 따르면 모든 움직임은 원형이기 때문에 에테르에 소용돌이로 채워진다고 합니다.데카르트는 또한 거친 물질이 미세 물질보다 더 강하게 원형 운동에 저항하는 물질의 다른 형태와 크기를 구별합니다.원심력으로 인해 물질은 소용돌이의 바깥 가장자리를 향해 이동하고, 거기서 이 물질의 응결을 일으킨다.거친 물질은 더 큰 관성으로 인해 이 움직임을 따라갈 수 없습니다. 따라서 응축된 외부 물질의 압력으로 인해 이러한 부분이 소용돌이의 중심으로 밀려납니다.데카르트에 따르면, 이 내부 압력은 중력일 뿐이다.그는 이 메커니즘을 회전하는 액체를 채운 용기가 멈추면 액체가 계속 회전한다는 사실과 비교했다.이제, 만약 누군가가 작은 물체 조각들(예: 나무)을 용기 안으로 떨어뜨리면, 그 조각들은 용기 ^[4][5][6]중앙으로 이동한다.

데카르트의 기본 전제조건에 따라, 1669년과 1690년 사이의 Christiaan Huygens는 훨씬 더 정확한 소용돌이 모형을 설계했다.이 모델은 수학적으로 도출된 최초의 중력 이론이었다.그는 에테르 입자가 모든 방향으로 움직인다고 가정했지만 소용돌이의 바깥쪽 경계에서 다시 던져졌고, 이것이 (데카르트의 경우처럼) 바깥쪽 경계에서 미세 물질의 농도를 증가시켰다.그래서 그의 모형에서도 미세 물질이 거친 물질을 소용돌이의 중심으로 밀어넣습니다.호이겐스는 또한 원심력이 소용돌이의 중심(구심력) 방향으로 작용하는 힘과 같다는 것을 알아냈다.그는 또한 에테르가 체내에 쉽게 침투할 수 있도록 몸은 대부분 빈 공간으로 구성되어야 하며, 이는 질량 비례성에 필요하다고 가정했다.그는 또한 에테르가 낙하하는 물체보다 훨씬 더 빨리 움직인다고 결론지었다.이때 뉴턴은 끌어당김에 기초한 중력 이론을 개발했고 호이겐스는 수학적 형식론에 동의했지만 힘의 법칙에 대한 기계적 설명이 부족하기 때문에 모형은 불충분하다고 말했다.중력이 역제곱 법칙에 따른다는 뉴턴의 발견은 호이겐스를 놀라게 했고 그는 에테르 속도가 ^[6][7][8]더 멀리 떨어져 있다고 가정함으로써 이것을 고려하려고 했다.

비판:아이작 뉴턴은 항력이 ^[9]관찰되지 않은 궤도의 현저한 편차로 이어져야 하기 때문에 그 이론에 반대했다.또 다른 문제는 위성이 종종 소용돌이 운동의 방향과 반대되는 다른 방향으로 움직인다는 것이었다.그는 프린키피아 매스매티카 제2권의 대부분을 데카르테 소용돌이 이론의 반박에 할애하고 있다.또한, 역제곱 법칙에 대한 호이겐스의 설명은 원형인데, 이는 에테르가 케플러의 제3법칙을 따른다는 것을 의미하기 때문이다.하지만 중력 이론은 그 법칙들을 설명해야 하고 그것들을 ^[6][9]전제해서는 안 된다.

몇몇 영국 물리학자들은 19세기 후반에 소용돌이 원자 이론을 발전시켰다.그러나 물리학자 윌리엄 톰슨, 켈빈 남작은 상당히 다른 접근법을 개발했다.데카르트는 각각 빛의 방출, 투과 및 반사에 관련된 세 가지 물질의 종류를 설명했지만, 톰슨은 단일 ^[10]연속체에 기초한 이론을 개발했습니다.

데카르트 소용돌이 이론은 코페르니쿠스의 태양 중심 이론과 태양과 같은 여러 개의 별이 존재하고,^[11] 그 주위를 도는 여러 개의 행성으로 둘러싸인 우주에 대한 믿음에서 중요한 역할을 했다.

스트림

헨리 올덴버그에게, 그리고 나중에 로버트 보일에게 보낸 1675년 편지에서, 뉴턴은 다음과 같이 썼다: "중력은 흐름의 속도 증가와 관련된 에테르 밀도의 그에 상응하는 얇음과 함께 에테르의 흐름을 일으키는 응축의 결과이다."그는 또한 그러한 과정이 그의 다른 모든 연구와 케플러의 ^[12]운동 법칙과 일치한다고 주장했다.흐름 속도 증가와 관련된 뉴턴의 압력 강하 아이디어는 1738년 다니엘 베르누이의 책 하이드로다이나미카에서 발표된 베르누이의 원리로 수학적으로 공식화되었습니다.

하지만, 그는 나중에 두 번째 설명을 제안했지만(아래 섹션 참조), 그 질문에 대한 뉴턴의 언급은 여전히 모호했다.1692년 벤틀리에게 보낸 세 번째 편지에는 다음과 같이 ^[13]썼다.

에피쿠로스의 의미에서의 중력이 필수적이고 내재되어 있는 경우처럼, 무생물 물질이 물질적이지 않은 다른 무언가의 매개 없이 상호 접촉 없이 다른 문제에 작용하고 영향을 미친다는 것은 상상할 수 없다.그리고 이것이 당신이 '중력'을 내 탓으로 돌리지 않기를 바라는 이유 중 하나입니다.중력은 선천적이고 본질적이며 물질에 필수적이어야 한다. 그래야 한 몸이 먼 곳에서, 진공 상태를 통해, 다른 어떤 것에 대한 조정 없이, 그들의 행동과 힘이 서로 간에 전달될 수 있는 것은 나에게 너무나 큰 불합리이다. 그래서 나는 철학적 문제를 가진 사람은 없다고 믿는다.생각의 원동력은 절대 빠질 수 없다.중력은 특정 법칙에 따라 끊임없이 행동하는 에이전트에 의해 야기되어야 합니다. 그러나 이 에이전트가 물질적이든 중요하지 않든 저는 독자들의 고려에 맡겼습니다.

한편, 뉴턴은 또한 1713년에 ^[14]쓰여진 논핑거 가설로 잘 알려져 있다.

나는 현상에서 이러한 중력의 성질에 대한 이유를 아직 발견하지 못했고 가설을 가장하지도 않는다.현상으로부터 추론되지 않은 것은 모두 가설이라고 불려야 합니다; 그리고 가설은 형이상학적 혹은 물리적인, 또는 신비적 성질에 기초하든, 또는 기계적인지에 근거하든, 실험 철학에서 설 자리가 없습니다.이 철학에서 특정 명제는 현상으로부터 추론되며, 이후 귀납에 의해 일반화된다.

그리고 니콜라스 파티오 드 뒤리에나 데이비드 그레고리 같은 그의 친구들의 증언에 따르면, 뉴턴은 중력은 신의 ^[8]영향을 직접적으로 기반으로 한다고 생각했다.

뉴턴과 비슷하지만 수학적으로 더 상세하게, 베른하르트 리만은 1853년에 중력 에테르가 압축할 수 없는 유체이며 정상 물질은 이 에테르의 흡수원을 나타낸다고 가정했습니다.따라서 에테르가 체내의 질량에 비례하여 파괴되거나 흡수되면, 흐름이 일어나 모든 주변 물체를 중심 질량 방향으로 운반합니다.리만은 흡수된 에테르를 다른 세계나 ^[15]차원으로 옮긴다고 추측했다.

에너지 문제를 해결하기 위한 또 다른 시도는 1888년 이반 오시포비치 야르코프스키에 의해 이루어졌다.그는 리만과 비슷한 에테르류 모델을 바탕으로 흡수된 에테르류가 새로운 물질로 변환되어 ^[16]천체의 대량 증가를 초래할 수 있다고 주장했다.

비판:르세지의 이론처럼 아무런 설명 없이 에너지가 사라지는 것은 에너지 절약 법칙에 위배된다.또한 약간의 저항이 발생해야 하며 물질의 생성으로 이어지는 어떠한 과정도 알려져 있지 않습니다.

정압

뉴턴은 광학(1717) 제2판을 또 다른 기계-에테르 중력 이론으로 업데이트했다.그의 첫 번째 설명(1675 - 스트림 참조)과는 달리, 그는 천체 근처에서 점점 얇아지는 고정 에테르를 제안했다.양력의 비유로, 힘이 생겨 모든 물체를 중심 질량에 밀어 넣습니다.그는 중력 에테르의 밀도가 매우 낮다고 말함으로써 항력을 최소화했다.

뉴턴처럼, 레온하르트 오일러는 1760년에 중력 에테르가 역제곱 법칙에 따라 밀도를 잃는다고 가정했다.다른 사람들과 비슷하게, 오일러는 또한 질량비례성을 유지하기 위해 물질은 대부분 ^[17]빈 공간으로 이루어져 있다고 가정했다.

비판:뉴턴과 오일러 둘 다 정적 에테르의 밀도가 변해야 하는 이유를 제시하지 않았다.게다가, 제임스 클럭 맥스웰은 이 "정압" 모델에서 "스트레스의 상태... 우리가 투명 매체 안에 존재해야 하는 것은 가장 강한 강철이 지탱할 수 있는 것보다 3000배나 큽니다."^[18]

흔든다

로버트 후크는 1671년에 중력은 모든 물체가 에테르를 통해 모든 방향으로 파장을 방출하는 결과라고 추측했다.이러한 파도와 상호작용하는 다른 물체는 파동의 근원 방향으로 움직인다.후크는 교란된 수면 위의 작은 물체들이 ^[19]교란의 중심으로 이동한다는 사실을 유추했다.

비슷한 이론이 제임스 챌린리스에 의해 1859년부터 1876년까지 수학적으로 제시되었다.그는 중력체 간 거리에 비해 파장이 크면 인력의 경우가 발생한다고 계산했다.파장이 작으면 물체는 서로 밀어낸다.이러한 효과들의 조합으로, 그는 또한 다른 모든 ^[20]힘들을 설명하려고 노력했다.

비판:맥스웰은 이 이론이 파동의 지속적인 생산을 필요로 하며,^[21] 이는 무한한 에너지 소비를 수반해야 한다고 반대했다.Challis 본인은 과정이 ^[19]복잡하기 때문에 확실한 결과에 이르지 못했다고 인정했습니다.

맥동

켈빈 경(1871)과 칼 안톤 비어크네스(1871)는 모든 물체가 에테르에서 맥동한다고 가정했다.이것은 유체에서 두 구의 맥박이 같으면 서로 끌어당기고, 두 구의 맥박이 같지 않으면 서로 밀어낸다는 사실과 유사했다.이 메커니즘은 전하의 성질을 설명하는 데도 사용되었다.무엇보다도, 이 가설은 조지 가브리엘 스톡스와 월드마르 보이트에 ^[22]의해서도 검토되었다.

비판: 만유인력을 설명하기 위해, 사람들은 우주의 모든 맥동이 같은 위상이라고 가정하도록 강요당한다. 이것은 매우 불가능해 보인다.또한 에테르를 압축할 수 없는 상태로 유지하여 흡인력이 더 ^[22]먼 거리에서도 발생하도록 해야 합니다.그리고 맥스웰은 이 과정이 영구적인 새로운 ^[18]에테르 생산과 파괴를 수반해야 한다고 주장했다.

기타 이력 투기

1690년, 피에르 바리뇽은 모든 물체는 모든 방향에서 에테르 입자에 의해 밀리는 것에 노출되며, 지구 표면으로부터 일정한 거리에서는 입자가 통과할 수 없는 어떤 제한이 있다고 가정했다.그는 만약 물체가 한계 경계보다 지구에 더 가까이 있다면, 그 물체는 아래보다 위로부터 더 큰 힘을 받아 ^[23]지구로 떨어지게 될 것이라고 추정했다.

1748년, 미하일 로모노소프는 에테르 효과가 물질 구성 요소의 전체 표면과 비례한다고 가정했다(그의 앞의 호이겐스와 파티오와 유사).그는 또한 시체들의 엄청난 침투성을 가정했다.그러나 에테르와 물질이 어떻게 상호작용하여 만유인력의 ^[24]법칙이 일어나는지에 대해서는 명확한 설명이 없었다.

1821년, 존 헤라패스는 그가 개발한 기체 운동 이론 모델을 중력에 적용하려고 시도했다.그는 에테르가 물체에 의해 가열되고 밀도가 낮아져 다른 물체가 더 낮은 ^[25]밀도의 영역으로 밀려난다고 가정했다.그러나 Taylor는 열팽창에 의한 밀도 저하가 가열입자의 속도 증가로 보상되므로 흡인력이 ^[19]발생하지 않는다는 것을 보여주었다.

최근의 이론화

중력에 대한 이러한 기계적 설명은 널리 받아들여지지 않았지만, 비록 그러한 생각들은 20세기 초까지 물리학자들에 의해 종종 연구되었고, 그 때쯤에는 그것이 일반적으로 신뢰받지 못하는 것으로 여겨졌습니다.하지만, 과학의 주류 밖에 있는 일부 연구자들은 여전히 그 이론들의 결과들을 알아내려고 노력합니다.

르 세이지의 이론은 ^[26]라지예프스키와 카갈니코바,^[27] 슈나이데로프,^[28] 부오노마노와 엥겔스,^[29] 아다무트,^[30] 자크콜라,^[31] 톰 반 플랑데른, 에드워즈 등에 의해 연구되었다.^[32]Edwards ^[33]등에서는 다양한 Le Sage 모델과 관련 주제에 대해 설명합니다.

정압에 의한 중력은 최근 Arminjon에 ^[34]의해 연구되었다.

레퍼런스

원천