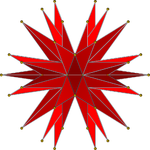
이코사면체 최종면도
Final stellation of the icosahedron기하학에서, 이도사면체의[1][2] 완전 또는 최종의 절개는 이도사면체의 가장 바깥쪽 절개이며, 이도사면체의 절개도에 모든 세포가 포함되기 때문에 "완전"하고 "최종"이다. 즉, 고드름 중심부의 교차하는 세 면마다 이 다면체의 꼭지점이나 그 안쪽에 교차한다.
이 다면체는 이코사면체의 17번째 단면이며, Wenninger 모델 지수 42로 주어진다.
기하학적 수치로서 아래에 기술된 두 가지 해석이 있다.
- 20개의 동일한 자가 교차 에네그램 면, 90개의 가장자리, 60개의 정점을 가진 불규칙 별(자체 교차) 다면체로서.
- 삼각형 면 180개(이소셀 60개, 스칼렌 120개), 가장자리 270개, 꼭지점 92개를 가진 단순한 다면체로서. 이 해석은 다면체 모형 건축에 유용하다.
요하네스 케플러는 1619년 정규 항성 폴리헤드라(케플러-푸인소트 다면체)를 만드는 기형을 연구했지만, 불규칙한 얼굴을 가진 완전한 이코사면체는 맥스 브뤼크너에 의해 1900년에 처음 연구되었다.
역사
 브뤼크너 모델 (Taf. XI, 그림 14, 1900)[3] |
 에치드나 |
- 1619: 하모니스 먼디에서 요하네스 케플러는 먼저 스텔화 과정을 적용하여 작은 스텔화 도데카드론과 큰 스텔화 도데카드론을 일반 다면체로 인식하였다.[4]
- 1809:루이스 푸인소트가 케플러의 다면체를 재발견했고, 두 가지 더, 지금은 케플러-푸인소 다면체라 불리는 일반 별 다면체로서의 위대한 이코사면체와 위대한 도데면체를 발견했다.[5]
- 1812: 아우구스틴루이 카우치는 항성 다면체(polyedra)[6]를 추가로 열거하여, 일반 다면체(polyedra)가 4개뿐임을 증명했다.
- 1900: Max Bruckner는 스텔레이션 이론을 정규 형태를 넘어 확장시켰고, 완전한 스텔레이션을 포함한 10개의 스텔링을 확인했다.[3]
- 1924: A.H. Wheeler는 1924년에 완전한 스텔링을 포함한 20개의 스텔레이션 양식 목록(반사본 포함 22개)을 발표했다.[7]
- 1938: 1938년 저서 The Fifth Nine Icosaedra, H. S. M. Coxeter, P.에서. Du Val, H. T. Flater, J. F. Petrie는 일반 이코사면체에 대한 일련의 스텔링 규칙을 명시했고 그 규칙들에 부합하는 59개의 스텔링에 대한 체계적인 조사를 했다. 이 책의 제8권이라고 할 수 있다.
- 1974: Wenninger의 1974년 저서 Polyhedron Models에서, 이코사헤드론의 최종 스텔링은 지수 W를42 가진 스텔링 이코사헤드라의 17번째 모델로 포함되어 있다.
- 1995: Andrew Hume은 그의 Netlib 다면체 데이터베이스에서 그것을 echidnahedron[8](에치드나, 또는 가시가 있는 개미핥기는 거친 털과 가시로 덮여 있고 스스로를 보호하기 위해 공 모양으로 구부러지는 작은 포유동물이다.)이라고 이름지었다.
해석
기장으로서.
다면체의 스텔링은 다면체의 얼굴을 무한 면으로 확장하고, 면으로서 이 면들에 의해 경계되는 새로운 다면체를 생성하며, 가장자리로서 이 면들의 교차점을 생성한다. 이코사헤드라는 J. C. P. 밀러가 제시한 규칙 집합에 따라 일반 이코사헤드론(The Fifth Nine Icosaheedra)의 묘사를 열거하고 있으며, 여기에는 완전한 묘사가 포함된다. 완전한 스텔레이션의 두발 기호는 H인데, 가장 바깥쪽 "h" 층까지 스텔레이션 다이어그램에 있는 모든 셀을 포함하기 때문이다.[6]
단순 다면체로서
 다면 모델은 12개의 면 세트로 구성될 수 있으며, 각각 5개의 피라미드 그룹으로 접혀 있다. |
단순하고 가시적인 표면 다면체로서 최종면체의 외부 형태는 180개의 삼각면으로 구성되어 있는데, 이는면체 도표에서 가장 바깥쪽 삼각면이다. 이들은 270개의 가장자리를 따라 결합하며, 이는 92개의 꼭지점에서 만나며 오일러 특성은 2이다.[9]
92개의 꼭지점이 세 개의 동심원 구 표면에 놓여 있다. 가장 안쪽의 20개의 꼭지점은 일반 도두면체의 정점을 형성하고, 다음 층인 12는 일반 이두면체의 정점을 형성하며, 바깥 층인 60은 불균일하게 잘린 이두면체의 정점을 형성한다. 이 구들의 반경은 비율에[10] 있다.
가장자리 길이 a, φa, φa2 및 φa2√2(여기서는 φ이 황금비)를 가진 3차원 고체 물체로 간주될 때, 완전한 이코사면체는 표면적을[10] 가진다.
부피와 부피[10]
별다면체로서
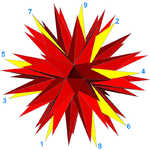 스무살 9⁄4 폴리곤 면(한 면은 노란색이고 9개의 꼭지점이 표시되어 있음) | 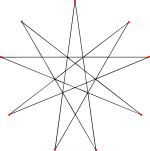 2-등각9⁄4 면 |
완전한 석면은 밑단 이코사면체의 20면에 해당하는 20개의 얼굴을 가진 자기 교차 별 다면체로도 볼 수 있다. 각각의 얼굴은 불규칙한 9/4 별 다각형 또는 에네그램이다.[6] 세 개의 면이 각 꼭지점에서 만나기 때문에 20 × 9 / 3 = 60 꼭지점(이것은 가시 정점의 가장 바깥 층이며 "스핀"의 끝을 형성한다)과 20 × 9 / 2 = 90 가장자리(별 다면체의 각 가장자리는 180개의 가시 가장자리 중 두 개를 포함하며 연결한다).
항성 이코사면체로 간주될 때 완전한 석면은 고귀한 다면체인데, 이는 등면체(얼굴-변환)와 이소각체(Vertex-변환)이기 때문이다.
참고 항목
메모들
- ^ Coxeter 외 연구진(1938), 페이지 30~31
- ^ Wenninger, 다면체 모델, 페이지 65.
- ^ Jump up to: a b 브뤼크너, 맥스(1900)
- ^ Weisstein, Eric W. "Kepler-Poinsot Solid". MathWorld.
- ^ Louis Poinsot, Memoire sur les polygones et polyédres. 루이 푸인소트 J. de L'école 폴리테크니크 9 페이지 16–48, 1810.
- ^ Jump up to: a b c 크롬웰(1999년) (p. 259)
- ^ 휠러(1924년)
- ^ echidnahedron이라는 이름은 netlibpolyheadron 데이터베이스의 개발자인 Andrew Hume에게 인정될 수 있다.
"... 그리고 에치드나헤드론(내 이름, 그것이 실제로 이코사헤드론의 마지막 점막이다.)을 포함한 몇몇 이상한 고형물도 있다."지오메트리. 리서치; "폴리헤드라 데이터베이스"; 1995년 8월 30일 오전 12시.
- ^ Echidnahedron 2008-10-07년 Wayback Machine(polyhedra.org)에 보관
- ^ Jump up to: a b c Weisstein, Eric W. "Echidnahedron". MathWorld.
참조
- 브뤼크너, 맥스(1900년) Vielecke und Vielflache: 테오리와 게시히테 라이프치히: B.G. 트레브너. ISBN 978-1-4181-6590-1. (독일어) WorldCat English: Polygons 및 Polyedra: 이론과 역사. 모델 사진: 타펠 8세(플레이트 8세) 등 하이 레즈 스캔.
- A. H. Wheeler, 특정 형태의 이코사면체 및 상위 다면체를 도출하고 지정하는 방법, Proc. 인터내타트. 수학. 의회, 1924년 토론토, 1권 701-708
- H.S.M. Coxeter, 일반 폴리토페스, (3판, 1973년), 도버판, ISBN 0-486-61480-8, 3.6 6.2 플라토닉 고형물 스텔링, 페이지 96–104
- Coxeter, Harold Scott MacDonald; Du Val, P.; Flather, H. T.; Petrie, J. F. (1999), The fifty-nine icosahedra (3rd ed.), Tarquin, ISBN 978-1-899618-32-3, MR 0676126 (제1회 Edn University of Toronto (1938년)
- Wenninger, Magnus J, Polyhedron 모델; 케임브리지 대학 출판부, 제1대 Edn(1983년), Ppbk(2003년). ISBN 978-0-521-09859-5. (모델 42, 페이지 65, 아이코사체 최종면도)
- Cromwell, Peter R. (1997). Polyhedra. Cambridge University Press. ISBN 0-521-66405-5.
- 젠킨스, 제럴드, 막달렌 베어. Icosaheadron의 최종 묘지: 잘라내고 접착하는 고급 수학 모델. 영국 노퍽주: 타킨 출판사, 1985년 ISBN 978-0-906212-48-6
외부 링크
- Ralph Jones에 의한 Echidnaheadron(.doc) 모델 구성 지침 포함
- 이코사면체(Idosaheadron)를 찌르고 Guy Inchbald에 의해 도데카면체(Dodecaheadron)를 표면화하는 방향으로
- Weisstein, Eric W. "Fifty nine icosahedron stellations". MathWorld.
- 이코사면체의 기단
- 이코사헤드론 59기
- VRML 모델: http://www.georgehart.com/virtual-polyhedra/vrml/echidnahedron.wrl
- Netlib: 다면체 데이터베이스, 모델 141
| 이코사면체의 눈에 띄는 흔적 | |||||||||
| 정규 | 균일 듀얼 | 정규 화합물 | 항성 | 다른이들 | |||||
| (콘벡스) 이코사면체 | 작은삼각형 이코사면체 | 중삼면체 | 대삼면체 | 5옥타헤드라 화합물 | 5개의 사면체 화합물 | 사면체 10개 화합물 | 대이코사면체 | 발굴된 도데면체 | 파이널 스텔레이션 |
|---|---|---|---|---|---|---|---|---|---|
 |  |  |  |  |  |  |  |  | |
 |  |  |  |  |  |  |  |  | |
| 이코사헤드론에서의 스텔레이션 과정은 많은 관련 다면체와 이코사면 대칭을 가진 화합물을 생성한다. | |||||||||