대략적인 문자열 일치
Approximate string matching컴퓨터 과학에서 대략적인 문자열 매칭(흔히 퍼지 문자열 검색이라고 함)은 대략 (정확한 것이 아니라) 패턴과 일치하는 문자열을 찾는 기술이다.대략적인 문자열 매칭 문제는 일반적으로 주어진 문자열 내에서 대략적인 하위 문자열 일치를 찾는 것과 패턴과 근사적으로 일치하는 사전 문자열을 찾는 두 가지 하위 문제로 나뉜다.
개요
성냥의 폐쇄성은 문자열을 정확한 성냥으로 변환하는 데 필요한 원시적 연산의 수로 측정한다.이 숫자를 문자열과 패턴 사이의 편집 거리라고 한다.일반적인 원시 운영은 다음과 같다.[1]
- 삽입: cot → coat
- 삭제: 코트 → cot
- 대체: 코트 → 비용
이 세 가지 연산은 문자가 삭제되거나 삽입되는 곳마다 NULL 문자(여기서는 *로 상징됨)를 추가하여 대체의 형태로 일반화될 수 있다.
- 삽입: co*t → coat
- 삭제: 코트 → co*t
- 대체: 코트 → 비용
어떤 근사치들은 또한 문자열에서 두 글자의 위치가 바뀌는 전위치를 원시적인 수술로 취급하기도 한다.[2]
- 전환: 비용 → 요트
근사치 행렬이 다르면 제약조건이 다르다.일부 계산자는 단일 글로벌 비가중 비용, 즉 일치 항목을 패턴으로 변환하는 데 필요한 총 원시 작업 수를 사용한다.예를 들어, 패턴이 코일인 경우 호일은 대체 1개, 코일은 삽입 1개, 오일은 삭제 1개, 포일은 대체 2개로 차이가 난다.모든 작업이 단일 비용 단위로 계산되고 한도가 1로 설정되면 포일, 코일 및 오일은 일치로 계산되지만 포울은 그렇지 않다.
다른 계산자는 각 유형의 작업 수를 별도로 지정하지만, 다른 계산자는 총 비용을 설정하지만 다른 가중치를 다른 작업에 할당하도록 허용한다.일부 계산자는 패턴의 개별 그룹에 제한과 가중치를 별도로 할당하는 것을 허용한다.
문제 제식 및 알고리즘
대략적인 문자열 일치 문제에 대한 가능한 정의는 다음과 같다: 패턴 P = 2. . . . . and a text string , find a substring in T, which, of all substrings of T, has the smallest edit distance to the pattern P.
Brute-force 접근방식은 T의 모든 서브스트링에 대해 P에 대한 편집 거리를 계산한 다음 최소 거리로 하위 문자열을 선택하는 것이다.그러나 이 알고리즘은 실행 시간 O(n3 m)을 가질 것이다.
셀러가[3] 제안한 더 나은 솔루션은 동적 프로그래밍에 의존한다.문제의 대안적 공식화를 사용한다: 텍스트 T의 각 위치 j와 패턴 P의 각 위치 i에 대해, 패턴의 i 첫 번째 문자, 와 위치 j에서 끝나는 T의 하위 문자열 사이의 최소 편집 거리를 계산한다.
텍스트 T의 각 위치 j와 패턴 P의 각 위치 i에 대해, 위치 j에서 끝나는 T의 모든 하위 문자열을 거치고, 패턴 P의 i 첫 문자에 대한 최소 편집 거리를 가진 문자 중 하나를 결정한다.이 최소 거리를 E(i, j)로 쓰시오.모든 i와 j에 대해 E(i, j)를 계산한 후, 우리는 쉽게 원래의 문제에 대한 해결책을 찾을 수 있다: 그것은 E(m, j)가 최소인 하위 문자열이다(패턴 P의 길이).
컴퓨팅 E(m, j)는 두 문자열 사이의 편집 거리를 계산하는 것과 매우 유사하다.실제로 E(m, j)에 대해 레벤슈틴 거리 계산 알고리즘을 사용할 수 있는데, 유일한 차이점은 0으로 첫 번째 행을 초기화해야 한다는 점, 즉 E(i - 1,j), E(i,j - 1) 또는 E(i - 1,j - 1)를 컴퓨팅 E(i, j)에 사용했는지의 여부다.
E(x, y) 값이 들어 있는 배열에서 마지막 행의 최소값을 선택하고 E(x2, y2)가 되도록 한 다음 0행까지 계산 경로를 역행한다.우리가 도착한 필드가 E(0, y)라면 T[y11 + 1]...T[y2]는 패턴 P에 대한 편집 거리가 최소인 T의 하위 문자열이다.
E(x, y) 어레이를 계산하려면 동적 프로그래밍 알고리즘으로 O(mn) 시간이 걸리는 반면 역작동 단계는 O(n + m) 시간이 걸린다.
또 다른 최근의 아이디어는 유사성 결합이다.데이터베이스를 일치시키는 것이 대량의 데이터와 관련되는 경우, 동적 프로그래밍 알고리즘을 사용한 O(mn) 시간은 제한된 시간 내에 작동할 수 없다.그래서 모든 문자열 쌍의 유사성을 계산하는 대신 후보 쌍의 수를 줄이자는 생각이다.널리 사용되는 알고리즘은 필터 검증, 해싱, 로컬리티 민감 해싱(LSH), 시도 및 기타 욕심 많고 근사 알고리즘에 기초한다.이들 대부분은 동시에 계산하는 데 일부 프레임워크(예: 지도-리듀스)에 맞도록 설계되어 있다.
온라인 대 오프라인
전통적으로 대략적인 문자열 매칭 알고리즘은 온라인과 오프라인이라는 두 가지 범주로 분류된다.온라인 알고리즘을 사용하면 검색하기 전에 패턴을 처리할 수 있지만 텍스트는 처리할 수 없다.즉, 온라인 기법은 색인 없이 검색을 한다.온라인 대략적인 일치를 위한 초기 알고리즘은 바그너와 피셔 그리고[4] 셀러스에[5] 의해 제안되었다.두 알고리즘 모두 동적 프로그래밍을 기반으로 하지만 서로 다른 문제를 해결한다.바그너와 피셔의 알고리즘이 사전 퍼지 검색에만 적합하게 레벤쉬틴 거리를 계산하는 동안 셀러의 알고리즘은 텍스트에서 대략적으로 하위 문자열을 검색한다.
온라인 검색 기술이 거듭 개선됐다.아마도 가장 유명한 개선은 비교적 짧은 패턴 문자열에 매우 효율적인 비트맵 알고리즘(또는 시프트와 시프트 앤드 알고리즘이라고도 한다)일 것이다.Bitap 알고리즘은 Unix 검색 유틸리티 agrep의 핵심이다.온라인 검색 알고리즘에 대한 검토는 지 나바로가 했다.[6]
비록 매우 빠른 온라인 기법이 존재하지만, 대용량 데이터에 대한 그들의 성능은 받아들일 수 없다.텍스트 사전 처리 또는 인덱싱을 통해 검색 속도 대폭 향상오늘날 다양한 인덱싱 알고리즘이 제시되었다.그 중에는 접미사 나무[7], 미터법 나무[8], n그램 방법 등이 있다.[9][10]텍스트에서 임의의 하위 문자열을 찾을 수 있는 인덱싱 기법의 상세한 조사는 나바로 외 연구원이 제공한다.[11]사전 방법(즉, 검색 패턴과 거의 일치하는 모든 사전 단어 찾기를 허용하는 방법)에 대한 컴퓨터 조사는 보이트소프가[12] 제공한다.
적용들
대략 일치되는 일반적인 적용은 철자 검사를 포함한다.[13]대량의 DNA 데이터가 사용 가능해지면서 뉴클레오티드 시퀀스의 매칭은 중요한 적용 분야가 되었다.[14]스팸 필터링에도 대략적인 일치가 사용된다.[15]레코드 연계는 서로 다른 두 데이터베이스의 레코드가 일치하는 공통 응용 프로그램이다.
문자열 일치는 이미지와 음악과 같은 대부분의 이진 데이터에는 사용할 수 없다.음향 지문 인식과 같은 다른 알고리즘이 필요하다.
참고 항목
참조
- ^ Baeza-Yates, R.; Navarro, G. (June 1996). "A faster algorithm for approximate string matching". In Dan Hirchsberg; Gene Myers (eds.). Combinatorial Pattern Matching (CPM'96), LNCS 1075. Irvine, CA. pp. 1–23. CiteSeerX 10.1.1.42.1593.
- ^ Baeza-Yates, R.; Navarro, G. "Fast Approximate String Matching in a Dictionary" (PDF). Proc. SPIRE'98. IEEE CS Press. pp. 14–22.
- ^ Boytsov, Leonid (2011). "Indexing methods for approximate dictionary searching: Comparative analysis". Journal of Experimental Algorithmics. 16 (1): 1–91. doi:10.1145/1963190.1963191. S2CID 15635688.
- ^ Cormen, Thomas; Leiserson, Rivest (2001). Introduction to Algorithms (2nd ed.). MIT Press. pp. 364–7. ISBN 978-0-262-03293-3.
- ^ Galil, Zvi; Apostolico, Alberto (1997). Pattern matching algorithms. Oxford [Oxfordshire]: Oxford University Press. ISBN 978-0-19-511367-9.
- ^ Gusfield, Dan (1997). Algorithms on strings, trees, and sequences: computer science and computational biology. Cambridge, UK: Cambridge University Press. ISBN 978-0-521-58519-4.
- ^ Myers, G. (May 1999). "A fast bit-vector algorithm for approximate string matching based on dynamic programming" (PDF). Journal of the ACM. 46 (3): 395–415. doi:10.1145/316542.316550. S2CID 1158099.
- Navarro, Gonzalo (2001). "A guided tour to approximate string matching". ACM Computing Surveys. 33 (1): 31–88. CiteSeerX 10.1.1.96.7225. doi:10.1145/375360.375365. S2CID 207551224.
- ^ Navarro, Gonzalo; Baeza-Yates, Ricardo; Sutinen, Erkki; Tarhio, Jorma (2001). "Indexing Methods for Approximate String Matching" (PDF). IEEE Data Engineering Bulletin. 24 (4): 19–27.
- ^ Sellers, Peter H. (1980). "The Theory and Computation of Evolutionary Distances: Pattern Recognition". Journal of Algorithms. 1 (4): 359–73. doi:10.1016/0196-6774(80)90016-4.
- ^ Skiena, Steve (1998). Algorithm Design Manual (1st ed.). Springer. ISBN 978-0-387-94860-7.
- ^ Ukkonen, E. (1985). "Algorithms for approximate string matching". Information and Control. 64 (1–3): 100–18. doi:10.1016/S0019-9958(85)80046-2.
- ^ Wagner, R.; Fischer, M. (1974). "The string-to-string correction problem". Journal of the ACM. 21: 168–73. doi:10.1145/321796.321811. S2CID 13381535.
- ^ Zobel, Justin; Dart, Philip (1995). "Finding approximate matches in large lexicons". Software: Practice and Experience. 25 (3): 331–345. CiteSeerX 10.1.1.14.3856. doi:10.1002/spe.4380250307. S2CID 6776819.
외부 링크
- 플라밍고 프로젝트
- 편집 거리 임계값을 기반으로 한 대략적인 문자열 일치가 최근 진보한 효율적인 유사성 쿼리 처리 프로젝트.
- StringMetric 프로젝트 String 메트릭스 및 음성 알고리즘의 Scala 라이브러리
- 일반적인 문자열 메트릭 구현을 포함하는 JavaScript 자연 언어 처리 라이브러리 자연 프로젝트
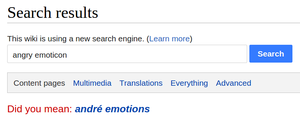




 하위 문자열
하위 문자열