Listen to this article

시퀀스 정렬

Sequence alignment

생물정보학에서 시퀀스 정렬은 DNA, RNA 또는 단백질의 시퀀스를 배열하여 시퀀스 사이의 기능적, 구조적 또는 진화적 관계의 결과일 수 있는 유사성 영역을 식별하는 방법이다.[1]뉴클레오티드 또는 아미노산 잔류물의 정렬된 순서는 일반적으로 행렬 내에서 행으로 표현된다.동일하거나 유사한 문자가 연속된 열에 정렬되도록 잔여물 사이에 간격을 삽입한다.시퀀스 정렬은 자연어 또는 재무 데이터에서 문자열 사이의 거리 비용을 계산하는 것과 같은 비생물학적 시퀀스에도 사용된다.

ClustalO가 포유류 히스톤 단백질의 시퀀스 정렬.
염기서열은 단백질의 잔류물 120-180을 위한 아미노산이다.모든 시퀀스에 보존된 잔여물은 회색으로 강조 표시된다.단백질 순서 아래에는 보존 순서(*), 보수적 돌연변이(:), 반보수적 돌연변이(.) 및 비보수적 돌연변이( ).[2]

해석

정렬에서 두 시퀀스가 공통 조상을 공유하는 경우 불일치는 점 돌연변이와 간격(즉, 삽입 또는 삭제 돌연변이)으로 해석될 수 있다.단백질의 순서 정렬에서, 아미노산이 배열에서 특정 위치를 차지하는 유사성의 정도는 특정 부위나 염기서열 모티브가 선 사이에 얼마나 보존되어 있는지를 대략적으로 보여주는 척도로 해석할 수 있다.시퀀스의 특정 영역에서 대체물이 없거나 매우 보수적인 대체물(즉, 사이드 체인이 유사한 생화학적 특성을 갖는 아미노산의 대체물)만 존재한다는 것은 이 지역이 구조적 또는 기능적 중요성을 가지고 있음을 시사한다.DNA와 RNA 뉴클레오티드 베이스는 아미노산보다 서로 유사하지만 염기쌍의 보존은 유사한 기능적 또는 구조적 역할을 나타낼 수 있다.

정렬 방법

매우 짧거나 매우 유사한 시퀀스는 손으로 정렬할 수 있다.그러나, 대부분의 흥미로운 문제들은 인간의 노력만으로 정렬될 수 없는 길고, 매우 가변적이거나 극도로 많은 시퀀스의 정렬을 요구한다.그 대신 알고리즘을 구성하여 고품질 시퀀스 정렬을 만들고, 알고리즘적으로 표현하기 어려운 패턴(특히 뉴클레오티드 시퀀스의 경우)을 반영하도록 최종 결과를 조정하는 데 인간의 지식이 적용되기도 한다.시퀀스 정렬에 대한 계산적 접근방식은 일반적으로 글로벌 정렬과 로컬 정렬의 두 가지 범주로 나뉜다.전역 정렬 계산은 정렬을 모든 쿼리 시퀀스의 전체 길이에 걸쳐 "강제"하는 글로벌 최적화의 한 형태다.대조적으로, 국소 선형은 종종 전체적으로 크게 다른 긴 시퀀스 내에서 유사성의 영역을 식별한다.국부적 정렬이 선호되는 경우가 많지만 유사 영역을 식별해야 하는 추가적인 어려움 때문에 계산하기가 더 어려울 수 있다.[4]시퀀스 정렬 문제에 다양한 연산 알고리즘이 적용되었다.여기에는 동적 프로그래밍과 같이 느리지만 공식적으로 올바른 방법이 포함된다.이러한 방법에는 또한 대규모 데이터베이스 검색을 위해 설계된 효율적이고 경험적인 알고리즘 또는 확률론적인 방법들이 포함되며, 이러한 방법들은 최상의 일치점을 찾는 것을 보장하지 않는다.

표현

선형은 일반적으로 그래픽으로 표현되고 텍스트 형식으로 표현된다.거의 모든 시퀀스 정렬 표현에서 정렬된 잔여물이 연속적인 열에 나타나도록 배열된 행으로 시퀀스를 기록한다.텍스트 형식에서, 동일하거나 유사한 문자를 포함하는 정렬된 열은 보존 기호 시스템과 함께 표시된다.위의 이미지에서와 같이, 별표나 파이프 기호는 두 열 사이의 정체성을 나타내기 위해 사용된다; 다른 덜 일반적인 기호는 보수적인 대체에 대한 콜론과 반원형 대체에 대한 기간을 포함한다.많은 시퀀스 시각화 프로그램은 또한 색상을 사용하여 개별 시퀀스 요소의 특성에 대한 정보를 표시한다; DNA와 RNA 시퀀스에서 이것은 각 뉴클레오티드 고유의 색상을 할당하는 것과 같다.위의 이미지에 있는 것과 같은 단백질 정렬에서 색상은 종종 주어진 아미노산 대체물의 보존을 판단하는 데 도움이 되는 아미노산 특성을 나타내기 위해 사용된다.다중 시퀀스의 경우 각 열의 마지막 행은 정렬에 의해 결정되는 일치 시퀀스인 경우가 많다. 합의 시퀀스는 또한 각 뉴클레오티드 또는 아미노산 문자의 크기가 보존 정도에 해당하는 시퀀스 로고와 함께 그래픽 형식으로 표현되기도 한다.[5]

시퀀스 얼라인먼트는 다양한 텍스트 기반 파일 형식으로 저장할 수 있으며, 이 중 상당수는 원래 특정 얼라인먼트 프로그램 또는 구현과 함께 개발되었다.대부분의 웹 기반 도구는 FASTA 형식과 GenBank 형식과 같이 제한된 수의 입력 및 출력 형식을 허용하며 출력은 쉽게 편집할 수 없다.READSEQ 및 EMBOSS와 같이 그래픽 및/또는 명령줄 인터페이스를 제공하는 여러 변환 프로그램을 사용할[dead link] 수 있다.또한 바이오피톤, 바이오루비, 바이오펄 등 이러한 전환 기능을 제공하는 여러 프로그래밍 패키지도 있다.SAM/BAM 파일은 COG(Compact Idiosyncratic Gapped Alignment Report) 문자열 형식을 사용하여 일련의 이벤트(예: 일치/미스매치, 삽입, 삭제)를 인코딩하여 참조에 대한 시퀀스의 정렬을 나타낸다.[6]

시가 형식

참고자료 : GTCGTAGTA
읽기: CACGTAG -TA
시가: 2S5M2D2M, 여기서:
2S = 2 소프트 클리핑(일치되지 않거나 일치하는 시퀀스보다 긴 읽기)
5M = 5개의 일치 또는 불일치
2D = 삭제 2개
2M = 2개의 일치 또는 불일치

면죄부 정렬 프로그램의 원래 시가 형식은 M 문자와의 불일치 또는 일치를 구분하지 않았다.

SAMv1 규격 문서는 새로운 시가 코드를 정의한다.대부분의 경우 모호한 구형 'M' 문자보다는 일치나 불일치를 나타내는 데 '='와 'X' 문자를 사용하는 것이 바람직하다.

시가 코드 BAM 정수 설명 쿼리 사용 참조 사용
M 0 정렬 일치(시퀀스 일치 또는 불일치할 수 있음) 네 네
I 1 참조에 삽입 네 아니요.
D 2 참조에서 삭제 아니요. 네
N 3 참조에서 건너뛴 영역 아니요. 네
S 4 소프트 클리핑(SEQ에 있는 클리핑된 시퀀스) 네 아니요.
H 5 하드 클리핑(클립된 시퀀스는 SEQ에 존재하지 않음) 아니요. 아니요.
P 6 패딩(패딩된 참조에서 삭제) 아니요. 아니요.
= 7 시퀀스 매치 네 네
X 8 시퀀스 불일치 네 네
  • "쿼리 일치"와 "레퍼런스 일치"는 시가 연산이 각각 쿼리 순서와 기준 시퀀스를 따라 정렬을 유발하는지 여부를 나타낸다.
  • H는 첫 번째 및/또는 마지막 작업으로만 존재할 수 있다.
  • S는 그것들과 시가 스트링의 끝 사이에 H 연산만 있을 수 있다.
  • mRNA 대 유전체 정렬의 경우 N 연산은 인트론을 나타낸다.다른 유형의 선형에서는 N의 해석이 정의되지 않는다.
  • M/I/S/=/X 연산의 길이의 합은 SEQ의 길이와 같아야 한다.

글로벌 및 로컬 선형

모든 시퀀스의 모든 잔여물을 정렬하려고 시도하는 전역 정렬은 쿼리 세트의 시퀀스가 비슷하고 크기가 대략 같을 때 가장 유용하다.(이는 글로벌 얼라인먼트가 시작되거나 간격에서 끝날 수 없음을 의미하지 않는다.)일반적인 글로벌 정렬 기법은 니들맨-다이나믹 프로그래밍을 기반으로 한 툰슈 알고리즘.국소 정렬은 유사성 영역 또는 유사한 시퀀스 모티브를 더 큰 시퀀스 컨텍스트 내에 포함하는 것으로 의심되는 서로 다른 시퀀스에 더 유용하다.Smith-Waterman 알고리즘은 동일한 동적 프로그래밍 방식을 기반으로 하지만 어떤 장소에서 시작하거나 종료할 수 있는 추가 선택사항이 있는 일반적인 로컬 정렬 방법이다.[4]

세미 글로벌 또는 "글로컬"(글로벌-로컬의 줄임말) 방법으로 알려진 하이브리드 메서드는 두 시퀀스의 가능한 부분 정렬을 검색한다(즉, 한 가지 또는 두 가지 시작과 한 쪽 또는 양쪽 끝의 조합이 정렬된 것으로 명시됨).이것은 특히 한 시퀀스의 다운스트림 부분이 다른 시퀀스의 업스트림 부분과 중복될 때 유용할 수 있다.이 경우 전역 정렬이나 로컬 정렬이 완전히 적절하지 않다. 즉, 전역 정렬은 겹침 영역을 벗어나도록 정렬을 강제 시도하지만 로컬 정렬은 겹침 영역을 완전히 포함하지 않을 수 있다.[7]반지구적 정렬이 유용한 또 다른 경우는 한 염기서열(예: 유전자 염기서열)이 짧고 다른 염기서열(예: 염색체 염기서열)이 매우 긴 경우다.이 경우 짧은 시퀀스는 전체적으로(완전하게) 정렬되어야 하지만 긴 시퀀스에 대해서는 로컬(부분적) 정렬만 필요하다.

유전자 데이터의 빠른 확장은 현재의 DNA 시퀀스 정렬 알고리즘의 속도에 도전한다.DNA 변종 발견을 위한 효율적이고 정확한 방법에 대한 필수적인 요구는 실시간 병렬 처리를 위한 혁신적인 접근법을 요구한다.광학 컴퓨팅 접근방식은 현재 전기 구현에 대한 유망한 대안으로 제시되었지만, 그 적용 가능성은 여전히 시험해야 한다[1].

쌍방향 정렬

페어 와이즈 시퀀스 정렬 방법을 사용하여 두 쿼리 시퀀스의 가장 잘 어울리는 부분(로컬 또는 전역) 정렬을 찾는다.쌍방향 맞춤은 한 번에 두 시퀀스 사이에만 사용할 수 있지만 계산이 효율적이며, 극단적인 정밀도를 요구하지 않는 방법(예: 질의 유사성이 높은 시퀀스를 데이터베이스 검색)에 사용하는 경우가 많다.쌍으로 정렬하는 세 가지 주요 방법은 도트 매트릭스 방법, 동적 프로그래밍 및 워드 방법이지만 다중 시퀀스 정렬 기법도 쌍으로 정렬할 수 있다.[1]각 방법마다 각각의 장점과 단점이 있지만, 세 쌍의 방법 모두 낮은 정보 콘텐츠의 반복적인 시퀀스(특히 정렬할 두 시퀀스에서 반복 횟수가 다른 경우)에 어려움을 겪는다.

최대 유니크 매치

주어진 쌍방향 정렬의 효용성을 정량화하는 한 가지 방법은 '최대 고유 일치(MUM)' 또는 두 쿼리 시퀀스에서 발생하는 최장 연속성이다.더 긴 MUM 시퀀스는 일반적으로 더 밀접한 관련성을 반영한다.[8]계산 생물학에서 게놈의 다중 시퀀스 정렬에서.MUM과 기타 잠재적 앵커의 식별은 MUMMER와 같은 대형 정렬 시스템의 첫 번째 단계다.닻은 두 게놈 사이에 있는 영역으로, 두 게놈은 매우 유사하다.MOM이 무엇인지 이해하기 위해서 우리는 약자의 각 단어를 분해할 수 있다.일치는 정렬할 두 시퀀스에서 하위 문자열이 발생함을 의미한다.Unique는 하위 문자열이 각 시퀀스에서 한 번만 발생함을 의미한다.마지막으로, 최대값은 하위 문자열은 이전의 요구 사항을 모두 충족하는 또 다른 큰 문자열의 일부가 아니라고 명시한다.이것의 이면에 있는 아이디어는 각 게놈에서 정확히 일치하고 단 한 번만 발생하는 긴 시퀀스는 거의 확실히 전지구적 정렬의 일부분이라는 것이다.

더 정확히 말하자면:

"A와 B의 게놈 2개를 감안할 때, MUM(Maximal Unique Match) 하위 문자열은 특정 최소 길이 d(기본적으로 d= 20)보다 긴 A와 B의 공통 하위 문자열이다.

  • 최대치(즉, 불일치 없이 양쪽 끝에서 연장할 수 없음)이다.
  • 두 시퀀스에서 모두 고유함"[9]

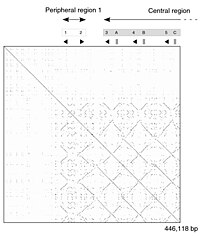
도트 매트릭스 방법

주요 기사:점 그림(생물정보학)
생쥐 변종 게놈의 일부에 대한 자가 비교.점도표는 DNA의 중복된 부분을 보여주는 선들의 조각들을 보여준다.
지역적 자기 유사성을 보여주는 휴먼진크 손가락 끝 설명 인자(GenBank ID NM_002383)의 DNA 점 그림.주 대각선은 시퀀스 자체와의 정렬을 나타내며, 주 대각선에서 벗어난 선은 시퀀스 내에서 유사하거나 반복적인 패턴을 나타낸다.이것은 전형적인 재발 음모의 예다.

개별 시퀀스 영역에 대한 정렬 패밀리를 암묵적으로 생성하는 도트 매트릭스 접근법은 대규모로 분석하는 데 시간이 걸리지만 질적이고 개념적으로 단순하다.노이즈가 없을 경우 도트 매트릭스 플롯에서 삽입, 삭제, 반복측정 또는 반전 반복측정 등의 특정 시퀀스 특징을 시각적으로 쉽게 식별할 수 있다.도트 매트릭스 그림을 구성하기 위해 2차원 행렬의 맨 위 행과 맨 왼쪽 열을 따라 두 시퀀스를 작성하고 적절한 열의 문자들이 일치하는 지점에 점을 배치한다. 이는 전형적인 반복 그림이다.일부 구현에서는 보수적인 대체물을 수용하기 위해 두 문자의 유사성 정도에 따라 점의 크기나 강도를 달리한다.매우 밀접하게 연관된 시퀀스의 점 그림은 행렬의 주 대각선을 따라 하나의 선으로 나타날 것이다.

정보 표시 기법으로서 도트 플롯의 문제는 다음과 같다: 노이즈, 명확성 결여, 비직관성, 일치 요약 통계 추출의 어려움 및 두 시퀀스의 일치 위치.또한 일치 데이터가 대각선에 걸쳐 본질적으로 중복되고 실제 플롯 영역의 대부분을 빈 공간이나 노이즈에 의해 차지하며 마지막으로 점-플롯은 두 개의 시퀀스로 제한되는 낭비되는 공간도 많다.이러한 제한사항은 Miropeats 선형 다이어그램에는 적용되지 않지만, 그들만의 특별한 결함이 있다.

점 그림은 또한 단일 시퀀스로 반복성을 평가하는 데 사용될 수 있다.시퀀스는 그 자체에 대해 플롯될 수 있으며, 유의미한 유사성을 공유하는 영역은 주 대각선을 벗어난 선으로 나타날 것이다.이 효과는 단백질이 여러 개의 유사한 구조 영역으로 구성되었을 때 발생할 수 있다.

동적 프로그래밍

동적 프로그래밍 기법은 Needleman-Wunsch 알고리즘을 통해 전역 정렬을, Smith-Waterman 알고리즘을 통해 로컬 정렬을 생성하기 위해 적용할 수 있다.일반적인 사용법에서 단백질 정렬은 대체 매트릭스를 사용하여 아미노산 일치 또는 불일치에 점수를 할당하고, 아미노산을 한 시퀀스로 다른 시퀀스의 간격과 일치시키는 갭 벌칙을 사용한다.DNA와 RNA 맞춤은 채점 매트릭스를 사용할 수 있지만, 실제로는 단순히 양성 일치 점수, 음성 불일치 점수, 음성 간격 벌점을 할당하는 경우가 많다.(표준 동적 프로그래밍에서 각 아미노산 위치의 점수는 이웃의 아이덴티티와 독립적이므로 베이스 쌓기 효과는 고려하지 않는다.그러나 알고리즘을 수정함으로써 그러한 영향을 설명할 수 있다.)표준 선형 격차 비용에 대한 공통적인 확장은 격차 개방과 격차 확장에 대해 서로 다른 두 가지 격차 벌칙을 사용하는 것이다.전형적으로 전자는 후자보다 훨씬 크다. 예를 들어 갭 개방의 경우 -10, 갭 확장의 경우 -2.따라서 정렬의 간격은 대개 줄어들고 잔여물과 간격은 함께 유지되기 때문에 일반적으로 생물학적 의미가 더 크다.고토 알고리즘은 3개의 매트릭스를 사용하여 아핀 갭 비용을 구현한다.

동적 프로그래밍은 뉴클레오티드(nucleotide)를 단백질 시퀀스에 정렬하는 데 유용할 수 있는데, 이 작업은 프레임 임시 변이(일반적으로 삽입 또는 삭제)를 고려할 필요성으로 인해 복잡하다.프레임서치 방법은 질의 핵산염 순서와 단백질 시퀀스 검색 세트 사이의 일련의 전역 또는 국소 쌍 정렬을 생성하거나, 그 반대의 경우도 마찬가지다.임의의 수의 뉴클레오티드에 의해 상쇄되는 프레임 편차를 평가하는 그것의 능력은 많은 수의 인델을 포함하는 시퀀스에 이 방법을 유용하게 만들며, 이것은 더 효율적인 휴리스틱 방법들과 일치시키기가 매우 어려울 수 있다.실제로 이 방법은 다량의 컴퓨팅 파워나 동적 프로그래밍에 특화된 아키텍처를 가진 시스템을 필요로 한다.블라스트와 EMBOSS 스위트는 변환된 선형을 만들기 위한 기본 도구를 제공한다(그러나 이러한 접근법 중 일부는 도구의 시퀀스 검색 기능의 부작용을 이용한다).보다 일반적인 방법은 GeneWise와 같은 오픈 소스 소프트웨어에서 이용할 수 있다.

동적 프로그래밍 방법은 특정 채점 기능이 주어지면 최적의 정렬을 찾을 수 있도록 보장되지만, 좋은 채점 함수를 식별하는 것은 이론적인 문제가 아니라 경험적인 문제인 경우가 많다.동적 프로그래밍은 세 개 이상의 시퀀스로 확장될 수 있지만, 많은 시퀀스 또는 매우 긴 시퀀스에서는 엄청나게 느리다.

워드 메서드

k-tuple method라고도 하는 워드 메소드는 최적의 정렬 솔루션을 찾을 수 있도록 보장되지 않지만 동적 프로그래밍보다 훨씬 효율적인 휴리스틱 방법이다.이러한 방법은 후보 시퀀스의 상당 부분이 본질적으로 쿼리 시퀀스와 유의한 일치점이 없을 것으로 이해되는 대규모 데이터베이스 검색에서 특히 유용하다.단어 방법은 데이터베이스 검색 도구인 FASTA와 블라스트 제품군에서 구현한 것으로 가장 잘 알려져 있다.[1]단어 방법은 쿼리 시퀀스에서 일련의 짧은 겹치지 않는 반복("words")을 식별하며, 이는 후보 데이터베이스 시퀀스와 일치한다.비교 중인 두 시퀀스에서 단어의 상대적 위치는 오프셋을 얻기 위해 감산된다. 이는 여러 개의 고유 단어가 동일한 오프셋을 생성하는 경우 정렬 영역을 나타낸다.이 영역이 감지되는 경우에만 이러한 방법은 보다 민감한 정렬 기준을 적용하므로, 눈에 띄는 유사성이 없는 시퀀스와의 불필요한 비교는 많이 제거된다.

FASTA 방법에서 사용자는 데이터베이스를 검색할 단어 길이로 사용할 값 k를 정의한다.이 방법은 속도가 느리지만 k의 낮은 값에서 더 민감하며, 매우 짧은 쿼리 시퀀스를 포함하는 검색에서도 선호된다.VOLAST 검색 방법군은 먼 관련 시퀀스 일치 검색과 같은 특정 유형의 쿼리에 최적화된 여러 알고리즘을 제공한다.블라스트는 많은 정확성을 희생하지 않고 FASTA에 대한 보다 빠른 대안을 제공하기 위해 개발되었다. FASTA와 같이, 블라스트는 길이 k의 단어 검색을 사용하지만, 가장 중요한 단어 일치만을 평가하지 않고, FASTA와 같은 모든 단어 일치만을 평가한다.대부분의 VLAST 구현은 쿼리 및 데이터베이스 유형에 최적화된 고정된 기본 단어 길이를 사용하며, 반복적이거나 매우 짧은 쿼리 시퀀스로 검색할 때와 같은 특수한 상황에서만 변경된다.구현은 EMBL FASTA, NCBI BRAAST와 같은 다수의 웹 포털을 통해 확인할 수 있다.

다중 시퀀스 정렬

주요 기사:다중 시퀀스 정렬
잔류물 보존(상단) 및 잔류물 특성(하단)으로 색칠된 27개 조류 인플루엔자 헤마글루틴 단백질 시퀀스 정렬

다중 시퀀스 정렬은 한 번에 세 개 이상의 시퀀스를 통합하기 위한 쌍방향 정렬의 확장이다.다중 정렬 방법은 주어진 쿼리 세트의 모든 시퀀스를 정렬하려고 시도한다.다중 선형은 진화적으로 관련이 있다고 가정된 시퀀스 그룹 전체에 걸쳐 보존된 시퀀스 영역을 식별하는 데 종종 사용된다.이러한 보존된 시퀀스 모티브는 효소의 촉매 활성 부위를 찾기 위해 구조 및 기계론적 정보와 함께 사용할 수 있다.선형은 또한 계통생식을 형성함으로써 진화적 관계를 확립하는 데 도움을 주기 위해 사용된다.다중 시퀀스 정렬은 계산적으로 생성하기 어렵고 문제의 대부분의 공식은 NP-완전한 조합 최적화 문제를 야기한다.[10][11]그럼에도 불구하고 생물정보학에서 이러한 정렬의 효용성은 세 개 이상의 시퀀스를 정렬하는 데 적합한 다양한 방법을 개발하게 했다.

동적 프로그래밍

동적 프로그래밍의 기법은 이론적으로 많은 수의 시퀀스에 적용할 수 있지만, 시간과 메모리 모두에서 계산적으로 비용이 많이 들기 때문에 가장 기본적인 형태에서 서너 개 이상의 시퀀스에 거의 사용되지 않는다.이 방법은 두 개의 시퀀스에서 형성된 시퀀스 매트릭스와 n차원 등가물을 구성할 것을 요구한다. 여기서 n은 쿼리의 시퀀스 수입니다.표준 동적 프로그래밍은 먼저 모든 질의 시퀀스 쌍에 사용되며, 그 다음 중간 위치에서 가능한 일치 또는 간격을 고려하여 "정렬 공간"을 채워서, 결국 각 2 시퀀스 정렬 사이에 기본적으로 정렬을 구성한다.이 기술은 계산적으로 비용이 많이 들지만, 몇 개의 시퀀스만 정확하게 정렬하면 되는 경우에 글로벌 최적 솔루션의 보장이 유용하다.「쌍의 합계」 목표함수에 의존하는 동적 프로그래밍의 연산 요구를 줄이는 한 가지 방법이 MSA 소프트웨어 패키지에 구현되었다.[12]

프로그레시브 방식

진행형, 계층형 또는 트리 방식은 먼저 가장 유사한 시퀀스를 정렬하고 전체 쿼리 세트가 솔루션에 통합될 때까지 연속적으로 관련성이 낮은 시퀀스 또는 그룹을 정렬에 추가함으로써 다중 시퀀스 정렬을 생성한다.시퀀스 관련성을 설명하는 초기 트리는 FASTA와 유사한 경험적 페어 와이즈 정렬 방법을 포함할 수 있는 페어 와이즈 비교를 기반으로 한다.점진적 정렬 결과는 "가장 관련성이 높은" 시퀀스의 선택에 따라 달라지므로 초기 쌍방향 정렬의 부정확성에 민감할 수 있다.대부분의 점진적인 다중 시퀀스 정렬 방법은 연관성에 따라 쿼리 세트의 시퀀스에 가중치를 추가하므로 초기 시퀀스를 제대로 선택할 가능성이 낮아져 정렬 정확도가 향상된다.

Clustal Progression 구현의[13][14][15] 많은 변화는 다중 시퀀스 정렬, 계통발생 트리 구축 및 단백질 구조 예측을 위한 입력으로 사용된다.더 느리지만 더 정확한 진행 방법의 변형을 T-Coffee라고 한다.[16]

반복적 방법

반복적 방법은 초기 쌍방향 맞춤의 정확성에 대한 의존도가 높은 것을 개선하려고 시도하는데, 이는 점진적 방법의 약점이다.반복 방법은 초기 전역 정렬을 할당하고 시퀀스 하위 집합을 다시 정렬하여 선택된 정렬 점수 계산 방법에 따라 객관적 기능을 최적화한다.그런 다음 재조정된 하위 집합은 다음 반복의 다중 시퀀스 정렬을 생성하기 위해 자체 정렬된다.시퀀스 부분군 선택 방법 및 객관적 기능을 다양하게 검토한다.[17]

모티브 찾기

프로파일 분석이라고도 하는 모티프 소견은 쿼리 세트의 시퀀스 간에 보존된 짧은 시퀀스 모티브를 정렬하는 글로벌 다중 시퀀스 정렬을 구성한다.이는 일반적으로 먼저 일반적인 전역 다중 시퀀스 정렬을 구성하여 수행되며, 그 후에 보존도가 높은 영역이 분리되어 일련의 프로파일 매트릭스를 구성하는데 사용된다.보존된 각 영역에 대한 프로파일 매트릭스는 채점 매트릭스처럼 배열되지만 각 위치에서 아미노산 또는 뉴클레오티드의 빈도수는 보다 일반적인 경험적 분포가 아닌 보존된 영역의 문자 분포에서 도출된다.그런 다음 프로파일 행렬을 사용하여 다른 시퀀스에서 특성화하는 모티브의 발생 여부를 검색한다.원본 데이터 세트에 적은 수의 시퀀스 또는 관련성이 높은 시퀀스만 포함된 경우, 유사 마운트를 추가하여 모티브에 표시된 문자 분포를 정규화한다.

컴퓨터 과학에서 영감을 받은 기술

다중 시퀀스 정렬을 모델링하는 프로파일 HMM

컴퓨터 공학에서 일반적으로 사용되는 다양한 일반 최적화 알고리즘이 다중 시퀀스 정렬 문제에도 적용되었다.Hidden Markov 모델은 주어진 질의 집합에 대해 가능한 다중 시퀀스 정렬의 패밀리에 대한 확률 점수를 생성하는 데 사용되어 왔다. 초기 HMH 기반 방법에서 성능 저하 없음에도 불구하고, 이후 애플리케이션은 소음에 덜 취약하기 때문에 원격과 관련된 시퀀스를 검출하는 데 특히 효과적이라는 것을 발견했다.e 보수적 또는 반원적 대체에 의해 생성된다.[18]유전자 알고리즘과 시뮬레이션된 어닐링은 또한 점수 합계법과 같은 채점 함수에 의해 판단되는 다중 시퀀스 정렬 점수를 최적화하는 데 사용되어 왔다.보다 완전한 세부사항과 소프트웨어 패키지는 본문 다중 시퀀스 정렬에서 확인할 수 있다.

버로우스-휠러 변환은 Bowtie, BWA와 같은 인기 있는 도구에서 빠른 단축 읽기 정렬에 성공적으로 적용되었다.FM-색인을 참조하십시오.

구조 정렬

주요 기사:구조 정렬

대개 단백질과 때로는 RNA 염기서열로 한정되는 구조 정렬은 단백질이나 RNA 분자의 2차 및 3차 구조에 대한 정보를 사용하여 염기서열 정렬을 돕는다.이러한 방법은 둘 이상의 시퀀스에 사용할 수 있으며 일반적으로 로컬 정렬을 생성할 수 있지만, 구조 정보의 가용성에 따라 달라지기 때문에 (대개 X선 결정학 또는 NMR 분광학을 통해) 해당 구조가 알려진 시퀀스에만 사용할 수 있다.단백질과 RNA 구조는 모두 시퀀스보다 진화적으로 보존되어 있기 때문에,[19] 구조 정렬은 매우 멀리 떨어져 있고 시퀀스 비교가 그들의 유사성을 신뢰성 있게 감지할 수 없을 정도로 광범위하게 갈라진 시퀀스 사이의 신뢰성이 더 높을 수 있다.

구조 정렬은 순서 정보에 전적으로 의존하지 않고 구조적으로 유사한 단백질 시퀀스 영역을 명시적으로 정렬하기 때문에 호몰로지 기반 단백질 구조 예측을[20] 위한 정렬을 평가할 때 "금색 표준"으로 사용된다.그러나 구조물을 알 수 없는, 적어도 쿼리 집합에서 하나 이상의 시퀀스가 모델링할 대상이기 때문에 구조 예측에 명확한 구조 선형을 사용할 수 없다.대상과 템플릿 시퀀스 사이의 구조 정렬을 고려할 때 대상 단백질 시퀀스의 고도로 정확한 모델을 생성할 수 있다는 것이 입증되었다. 동종학 기반 구조 예측의 주요 걸림돌은 시퀀스 정보만 주어진 구조적으로 정확한 정렬의 생산이다.[20]

달리

DALI 방법 또는 거리 행렬 정렬은 질의 시퀀스에서 연속적인 육각화 사이의 접촉 유사성 패턴을 기반으로 구조 정렬을 구성하는 단편 기반 방법이다.[21]그것은 쌍방향 또는 다중 선형을 생성할 수 있고 PDB(단백질 데이터 뱅크)에서 질의 시퀀스의 구조적 인접성을 식별할 수 있다.FSSP 구조 정렬 데이터베이스(단백질의 구조-구조 정렬에 기초한 폴드 분류, 또는 구조적으로 유사한 단백질의 가족) 구축에 이용되어 왔다.DALI 웹서버는 DALI에서 접속할 수 있으며 금감원은 Dali Database에 위치한다.

SSAP

SSAP(Sequential Structure Alignment Program)는 구조물 공간에서 원자 대 원자 벡터를 비교점으로 사용하는 동적 프로그래밍 기반의 구조 정렬 방식이다.쌍방향 맞춤뿐만 아니라 복수의 선형을 포함하도록 원래 설명 이후 확장되었으며,[22] 단백질 접힘의 CAT(Class, Architecture, Topology, Homology) 계층적 데이터베이스 분류 구축에 사용되었다.[23]CAT 데이터베이스는 CAT 단백질 구조 분류에서 액세스할 수 있다.

결합연장

구조 정렬의 결합 연장법은 국부 기하학을 이용하여 분석 중인 두 단백질의 짧은 파편을 정렬시킨 다음 이 파편을 더 큰 정렬로 조립함으로써 쌍방향 구조 정렬을 생성한다.[24]강체-근위 평균 제곱 거리, 잔류 거리, 국소 이차 구조 등의 조치와 잔류 인접 소수성 등의 주변 환경적 특징에 기초하여 " 정렬된 조각 쌍"이라 불리는 국소 정렬을 생성하여 사전 내에 가능한 모든 구조 정렬을 나타내는 유사 행렬을 구축한다.정의된 컷오프 기준한 단백질 구조 상태에서 다른 단백질 구조 상태까지의 경로는 한 번에 한 조각씩 성장하는 정렬을 확장함으로써 행렬을 통해 추적된다.최적 그러한 경로는 결합-확장 정렬을 정의한다.이 방법을 구현하고 단백질 데이터 뱅크에서 구조물의 쌍방향 정렬 데이터베이스를 제공하는 웹 기반 서버는 결합 연장 웹사이트에 위치한다.

계통학적 분석

주요 기사:컴퓨터 계통 유전학

염기생성학 및 염기서열 정렬은 염기서열 관련성 평가의 공통 필요성 때문에 밀접하게 연관되어 있는 분야다.[25]계통유전학 분야는 계통유전종의 유전체에서 대표되는 동질유전자의 진화적 관계를 분류하는 데 사용되는 계통유전수의 구성과 해석에 있어서 시퀀스 얼라인먼트를 광범위하게 이용한다.질의 집합에서 시퀀스가 다른 정도는 질적으로 시퀀스의 서로 진화적 거리와 관련이 있다.대략적으로 높은 순서의 정체성은 문제의 순서가 비교적 젊은 가장 최근의 공통 조상을 가지고 있음을 시사하는 반면, 낮은 정체성은 그 차이가 더 고대의 것임을 암시한다.이 근사치는 두 유전자가 처음 분리한 이후 경과된 시간(즉, 병합 시간)을 추론하는 데 대략적으로 일정한 진화 변화율을 사용할 수 있다는 "분자 시계" 가설을 반영하여, 돌연변이와 선택 효과가 시퀀스 선에 걸쳐 일정하다고 가정한다.따라서 DNA 수리 비율이나 특정 지역의 기능적 보존에 있어 유기체나 종 사이의 가능한 차이는 순차적으로 설명하지 않는다.(뉴클레오티드 시퀀스의 경우, 가장 기본적인 형태의 분자시계 가설은 또한 주어진 코돈의 의미를 바꾸지 않는 무성 돌연변이와 다른 아미노산이 단백질에 통합되는 결과를 초래하는 다른 돌연변이의 허용률의 차이를 할인한다.)보다 통계적으로 정확한 방법을 사용하면 계통생성 나무의 각 가지에 있는 진화율이 변화할 수 있으며, 따라서 유전자의 합체 시간에 대한 더 나은 추정치를 산출할 수 있다.

점진적인 다중 정렬 기법은 관련성 순서로 증가하는 정렬에 시퀀스를 통합하기 때문에 필요에 따라 계통 생성 트리를 생성한다.다중 시퀀스 정렬과 계통 발생 트리를 조립하는 다른 기법에서는 먼저 트리를 점수화하고 정렬하고 가장 높은 점수 트리에서 다중 시퀀스 정렬을 계산한다.흔히 사용되는 계통생성 트리구축 방법은 최적의 다중 시퀀스 정렬 선택 문제처럼 최적의 트리를 선택하는 문제가 NP-hard이기 때문에 주로 휴리스틱하다.[26]

유의성 평가

시퀀스 정렬은 생물정보학에서 시퀀스 유사성을 식별하고 계통생성 나무를 생성하며 단백질 구조의 동질학 모델을 개발하는 데 유용하다.그러나 시퀀스 정렬의 생물학적 관련성이 항상 명확한 것은 아니다.맞춤은 흔히 공통의 조상으로부터 내려온 염기서열들 사이의 진화적 변화 정도를 반영하는 것으로 가정되지만, 융합적 진화가 발생하여 진화론적으로 무관하지만 유사한 기능을 수행하고 유사한 구조를 가진 단백질들 사이에 명백한 유사성을 만들어낼 수 있다는 것은 공식적으로 가능하다.

블라스트와 같은 데이터베이스 검색에서 통계적 방법은 검색되는 데이터베이스의 크기와 구성을 고려할 때 우연히 발생하는 시퀀스 또는 시퀀스 영역 간의 특정 정렬 가능성을 결정할 수 있다.이러한 값은 검색 공간에 따라 크게 달라질 수 있다.특히 데이터베이스가 질의 순서와 동일한 유기체의 시퀀스로만 구성된 경우 우연한 기회에 의해 주어진 정렬을 찾을 가능성이 높아진다.데이터베이스나 쿼리의 반복 시퀀스는 또한 검색 결과와 통계적 유의성의 평가를 모두 왜곡시킬 수 있다; 블라스트는 통계적 인공물인 명백한 타격을 피하기 위해 쿼리의 반복 시퀀스를 자동으로 필터링한다.

절단된 시퀀스 선형에 대한 통계적 유의성 추정 방법은 문헌에 수록되어 있다.[25][27][28][29][30][31][32][33]

신뢰도 평가

통계적 유의성은 주어진 품질의 정렬이 우연히 발생할 수 있는 확률을 나타내지만, 주어진 정렬이 동일한 시퀀스의 대체 정렬에 얼마나 우월한지는 나타내지 않는다.정렬 신뢰도 측정은 주어진 시퀀스 쌍에 대한 최선의 점수 맞춤이 실질적으로 유사한 정도를 나타낸다.절단된 시퀀스 선형에 대한 정렬 신뢰도 추정 방법은 문헌에 수록되어 있다.[34]

채점 기능

알려진 시퀀스에 대한 생물학적 또는 통계적 관찰을 반영하는 채점 함수의 선택은 좋은 선형을 생성하는 데 중요하다.단백질 시퀀스는 주어진 문자 대 문자 대체의 확률을 반영하는 대체 행렬을 사용하여 정렬되는 경우가 많다.PAM 매트릭스(Point Accepted Mutiation Matrix, 원래 마가렛 데이호프가 정의하고 때로는 "데이호프 매트릭스"라고 지칭)라고 하는 일련의 매트릭스는 특정 아미노산 돌연변이의 비율과 확률에 관한 진화적 근사치를 명시적으로 암호화한다.BLOSUM(Blocks Substitution Matrix)으로 알려진 또 다른 일반적인 점수 매트릭스 시리즈는 경험적으로 도출된 대체 확률을 암호화한다.두 유형의 행렬의 변형은 차이 수준의 차이를 가진 시퀀스를 감지하기 위해 사용되므로, VOLAS 또는 FASTA 사용자는 더 밀접하게 관련된 일치 항목으로 검색을 제한하거나 더 다양한 시퀀스를 탐지하도록 확장할 수 있다.갭 벌칙은 뉴클레오티드와 단백질 시퀀스 모두에서 진화 모델, 삽입 또는 삭제 돌연변이의 도입에 대해 설명하며, 따라서 벌칙 값은 그러한 돌연변이의 예상 속도에 비례해야 한다.따라서 생산된 정렬의 품질은 채점 기능의 품질에 따라 달라진다.

매트릭스 및/또는 갭 페널티 값을 점수 매트릭스 및/또는 갭 페널티 값을 서로 다르게 선택하여 동일한 정렬을 여러 번 시도하고 결과를 비교하는 것은 매우 유용하고 유익할 수 있다.솔루션이 취약하거나 고유하지 않은 영역은 선형 매개변수의 변동에 강한 선형 영역을 관찰하여 식별할 수 있다.

기타 생물학적 용도

표현된 시퀀스 태그와 전체 길이 mRNA와 같은 시퀀스 RNA는 시퀀스화된 게놈에 맞춰 유전자가 있는 곳을 찾아내고 대체 스플라이싱과[35] RNA 편집에 대한 정보를 얻을 수 있다.[36]시퀀스 정렬은 게놈 어셈블리의 일부로서, 콘티그(서열의 긴 연장)가 형성될 수 있도록 시퀀스가 중첩을 찾기 위해 정렬된다.[37]또 다른 용도는 SNP 분석으로, 모집단에서 종종 다른 단일 기저귀를 찾기 위해 서로 다른 개인의 시퀀스가 정렬된다.[38]

비생물학적 용도

생물학적 시퀀스 정렬에 사용되는 방법은 다른 분야, 특히 자연 언어 처리 및 사회과학 분야에서도 응용 분야를 발견했는데, 여기서 Needleman-Wunsch 알고리즘은 보통 Optimal matching이라고 한다.[39]자연어 생성 알고리즘에서 단어가 선택될 요소 집합을 생성하는 기법은 생물정보학으로부터 다중 시퀀스 정렬 기법을 차용해 컴퓨터 생성 수학적 증명들의 언어적 버전을 만들어냈다.[40]역사적·비교적 언어학 분야에서는 언어학자들이 전통적으로 언어를 재구성하는 비교 방법을 부분적으로 자동화하기 위해 시퀀스 정렬이 사용되어 왔다.[41]비즈니스·마케팅 연구에서도 시간 경과에 따른 일련의 구매를 분석하는 데 복수의 시퀀스 정렬 기법을 적용했다.[42]

소프트웨어

주요 기사:시퀀스 정렬 소프트웨어

시퀀스 정렬 소프트웨어에는 알고리즘과 정렬 유형별로 분류된 사용 가능한 소프트웨어의 보다 완전한 목록이 제공되지만, 일반적인 시퀀스 정렬 작업에 사용되는 공통 소프트웨어 도구는 정렬을 위한 ClustalW2와[43] T-coffee[44], 데이터베이스 검색을 위한 VLAST[45] 및 FASTA3x[46] 등이 있다.DESTAR Lasergene, Genious, Pattern 등의 상용 도구헌터도 이용할 수 있다.시퀀스 정렬 수행으로 주석을 달은 공구는 바이오에 나열되어 있다.도구 레지스트리

정렬 알고리즘과 소프트웨어는 BALIBASE라고 알려진 표준화된 기준 다중 시퀀스 정렬 세트를 사용하여 서로 직접 비교할 수 있다.[47]데이터 세트는 순서에 기반한 방법을 비교하는 표준으로 간주될 수 있는 구조 정렬로 구성된다.자주 발생하는 정렬 문제에 대한 많은 공통 정렬 방법의 상대적 성능은 표로 작성되었으며, BALIBASE에서 온라인으로 게시된 결과를 선별하였다.[48][49]BALIB의 포괄적인 목록많은 (현재 12개) 서로 다른 정렬 도구에 대한 ASE 점수는 단백질 워크벤치 STRACE 내에서 계산할 수 있다.[50]

참고 항목

참조

  1. ^ a b c Mount DM. (2004). Bioinformatics: Sequence and Genome Analysis (2nd ed.). Cold Spring Harbor Laboratory Press: Cold Spring Harbor, NY. ISBN 978-0-87969-608-5.
  2. ^ "Clustal FAQ #Symbols". Clustal. Archived from the original on 24 October 2016. Retrieved 8 December 2014.
  3. ^ Ng PC; Henikoff S (May 2001). "Predicting deleterious amino acid substitutions". Genome Res. 11 (5): 863–74. doi:10.1101/gr.176601. PMC 311071. PMID 11337480.
  4. ^ a b Polyanovsky, V. O.; Roytberg, M. A.; Tumanyan, V. G. (2011). "Comparative analysis of the quality of a global algorithm and a local algorithm for alignment of two sequences". Algorithms for Molecular Biology. 6 (1): 25. doi:10.1186/1748-7188-6-25. PMC 3223492. PMID 22032267. S2CID 2658261.
  5. ^ Schneider TD; Stephens RM (1990). "Sequence logos: a new way to display consensus sequences". Nucleic Acids Res. 18 (20): 6097–6100. doi:10.1093/nar/18.20.6097. PMC 332411. PMID 2172928.
  6. ^ "Sequence Alignment/Map Format Specification" (PDF).
  7. ^ Brudno M; Malde S; Poliakov A; Do CB; Couronne O; Dubchak I; Batzoglou S (2003). "Glocal alignment: finding rearrangements during alignment". Bioinformatics. 19. Suppl 1 (90001): i54–62. doi:10.1093/bioinformatics/btg1005. PMID 12855437.
  8. ^ Delcher, A. L.; Kasif, S.; Fleishmann, R.D.; Peterson, J.; White, O.; Salzberg, S.L. (1999). "Alignment of whole genomes". Nucleic Acids Research. 27 (11): 2369–2376. doi:10.1093/nar/30.11.2478. PMC 148804. PMID 10325427.
  9. ^ Wing-Kin, Sung (2010). Algorithms in Bioinformatics: A Practical Introduction (First ed.). Boca Raton: Chapman & Hall/CRC Press. ISBN 978-1420070330.
  10. ^ Wang L; Jiang T. (1994). "On the complexity of multiple sequence alignment". J Comput Biol. 1 (4): 337–48. CiteSeerX 10.1.1.408.894. doi:10.1089/cmb.1994.1.337. PMID 8790475.
  11. ^ Elias, Isaac (2006). "Settling the intractability of multiple alignment". J Comput Biol. 13 (7): 1323–1339. CiteSeerX 10.1.1.6.256. doi:10.1089/cmb.2006.13.1323. PMID 17037961.
  12. ^ Lipman DJ; Altschul SF; Kececioglu JD (1989). "A tool for multiple sequence alignment". Proc Natl Acad Sci USA. 86 (12): 4412–5. Bibcode:1989PNAS...86.4412L. doi:10.1073/pnas.86.12.4412. PMC 287279. PMID 2734293.
  13. ^ Higgins DG, Sharp PM (1988). "CLUSTAL: a package for performing multiple sequence alignment on a microcomputer". Gene. 73 (1): 237–44. doi:10.1016/0378-1119(88)90330-7. PMID 3243435.
  14. ^ Thompson JD; Higgins DG; Gibson TJ. (1994). "CLUSTAL W: improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice". Nucleic Acids Res. 22 (22): 4673–80. doi:10.1093/nar/22.22.4673. PMC 308517. PMID 7984417.
  15. ^ Chenna R; Sugawara H; Koike T; Lopez R; Gibson TJ; Higgins DG; Thompson JD. (2003). "Multiple sequence alignment with the Clustal series of programs". Nucleic Acids Res. 31 (13): 3497–500. doi:10.1093/nar/gkg500. PMC 168907. PMID 12824352.
  16. ^ Notredame C; Higgins DG; Heringa J. (2000). "T-Coffee: A novel method for fast and accurate multiple sequence alignment". J Mol Biol. 302 (1): 205–17. doi:10.1006/jmbi.2000.4042. PMID 10964570. S2CID 10189971.
  17. ^ Hirosawa M; Totoki Y; Hoshida M; Ishikawa M. (1995). "Comprehensive study on iterative algorithms of multiple sequence alignment". Comput Appl Biosci. 11 (1): 13–8. doi:10.1093/bioinformatics/11.1.13. PMID 7796270.
  18. ^ Karplus K; Barrett C; Hughey R. (1998). "Hidden Markov models for detecting remote protein homologies". Bioinformatics. 14 (10): 846–856. doi:10.1093/bioinformatics/14.10.846. PMID 9927713.
  19. ^ Chothia C; Lesk AM. (April 1986). "The relation between the divergence of sequence and structure in proteins". EMBO J. 5 (4): 823–6. doi:10.1002/j.1460-2075.1986.tb04288.x. PMC 1166865. PMID 3709526.
  20. ^ a b Zhang Y; Skolnick J. (2005). "The protein structure prediction problem could be solved using the current PDB library". Proc Natl Acad Sci USA. 102 (4): 1029–34. Bibcode:2005PNAS..102.1029Z. doi:10.1073/pnas.0407152101. PMC 545829. PMID 15653774.
  21. ^ Holm L; Sander C (1996). "Mapping the protein universe". Science. 273 (5275): 595–603. Bibcode:1996Sci...273..595H. doi:10.1126/science.273.5275.595. PMID 8662544. S2CID 7509134.
  22. ^ Taylor WR; Flores TP; Orengo CA. (1994). "Multiple protein structure alignment". Protein Sci. 3 (10): 1858–70. doi:10.1002/pro.5560031025. PMC 2142613. PMID 7849601.
  23. ^ Orengo CA; Michie AD; Jones S; Jones DT; Swindells MB; Thornton JM (1997). "CATH--a hierarchic classification of protein domain structures". Structure. 5 (8): 1093–108. doi:10.1016/S0969-2126(97)00260-8. PMID 9309224.
  24. ^ Shindyalov IN; Bourne PE. (1998). "Protein structure alignment by incremental combinatorial extension (CE) of the optimal path". Protein Eng. 11 (9): 739–47. doi:10.1093/protein/11.9.739. PMID 9796821.
  25. ^ a b Ortet P; Bastien O (2010). "Where Does the Alignment Score Distribution Shape Come from?". Evolutionary Bioinformatics. 6: 159–187. doi:10.4137/EBO.S5875. PMC 3023300. PMID 21258650.
  26. ^ Felsenstein J. (2004). Inferring Phylogenies. Sinauer Associates: Sunderland, MA. ISBN 978-0-87893-177-4.
  27. ^ Altschul SF; Gish W (1996). Local Alignment Statistics. Meth.Enz. Methods in Enzymology. Vol. 266. pp. 460–480. doi:10.1016/S0076-6879(96)66029-7. ISBN 9780121821678. PMID 8743700.
  28. ^ Hartmann AK (2002). "Sampling rare events: statistics of local sequence alignments". Phys. Rev. E. 65 (5): 056102. arXiv:cond-mat/0108201. Bibcode:2002PhRvE..65e6102H. doi:10.1103/PhysRevE.65.056102. PMID 12059642. S2CID 193085.
  29. ^ Newberg LA (2008). "Significance of gapped sequence alignments". J Comput Biol. 15 (9): 1187–1194. doi:10.1089/cmb.2008.0125. PMC 2737730. PMID 18973434.
  30. ^ Eddy SR; Rost, Burkhard (2008). Rost, Burkhard (ed.). "A probabilistic model of local sequence alignment that simplifies statistical significance estimation". PLOS Comput Biol. 4 (5): e1000069. Bibcode:2008PLSCB...4E0069E. doi:10.1371/journal.pcbi.1000069. PMC 2396288. PMID 18516236. S2CID 15640896.
  31. ^ Bastien O; Aude JC; Roy S; Marechal E (2004). "Fundamentals of massive automatic pairwise alignments of protein sequences: theoretical significance of Z-value statistics". Bioinformatics. 20 (4): 534–537. doi:10.1093/bioinformatics/btg440. PMID 14990449.
  32. ^ Agrawal A; Huang X (2011). "Pairwise Statistical Significance of Local Sequence Alignment Using Sequence-Specific and Position-Specific Substitution Matrices". IEEE/ACM Transactions on Computational Biology and Bioinformatics. 8 (1): 194–205. doi:10.1109/TCBB.2009.69. PMID 21071807. S2CID 6559731.
  33. ^ Agrawal A; Brendel VP; Huang X (2008). "Pairwise statistical significance and empirical determination of effective gap opening penalties for protein local sequence alignment". International Journal of Computational Biology and Drug Design. 1 (4): 347–367. doi:10.1504/IJCBDD.2008.022207. PMID 20063463. Archived from the original on 28 January 2013.
  34. ^ Newberg LA; Lawrence CE (2009). "Exact Calculation of Distributions on Integers, with Application to Sequence Alignment". J Comput Biol. 16 (1): 1–18. doi:10.1089/cmb.2008.0137. PMC 2858568. PMID 19119992.
  35. ^ Kim N; Lee C (2008). Bioinformatics detection of alternative splicing. Methods in Molecular Biology. Vol. 452. pp. 179–97. doi:10.1007/978-1-60327-159-2_9. ISBN 978-1-58829-707-5. PMID 18566765.
  36. ^ Li JB, Levanon EY, Yoon JK, et al. (May 2009). "Genome-wide identification of human RNA editing sites by parallel DNA capturing and sequencing". Science. 324 (5931): 1210–3. Bibcode:2009Sci...324.1210L. doi:10.1126/science.1170995. PMID 19478186. S2CID 31148824.
  37. ^ Blazewicz J, Bryja M, Figlerowicz M, et al. (June 2009). "Whole genome assembly from 454 sequencing output via modified DNA graph concept". Comput Biol Chem. 33 (3): 224–30. doi:10.1016/j.compbiolchem.2009.04.005. PMID 19477687.
  38. ^ Duran C; Appleby N; Vardy M; Imelfort M; Edwards D; Batley J (May 2009). "Single nucleotide polymorphism discovery in barley using autoSNPdb". Plant Biotechnol. J. 7 (4): 326–33. doi:10.1111/j.1467-7652.2009.00407.x. PMID 19386041.
  39. ^ Abbott A.; Tsay A. (2000). "Sequence Analysis and Optimal Matching Methods in Sociology, Review and Prospect". Sociological Methods and Research. 29 (1): 3–33. doi:10.1177/0049124100029001001. S2CID 121097811.
  40. ^ Barzilay R; Lee L. (2002). "Bootstrapping Lexical Choice via Multiple-Sequence Alignment" (PDF). Proceedings of the Conference on Empirical Methods in Natural Language Processing (EMNLP). 10: 164–171. arXiv:cs/0205065. Bibcode:2002cs........5065B. doi:10.3115/1118693.1118715. S2CID 7521453.
  41. ^ Kondrak, Grzegorz (2002). "Algorithms for Language Reconstruction" (PDF). University of Toronto, Ontario. Archived from the original (PDF) on 17 December 2008. Retrieved 21 January 2007. {{cite journal}}:Cite 저널은 필요로 한다. journal=(도움말)
  42. ^ Prinzie A.; D. Van den Poel (2006). "Incorporating sequential information into traditional classification models by using an element/position-sensitive SAM". Decision Support Systems. 42 (2): 508–526. doi:10.1016/j.dss.2005.02.004. See also Prinzie and Van den Poel's paper Prinzie, A; Vandenpoel, D (2007). "Predicting home-appliance acquisition sequences: Markov/Markov for Discrimination and survival analysis for modeling sequential information in NPTB models". Decision Support Systems. 44 (1): 28–45. doi:10.1016/j.dss.2007.02.008.
  43. ^ EMBL-EBI. "ClustalW2 < Multiple Sequence Alignment < EMBL-EBI". www.EBI.ac.uk. Retrieved 12 June 2017.
  44. ^ 티커피
  45. ^ "BLAST: Basic Local Alignment Search Tool". blast.ncbi.nlm.NIH.gov. Retrieved 12 June 2017.
  46. ^ "UVA FASTA Server". fasta.bioch.Virginia.edu. Retrieved 12 June 2017.
  47. ^ Thompson JD; Plewniak F; Poch O (1999). "BAliBASE: a benchmark alignment database for the evaluation of multiple alignment programs". Bioinformatics. 15 (1): 87–8. doi:10.1093/bioinformatics/15.1.87. PMID 10068696.
  48. ^ 밸리베이스
  49. ^ Thompson JD; Plewniak F; Poch O. (1999). "A comprehensive comparison of multiple sequence alignment programs". Nucleic Acids Res. 27 (13): 2682–90. doi:10.1093/nar/27.13.2682. PMC 148477. PMID 10373585.
  50. ^ "Multiple sequence alignment: Strap". 3d-alignment.eu. Retrieved 12 June 2017.

외부 링크

이 기사 듣기(39분)
Spoken Wikipedia icon
이 오디오 파일은 2012년 6월 5일(2012-06-05) 날짜의 본 기사의 개정으로 생성되었으며, 이후 편집된 내용을 반영하지 않는다.
(오디오 도움말 · 더 많은 구어 기사)