스미스-워터맨 알고리즘

클래스	시퀀스 정렬
최악의 경우 공연
최악의 경우 공간 복잡성

단계를 점진적으로 보여주는 애니메이션 예. 자세한 단계는 여기를 참조하십시오.

Smith-Waterman 알고리즘은 두 개의 핵산 염기서열 또는 단백질 염기서열 사이의 유사한 영역을 결정하기 위해 로컬 염기서열 정렬을 수행한다. 전체 시퀀스를 보는 대신 스미스-워터맨 알고리즘은 가능한 모든 길이의 세그먼트를 비교하고 유사성 측정을 최적화한다.

이 알고리즘은 템플 F에 의해 처음 제안되었다. 스미스와 마이클 S. 1981년 워터맨.^[1] 니들맨처럼-Wunsch 알고리즘은 변형된 것으로서, Smith-Waterman은 동적 프로그래밍 알고리즘이다. 이와 같이 사용 중인 채점 시스템(대체 매트릭스 및 갭 점수 매트릭스 포함)과 관련하여 최적의 로컬 정렬을 찾을 수 있는 것이 보장되는 바람직한 특성을 가지고 있다. 니들맨의 주요 차이점-Wunsch 알고리즘은 음의 채점 매트릭스 셀이 0으로 설정되며, 이는 (양수 채점) 로컬 정렬을 시각적으로 렌더링한다. 트레이스백 절차는 가장 높은 점수 매트릭스 셀에서 시작하여 점수가 0인 셀이 마주칠 때까지 진행되며 가장 높은 점수 매트릭스 로컬 정렬을 제공한다. 시공간에서의 2차적 복잡성 때문에, 그것은 종종 대규모 문제에 실질적으로 적용될 수 없고, 덜 일반적이지만 더 계산적으로 더 효율적인 대안인 (Gotoh, 1982),^[2] (Altschul and Erickson, 1986), ^[3](Myers and Miller, 1988)을 위해 대체된다.^[4]

역사

1970년, 사울 B. 니들맨과 크리스티안 D. Wunsch는 시퀀스 정렬을 위한 경험적 호몰로지 알고리즘을 제안했으며, Needleman--라고도 한다.운슈 알고리즘.^[5] $O(mn)$ $O(mn)$ ) $O(mn)$ 계산 $O(mn)$ 단계( $m$ $m$ 및 $n$ $n$ 은 $n$ 정렬되는 두 시퀀스의 길이)가 필요한 전역 정렬 알고리즘이다. 지구 정렬을 보여주기 위해 행렬의 반복 계산을 사용한다. 이후 10년 동안 산코프,^[6] 라이허트,^[7] 비이어^[8] 등은 유전자 시퀀스 분석을 위한 대체 휴리스틱 알고리즘을 공식화했다. 판매자는 시퀀스 거리 측정 시스템을 도입했다.^[9] 1976년에 Waterman 등은 원래 측정 시스템에 갭의 개념을 추가했다.^[10] 1981년에 스미스와 워터맨은 지역 정렬 계산을 위한 스미스-워터맨 알고리즘을 발표했다.

Smith-Waterman 알고리즘은 상당히 많은 시간을 요구하고 있다. 길이 $m$ $m$ 과 $m$ $n$ ${\displaystyle$ n $n$ $O(mn)$ $O(mn)$ ) $O(mn)$ 의 $O(mn)$ 두 시퀀스를 정렬하려면 시간이 필요하다. 고토와^[2] 알츠철은^[3] 알고리즘을 $O(mn)$ $O(mn)$ ) $O(mn)$ 단계로 $O(mn)$ 최적화했다. 공간 복잡성은 마이어스와 밀러가^[4] $O(mn)$ n $O(mn)$ ) $O(mn)$ 에서 $O(mn)$ $O(n)$ ${\displaystyle O(n)}($ 선형)까지 최적화했으며, 여기서 $n$ {\ $displaystyle n}$ 은 가능한 많은 최적 정렬 중 하나만 원하는 경우 짧은 시퀀스의 길이입니다 $n$ .

동기

최근 몇 년 동안 다양한 유기체를 대상으로 진행된 게놈 프로젝트는 유전자와 단백질의 방대한 양의 시퀀스 데이터를 생성했으며, 이를 위해서는 연산 분석이 필요하다. 염기서열 정렬은 유전자 또는 단백질 사이의 관계를 보여주며, 그들의 호몰로지 및 기능성을 더 잘 이해하게 한다. 시퀀스 정렬은 보존된 도메인과 모티브도 나타낼 수 있다.

국부적 정렬의 한 가지 동기는 멀리 연관되어 있는 생물학적 시퀀스 사이의 유사성이 낮은 지역에서 정확한 정렬을 얻는 어려움이다. 왜냐하면 돌연변이가 진화 시간에 걸쳐 너무 많은 '소음'을 더했기 때문에 그러한 영역의 의미 있는 비교가 가능하기 때문이다. 국지적 정렬은 그러한 영역을 완전히 피하고 양성 점수(즉, 진화적으로 보존된 유사성 신호를 가진 지역)에 초점을 맞춘다. 지역 맞춤을 위한 전제조건은 마이너스 기대 점수다. 기대 점수는 점수 체계(위헌 매트릭스 및 갭 페널티)가 무작위 시퀀스에 대해 산출할 평균 점수로 정의된다.

지역 맞춤을 사용하는 또 다른 동기는 최적의 지역 맞춤을 위한 신뢰할 수 있는 통계 모델(칼린과 알츠철에 의해 개발됨)이 있다는 것이다. 관련 없는 시퀀스의 정렬은 극단값 분포를 따르는 최적의 국소 정렬 점수를 산출하는 경향이 있다. 이 속성은 프로그램이 두 시퀀스의 최적 로컬 정렬에 대한 기대값을 산출할 수 있도록 하며, 이는 관련 없는 두 시퀀스가 관측 점수보다 크거나 같은 최적의 로컬 정렬을 얼마나 자주 산출하는지를 측정한 것이다. 매우 낮은 기대 값은 문제의 두 시퀀스가 공통 조상을 공유할 수 있다는 것을 의미하는 동음이의어일 수 있음을 나타낸다.

알고리즘.

스미스-워터맨 알고리즘 채점 방법

Let $A=a_{1}a_{2}...a_{n}$ = $A=a_{1}a_{2}...a_{n}$ $A=a_{1}a_{2}...a_{n}$ $A=a_{1}a_{2}...a_{n}$ . . $A=a_{1}a_{2}...a_{n}$ . $A=a_{1}a_{2}...a_{n}$ ${\$ }... $a_{n}}$ 와 $A=a_{1}a_{2}...a_{n}$ B $B=b_{1}b_{2}...b_{m}$ = $B=b_{1}b_{2}...b_{m}$ 1 $B=b_{1}b_{2}...b_{m}$ $B=b_{1}b_{2}...b_{m}$ . $B=b_{1}b_{2}...b_{m}$ . $B=b_{1}b_{2}...b_{m}$ $B=b_{1}b_{2}...b_{m}$ ${\$ $b_{m}}$ 은(는) 정렬할 시퀀스이며 $B=b_{1}b_{2}...b_{m}$ , $m$ 서 $n$ $n$ 과 $n$ $m$ $m$ 은(는) $A$ $B$ A $A$ 와 B ${\displaystystyle B}$ 의 길이입니다 $m$ .

대체 매트릭스와 간격 벌점 체계를 결정한다.
- $s(a,b)$ ( $s(a,b)$ , $s(a,b)$ ) $s(a,b)$ $s(a,b)$ - 두 시퀀스를 구성하는 요소의 유사성 점수
- $W_{k}$ $W_{k}$ ${\$ $W_{k}$ - 길이가 $k$ 인 간격의 벌칙 $k$
점수 매트릭스 $H$ ${\displaystyle$ H $}$ 을(를) 구성하고 첫 $H$ 번째 행과 첫 번째 열을 초기화하십시오. 점수 매트릭스의 크기는 (n $(n+1)*(m+1)$ + $(n+1)*(m+1)$ ) $(n+1)*(m+1)$ (m $(n+1)*(m+1)$ + $(n+1)*(m+1)$ $){\displaystyle (n+1)**(m+1)}$ 입니다 $(n+1)*(m+1)$ 매트릭스는 0 기반 인덱싱을 사용한다.
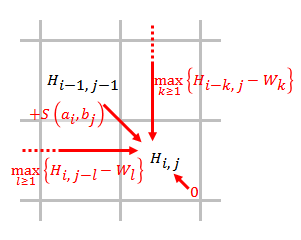
$H_{k0}=H_{0l}=0\quad for\leq k\leq n\quad and\quad 0\leq l\leq m$
아래 방정식을 사용하여 채점 매트릭스를 채우십시오.
$H_{ij}=\max {\begin{case}H_{i-1,j-1}+s(a_{i},b_{j}),\\\max _{k\geq 1}\{H_{i-k,j}-W_{k}\},\\\max _{l\geq 1}\{H_{i,j-l}-W_{l}\},\\0\end{cases}}\qquad (1\leq i\leq n,1\leq j\leq m)$

어디에

$H_{i-1,j-1}+s(a_{i},b_{j})$ $H_{i-1,j-1}+s(a_{i},b_{j})$ - $H_{i-1,j-1}+s(a_{i},b_{j})$ , $H_{i-1,j-1}+s(a_{i},b_{j})$ j - $H_{i-1,j-1}+s(a_{i},b_{j})$ + s $H_{i-1,j-1}+s(a_{i},b_{j})$ , $H_{i-1,j-1}+s(a_{i},b_{j})$ j $H_{i-1,j-1}+s(a_{i},b_{j})$ ) ${\displaystyle H_{i-1,j-1}+s(a_{i},b_{j}})$ 는 $a_{i}$ ${\$ 와 $a_{i}$ $b_{j}$ ${\$ 를 정렬하는 점수다 $H_{i-1,j-1}+s(a_{i},b_{j})$ $b_{j}$

$H_{i-k,j}-W_{k}$ $Hi$ $H_{i-k,j}-W_{k}$ - $H_{i-k,j}-W_{k}$ , j - $H_{i-k,j}-W_{k}$ k ${\$ $a_{i}$ ${\displaystyle a_$ ${i$ $}}}$ 의 간격 끝에 있는 $a_{i}$ 경우 점수 $H_{i-k,j}-W_{k}$ $k$

$H_{i,j-l}-W_{l}$ $b_{j}$ $H_{i,j-l}-W_{l}$ , $H_{i,j-l}-W_{l}$ - $H_{i,j-l}-W_{l}$ $H_{i,j-l}-W_{l}$ ${\$ l}}}{ $l}}$ 은(는) $b_{j}$ 길이 $l$ {\ $displaystyle$ $b_{j}$ b_{ $j$ $}$ 의 간격 끝에 있는 $b_{j}$ 점수다 $H_{i,j-l}-W_{l}$ $l$

$0$ $0$ 은(는) $a_{i}$ ${\$ 및 $a_{i}$ $b_{j}$ $b_{j}$ ${\$ 까지의 유사성이 없음을 의미한다 $0$ $b_{j}$
트레이스백. 스코어링 $매트릭스$ H $H$ 에서 가장 높은 점수로 시작하여 $H$ 0점인 매트릭스 셀에서 종료하며, 각 점수의 소스에 기초한 트레이스백은 최상의 로컬 정렬을 생성한다.

설명

Smith-Waterman 알고리즘은 일치/미스마치(대체, 삽입 및 삭제라고도 함)에 따라 두 시퀀스를 정렬한다. 삽입과 삭제 모두 대시로 대표되는 간격을 도입하는 작업이다. Smith-Waterman 알고리즘에는 다음과 같은 몇 가지 단계가 있다.

대체 매트릭스와 간격 벌점 체계를 결정한다. 대체 매트릭스는 각 쌍의 염기 또는 아미노산을 일치 또는 불일치에 대한 점수를 할당한다. 보통 경기는 긍정적인 점수를 얻는 반면, 불일치는 상대적으로 낮은 점수를 받는다. 갭 페널티 기능은 갭을 열거나 연장할 때 점수 비용을 결정한다. 사용자들은 목표에 따라 적절한 점수 체계를 선택할 것을 제안한다. 또한 대체 매트릭스와 갭 페널티를 서로 다른 조합으로 시도해 보는 것도 좋은 관행이다.
스코어링 매트릭스를 초기화하십시오. 채점 매트릭스의 치수는 각 시퀀스의 길이 1+이다. 첫 번째 행과 첫 번째 열의 모든 요소는 0으로 설정된다. 여분의 첫 번째 행과 첫 번째 열은 어떤 위치에서든 한 시퀀스를 다른 시퀀스에 정렬할 수 있게 하고, 이들을 0으로 설정하면 단자 간격이 패널티에서 자유로워진다.
득점. 대체(대각선 점수) 또는 간격 추가(수평 및 수직 점수)의 결과를 고려하여 매트릭스에서 각 요소를 왼쪽에서 오른쪽으로, 위에서 아래로 점수를 매긴다. 어느 점수도 양수가 되지 않으면 이 요소는 0을 얻는다. 그렇지 않으면 가장 높은 점수를 사용하고 그 점수의 출처를 기록한다.
트레이스백. 점수가 가장 높은 요소부터 시작하여 0이 발생할 때까지 각 점수의 출처를 재귀적으로 기준으로 추적한다. 주어진 채점제도에 근거하여 유사성 점수가 가장 높은 부문은 이 과정에서 생성된다. 두 번째로 가장 좋은 로컬 얼라인먼트를 얻으려면 가장 좋은 얼라인먼트의 트레이스 밖에 있는 두 번째로 높은 점수에서 시작하는 트레이스백 프로세스를 적용하십시오.

니들맨과 비교운슈 알고리즘

전역 및 로컬 시퀀스 정렬

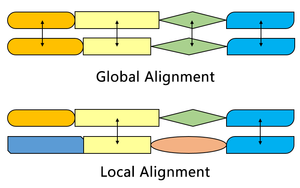
Smith-Waterman 알고리즘은 니들맨-과 유사한 두 시퀀스에서 세그먼트를 찾는다.Wunsch 알고리즘은 두 개의 완전한 시퀀스를 정렬한다. 그러므로, 그들은 다른 목적을 위해 봉사한다. 두 알고리즘 모두 대체 매트릭스, 갭 페널티 함수, 점수 매트릭스, 트레이스백 프로세스의 개념을 사용한다. 세 가지 주요 차이점은 다음과 같다.

	스미스-워터맨 알고리즘	니들먼-운슈 알고리즘
초기화	첫 번째 행과 첫 번째 열이 0으로 설정됨	첫 번째 행과 첫 번째 열은 갭 페널티가 부과된다.
점수 매기기	음수 점수가 0으로 설정됨	점수는 음수일 수 있다.
트레이스백.	가장 높은 점수로 시작하여 0이 발견되면 종료	행렬의 오른쪽 아래에 있는 셀부터 시작하여 왼쪽 상단 셀까지

가장 중요한 차별점 중 하나는 스미스-워터맨 알고리즘의 점수 체계에서 음수가 할당되지 않아 국소 정렬이 가능하다는 점이다. 어떤 요소가 0보다 낮은 점수를 갖는 경우, 이 위치까지의 시퀀스는 유사성이 없다는 것을 의미한다. 그런 다음 이 요소는 이전 정렬에서 영향을 제거하기 위해 0으로 설정될 것이다. 이런 식으로 계산은 그 후의 어느 위치에서나 계속 정렬을 찾을 수 있다.

Smith-Waterman 알고리즘의 초기 점수 매트릭스는 한 시퀀스의 어떤 세그먼트를 다른 시퀀스의 임의 위치에 정렬할 수 있게 한다. 인 니들먼-그러나 전체 시퀀스를 정렬하기 위해서는 엔드 갭 페널티도 고려해야 한다.

대체 행렬

각 염기 치환 또는 아미노산 치환에는 점수가 할당된다. 일반적으로 경기에는 긍정적인 점수가 할당되고, 미스매치에는 상대적으로 낮은 점수가 할당된다. DNA 서열을 예로 들어보자. 일치가 +1, 불일치가 -1이면 대체 행렬은 다음과 같다.

	A	G	C	T
A	1	-1	-1	-1
G	-1	1	-1	-1
C	-1	-1	1	-1
T	-1	-1	-1	1

This substitution matrix can be described as: $s(a_{i},b_{j})={\begin{cases}+1,\quad a_{i}=b_{j}\\-1,\quad a_{i}\neq b_{j}\end{cases}}$

염기 대체나 아미노산 대체는 점수가 다를 수 있다. 아미노산의 대체 매트릭스는 보통 베이스보다 더 복잡하다. PAM, BlOSUM을 참조하십시오.

갭 페널티

갭 벌칙은 삽입 또는 삭제 점수를 지정한다. 단순 갭 페널티 전략은 갭마다 고정 점수를 사용하는 것이다. 그러나 생물학에서는 현실적인 이유로 점수를 다르게 따질 필요가 있다. 한편으로, 두 시퀀스 사이의 부분적인 유사성은 공통적인 현상이다. 다른 한편으로, 하나의 유전자 돌연변이 사건은 하나의 긴 갭을 삽입하는 결과를 초래할 수 있다. 따라서, 긴 간격을 형성하는 연결된 간격은 일반적으로 여러 개의 흩어져 있는 짧은 간격보다 선호된다. 이러한 차이를 감안하기 위해 점수 체계에 갭 오프닝과 갭 연장 개념을 추가했다. 보통 갭 확장 점수보다 갭 확장 점수가 높다. 예를 들어, EMBOSS Water의 기본 매개변수는 갭 개방 = 10, 갭 확장 = 0.5이다.

여기서 우리는 갭 페널티를 위한 두 가지 일반적인 전략을 논한다. 자세한 전략은 갭 페널티를 참조하십시오. $W_{k}$ $W_{k}$ ${\$ 을 $k$ 를) 길이 $W_{k}$ $k$ $k$ 의 갭 벌칙 함수로 한다.

선형

선형 갭 페널티 함수를 사용할 때 Simplified Smith-Waterman 알고리즘

선형 갭 벌칙은 갭을 열고 연장할 때 동일한 점수를 갖는다.

$W_{k}=kW_{1}$ $W_{k}=kW_{1}$ = $W_{k}=kW_{1}$ $W_{k}=kW_{1}$ $W_{k}=kW_{1}$ ${\$

여기서 $W_{1}$ $W_{1}$ ${\$ }는 단일 간격의 비용이다 $W_{1}$ .

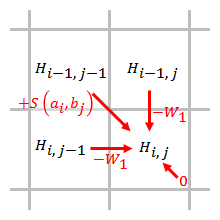
갭 벌칙은 갭 길이에 정비례한다. 선형 갭 페널티를 사용할 경우 Smith-Waterman 알고리즘을 다음과 같이 단순화할 수 있다.

$H_{ij}=\max {\begin{case}H_{i-1,j-1}+s(a_{i},b_{j}),\\H_{i-1,j}-W_{1},\H_{i,j-1}-{1},\0\end{case}}}}}$

단순화된 알고리즘은 $O(mn)$ ( $O(mn)$ n $O(mn)$ ) $O(mn)$ 단계를 $O(mn)$ 사용한다. 요소를 채점할 때는 이 요소에 직접 인접한 요소로부터의 갭 페널티만 고려할 필요가 있다.

아핀

갭 벌칙은 갭 개방과 확장을 별도로 고려한다.

$W_{k}=uk+v\quad (u>0,v>0)$ $W_{k}=uk+v\quad (u>0,v>0)$ = $W_{k}=uk+v\quad (u>0,v>0)$ + $W_{k}=uk+v\quad (u>0,v>0)$ > $W_{k}=uk+v\quad (u>0,v>0)$ , $W_{k}=uk+v\quad (u>0,v>0)$ v $W_{k}=uk+v\quad (u>0,v>0)$ > $W_{k}=uk+v\quad (u>0,v>0)$ ) ${\displaystyle W_{k}=uk+v\quad$ (u $>0,v$ > $0$

여기서 $v$ $v$ 은 $v$ (는) 갭 개방 패널티, $u$ ${\displaystyle$ u}은 $($ 는 $u$ ) 갭 확장 패널티다. 예를 들어 길이 2의 간격에 대한 벌칙은 2 $2u+v$ + $2u+v$ $2u+v$ 입니다 $2u+v$

원래의 스미스-워터맨 알고리즘 논문에는 임의의 갭 페널티가 사용되었다. $O(m^{2}n)$ ( $O(m^{2}n)$ $O(m^{2}n)$ ) $O(m^{2}n)$ 단계를 $O(m^{2}n)$ 사용하므로 시간이 상당히 많이 소요된다. 고토흐는 아핀 갭 페널티 단계를 $O(mn)$ ( $O(mn)$ n $O(mn)$ ) $O(mn)$ ^[2]로 최적화했지만, 최적화된 알고리즘은 하나의 최적 정렬만 찾으려 할 뿐, 최적의 정렬은 보장되지 않는다.^[3] 알츠철은 계산 복잡성을 유지하면서 모든 최적 맞춤을 찾기 위해 고토의 알고리즘을 수정했다.^[3] 이후 마이어스와 밀러는 고토와 알츠철의 알고리즘을 1975년 허쉬버그가 발표한 방법에 따라 더욱 수정할 수 있다고 지적하고 이 방법을 적용했다.^[11]^[4] 마이어스와 밀러의 알고리즘은 $O(n)$ ) $O(n)$ 공간을 $O(n)$ 사용하여 두 시퀀스를 정렬할 수 있으며, $n$ $n$ 은(는) 더 짧은 시퀀스의 길이가 된다 $n$ .

갭 페널티 예

시퀀스 정렬 수행 TACGGCCCCTAC 및 TAGCCCTCGTCA를 예로 들 수 있다. 선형 갭 페널티 함수를 사용하면 (EMBOSS Water가 수행하는 조정) 결과가 된다. 대체 매트릭스는 DNA가 가득 차 있다. 갭 개방 및 연장 모두 1.0:

TACGGCCCGCTA-C  TA--G-CC-CTATC

Affine 갭 페널티를 사용할 경우 결과는 다음과 같다(갭 개방 및 확장은 각각 5.0, 1.0).

TACGGCCCGCTA  TA--GCC-CTA

이 예는 가혹한 간격 벌점이 흩어져 있는 작은 간격을 피하는 데 도움이 된다는 것을 보여준다.

점수 매트릭스

채점 매트릭스의 기능은 두 시퀀스로 모든 성분 간에 일대일 비교를 실시하고 최적 정렬 결과를 기록하는 것이다. 채점 과정은 동적 프로그래밍의 개념을 반영한다. 최종 최적 맞춤은 반복적으로 증가하는 최적 맞춤에 의해 발견된다. 즉, 어떤 경로(일치/미스매치 또는 삽입 간격)가 이전의 최적 정렬에서 가장 높은 점수를 주는지를 결정함으로써 현재의 최적 정렬이 생성된다. 행렬의 크기는 한 시퀀스 길이 + 다른 시퀀스 길이 + 1이다. 추가 첫 번째 행과 첫 번째 열은 한 시퀀스를 다른 시퀀스의 어떤 위치에 정렬하는 것을 목적으로 한다. 첫 번째 줄과 첫 번째 열은 모두 0으로 설정하여 끝 갭이 불이익을 받지 않도록 한다. 초기 점수 매트릭스는 다음과 같다.

		b₁	…	b_j	…	b_m
	0	0	…	0	…	0
a의₁	0
…	…
a의_i	0
…	…
a의_n	0

예

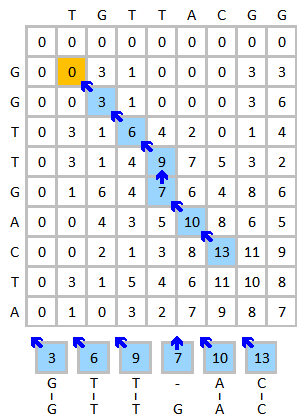
DNA 시퀀스 TGTTACGG와 GGTTGA의 정렬을 예로 들어보자. 다음 구성표를 사용하십시오.

대체 행렬: $s(a_{i},b_{j})={\begin{cases}+3,\quad a_{i}=b_{j}\\-3,\quad a_{i}\neq b_{j}\end{cases}}$ ( i $s(a_{i},b_{j})={\begin{cases}+3,\quad a_{i}=b_{j}\\-3,\quad a_{i}\neq b_{j}\end{cases}}$ , $s(a_{i},b_{j})={\begin{cases}+3,\quad a_{i}=b_{j}\\-3,\quad a_{i}\neq b_{j}\end{cases}}$ $s(a_{i},b_{j})={\begin{cases}+3,\quad a_{i}=b_{j}\\-3,\quad a_{i}\neq b_{j}\end{cases}}$ ) $s(a_{i},b_{j})={\begin{cases}+3,\quad a_{i}=b_{j}\\-3,\quad a_{i}\neq b_{j}\end{cases}}$ = $s(a_{i},b_{j})={\begin{cases}+3,\quad a_{i}=b_{j}\\-3,\quad a_{i}\neq b_{j}\end{cases}}$ { $s(a_{i},b_{j})={\begin{cases}+3,\quad a_{i}=b_{j}\\-3,\quad a_{i}\neq b_{j}\end{cases}}$ + $s(a_{i},b_{j})={\begin{cases}+3,\quad a_{i}=b_{j}\\-3,\quad a_{i}\neq b_{j}\end{cases}}$ , $s(a_{i},b_{j})={\begin{cases}+3,\quad a_{i}=b_{j}\\-3,\quad a_{i}\neq b_{j}\end{cases}}$ = $s(a_{i},b_{j})={\begin{cases}+3,\quad a_{i}=b_{j}\\-3,\quad a_{i}\neq b_{j}\end{cases}}$ j $s(a_{i},b_{j})={\begin{cases}+3,\quad a_{i}=b_{j}\\-3,\quad a_{i}\neq b_{j}\end{cases}}$ - 3, $s(a_{i},b_{j})={\begin{cases}+3,\quad a_{i}=b_{j}\\-3,\quad a_{i}\neq b_{j}\end{cases}}$ $s(a_{i},b_{j})={\begin{cases}+3,\quad a_{i}=b_{j}\\-3,\quad a_{i}\neq b_{j}\end{cases}}$ $s(a_{i},b_{j})={\begin{cases}+3,\quad a_{i}=b_{j}\\-3,\quad a_{i}\neq b_{j}\end{cases}}$ $s(a_{i},b_{j})={\begin{cases}+3,\quad a_{i}=b_{j}\\-3,\quad a_{i}\neq b_{j}\end{cases}}$ $displaystyle s(a_{i},b_{j}}={j$ }}}={\ $gin}+3,\quad a_{i}={j}\-3,\quad a_{i}\neq$ }\{ $j}end}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$
갭 페널티: $W_{k}=2k$ k $W_{k}=2k$ = $W_{k}=2k$ $W_{k}=2k$ ${\displaystyle W_{k}=2k}($ $W_{1}=2$ 1 $W_{1}=2$ = $W_{1}=2$ $W_{1}=2$ 의 선형 갭 페널티 $W_{1}=2$

아래와 같이 채점 매트릭스를 초기화하여 채운다. 이 수치는 처음 3개 요소의 득점 과정을 보여준다. 노란색은 고려되고 있는 베이스를 나타낸다. 빨간색은 점수가 매겨지는 셀에 대해 가능한 가장 높은 점수를 나타낸다.

채점 매트릭스 초기화(왼쪽 1) 및 처음 세 요소(왼쪽 2-4)의 채점 프로세스

완성된 채점 매트릭스는 왼쪽 아래에 표시되어 있다. 파란색은 가장 높은 점수를 보여준다. 요소는 둘 이상의 요소로부터 점수를 받을 수 있으며, 이 요소가 역추적될 경우 각각 다른 경로를 형성하게 된다. 최고 점수가 여러 개일 경우 각 최고 점수부터 추적 작업을 수행해야 한다. 트레이스백 과정은 오른쪽 아래에 나와 있다. 역방향으로 최적의 로컬 정렬이 생성된다.


채점 매트릭스 완료(최고점수는 파란색)	트레이스백 프로세스 및 정렬 결과

정렬 결과는 다음과 같다.

G T T - A C   G T T G A C

실행

Smith-Waterman 알고리즘, SSEARK의 구현은 UVA FASTA 다운로드의 FASTA 시퀀스 분석 패키지에서 이용할 수 있다. 이 구현에는 전력에 대한 Altivec 가속 코드가 포함됨Wozniak^[13], 1997년 접근법을 ^[12]수정하고 파라에 의해 개발된 SSE2 벡터화를 사용하여 최적의 단백질 시퀀스 데이터베이스 검색을 상당히 실용적으로 사용하여 비교 속도를 10배~20배 향상시키는 PC G4 및 G5 프로세서. 도서관 SSW는 최적의 Smith-Waterman 점수 외에도 맞춤 정보를 반환하도록 Farrar의 구현을 확장한다.^[14]

가속 버전

FPGA

크레이는 FPGA 칩을 기반으로 한 재구성 가능한 컴퓨팅 플랫폼을 사용하여 스미스-워터맨 알고리즘의 가속화를 시연했으며, 결과는 표준 마이크로프로세서 기반 솔루션보다 최대 28배 빠른 속도를 보였다. Smith-Waterman 알고리즘의 또 다른 FPGA 기반 버전은 2.2GHz Opteron 프로세서에 대해 FPGA(Virtex-4)의 속도가 최대 100배^[15] 향상되는 것을 보여준다.^[16] TimeLogic DeCyper와 CodeQuest 시스템도 PCIe FPGA 카드를 사용하여 Smith-Waterman과 Framesearch를 가속화한다.

2011년 석사학위 논문에는 FPGA 기반 Smith-Waterman 가속도의 분석이 포함되어 있다.

Xilinx SDAcel로 컴파일된 2016년 간행물 OpenCL 코드는 게놈 염기서열을 가속화하고 CPU/GPU 성능/W를 12-21배 능가하며 매우 효율적인 구현이 제시되었다. Xilinx Virtex-7 2000T FPGA가 장착된 PCIe FPGA 카드 1장을 사용했을 때 와트당 성능은 CPU/GPU보다 12~21배 향상됐다.

GPU

로렌스 리버모어 국립 연구소와 미국 에너지부 공동 게놈 연구소는 그래픽 처리 장치(GPU)를 사용하여 Smith-Waterman 로컬 시퀀스 정렬 검색의 가속 버전을 구현했으며, 예비 결과는 소프트웨어 구현에 비해 2배 빠른 속도를 보였다.^[18] 바이오파셋 소프트웨어에서도 1997년부터 비슷한 방식이 이미 구현돼 동일한 속도상승 요인으로 작용하고 있다.^[19]

NVIDIA의 CUDA C 플랫폼에서 알고리즘의 여러 GPU 구현도 이용할 수 있다.^[20] 파라르가 가장 잘 알려진 CPU 구현(x86 아키텍처의 SIMD 지침 사용)과 비교했을 때, 단일 NVidia GeForce 8800 GTX 카드를 사용한 이 솔루션의 성능 테스트에서는 작은 시퀀스에서는 성능이 약간 증가하지만 큰 시퀀스에서는 성능이 약간 떨어지는 것으로 나타났다. 그러나 이중 NVidia GeForce 8800 GTX 카드에서 실행되는 동일한 테스트는 모든 시퀀스 크기에 대해 Farrar 구현보다 거의 두 배 빠르다.

이전 버전보다 빠르고 쿼리 길이에 대한 제약도 없앤 새로운 GPU CUDA SW 구현이 현재 이용 가능하다. CUDASW++를 참조하십시오.

CUDA에 대한 11가지 SW 구현이 보고되었으며, 그 중 3개는 30X의 속도 향상을 보고한다.^[21]

심드

2000년에, Intel Pentium MMX 프로세서에서 이용 가능한 단일 명령, 다중 데이터(SIMD) 기술 및 유사한 기술을 사용한 Smith-Waterman 알고리즘의 빠른 구현이 Rognes와 Seeberg의 간행물에 설명되었다.^[22] Wozniak(1997) 접근방식과 대조적으로, 새로운 구현은 대각선 벡터가 아닌 질의 순서와 평행한 벡터에 기초했다. Sensl Bio informatics사는 이 접근법을 다루는 특허를 출원했다. Sensl은 소프트웨어를 추가로 개발하고 있으며 학술용 실행 파일을 무료로 제공하고 있다.

SSE2 확장 기능을 갖춘 Intel/AMD 프로세서에 8-16배 속도를 제공하는 알고리즘의 SSE2 벡터화(Farrar, 2007)가 현재 이용 가능하다.^[13] 코어 마이크로아키텍처를 사용하여 Intel 프로세서에서 실행될 경우 SSE2 구현은 20배 증가를 달성한다. Farrar의 SSE2 구현은 FASTA 시퀀스 비교 패키지의 SSEARK 프로그램으로 이용할 수 있다. SSEARCH는 유럽 생물정보학 협회의 유사성 검색 프로그램에 포함되어 있다.

공개된 백서에 따르면 덴마크 생물정보학 회사 CLC bio는 인텔 2.17GHz 코어 2 듀오 CPU에서 SSE2로 표준 소프트웨어 구현 속도보다 200배 가까이 빠른 속도를 달성했다.

Intel 및 AMD(Advanced Micro Devices) 기반 리눅스 서버에 있는 Smith-Waterman 알고리즘의 가속 버전은 바이오 셀렉션이 제공하는 GenCore 6 패키지가 지원한다. 이 소프트웨어 패키지의 성능 벤치마크는 동일한 프로세서에서 표준 소프트웨어 구현에 비해 최대 10배 빠른 가속을 보여 준다.

현재 생명정보학 분야에서 유일하게 스미스-워터맨을 가속화하는 SSE와 FPGA 솔루션을 모두 제공하는 CLC 바이오정보학 큐브를 통해 표준 소프트웨어 구현에 비해 110개 이상의 속도를 달성했다.^{[citation needed]}

SSSE3가 탑재된 CPU에 알고리즘을 가장 빨리 구현하는 것은 GNU 아페로 일반 공중 라이선스(GNU Affero General Public License)에 따라 이용할 수 있는 SWIPE 소프트웨어(Rognes, 2011)를 찾을 수 있다.^[23] 병렬로, 이 소프트웨어는 16개의 다른 데이터베이스 시퀀스의 잔여물을 하나의 쿼리 잔여물과 비교한다. 375개의 잔여 쿼리 시퀀스를 사용하여 초당 1060억 개의 셀 업데이트 속도(GCUPS)가 이중 Intel Xeon X5650 6코어 프로세서 시스템에서 달성되었으며, 이는 Farrar의 '스트라이핑된' 접근법에 기초한 소프트웨어보다 6배 이상 빠른 속도다. BLOSUM50 매트릭스를 사용할 때 블라스트보다 빠르다.

C와 C++에서 대각선이라는 Smith-Waterman의 구현은 SIMD 명령 집합(x86 플랫폼의 경우 SSE4.1, PowerPC 플랫폼의 경우 AltiVec)을 사용한다. 오픈소스 MIT 라이선스로 발매된다.

셀 광대역 엔진

2008년, Farrar는^[24] Cell Broadband Engine에 대한 Stripple Smith-Waterman의^[13] 포트를 설명하고 IBM QS20 블레이드와 Sony PlayStation 3에 각각 32 및 12GCUPS의 속도를 보고했다.

제한 사항

유전자 데이터의 빠른 확장은 현재의 DNA 시퀀스 정렬 알고리즘의 속도에 도전한다. DNA 변종 발견을 위한 효율적이고 정확한 방법에 대한 필수적인 요구는 실시간 병렬 처리를 위한 혁신적인 접근법을 요구한다. 광학 컴퓨팅 접근방식은 현재의 전기 구현에 대한 유망한 대안으로 제시되어 왔다. OptCAM은 그러한 접근법의 한 예로서 스미스-워터맨 알고리즘보다 더 빠른 것으로 나타난다.^[25]

참고 항목

참조

^ Smith, Temple F. & Waterman, Michael S. (1981). "Identification of Common Molecular Subsequences" (PDF). Journal of Molecular Biology. 147 (1): 195–197. CiteSeerX 10.1.1.63.2897. doi:10.1016/0022-2836(81)90087-5. PMID 7265238.
^ ^a ^b ^c Osamu Gotoh (1982). "An improved algorithm for matching biological sequences". Journal of Molecular Biology. 162 (3): 705–708. CiteSeerX 10.1.1.204.203. doi:10.1016/0022-2836(82)90398-9. PMID 7166760.
^ ^a ^b ^c ^d Stephen F. Altschul & Bruce W. Erickson (1986). "Optimal sequence alignment using affine gap costs". Bulletin of Mathematical Biology. 48 (5–6): 603–616. doi:10.1007/BF02462326. PMID 3580642. S2CID 189889143.
^ ^a ^b ^c Miller, Webb; Myers, Eugene (1988). "Optimal alignments in linear space". Bioinformatics. 4 (1): 11–17. CiteSeerX 10.1.1.107.6989. doi:10.1093/bioinformatics/4.1.11. PMID 3382986.
^ Saul B. Needleman; Christian D. Wunsch (1970). "A general method applicable to the search for similarities in the amino acid sequence of two proteins". Journal of Molecular Biology. 48 (3): 443–453. doi:10.1016/0022-2836(70)90057-4. PMID 5420325.
^ Sankoff D. (1972). "Matching Sequences under Deletion/Insertion Constraints". Proceedings of the National Academy of Sciences of the United States of America. 69 (1): 4–6. Bibcode:1972PNAS...69....4S. doi:10.1073/pnas.69.1.4. PMC 427531. PMID 4500555.
^ Thomas A. Reichert; Donald N. Cohen; Andrew K.C. Wong (1973). "An application of information theory to genetic mutations and the matching of polypeptide sequences". Journal of Theoretical Biology. 42 (2): 245–261. Bibcode:1973JThBi..42..245R. doi:10.1016/0022-5193(73)90088-X. PMID 4762954.
^ William A. Beyer, Myron L. Stein, Temple F. Smith, and Stanislaw M. Ulam (1974). "A molecular sequence metric and evolutionary trees". Mathematical Biosciences. 19 (1–2): 9–25. doi:10.1016/0025-5564(74)90028-5.CS1 maint: 여러 이름: 작성자 목록(링크)
^ Peter H. Sellers (1974). "On the Theory and Computation of Evolutionary Distances". Journal of Applied Mathematics. 26 (4): 787–793. doi:10.1137/0126070.
^ M.S Waterman; T.F Smith; W.A Beyer (1976). "Some biological sequence metrics". Advances in Mathematics. 20 (3): 367–387. doi:10.1016/0001-8708(76)90202-4.
^ D. S. Hirschberg (1975). "A linear space algorithm for computing maximal common subsequences". Communications of the ACM. 18 (6): 341–343. CiteSeerX 10.1.1.348.4774. doi:10.1145/360825.360861. S2CID 207694727.
^ Wozniak, Andrzej (1997). "Using video-oriented instructions to speed up sequence comparison". Computer Applications in the Biosciences. 13 (2): 145–50. doi:10.1093/bioinformatics/13.2.145. PMID 9146961.
^ ^a ^b ^c Farrar, Michael S. (2007). "Striped Smith–Waterman speeds database searches six times over other SIMD implementations". Bioinformatics. 23 (2): 156–161. doi:10.1093/bioinformatics/btl582. PMID 17110365.
^ Zhao, Mengyao; Lee, Wan-Ping; Garrison, Erik P; Marth, Gabor T (4 December 2013). "SSW Library: An SIMD Smith-Waterman C/C++ Library for Use in Genomic Applications". PLOS ONE. 8 (12): e82138. arXiv:1208.6350. Bibcode:2013PLoSO...882138Z. doi:10.1371/journal.pone.0082138. PMC 3852983. PMID 24324759.
^ FPGA100x 서류:"복사본 Archived"(PDF).2008-07-05에 있는 원본(PDF)에서 Archived.2007-10-17 Retrieved.CS1 maint:제목(링크),"복사본 Archived"(PDF)로 보관 시 복사본입니다.2008-07-05에 있는 원본(PDF)에서 Archived.2007-10-17 Retrieved.CS1 maint:제목(링크)로 보관 시 복사, 그리고"복사본 Archived"(PDF).2011-07-20에 있는 원본(PDF)에서 Archived.2007-10-17 Retrieved.CS1 maint:제목(링크)로 보관 시 복사본입니다.
^ 프로게닉 프테 Ltd. "백서 - 컴퓨팅 워크플로우에서 병목현상을 제거하기 위한 10배~50배 빠른 속도로 집약적인 애플리케이션 가속화"
^ Vermij, Erik (2011). Genetic sequence alignment on a supercomputing platform (PDF) (M.Sc. thesis). Delft University of Technology. Archived from the original (PDF) on 2011-09-30. Retrieved 2011-08-17.
^ Liu, Yang; Huang, Wayne; Johnson, John; Vaidya, Sheila (2006). GPU Accelerated Smith–Waterman. Lecture Notes in Computer Science. 3994. SpringerLink. pp. 188–195. doi:10.1007/11758549_29. ISBN 978-3-540-34385-1.
^ "Bioinformatics High Throughput Sequence Search and Analysis (white paper)". GenomeQuest. Archived from the original on May 13, 2008. Retrieved 2008-05-09.
^ Manavski, Svetlin A. & Valle, Giorgio (2008). "CUDA compatible GPU cards as efficient hardware accelerators for Smith–Waterman sequence alignment". BMC Bioinformatics. 9 (Suppl 2:S10): S10. doi:10.1186/1471-2105-9-S2-S10. PMC 2323659. PMID 18387198.
^ "CUDA Zone". Nvidia. Retrieved 2010-02-25.
^ Rognes, Torbjørn; Seeberg, Erling (2000). "Six-fold speed-up of Smith–Waterman sequence database searches using parallel processing on common microprocessors". Bioinformatics. 16 (8): 699–706. doi:10.1093/bioinformatics/16.8.699. PMID 11099256.
^ Rognes, Torbjørn (2011). "Faster Smith–Waterman database searches with inter-sequence SIMD parallelisation". BMC Bioinformatics. 12: 221. doi:10.1186/1471-2105-12-221. PMC 3120707. PMID 21631914.
^ Farrar, Michael S. (2008). "Optimizing Smith–Waterman for the Cell Broadband Engine". Archived from the original on 2012-02-12. Cite 저널은 필요로 한다. journal= (도움말)
^ Maleki, Ehsan; Koohi, Somayyeh; Kavehvash, Zahra; Mashaghi, Alireza (2020). "OptCAM: An ultra‐fast all‐optical architecture for DNA variant discovery". Journal of Biophotonics. 13 (1): e201900227. doi:10.1002/jbio.201900227. PMID 31397961.

외부 링크

JAligner - Smith-Waterman 알고리즘의 오픈 소스 Java 구현
B.A.B.A. — 알고리즘을 시각적으로 설명하는 애플릿(소스 포함)
FASTA/SSearch — EBI의 서비스 페이지
UGENE Smith-Waterman 플러그인 — C++로 작성된 그래픽 인터페이스를 통해 알고리즘의 오픈 소스 SSEARCH 호환 구현
OPAL — 대규모 최적 시퀀스 정렬을 위한 SIMD C/C++ 라이브러리
대각선 — MIT 라이센스에 따라 SIMD 명령 집합(예: SSE4.1)이 포함된 오픈 소스 C/C++ 구현
SSW - MIT 라이센스에 따라 Smith-Waterman 알고리즘의 SIMD 구현에 API를 제공하는 오픈 소스 C++ 라이브러리
멜로디 시퀀스 정렬 - 멜로디 시퀀스 정렬을 위한 자바스크립트 구현
DRAGMAP Illumina DRAGEN FPGA 구현의 C++ 포트

[Smith1981-1] Smith, Temple F. & Waterman, Michael S. (1981). "Identification of Common Molecular Subsequences" (PDF). Journal of Molecular Biology. 147 (1): 195–197. CiteSeerX 10.1.1.63.2897. doi:10.1016/0022-2836(81)90087-5. PMID 7265238.

[Gotoh1982-2] Osamu Gotoh (1982). "An improved algorithm for matching biological sequences". Journal of Molecular Biology. 162 (3): 705–708. CiteSeerX 10.1.1.204.203. doi:10.1016/0022-2836(82)90398-9. PMID 7166760.

[Altschul1986-3] Stephen F. Altschul & Bruce W. Erickson (1986). "Optimal sequence alignment using affine gap costs". Bulletin of Mathematical Biology. 48 (5–6): 603–616. doi:10.1007/BF02462326. PMID 3580642. S2CID 189889143.

[Myers1988-4] Miller, Webb; Myers, Eugene (1988). "Optimal alignments in linear space". Bioinformatics. 4 (1): 11–17. CiteSeerX 10.1.1.107.6989. doi:10.1093/bioinformatics/4.1.11. PMID 3382986.

[Needleman1970-5] Saul B. Needleman; Christian D. Wunsch (1970). "A general method applicable to the search for similarities in the amino acid sequence of two proteins". Journal of Molecular Biology. 48 (3): 443–453. doi:10.1016/0022-2836(70)90057-4. PMID 5420325.

[Sankoff1972-6] Sankoff D. (1972). "Matching Sequences under Deletion/Insertion Constraints". Proceedings of the National Academy of Sciences of the United States of America. 69 (1): 4–6. Bibcode:1972PNAS...69....4S. doi:10.1073/pnas.69.1.4. PMC 427531. PMID 4500555.

[Reichert1973-7] Thomas A. Reichert; Donald N. Cohen; Andrew K.C. Wong (1973). "An application of information theory to genetic mutations and the matching of polypeptide sequences". Journal of Theoretical Biology. 42 (2): 245–261. Bibcode:1973JThBi..42..245R. doi:10.1016/0022-5193(73)90088-X. PMID 4762954.

[Beyer1974-8] William A. Beyer, Myron L. Stein, Temple F. Smith, and Stanislaw M. Ulam (1974). "A molecular sequence metric and evolutionary trees". Mathematical Biosciences. 19 (1–2): 9–25. doi:10.1016/0025-5564(74)90028-5.CS1 maint: 여러 이름: 작성자 목록(링크)

[Sellers1974-9] Peter H. Sellers (1974). "On the Theory and Computation of Evolutionary Distances". Journal of Applied Mathematics. 26 (4): 787–793. doi:10.1137/0126070.

[Waterman1976-10] M.S Waterman; T.F Smith; W.A Beyer (1976). "Some biological sequence metrics". Advances in Mathematics. 20 (3): 367–387. doi:10.1016/0001-8708(76)90202-4.

[Hirschberg1975-11] D. S. Hirschberg (1975). "A linear space algorithm for computing maximal common subsequences". Communications of the ACM. 18 (6): 341–343. CiteSeerX 10.1.1.348.4774. doi:10.1145/360825.360861. S2CID 207694727.

[Wozniak1997-12] Wozniak, Andrzej (1997). "Using video-oriented instructions to speed up sequence comparison". Computer Applications in the Biosciences. 13 (2): 145–50. doi:10.1093/bioinformatics/13.2.145. PMID 9146961.

[Farrar2007-13] Farrar, Michael S. (2007). "Striped Smith–Waterman speeds database searches six times over other SIMD implementations". Bioinformatics. 23 (2): 156–161. doi:10.1093/bioinformatics/btl582. PMID 17110365.

[14] Zhao, Mengyao; Lee, Wan-Ping; Garrison, Erik P; Marth, Gabor T (4 December 2013). "SSW Library: An SIMD Smith-Waterman C/C++ Library for Use in Genomic Applications". PLOS ONE. 8 (12): e82138. arXiv:1208.6350. Bibcode:2013PLoSO...882138Z. doi:10.1371/journal.pone.0082138. PMC 3852983. PMID 24324759.

[15] FPGA100x 서류:"복사본 Archived"(PDF).2008-07-05에 있는 원본(PDF)에서 Archived.2007-10-17 Retrieved.CS1 maint:제목(링크),"복사본 Archived"(PDF)로 보관 시 복사본입니다.2008-07-05에 있는 원본(PDF)에서 Archived.2007-10-17 Retrieved.CS1 maint:제목(링크)로 보관 시 복사, 그리고"복사본 Archived"(PDF).2011-07-20에 있는 원본(PDF)에서 Archived.2007-10-17 Retrieved.CS1 maint:제목(링크)로 보관 시 복사본입니다.

[Progeniq-16] 프로게닉 프테 Ltd. "백서 - 컴퓨팅 워크플로우에서 병목현상을 제거하기 위한 10배~50배 빠른 속도로 집약적인 애플리케이션 가속화"

[Vermij2011-17] Vermij, Erik (2011). Genetic sequence alignment on a supercomputing platform (PDF) (M.Sc. thesis). Delft University of Technology. Archived from the original (PDF) on 2011-09-30. Retrieved 2011-08-17.

[18] Liu, Yang; Huang, Wayne; Johnson, John; Vaidya, Sheila (2006). GPU Accelerated Smith–Waterman. Lecture Notes in Computer Science. 3994. SpringerLink. pp. 188–195. doi:10.1007/11758549_29. ISBN 978-3-540-34385-1.

[19] "Bioinformatics High Throughput Sequence Search and Analysis (white paper)". GenomeQuest. Archived from the original on May 13, 2008. Retrieved 2008-05-09.

[Manavski2008-20] Manavski, Svetlin A. & Valle, Giorgio (2008). "CUDA compatible GPU cards as efficient hardware accelerators for Smith–Waterman sequence alignment". BMC Bioinformatics. 9 (Suppl 2:S10): S10. doi:10.1186/1471-2105-9-S2-S10. PMC 2323659. PMID 18387198.

[21] "CUDA Zone". Nvidia. Retrieved 2010-02-25.

[RognesSeeberg2000-22] Rognes, Torbjørn; Seeberg, Erling (2000). "Six-fold speed-up of Smith–Waterman sequence database searches using parallel processing on common microprocessors". Bioinformatics. 16 (8): 699–706. doi:10.1093/bioinformatics/16.8.699. PMID 11099256.

[Rognes2011-23] Rognes, Torbjørn (2011). "Faster Smith–Waterman database searches with inter-sequence SIMD parallelisation". BMC Bioinformatics. 12: 221. doi:10.1186/1471-2105-12-221. PMC 3120707. PMID 21631914.

[Farrar2008-24] Farrar, Michael S. (2008). "Optimizing Smith–Waterman for the Cell Broadband Engine". Archived from the original on 2012-02-12. Cite 저널은 필요로 한다. journal= (도움말)

[optcam-25] Maleki, Ehsan; Koohi, Somayyeh; Kavehvash, Zahra; Mashaghi, Alireza (2020). "OptCAM: An ultra‐fast all‐optical architecture for DNA variant discovery". Journal of Biophotonics. 13 (1): e201900227. doi:10.1002/jbio.201900227. PMID 31397961.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[13]

[12]

[14]

[15]

[16]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

v t 생물정보학
데이터베이스	시퀀스 데이터베이스: GenBank, European Nucleotide Arch 보조 데이터베이스: UniProt, Swiss-Prot, TrEMBL, 단백질 정보 자원들을 함께 그룹화하는 단백질 시퀀스 데이터베이스 기타 데이터베이스: 단백질 데이터 뱅크, 앙상블 및 InterPro 전문 게놈 데이터베이스: BOLD, 사카로마이오스 게놈 데이터베이스, 플라이베이스, 벡터베이스, 웜베이스, 랫드 게놈 데이터베이스, PHI 기반, 아라비도시스 정보 자원 및 제브라피쉬 정보 네트워크
소프트웨어	블라스트 보타이 클라스탈 엠보스 흐머 근육 SAM도구 SOAP 제품군 톱햇
기타	서버: ExPASY 온톨로지: 진 온톨로지 로잘린드(교육 플랫폼)
기관	브로드 인스티튜트 중국 국가유전자은행(CNGB) 컴퓨터 생물학부(CBD) Microsoft Research - University of Trento Computing and Systems Biology(COSBI) DBCLS(Database Center for Life Science) 일본DBJ(DNA Data Bank of Japan 유럽생명정보연구소(EMBL-EBI) 유럽 분자생물연구소(EMBL) 플랫아이론 연구소 J. 크레이그 벤터 연구소(JCVI) 막스 플랑크 분자세포생물유전학연구소(MPI-CBG) 미국 국립 생명공학 정보 센터(NCBI) 일본유전학연구소 네덜란드 생물정보 센터(NBIC) 필리핀 게놈 센터(PGC) 스크립스 리서치 스위스 생물정보학 연구소(SIB) 웰컴 생어 연구소 화이트헤드 연구소
단체들	아프리카 생물정보학 전산생물학회(ASBCB) 오스트레일리아 생물정보자원(EMBL-AR) 유럽 분자생물학 네트워크(EMBnet) 국제 뉴클레오티드 시퀀스 데이터베이스 협업(INSDC) 국제 생물학 협회(ISB) 국제 컴퓨터 생물학 협회(ISCB) 학생회(ISCB-SC) 유전체학 및 통합 생물학 연구소(CSIR-IGIB) 일본 생물정보학회(JSBi)
회의	바젤 계산 생물학 회의 ([BC])² 유럽 전산 생물학 총회(ECCB) 분자생물학(ISMB)을 위한 지능형 시스템 국제 생물정보학회의(InCoB) ISCB 아프리카 ASBCB 생물정보학 회의 태평양 생물학 심포지엄(PSB) 컴퓨터 분자생물학 연구
파일 형식	CRAM 형식 FASTA 형식 FASTQ 형식 NeXML 형식 넥서스 형식 쌓기 형식 SAM 형식 스톡홀름 형식 VCF 형식
관련 항목	계산생물학 바이오뱅크의 목록 생물학적 데이터베이스 목록 분자유전학 시퀀싱 시퀀스 데이터베이스 시퀀스 정렬
카테고리 커먼스

v t 줄들
문자열 메트릭	대략적인 문자열 일치 비트맵 알고리즘 다메라우-레벤슈테인 거리 거리 편집 게슈탈트 패턴 매칭 해밍 거리 자로-윙클러 거리 리 거리 레벤슈테인 오토매틱 레벤슈테인 거리 바그너-피셔 알고리즘
문자열 검색 알고리즘	아포토리코-지안카를로 알고리즘 보이어-무어 문자열 검색 알고리즘 보이어-무어-호스풀 알고리즘 크누스-모리스-프라트 알고리즘 라빈-카프 알고리즘
다중 문자열 검색	아호코라식 코멘트-발터 알고리즘
정규식	정규 표현 엔진의 비교 정규문법 톰프슨의 건설 비결정론적 유한자동화
시퀀스 정렬	허슈베르크 알고리즘 니들먼-운슈 알고리즘 스미스-워터맨 알고리즘
데이터 구조	DAFSA 접미사 배열 자동 접미사 접미사 트리 일반화 접미사 트리 밧줄 3차 검색 트리 트라이
기타	파싱 패턴 매칭 압축 패턴 매칭 가장 긴 공통 부분 가장 긴 공통 하위 문자열 순차 패턴 마이닝 정렬

Search