서픽스 오토마톤

서픽스 오토마톤
서픽스 오토마톤
유형	서브스트링 인덱스
발명된	1983
발명자	앤셀름 블러머, 재닛 블러머, 안제이 에렌퓨흐트, 데이비드 하우슬러, 로스 매코넬
빅 O 표기의 시간 복잡도
알고리즘.
알고리즘.
공간

컴퓨터 과학에서 서픽스 오토마톤은 주어진 문자열의 서브스트링 인덱스를 나타내는 효율적인 데이터 구조이며, 모든 서브스트링에 대한 압축 정보의 저장, 처리 및 검색을 가능하게 한다. $문자열$ S의 접미사 오토마톤({ $displaystyle$ S})은 $S$ 초기 정점에서 최종 정점까지의 경로가 문자열의 접미사를 나타내도록 전용 초기 정점과 "최종" 정점 세트를 가진 최소 방향 비순환 그래프입니다.

오토마타 이론에서 접미사 오토마톤은 주어진 $S=s_{1}s_{2}\dots s_{n}$ S $S=s_{1}s_{2}\dots s_{n}$ $S=s_{1}s_{2}\dots s_{n}$ $S=s_{1}s_{2}\dots s_{n}$ $S=s_{1}s_{2}\dots s_{n}$ 2 $S=s_{1}s_{2}\dots s_{n}$ … $S=s_{1}s_{2}\dots s_{n}$ \ $displaystyle$ S $= s_{$ 1} $s_{2}\dots s_{n$ 의 접미사 집합을 인식하는 최소 부분 결정론적 유한 오토마톤이다.접미사 자동화의 상태 그래프는 DAWG(Directed acyclic word graph)라고 불리며, 결정론적 비순환적 유한 상태 자동화에 사용되기도 한다.

서픽스 오토마타는 1983년 덴버 대학과 콜로라도 볼더 대학의 과학자 그룹에 의해 도입되었다.이들은 선형 시간 온라인 알고리즘을 제안했으며 길이가 최소 2자 이상인 $문자열$ S $({displaystyle$ S})의 $S$ 서픽스 오토마톤은 ${\textstyle 2|S|-1}$ 2개의 $S-1$ ({ $textstyle$ 2 ${\textstyle 2|S|-1}$ $S-1})$ 상태와 ${\textstyle 3|S|-4}$ 3개의 ${\textstyle 3|S|-4}$ ({ $textstyle 3 S-4$ }) 전환이 ${\textstyle 3|S|-4}$ 있음을 보여주었다.추가 연구는 접미사 오토마타와 접미사 트리의 밀접한 관련성을 보여주었으며, 단일 발신 호를 가진 노드를 압축하여 얻은 압축 접미사 오토마톤과 같은 접미사 오토마타의 몇 가지 일반화를 개략적으로 설명했다.

서픽스 오토마타는 서브스트링 검색 및 2개 이상의 문자열로 이루어진 가장 큰 공통 서브스트링 계산과 같은 문제에 대한 효율적인 해결책을 제공합니다.

역사

스트링 abc와 abcab의 일반 CDAWG 도면을 사용한 Anselm Blumer

비록 비슷한 개념 초 접미사 나무들과 함께 피터 Weiner,[2]의 작품에서 연구되어 졌다 접미사 automaton의 개념 1983[1]의 과학자들의 덴버 대학교와 콜로라도 대학교 볼더의 집단에서 안젤름 블루머, 자넷 블루머, 안제이 Ehrenfeucht, 데이비드 Haussler과 로스 매코널로 구성된 도입되었는데, Vaughan^[3] 프랫과 아나톨 슬리센코.^[4]Blumer 등은 초기 작업에서 길이가1({ $displaystyle$ 1)보다 $1$ 큰 $2|S|-1$ S $({$ $displaystyle$ $S$ $})$ 에 $S$ $2|S|-1$ $3|S|-4$ 대해 작성된 접미사 오토마톤을 보여주었고 $,$ 자동화에 $대한 선형$ 알고리즘을 제안했다.온스트럭처링^[5]

1983년 Mu-Tian Chen과 Joel Seiferas는 독자적으로 Weiner의 1973년 서픽스 트리 구축^[2] 알고리즘에 ${\textstyle S^{R}}$ 문자열 ${\textstyle S^{R}}$ 의 ${\textstyle S^{R}}$ 서픽스 오토마톤(* $displaystyle$ S $^{R})$ 을 ${\textstyle S^{R}}$ 보조 ^[6]구조로 구축한다는 $S$ 것을 보여주었다.1987년, Blumer 등은 접미사 트리에 사용되는 압축 기술을 접미사 오토마톤에 적용하고 압축된 접미사 오토마톤을 발명했다. 이것은 또한 CDAWG(^[7]compacted directed acyclic word graph)라고도 불린다.1997년 Maxime Crochemore와 Renaud Vérin은 직접 CDAWG ^[1]구축을 위한 선형 알고리즘을 개발했습니다.2001년, 이네나가 슌스케 등은 트라이에 ^[8]의해 주어진 단어 세트에 대한 CDAWG 구축 알고리즘을 개발했다.

정의들

보통 접미사 오토마타와 관련 개념에 대해 말할 때, 특히 ^[9]다음과 같은 형식 언어 이론과 오토마타 이론의 몇 가지 개념이 사용됩니다.

알파벳은 단어 구성에 사용되는 유한 집합 $\Sigma$ δ(\ $displaystyle\Sigma)$ 입니다 $\Sigma$ .그 요소를 '문자'라고 한다.
"Word"는 문자 $\omega$ $\omega =\omega _{1}\omega _{2}\dots \omega _{n}$ $\omega =\omega _{1}\omega _{2}\dots \omega _{n}$ 1 $\omega =\omega _{1}\omega _{2}\dots \omega _{n}$ 2 ... $\omega =\omega _{1}\omega _{2}\dots \omega _{n}$ n { $displaystyle$ \ $opega$ _ ${$ 1} \ $obega$ _ {2} \ $\$ \ $obega _ {$ n} $\omega =\omega _{1}\omega _{2}\dots \omega _{n}$ 。 ${\$ { $displaystyle$ \ $}$ 의 $\omega$ "Length"는 $|\omega |=n$ { $displaystyle$ \ $|\omega |=n$ = $n$ }로 $표시$ 됩니다.
'포멀 랭귀지'는 주어진 알파벳 위에 있는 단어 집합이다.
"모든 단어의 언어"는 $(\$ 여기서 "*" 문자는 Kleene 별을 나타냄), "빈 단어"(길이가 0인 단어)는 $\varepsilon$ {\(\ $displaystyle \varepsilon$ 로 표시됩니다.
" $\alpha =\alpha _{1}\alpha _{2}\dots \alpha _{n}$ 연결" $\alpha =\alpha _{1}\alpha _{2}\dots \alpha _{n}$ $= α$ $\alpha =\alpha _{1}\alpha _{2}\dots \alpha _{n}$ $\alpha =\alpha _{1}\alpha _{2}\dots \alpha _{n}$ … $α$ n $\$ α _ { $1}\alpha _$ { $2}\alpha \alpha$ $\beta =\beta _{1}\beta _{2}\dots \beta _{m}$ { $\beta =\beta _{1}\beta _{2}\dots \beta _{m}$ } $\beta =\beta _{1}\beta _{2}\dots \beta _{m}$ $\beta =\beta _{1}\beta _{2}\dots \beta _{m}$ $\beta =\beta _{1}\beta _{2}\dots \beta _{m}$ $β$ 1 $\beta =\beta _{1}\beta _{2}\dots \beta _{m}$ 2 … $\beta =\beta _{1}\beta _{2}\dots \beta _{m}$ m _ {1 $}\$ alpha _ { $m}$ 은 $\beta =\beta _{1}\beta _{2}\dots \beta _{m}$ α $\alpha \cdot \beta$ \ $cdisplay$ style \ $alpha$ $=$ { $m}$ 로 $표시$ 된다.nds $\alpha$ α의 $\alpha$ 에 $\beta$ β {\ $displaystyle \alpha$ 로 $\beta$ 표기하여 얻은 단어, 즉 $\alpha \beta =\alpha _{1}\alpha _{2}\dots \alpha _{n}\beta _{1}\beta _{2}\dots \beta _{m}$ $\alpha \beta =\alpha _{1}\alpha _{2}\dots \alpha _{n}\beta _{1}\beta _{2}\dots \beta _{m}$ β $\alpha \beta =\alpha _{1}\alpha _{2}\dots \alpha _{n}\beta _{1}\beta _{2}\dots \beta _{m}$ $β$ $\alpha \beta =\alpha _{1}\alpha _{2}\dots \alpha _{n}\beta _{1}\beta _{2}\dots \beta _{m}$ $\alpha \beta =\alpha _{1}\alpha _{2}\dots \alpha _{n}\beta _{1}\beta _{2}\dots \beta _{m}$ … $\alpha \beta =\alpha _{1}\alpha _{2}\dots \alpha _{n}\beta _{1}\beta _{2}\dots \beta _{m}$ m ${\$ 1}\ $display$ \alpha _{{{\ $alpha$ } \alpha } _ ${{{{{\lang$ \lang} \alpha} \lang} $_$ {\langu}_{ $m}$ \lang}_{{\
"언어 연결" $(\displaystyle$ A $)$ 와 $A$ B(\ $displaystyle$ B $)$ 는 $B$ A $(\displaystyle$ A $\cdot$ B $)$ 또는 $A\cdot B$ $(\displaystyle$ AB $)$ 로 $AB$ 표시되며 쌍으로 연결된 $AB=\{\alpha \beta :\alpha \in A,\beta \in B\}$ $=$ { $AB=\{\alpha \beta :\alpha \in A,\beta \in B\}$ : $AB=\{\alpha \beta :\alpha \in A,\beta \in B\}$ α $AB=\{\alpha \beta :\alpha \in A,\beta \in B\}$ A $AB=\{\alpha \beta :\alpha \in A,\beta \in B\}$ display B(\ $displaystyle$ AB)에 해당합니다 $.$
단어 $\omega \in \Sigma ^{*}$ $\omega \in \Sigma ^{*}$ $σ$ $、$ \ $displaystyle \$ $\omega =\alpha \gamma \beta$ \ in \ Sigma $^$ { * } 、 $\omega =\alpha \gamma \beta$ 、 \ $display style$ \ sigma $=$ \ alpha \ $\omega =\alpha \gamma \beta$ $sigma$ $\omega =\alpha \gamma \beta$ , $\alpha ,\beta ,\gamma \in \Sigma ^{*}$ 、 $\alpha$ 、 $\alpha ,\beta ,\gamma \in \Sigma ^{*}$ $\alpha ,\beta ,\gamma \in \Sigma ^{*}$ 、 $\alpha ,\beta ,\gamma \in \Sigma ^{*}$ 、 , , $\alpha ,\beta ,\gamma \in \Sigma ^{*}$ \ $display$ style \ $alpha 、$ \ sigma 、 \ sigma $）$ α α α α α α α α α α α α α α α α α α α α α α 、 $、$ \ sigma 。 $e$ \displaystyle \mega $}$ 는 $\gamma$ $\omega$ ${\$ \ $displaystyle$ \ $mega }$ 의 $\omega$ "subword", "subword"(부호)로 불린다.
$T=T_{1}\dots Tn$ $T=T_{1}\dots Tn$ $T=T_{1}\dots Tn$ $T=T_{1}\dots Tn$ $T=T_{1}\dots Tn$ \ $displaystyle T$ $= T_{1}$ \ $dots Tn$ } $및$ $T_{l}T_{l+1}\dots T_{r}=S$ $T_{l}T_{l+1}\dots T_{r}=S$ + $T_{l}T_{l+1}\dots T_{r}=S$ ... $T_{l}T_{l+1}\dots T_{r}=S$ $=$ \ $display t_{l+1}$ \ $dots$ T_ ${$ $r$ } = $S$ $T_{l}T_{l+1}\dots T_{r}=S$ $（$ $1\leq l\leq r\leq n$ $l$ $1\leq l\leq r\leq n$ $l$ 서 l{ $displaystyle$ l $}$ 과 $l$ $r$ { $displaystyle$ r $r$ $}$ 은 T { $displaystyle$ T $}$ 에서 S {displaystyle S $}$ 의 $S$ $왼쪽$ 및 오른쪽 발생 위치라고 한다 $T$ .

오토마톤 구조

공식적으로는 결정론적 유한 오토마톤은 5 ${\mathcal {A}}=(\Sigma ,Q,q_{0},F,\delta )$ A $=$ ( ${\mathcal {A}}=(\Sigma ,Q,q_{0},F,\delta )$ ${\mathcal {A}}=(\Sigma ,Q,q_{0},F,\delta )$ , ${\mathcal {A}}=(\Sigma ,Q,q_{0},F,\delta )$ F ${\mathcal {A}}=(\Sigma ,Q,q_{0},F,\delta )$ $)$ (\ $displaystyle {$ A}}=(\ $Sigma,$ Q $,q_{0},F$ ,\delta ${\mathcal {A}}=(\Sigma ,Q,q_{0},F,\delta )$ 에 의해 결정된다.^[10]

$σ \$ $displaystyle$ \ $\Sigma$ Sigma $\Sigma$ }는 단어 구성에 사용되는 알파벳입니다.
$(\displaystyle$ Q $)$ 는 $Q$ 일련의 자동 "상태"입니다.
$q_{0}\in Q$ 0 $({displaystyle q_{$ 0}\ $in$ Q $)$ 는 $q_{0}\in Q$ 자동화의 "초기" 상태입니다.
$F\subset Q$ Q ( \ $displaystyle$ F \ $subset$ Q )는 $F\subset Q$ 자동화의 "최종" 상태의 집합입니다.
$Q$ $Q\times \Sigma \mapsto$ Q는 $\delta :Q\times \Sigma \mapsto Q$ 자동의 부분적인 " $전환$ " 함수입니다.이 경우 $\delta (q,\sigma )$ $Q$ , $\delta (q,\sigma )$ $display$ Q $,$ $σ$ σ q $q\in Q$ q display display ${\$ {\ σ display display display display $\delta (q,\sigma )$ $\sigma \in \Sigma$ display $q$ q q q qq q q {\ {\ {\ {\ {\ q $q$ q {\ {\ {\ {\ {\ {\ q {\ q q {\ {\ {\ {\ {\ q q q q q q q q q q q q q q q q q q $\delta (q,\sigma )$ $（$ \ $displaystyle \$ $\syslogs$ $\sigma$ 。

일반적으로 결정론적 유한 오토마톤은 다음과 같이 ^[10]유도 그래프("그림")로 표현된다.

그래프 꼭지점 세트는 $상태$ Q(\ $displaystyle$ Q $Q$ 에 대응합니다.
그래프에는 초기 $q_{0}$ $q_{0}$ 0 $({$ 에 대응하는 특정 마킹된 정점이 있습니다.
그래프에는 최종 $상태$ F $(\displaystyle$ F $F$ 에 대응하는 여러 개의 표시된 정점이 있습니다.
그래프 호 세트는 트랜지션 $\delta$ 인 $\delta$ \ $displaystyle \delta$ 에 대응합니다.
구체적으로는 ${\textstyle \delta (q_{1},\sigma )=q_{2}}$ 1 , ${\textstyle \delta (q_{1},\sigma )=q_{2}}$ ) $=$ 2 \ $textstyle \$ ( ( ( q $_ {1}$ , \ display $)=q_$ {2 $}}$ 는 ${\textstyle \delta (q_{1},\sigma )=q_{2}}$ $q_{1}$ $q_{2}$ ${\textstyle q_{1}{\begin{smallmatrix}{\sigma }\\[-5pt]{\longrightarrow }\end{smallmatrix}}q_{2}}$ $(\$ $displaystyle q_$ ${$ 1} )에서 $(\$ $displaystyle q_{2$ $\sigma$ 로 호가 표시됩니다.이 천이는 ${\textstyle q_{1}{\begin{smallmatrix}{\sigma }\\[-5pt]{\longrightarrow }\end{smallmatrix}}q_{2}}$ 로 ${\textstyle q_{1}{\begin{smallmatrix}{\sigma }\\[-5pt]{\longrightarrow }\end{smallmatrix}}q_{2}}$ 될 수도 있습니다 ${\textstyle q_{1}{\begin{smallmatrix}{\sigma }\\[-5pt]{\longrightarrow }\end{smallmatrix}}q_{2}}$ ${\textstyle q_{1}{\begin{smallmatrix}{\sigma }\\[-5pt]{\longrightarrow }\end{smallmatrix}}q_{2}}$ 2 ${\textstyle q_{1}{\begin{smallmatrix}{\sigma }\\[-5pt]{\longrightarrow }\end{smallmatrix}}q_{2}}$ (\ $textstyle q_{1}{\time}\[-5pt]{\longrightarrow}\end{smallmatrix}q_{2$

다이어그램 측면에서, 오토마톤은 단어 $=$ $\omega =\omega _{1}\omega _{2}\dots \omega _{m}$ 1 $\omega =\omega _{1}\omega _{2}\dots \omega _{m}$ 2 … $\omega =\omega _{1}\omega _{2}\dots \omega _{m}$ m $\omega =\omega _{1}\omega _{2}\dots \omega _{m}$ { $displaystyle$ \ opha _ {1}\ $opha$ _ { $2}\opha \opha$ _ ${m}$ 을 $\omega =\omega _{1}\omega _{2}\dots \omega _{m}$ (를) 인식한다 $.$ 이는 F의 초기 $q_{0}$ {\ $displaystyle q_{0$ }}에서 $q_{0}$ $q\in F$ 최종 $q\in F$ {\ $displaystyle q_$ {0 $}$ 까지의 경로가 있는 $경우$ 에만 해당된다.path $\omega$ ${\$ \ $displaystyle$ \ $obega$ $\omega$ 자동으로 인식되는 단어 세트는 자동이 인식하도록 설정된 언어를 형성합니다.이 용어에서S(\ $displaystyle$ S $)$ 의 접미사 오토마톤에 의해 인식되는 언어는 접미사 ^[9]언어(공백일 수 있음)입니다.

자동 상태

$L$ 에 대한 $\omega$ ${\$ { \ $displaystyle$ $\omega$ \ obega $L$ }의 $\omega$ $L$ $[\omega ]_{R}=\{\alpha :\omega \alpha \in L\}$ "오른쪽 컨텍스트"는 집합 [ $[\omega ]_{R}=\{\alpha :\omega \alpha \in L\}$ ] $[\omega ]_{R}=\{\alpha :\omega \alpha \in L\}$ $[\omega ]_{R}=\{\alpha :\omega \alpha \in L\}$ $[\omega ]_{R}=\{\alpha :\omega \alpha \in L\}$ α : $[\omega ]_{R}=\{\alpha :\omega \alpha \in L\}$ $[\omega ]_{R}=\{\alpha :\omega \alpha \in L\}$ $[\omega ]_{R}=\{\alpha :\omega \alpha \in L\}$ } { \ $displaystyle$ [ \ $obega$ ] $_$ { R } = \ { \ { \ { \ $alpha :\ oba$ \ $in$ $L$ $}$ 이며 $\alpha$ $,$ 이러한 $\alpha$ 의 $집합$ 이다.는 L{\ $displaystyle$ L $L$ 에서 단어를 형성합니다. 오른쪽 문맥은 모든 단어 집합에서 자연스러운 동등성 $[\alpha ]_{R}=[\beta ]_{R}$ 관계를 $[\alpha ]_{R}=[\beta ]_{R}$ 합니다 $[\alpha ]_{R}=[\beta ]_{R}$ [ $α$ ] R $[\alpha ]_{R}=[\beta ]_{R}$ [ $[\alpha ]_{R}=[\beta ]_{R}$ β ] $[\alpha ]_{R}=[\beta ]_{R}$ { { $displaystyle [$ \ $alpha$ ] $_{R$ } = [ \ $beta$ ] $_{$ R $[\alpha ]_{R}=[\beta ]_{R}$ }L(\ $displaystyle$ L $)$ $L$ 가 $L$ 어떤 결정론적 유한 오토마톤에 의해 인식되는 경우, 동일한 언어를 인식하고 가능한 최소 수의 상태를 갖는 동형 자동자까지 고유한 것이 존재합니다.이러한 자동화를 주어진 $언어$ L $(\displaystyle$ L $L$ 에 대한 최소 자동화라고 합니다. Myhill-Nerode 정리를 통해 올바른 컨텍스트의 ^[11]^[12]관점에서 명시적으로 정의할 수 있습니다.

정리 - 알파벳 $\Sigma$ (\ $displaystyle \Sigma)$ 에 $\Sigma$ 대한 $언어$ L(\ $displaystyle$ L $)$ 을 $L$ 인식하는 최소 자동화는 다음과 같이 명시적으로 정의할 수 있습니다.

$\Sigma$ ${\(\displaystyle \Sigma)$ 는 $\Sigma$ 그대로입니다.
$상태$ Q(\ $displaystyle$ Q $)$ 는 $Q$ 모든 $\omega \in \Sigma ^{*}$ 한 $[\omega ]_{R}$ 단어 $(\$ $\omega \in \Sigma ^{*}$ 에 $[\omega ]_{R}$ 대응합니다 $.\$
초기 $q_{0}$ $q_{0}$ 0 $({$ 은 $q_0$ $[\varepsilon ]_{R}$ 빈 단어 $[\varepsilon ]_{R}$ [ $R$ {\ $displaystyle [\varepsilon ]_{$ R $[\varepsilon ]_{R}$ 의 오른쪽 컨텍스트에 대응합니다.
Final $state$ F { $displaystyle$ F $[\omega ]_{R}$ 는 $\omega \in L$ L $\omega \in L$ l l from from $の$ $[\omega ]_{R}$ from $\$ $displaystyle \$ $]_$ ${$ R $}$ 의 오른쪽 컨텍스트에 $F$ 대응합니다.
$\delta$ ${\$ （ \ $displaystyle$ \ $delta }$ 는 $\delta$ [ $[\omega ]_{R}{\begin{smallmatrix}{\sigma }\\[-5pt]{\longrightarrow }\end{smallmatrix}}[\omega \sigma ]_{R}$ [ ] ] $[\omega ]_{R}{\begin{smallmatrix}{\sigma }\\[-5pt]{\longrightarrow }\end{smallmatrix}}[\omega \sigma ]_{R}$ ] $[\omega ]_{R}{\begin{smallmatrix}{\sigma }\\[-5pt]{\longrightarrow }\end{smallmatrix}}[\omega \sigma ]_{R}$ { \ $displaystyle$ [ \ $메가 ]_{ R$ } { \ $begin$ { $small matrix$ } { \ $sigma$ } \ \ \ \ \ [ $5pt$ } \ long $rightarrow$ } \ } \ {{ [ \ $[\omega ]_{R}{\begin{smallmatrix}{\sigma }\\[-5pt]{\longrightarrow }\end{smallmatrix}}[\omega \sigma ]_{R}$ $\omega \in \Sigma ^{*}$ $[\omega ]_{R}{\begin{smallmatrix}{\sigma }\\[-5pt]{\longrightarrow }\end{smallmatrix}}[\omega \sigma ]_{R}$ } { \ } { \ } { } { $[\omega ]_{R}{\begin{smallmatrix}{\sigma }\\[-5pt]{\longrightarrow }\end{smallmatrix}}[\omega \sigma ]_{R}$ } { } { } { } { } { } { } { } $ma }$ 。

이러한 용어로, "자동화"는 $S=s_{1}s_{2}\dots s_{n}$ S $S=s_{1}s_{2}\dots s_{n}$ $S=s_{1}s_{2}\dots s_{n}$ $S=s_{1}s_{2}\dots s_{n}$ $S=s_{1}s_{2}\dots s_{n}$ … $S=s_{1}s_{2}\dots s_{n}$ s $S=s_{1}s_{2}\dots s_{n}$ { $displaystyle S$ = $s_{1} s_{2$ }\ $dots s_{$ n $S=s_{1}s_{2}\dots s_{n}$ 의 접미어 언어를 인식하는 최소 결정론적 유한 자동화이다.이 언어의 오른쪽 $\omega$ 는 $\omega$ $\omega \alpha$ {\ $displaystyle$ \ $opha$ $}$ 가 S {\ $displaystyle$ S $S$ 의 $\omega \alpha$ 접미사인 $\alpha$ α {\ $displaystyle$ \alpha $}$ 로 $\omega$ 구성되어 있으며, 오른쪽 컨텍스트와 오른쪽 컨텍스트 사이의 분사를 정의하는 다음과 같은 lema를 공식화할 수 있습니다.S $\displaystyle$ S $S$ ^[13]^[14]에서 발생한 올바른 위치 집합:

정리 : $endpos(\omega )=\{r:\omega =s_{l}\dots s_{r}\}$ $endpos(\omega )=\{r:\omega =s_{l}\dots s_{r}\}$ d $endpos(\omega )=\{r:\omega =s_{l}\dots s_{r}\}$ $endpos(\omega )=\{r:\omega =s_{l}\dots s_{r}\}$ s ( $endpos(\omega )=\{r:\omega =s_{l}\dots s_{r}\}$ ) $endpos(\omega )=\{r:\omega =s_{l}\dots s_{r}\}$ { $endpos(\omega )=\{r:\omega =s_{l}\dots s_{r}\}$ : $endpos(\omega )=\{r:\omega =s_{l}\dots s_{r}\}$ $endpos(\omega )=\{r:\omega =s_{l}\dots s_{r}\}$ $endpos(\omega )=\{r:\omega =s_{l}\dots s_{r}\}$ l $endpos(\omega )=\{r:\omega =s_{l}\dots s_{r}\}$ $endpos(\omega )=\{r:\omega =s_{l}\dots s_{r}\}$ $endpos(\omega )=\{r:\omega =s_{l}\dots s_{r}\}$ $}$ { $displaystyle endpos$ ( \ $메가$ ) = \ { $r$ : \ $obega$ = $s$ _ { $l$ } \ $displaystyle$ s $_$ { $r$ $}$ \ $S$ } $be$ $\omega$ $be$ be berences of of ofof of of of $\omega$ theorem of of of of of of of of of of of of ofof of of of of of of of of of of of of of of of of of of of of of of of of of of of of of of

$endpos(\omega )$ $endpos(\omega )$ d $endpos(\omega )$ $endpos(\omega )$ s ( $endpos(\omega )$ " $){$ $displaystyle endpos$ ( \ $endpos(\omega )$ $[\omega ]_{R}$ $[\omega ]_{R}$ 와 $endpos(\omega )$ [ $[\omega ]_{R}$ { $displaystyle$ [ $\$ obega ] $_{R$ $endpos(\omega )$ 에는 다음 분사가 있습니다.

x $x\in endpos(\omega )$ e $x\in endpos(\omega )$ $x\in endpos(\omega )$ $x\in endpos(\omega )$ s ( $x\in endpos(\omega )$ \ $display style$ x \ $in endpos$ ( \ $obega$ ) $x\in endpos(\omega )$ 의 경우 $s_{x+1}s_{x+2}\dots s_{n}\in [\omega ]_{R}$ + $s_{x+1}s_{x+2}\dots s_{n}\in [\omega ]_{R}$ $s_{x+1}s_{x+2}\dots s_{n}\in [\omega ]_{R}$ + $s_{x+1}s_{x+2}\dots s_{n}\in [\omega ]_{R}$ ... $s_{x+1}s_{x+2}\dots s_{n}\in [\omega ]_{R}$ s n ] [ $s_{x+1}s_{x+2}\dots s_{n}\in [\omega ]_{R}$ ${$ $display$ style s $_ { x$ + 1) s $_ {$ $x$ $+$ 2 \ $dots s _$ { $n$ } \ $in$ [ \ $obega$ ]{ $R$ } ;
$[$ $\alpha \in [\omega ]_{R}$ R { $displaystyle$ \alpha $\in$ [ \ $obega ]_{$ R $\alpha \in [\omega ]_{R}$ 인 $n-\vert \alpha \vert \in endpos(\omega )$ - $n-\vert \alpha \vert \in endpos(\omega )$ $n-\vert \alpha \vert \in endpos(\omega )$ $n-\vert \alpha \vert \in endpos(\omega )$ $n-\vert \alpha \vert \in endpos(\omega )$ p $n-\vert \alpha \vert \in endpos(\omega )$ ( $n-\vert \alpha \vert \in endpos(\omega )$ ) \ $displaystyle n$ - \ $vert \ vert$ \ in $endpos$ ( \ $n-\vert \alpha \vert \in endpos(\omega )$ obega ) $n-\vert \alpha \vert \in endpos(\omega )$ } 。

예를 들어, $S=abacaba$ S $S=abacaba$ $S=abacaba$ $S=abacaba$ $S=abacaba$ $S=abacaba$ $S=abacaba$ {\ $displaystyle$ S $=abacaba}$ 와 $S=abacaba$ 그 서브워드 $\omega =ab$ {\ $displaystyle \oba=b$ 의 $endpos(ab)=\{2,6\}$ , $endpos(ab)=\{2,6\}$ $endpos(ab)=\{2,6\}$ s $endpos(ab)=\{2,6\}$ $endpos(ab)=\{2,6\}$ { 2, $endpos(ab)=\{2,6\}$ 6 $endpos(ab)=\{2,6\}$ } { $displaystyle endpos$ (ab) = $\{$ 2, $6$ $[ab]_{R}=\{a,acaba\}$ 및 b $[ab]_{R}=\{a,acaba\}$ } { $[ab]_{R}=\{a,acaba\}$ $[ab]_{R}=\{a,acaba\}$ } r, $[ab]_{R}=\{a,acaba\}$ }, a = a 、 ${R}=\{a,acaba$ 비공식적으로 $[ab]_{R}$ $[ab]_{R}$ ${\$ { $R}$ 은 $[ab]_{R}$ $($ 는) $S$ 의 끝부분까지 b(\ $displaystyle$ ab $)$ 가 $ab$ $이어지는$ 단어로 $endpos(ab)$ 되며, $endpos(ab)$ d $o$ s $)$ 는 이러한 $endpos(ab)$ 발생의 올바른 위치에 의해 형성됩니다 $.$ 이 예에서 $x=2\in endpos(ab)$ x $x=2\in endpos(ab)$ $x=2\in endpos(ab)$ $x=2\in endpos(ab)$ $x=2\in endpos(ab)$ $x=2\in endpos(ab)$ $x=2\in endpos(ab)$ $x=2\in endpos(ab)$ $x=2\in endpos(ab)$ ( $x=2\in endpos(ab)$ ){ $displaystyle$ x = $x=2\in endpos(ab)$ 2 \ $s_{3}s_{4}s_{5}s_{6}s_{7}=acaba\in [ab]_{R}$ endpos $( ab$ ) $s_{3}s_{4}s_{5}s_{6}s_{7}=acaba\in [ab]_{R}$ $s_{3}s_{4}s_{5}s_{6}s_{7}=acaba\in [ab]_{R}$ $s_{3}s_{4}s_{5}s_{6}s_{7}=acaba\in [ab]_{R}$ a $s_{3}s_{4}s_{5}s_{6}s_{7}=acaba\in [ab]_{R}$ [ [ $s_{3}s_{4}s_{5}s_{6}s_{7}=acaba\in [ab]_{R}$ ]R ${$ { $displaystyle s _$ { $s_{3}s_{4}s_{5}s_{6}s_{7}=acaba\in [ab]_{R}$ s _ { 4 } $s _$ { $s_{3}s_{4}s_{5}s_{6}s_{7}=acaba\in [ab]_{R}$ $s_{3}s_{4}s_{5}s_{6}s_{7}=acaba\in [ab]_{R}$ n $pos$ ( $ab$ ) s } s = { $ac$ } $s_{3}s_{4}s_{5}s_{6}s_{7}=acaba\in [ab]_{R}$ with withrespondsrespondsrespondsrespondsrespondsrespondsrespondsrespondsrespondsrespondsrespondsrespondsrespondsresponds with in $s_{3}s_{4}s_{5}s_{6}s_{7}=acaba\in [ab]_{R}$ in in in in in in in ${R}$ 은 $s_{3}s_{4}s_{5}s_{6}s_{7}=acaba\in [ab]_{R}$ (는) 단어 a $a\in [ab]_{R}$ [ $a\in [ab]_{R}$ b ] $a\in [ab]_{R}$ $\$ $displaystyle$ a \ $in [$ ab ] $_$ { $R}}$ 은 $a\in [ab]_{R}$ (는) 요소 $7-|a|=6\in endpos(ab)$ - a $7-|a|=6\in endpos(ab)$ $7-|a|=6\in endpos(ab)$ $7-|a|=6\in endpos(ab)$ d p $7-|a|=6\in endpos(ab)$ s ( $)$ { $display 7-a =6\in$ endpos $(ab$ 에 대응합니다 $.$

[ $[\alpha ]_{R}$ {\ $displaystyle$ [\ $alpha ]_{$ R $[\alpha ]_{R}$ $[\beta ]_{R}$ $[\beta ]_{R}$ [ $]$ R { $displaystyle$ [\ $beta$ $]_{$ R $[\beta ]_{R}$ }}이 적어도1개의 공통 $요소$ x {\ $displaystyle x$ $x$ 를 $endpos(\alpha )$ 가지고 $endpos(\alpha )$ 경우 $endpos(\alpha )$ $endpos(\alpha )$ $(α)$ $endpos(\beta )$ $en$ $($ 도 $endpos(\beta )$ 공통 요소입니다. $,$ α $(\displaystyle$ \alpha $)$ 는 $\alpha$ $\beta$ β $(\$ $displaystyle$ \ $beta$ $)$ 의 $\beta$ $endpos(\beta )\subset endpos(\alpha )$ 이므로 $endpos(\beta )\subset endpos(\alpha )$ $(β$ $[\beta ]_{R}\subset [\alpha ]_{R}$ $n$ $endpos(\beta )\subset endpos(\alpha )$ $endpos(\beta )\subset endpos(\alpha )$ (\ $beta$ )\ $subset$ $[\beta ]_{R}\subset [\alpha ]_{R}$ （\alpha $endpos(\beta )\subset endpos(\alpha )$ ） R $[\beta ]_{R}\subset [\alpha ]_{R}$ [ $[\beta ]_{R}\subset [\alpha ]_{R}$ ] R $[\beta ]_{R}\subset [\alpha ]_{R}$ [ displaystyle [ \ $beta$ ] $_\seta$ ]의 서픽스입니다 $.$ $a\in [ab]_{R}\cap [cab]_{R}$ ${R}\cap [cab]_$ ${R$ $즉$ b{ $displaystyle$ ab}는 $ab$ c $a$ $b$ { $displaystyle$ cab}의 $cab$ 서픽스이므로 $[cab]_{R}=\{a\}\subset \{a,acaba\}=[ab]_{R}$ [ $c$ $[cab]_{R}=\{a\}\subset \{a,acaba\}=[ab]_{R}$ $[cab]_{R}=\{a\}\subset \{a,acaba\}=[ab]_{R}$ $[cab]_{R}=\{a\}\subset \{a,acaba\}=[ab]_{R}$ { $[cab]_{R}=\{a\}\subset \{a,acaba\}=[ab]_{R}$ , $[cab]_{R}=\{a\}\subset \{a,acaba\}=[ab]_{R}$ $[cab]_{R}=\{a\}\subset \{a,acaba\}=[ab]_{R}$ $[cab]_{R}=\{a\}\subset \{a,acaba\}=[ab]_{R}$ } $[cab]_{R}=\{a\}\subset \{a,acaba\}=[ab]_{R}$ [ $[cab]_{R}=\{a\}\subset \{a,acaba\}=[ab]_{R}$ b $[cab]_{R}=\{a\}\subset \{a,acaba\}=[ab]_{R}$ { $[cab]_{R}=\{a\}\subset \{a,acaba\}=[ab]_{R}$ [ cab $]_$ ${R}=\{a\}\subset \{a,acaba\}=[ab]_$ ${R}$ $endpos(cab)=\{6\}\subset \{2,6\}=endpos(ab)$ $endpos(cab)=\{6\}\subset \{2,6\}=endpos(ab)$ n $endpos(cab)=\{6\}\subset \{2,6\}=endpos(ab)$ $endpos(cab)=\{6\}\subset \{2,6\}=endpos(ab)$ $endpos(cab)=\{6\}\subset \{2,6\}=endpos(ab)$ s ( $endpos(cab)=\{6\}\subset \{2,6\}=endpos(ab)$ $endpos(cab)=\{6\}\subset \{2,6\}=endpos(ab)$ ) $endpos(cab)=\{6\}\subset \{2,6\}=endpos(ab)$ { $endpos(cab)=\{6\}\subset \{2,6\}=endpos(ab)$ } $endpos(cab)=\{6\}\subset \{2,6\}=endpos(ab)$ { $endpos(cab)=\{6\}\subset \{2,6\}=endpos(ab)$ , 6 $endpos(cab)=\{6\}\subset \{2,6\}=endpos(ab)$ } $endpos(cab)=\{6\}\subset \{2,6\}=endpos(ab)$ $endpos(cab)=\{6\}\subset \{2,6\}=endpos(ab)$ n $endpos(cab)=\{6\}\subset \{2,6\}=endpos(ab)$ $endpos(cab)=\{6\}\subset \{2,6\}=endpos(ab)$ $endpos(cab)=\{6\}\subset \{2,6\}=endpos(ab)$ s ( $endpos(cab)=\{6\}\subset \{2,6\}=endpos(ab)$ ) $endpos(cab)=\{6\}\subset \{2,6\}=endpos(ab)$ \ $display endpos$ ( $cab$ ) = \ { 6 \ } \ $display$ \ { $2$ , 6 \ } $= endpos ( ab$ ) ;
$[\alpha ]_{R}=[\beta ]_{R}$ $[\alpha ]_{R}=[\beta ]_{R}$ $[\alpha ]_{R}=[\beta ]_{R}$ [ $[\alpha ]_{R}=[\beta ]_{R}$ β $[\alpha ]_{R}=[\beta ]_{R}$ ] $[\alpha ]_{R}=[\beta ]_{R}$ {\ $displaystyle [\alpha$ ]_{R} = [\ $beta ]_$ R}인 $\alpha$ $endpos(\alpha )=endpos(\beta )$ $endpos(\alpha )=endpos(\beta )$ ( $endpos(\alpha )=endpos(\beta )$ ) = $dpos$ ( $β$ $endpos$ (\ $displaystyle$ \ $alpha }$ $S$ 에만 $S$ 표시된다 $.$ $tyle \alpha = b$ $\beta =ab$ β $\beta =ab$ $\beta =ab$ $[b]_{R}=[ab]_{R}=\{a,acaba\}$ { $[b]_{R}=[ab]_{R}=\{a,acaba\}$ $displaystyle$ \ $displaystyle =$ $[b]_{R}=[ab]_{R}=\{a,acaba\}$ $\beta =ab$ } $[b]_{R}=[ab]_{R}=\{a,acaba\}$ { $[b]_{R}=[ab]_{R}=\{a,acaba\}$ , $[b]_{R}=[ab]_{R}=\{a,acaba\}$ $[b]_{R}=[ab]_{R}=\{a,acaba\}$ $[b]_{R}=[ab]_{R}=\{a,acaba\}$ a $[b]_{R}=[ab]_{R}=\{a,acaba\}$ { $displaystyle [ b$ ] $_$ ${R}=[ab]_$ ${R}$ $=$ $\{a,acaba\}$ $endpos(b)=endpos(ab)=\{2,6\}$ e $[b]_{R}=[ab]_{R}=\{a,acaba\}$ $endpos(b)=endpos(ab)=\{2,6\}$ $endpos(b)=endpos(ab)=\{2,6\}$ $endpos(b)=endpos(ab)=\{2,6\}$ s ( $endpos(b)=endpos(ab)=\{2,6\}$ )= $endpos(b)=endpos(ab)=\{2,6\}$ $endpos(b)=endpos(ab)=\{2,6\}$ $endpos(b)=endpos(ab)=\{2,6\}$ $endpos(b)=endpos(ab)=\{2,6\}$ s ( $endpos(b)=endpos(ab)=\{2,6\}$ $endpos(b)=endpos(ab)=\{2,6\}$ { $endpos(b)=endpos(ab)=\{2,6\}$ , 6 $}$ { $display style$ endpos (b $)= endpos (ab$ )= \ { 2 $,6$ ;
[ $[\alpha ]_{R}=[\beta ]_{R}$ $[\alpha ]_{R}=[\beta ]_{R}$ $[\alpha ]_{R}=[\beta ]_{R}$ [ $[\alpha ]_{R}=[\beta ]_{R}$ $[\alpha ]_{R}=[\beta ]_{R}$ ${\$ $|\alpha |\leq |\gamma |\leq |\beta |$ ] $_{R$ } $[\alpha ]_{R}=[\gamma ]_{R}=[\beta ]_{R}$ [\ $beta ]_{R}$ 및 β $[\alpha ]_{R}=[\beta ]_{R}$ $\gamma$ ${\$ $displaystyle \leq$ $|\alpha |\leq |\gamma |\leq |\beta |$ 의 $\beta$ 인 경우 $[\alpha ]_{R}=[\beta ]_{R}$ $\beta$ $\gamma$ $|\alpha |\leq |\gamma |\leq |\beta |$ {\ $displaystyle \leq$ \ $leq$ \leq $|\alpha |\leq |\gamma |\leq |\beta |$ 는 $\beta$ [ $[\alpha ]_{R}=[\gamma ]_{R}=[\beta ]_{R}$ R $[\alpha ]_{R}=[\gamma ]_{R}=[\beta ]_{R}$ 의 [ ]이다. $= [\displays$ ]_{ $R}=[\beta$ $[\alpha ]_{R}=[\gamma ]_{R}=[\beta ]_{R}$ _{R}. $[c]_{R}=[bac]_{R}=\{aba\}$ 의 $[c]_{R}=[bac]_{R}=\{aba\}$ 에서는 $[c]_{R}=[bac]_{R}=\{aba\}$ [ $[c]_{R}=[bac]_{R}=\{aba\}$ ] $[c]_{R}=[bac]_{R}=\{aba\}$ [ $[c]_{R}=[bac]_{R}=\{aba\}$ a $[c]_{R}=[bac]_{R}=\{aba\}$ ] $[c]_{R}=[bac]_{R}=\{aba\}$ $[c]_{R}=[bac]_{R}=\{aba\}$ { a b a $}$ { $displaystyle [c$ ] $_$ ${R}=[bac]_$ { $R}=\{aba\}:$ [ $[ac]_{R}=\{aba\}$ $[ac]_{R}=\{aba\}$ $[ac]_{R}=\{aba\}$ { $[ac]_{R}=\{aba\}$ $[ac]_{R}=\{aba\}$ a $}$ { $displaystyle$ [ $ac]_인$ $[ac]_{R}=\{aba\}$ 접미사" $=$ $\gamma =ac$ ${\displaystyle$ \ $displaystyle$ $=$ $ac}$ 에 $[c]_{R}=[bac]_{R}=\{aba\}$ $\gamma =ac$ 해당합니다 $.$ ${R}=\{aba$

접미사 오토마톤의 모든 $q=[\alpha ]_{R}$ q $=$ [ $α$ ] $q=[\alpha ]_{R}$ {\ $displaystyle$ q $=[\alpha ]_{$ R $q=[\alpha ]_{R}$ }}은 이 ^[14]상태에서 인식되는 가장 긴 단어의 중첩된 접미사를 연속적으로 인식한다.

"왼쪽 확장" $←$ $\gamma$ 의 ${{$ $displaystyle\displaystyle\$ displaystyle} ${\displaystyle$ $}$ 은 $\gamma$ (는) ${\$ {\displaystyle $\displaystyle$ $}$ 과 ${\overset {\scriptstyle {\leftarrow }}{\gamma }}$ $\omega$ (와) 오른쪽 컨텍스트가 같은 가장 긴 $문자열입니다.$ $|{\overset {\scriptstyle {\leftarrow }}{\gamma }}|$ $|{\overset {\scriptstyle {\leftarrow }}{\gamma }}|$ $style\$ displaystyle {style $}$ \ $leftarrow$ }}}{\display $}}$ 은 $|{\overset {\scriptstyle {\leftarrow }}{\gamma }}|$ $($ 는 $len(q)$ $q=[\gamma ]_{R}$ $len(q)$ [ $]$ $len(q)$ {\ $displaystyle$ q $q=[\gamma ]_{R}$ = $[\$ $display$ $]_{$ R $q=[\gamma ]_{R}$ } 로 인식되는 가장 긴 문자열의 {\ $displaystyle$ len $(q$ 로 표시됩니다.다음과 ^[15]같이 표시됩니다.

$\gamma$ — $§$ { $displaystyle$ $\displaystyle$ ${\overleftarrow {\gamma }}=\beta \gamma$ }의 왼쪽 ${\overleftarrow {\gamma }}=\beta \gamma$ 는 β $=$ β ${\overleftarrow {\gamma }}=\beta \gamma$ { $displaystyle$ $\beta$ \ $displaystyle$ \ $display$ $\gamma$ $}$ = \ $displaystyle$ \ $display$ ${\overleftarrow {\gamma }}=\beta \gamma$ $}$ ${\$ $}$ {\ {\ $\beta$ theorem theorem theorem theorem theorem theorem theorem theorem ← theorem theorem theorem theorem theorem theorem theorem theorem theorem theorem theorem theorem theorem theorem theorem theorem theorem theorem theorem theorem theorem theorem theorem theorem theorem $\beta$ $yle \syslogs$ $\beta$ 。

$q=[\alpha ]_{R}$ q $q=[\alpha ]_{R}$ [ $q=[\alpha ]_{R}$ α ] $q=[\alpha ]_{R}$ {\ $displaystyle$ q = [\ $alpha ]_{R}$ 의 $q=[\alpha ]_{R}$ "Suffix link" $link(q)$ $link(q)$ $link(q)$ ( $link(q)$ q $)$ { $displaystyle$ $q$ $q$ }는 $link(q)$ $\alpha$ q { $displaystyle$ $}$ 에서 인식되지 않는 α의 $\alpha$ 접미사를 포함하는 $상태$ p { $displaystyle$ $p$ $}$ 에 $p$ 대한 포인터입니다.

q $q=[\alpha ]_{R}$ [ $q=[\alpha ]_{R}$ α ] $q=[\alpha ]_{R}$ { $displaystyle$ q ${\overset {\scriptstyle {\leftarrow }}{\alpha }}$ [ \ $alpha$ ] $_$ { $R }$ $}$ $display$ { $displaystyle$ { $script style$ } { \ $alpha }$ ${\overset {\scriptstyle {\leftarrow }}{\alpha }}$ 、 l $len(link(q))$ $len(link(q))$ k $len(link(q))$ （ $len(link(q))$ $len(q)$ $）$ $len(q)$ 또,^[15] 다음과 같은 것이 있습니다.

정리 - 접미사 링크는 ${\mathcal {T}}(V,E)$ T ${\mathcal {T}}(V,E)$ $)$ 를 형성합니다.{ $displaystyle$ \ $mathcal$ { ${\mathcal {T}}(V,E)$ T $}$ （ $V$ 、 $E$ ）。이러한 ${\mathcal {T}}(V,E)$ 링크는 다음과 같이 명시적으로 정의할 수 있습니다.

트리의 $꼭지점$ V(\ $displaystyle$ V $)$ 는 $V$ 모든 $(\displaystyle$ S $)$ 서브스트링의 $S$ 왼쪽 ${\overleftarrow {\omega }}$ $←$ {\ $displaystyle {\overleftarrow}$ 에 $해당합니다$
트리의 $모서리$ E $(\$ $displaystyle$ $E)$ 는 $E$ $({\overleftarrow {\omega }},{\overleftarrow {\alpha \omega }})$ ${\overleftarrow {\omega }}\neq {\overleftarrow {\alpha \omega }}$ $display$ ${\overleftarrow {\omega }}\neq {\overleftarrow {\alpha \omega }}$ $\alpha \in \Sigma$ $({\overleftarrow {\omega }},{\overleftarrow {\alpha \omega }})$ $({\overleftarrow {\omega }},{\overleftarrow {\alpha \omega }})$ $({\overleftarrow {\omega }},{\overleftarrow {\alpha \omega }})$ α display $over 、$ $α$ display $({\overleftarrow {\omega }},{\overleftarrow {\alpha \omega }})$ $、$ $({\overleftarrow {\omega }},{\overleftarrow {\alpha \omega }})$ ${\overleftarrow {\omega }}\neq {\overleftarrow {\alpha \omega }}$ over display display display display display display display $display$ display display display ${\overleftarrow {\omega }}\neq {\overleftarrow {\alpha \omega }}$ $display$ display display display display display display overdisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplayoverdisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplayoverdisplaydisplaydisplaydisplaydisplayoverdisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplayoverdisplaydisplayoverdisplaydisplaydisplaydisplaydisplaydisplayoveroverdisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplayover $ega }}}$ 입니다 ${\overleftarrow {\omega }}\neq {\overleftarrow {\alpha \omega }}$

접미사 트리를 사용한 연결

접미사 트리, 접미사 트리, DAWG 및 CDAWG의 관계

"프리픽스 트리"(또는 "트리")는 동일한 문자로 표시된 두 개의 나가는 호를 가진 $정점$ v $\style$ v}가 $v$ 없는 방식으로 호가 문자로 표시된 루트 방향 트리입니다.trie의 일부 정점은 최종으로 표시됩니다.Trie는 어근에서 최종 꼭지점까지의 경로에 의해 정의된 단어 집합을 인식한다고 한다.이와 같이 프리픽스 트리는 루트를 초기 ^[16]정점으로 인식할 경우 특별한 종류의 결정론적 유한 오토마타입니다. $(\$ displaystyle S)라는 $S$ 단어의 "suffix trie"는 일련의 접미사를 인식하는 접두사 트리입니다."접미사 트리"는 압축절차를 통해 접미사 트리로부터 얻은 트리이며, 그 사이에 정점의 정도가 ^[15]2일 경우 후속 에지가 병합된다.

그 정의에 따르면 서픽스 트리e를 최소화함으로써 서픽스 오토마톤을 얻을 수 있다.접미사 트리의 최소화와(접미사 ^[17]트리의 가장자리에 있는 각 문자열이 알파벳의 솔리드 문자라고 가정할 경우) 접미사 오토마톤의 콤팩트화를 통해 압축된 접미사 오토마톤을 얻을 수 있음을 알 수 있다.접미사 트리와 같은 문자열의 접미사 오토마톤 간에는 이러한 연결 이외에도 $S=s_{1}s_{2}\dots s_{n}$ S $S=s_{1}s_{2}\dots s_{n}$ $S=s_{1}s_{2}\dots s_{n}$ $S=s_{1}s_{2}\dots s_{n}$ $S=s_{1}s_{2}\dots s_{n}$ 2 … $S=s_{1}s_{2}\dots s_{n}$ n \ $displaystyle$ S $= s_{2}\dots s_{n}$ 의 $S=s_{1}s_{2}\dots s_{n}$ 접미사 오토마톤과 반전 $S^{R}=s_{n}s_{n-1}\dots s_{1}$ S $S^{R}=s_{n}s_{n-1}\dots s_{1}$ $S^{R}=s_{n}s_{n-1}\dots s_{1}$ $S^{R}=s_{n}s_{n-1}\dots s_{1}$ $S^{R}=s_{n}s_{n-1}\dots s_{1}$ - $S^{R}=s_{n}s_{n-1}\dots s_{1}$ 1 $S^{R}=s_{n}s_{n-1}\dots s_{1}$ S $S^{R}=s_{n}s_{n-1}\dots s_{1}$ ^ 1 $사이$ 의 연결도 있습니다. ${R}=s_{n}s_{n-1}\dots s_{1$ ^[18]

오른쪽 컨텍스트와 마찬가지로 "왼쪽 $[\omega ]_{L}=\{\beta \in \Sigma ^{*}:\beta \omega \in L\}$ " $[\omega ]_{L}=\{\beta \in \Sigma ^{*}:\beta \omega \in L\}$ [ ] L $[\omega ]_{L}=\{\beta \in \Sigma ^{*}:\beta \omega \in L\}$ { $[\omega ]_{L}=\{\beta \in \Sigma ^{*}:\beta \omega \in L\}$ $[\omega ]_{L}=\{\beta \in \Sigma ^{*}:\beta \omega \in L\}$ $[\omega ]_{L}=\{\beta \in \Sigma ^{*}:\beta \omega \in L\}$ $[\omega ]_{L}=\{\beta \in \Sigma ^{*}:\beta \omega \in L\}$ L $[\omega ]_{L}=\{\beta \in \Sigma ^{*}:\beta \omega \in L\}$ \ $displaystyle$ [ \ $omega ]_{$ L } $=$ \ { \ $beta$ \ in \ Sigma ^ { * $[\omega ]_{L}=\{\beta \in \Sigma ^{*}:\beta \omega \in L\}$ } : \ $extensions$ \ $in$ L $[\omega ]_{L}=\{\beta \in \Sigma ^{*}:\beta \omega \in L\}$ \ sigma $→$ \ set style 、 $"오른쪽 확장$ $[\omega ]_{L}=\{\beta \in \Sigma ^{*}:\beta \omega \in L\}$ (\ $script$ ) $ωsetsetsetsetsetsetsetsetstylesetsetsetsetstylestyleensionsensions$ {\ {\ ${\overset {\scriptstyle {\rightarrow }}{\omega ~}}$ {\styleensions {\ {\ {\ {\ωωω\ {\ωstylestylestylestyle → $s$ { $displaystyle$ \ $omega$ } 및 $\omega$ 등가 $[\alpha ]_{L}=[\beta ]_{L}$ 관계 [ $[\alpha ]_{L}=[\beta ]_{L}$ ] $[\alpha ]_{L}=[\beta ]_{L}$ $=$ [ $[\alpha ]_{L}=[\beta ]_{L}$ β ] $[\alpha ]_{L}=[\beta ]_{L}$ { $displaystyle [\alpha ]_{L$ 문자열 $S$ 의 " $language$ " L ${\$ $displaystyle$ L $}$ 과 $L$ $S$ 관련하여 올바른 확장자를 고려하는 경우 다음을 얻을 ^[15]수 있습니다.

정리 - $문자열$ S $(\displaystyle$ S $)$ 의 $S$ 접미사 트리는 다음과 같이 명시적으로 정의할 수 있습니다.

트리의 $꼭지점$ V(\ $displaystyle$ V $)$ 는 $V$ $모든$ S $(\displaystyle$ S $)$ 서브스트링의 $S$ ${\overrightarrow {\omega }}$ 확장 $→(\$ 에 ${\overrightarrow {\omega }}$ 해당합니다.
$엣지$ E(\ $displaystyle$ $E)$ 는 $E$ x $display$ ${\overrightarrow {\omega x}}={\overrightarrow {\omega }}x\alpha$ $({\overrightarrow {\omega }},x\alpha ,{\overrightarrow {\omega x}})$ ${\overrightarrow {\omega x}}={\overrightarrow {\omega }}x\alpha$ $display display$ ${\overrightarrow {\omega x}}={\overrightarrow {\omega }}x\alpha$ $x\in \Sigma$ 、 x → display display display ${\overrightarrow {\omega x}}={\overrightarrow {\omega }}x\alpha$ display display display display displaydisplay → $display$ display display display display ${\overrightarrow {\omega x}}={\overrightarrow {\omega }}x\alpha$ display display display $display$ display display display display display display ${\overrightarrow {\omega x}}={\overrightarrow {\omega }}x\alpha$ display display display display display display displaydisplaydisplay display $({\overrightarrow {\omega }},x\alpha ,{\overrightarrow {\omega x}})$ display display display display display display display display display display display display display display display display display $display$ display display display ${\overrightarrow {\omega x}}={\overrightarrow {\omega }}x\alpha$ 를 클릭합니다.

여기서 triplet $(v_{1},\omega ,v_{2})\in E$ ( $(v_{1},\omega ,v_{2})\in E$ 1, $(v_{1},\omega ,v_{2})\in E$ , $(v_{1},\omega ,v_{2})\in E$ ) $(v_{1},\omega ,v_{2})\in E$ e $(v_{1},\omega ,v_{2})\in E$ { \ $displaystyle$ ( $v$ _ { $1$ , \ $(v_{1},\omega ,v_{2})\in E$ $메가$ , v $_$ { $2$ } \ $in$ E $(v_{1},\omega ,v_{2})\in E$ }는 $(v_{1},\omega ,v_{2})\in E$ $v_{1}$ "{ $displaystyle$ \ $}"$ 이 $\omega$ 표시된 $\omega$ $v_{1}$ 1 ~ $v_{2}$ 2 { $displaystyle v _$ $v_{1}$ { $v_{2}$ }의 $v_{1}$ $v_{2}$ 엣지가 있음을 의미합니다.

즉, $S$ 의 $S$ $서픽스$ 링크트리와 $S^{R}$ S $R$ 의 $S^{R}$ 서픽스 $트리$ 는 ^[18]동형입니다.

단어 "abbcbc" 및 "cbcbba"의 접미사 구조
단어 "abbcbc"의 접미사 자동화 단어 "abbcbc"의 접미사 trie, 접미사 트리 및 CDAWG "cbcbba" 단어의 접미사 트리 ('abbcbc' 단어의 Suffix 링크 트리)

왼쪽 확장의 경우와 마찬가지로 오른쪽 ^[15]확장의 경우 다음 보조항목이 유지됩니다.

정리 - $문자열$ 의 $\gamma$ 오른쪽 ${\overrightarrow {\gamma }}=\gamma \alpha$ ${\$ ${\overrightarrow {\gamma }}=\gamma \alpha$ α displaystyle $=$ α displaystyle { } $=$ \ $displaystyle$ \ alpha $}$ 로 ${\overrightarrow {\gamma }}=\gamma \alpha$ ${\overrightarrow {\gamma }}=\gamma \alpha$ 있습니다. $\alpha$ 서 $\alpha$ $\gamma$ 는 $\gamma$ S{ $displaystyle$ \ $alpha$ $\alpha$ $}$ 의 $\alpha$ $\gamma$ $S$ 모든 발생이 성공할 수 있는 가장 긴 단어입니다. $(\displaystyle\displaystyle$

크기

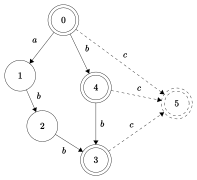
$n>1$ n $n>1$ 의 $문자열$ $n>1$ S(\ $displaystyle$ S $)$ 의 $S$ 서픽스 오토마톤에는 $(\displaystyle 2n-1)$ 상태 $2n-1$ 및 $(\displaystyle 3n-4)$ 의 $3n-4$ 전환이 있습니다.이러한 경계는 $abb\dots bb=ab^{n-1}$ $abb\dots bb=ab^{n-1}$ $abb\dots bb=ab^{n-1}$ … $abb\dots bb=ab^{n-1}$ $abb\dots bb=ab^{n-1}$ $abb\dots bb=ab^{n-1}$ b n $abb\dots bb=ab^{n-1}$ - $abb\dots bb=ab^{n-1}$ ${\$ bb $=$ $ab$ $^{n-1}}$ 및 $abb\dots bb=ab^{n-1}$ $abb\dots bc=ab^{n-2}c$ b … $abb\dots bc=ab^{n-2}c$ $abb\dots bc=ab^{n-2}c$ $abb\dots bc=ab^{n-2}c$ $abb\dots bc=ab^{n-2}c$ - $abb\dots bc=ab^{n-2}c$ { $displaystyle abb\display$ bc $=$ ab^{ $n-2}c}$ c}에 ^[13]대응하여 $abb\dots bc=ab^{n-2}c$ 도달합니다.이것은 $|\delta |\leq |Q|+n-2$ Q + $|\delta |\leq |Q|+n-2$ - 2 $|\delta |\leq |Q|+n-2$ ( \ $displaystyle$ \ $delta$ \ $leq$ + $n-2$ )로 $|\delta |\leq |Q|+n-2$ 보다 엄밀하게 공식화할 수 있습니다. $|\delta |$ 서 {\ $|\delta |$ { $displaystyle$ \ $delta$ }와 $|\delta |$ $|Q|$ （ \ $displaystyle$ Q $|Q|$ ）는 $|Q|$ 대응하는 ^[14]자동화의 트랜지션 및 상태 수입니다.

최대 접미사 오토마타
$ab^{n-1}$ $ab^{n-1}$ - $ab^{n-1}$ 의 접미사 오토마톤({ $display style$ ab $^{n-1})$ $ab^{n-2}c$ n $ab^{n-2}c$ - $ab^{n-2}c$ 의 접미사 오토마톤(\ $displaystyle$ ab^{ $n-2}c)$

건설

처음에 자동화는 빈 단어에 대응하는 단일 상태로만 구성되며, 그 후 문자열의 문자가 하나씩 추가되고 각 단계에서 자동화가 단계적으로 ^[19]재구축된다.

상태 갱신

문자열에 새 문자가 추가된 후 일부 동등성 클래스가 변경됩니다.[ $[\alpha ]_{R_{\omega }}$ $[\alpha ]_{R_{\omega }}$ ${\$ { $display$ style [ \ $alpha ] _$ { $R$ _ { \ $메가$ } $[\alpha ]_{R_{\omega }}$ } $\omega$ ${\$ { $display$ $\alpha$ style \ $omega$ $\alpha$ $}$ 서픽스의 $\omega$ 언어에 관한 $α$ 의 $\alpha$ $\alpha$ 컨텍스트라고 합니다 $[\alpha ]_{R_{\omega }}$ $[\alpha ]_{R_{\omega }}$ 다음 x{\ $displaystyle$ x $x$ $\omega$ $}$ $x$ 에 $[\alpha ]_{R_{\omega }}$ [ $] R$ { $R_{\obega$ $[\alpha ]_{R_{\omega x}}$ 에서 $[\alpha ]_{R_{\omega }}$ $[\alpha ]_{R_{\omega }}$ $[\alpha ]_{R_{\omega x}}$ $[\alpha ]_{R_{\omega x}}$ $[\alpha ]_{R_{\omega x}}$ { $displaystyle [\alpha ]_{$ $R_$ ${\obega$ $\omega$ x $}}$ 로의 천이를 $[\alpha ]_{R_{\omega x}}$ $\omega$ ^[14] $렘마$ 로 정의합니다.

$\alpha ,\omega \in \Sigma ^{*}$ : $\Sigma$ $\alpha ,\omega \in \Sigma ^{*}$ , $\alpha ,\omega \in \Sigma ^{*}$ （ \ $display$ style \ alpha , \ $obega$ \ $in$ \ Sigma $\Sigma$ $^$ { * } some $\alpha ,\omega \in \Sigma ^{*}$ $\Sigma$ $x\in \Sigma$ 、 $x\in \Sigma$ over over $over$ over over over over over over over over over over over displaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplay \ $displaystyle$ $\ Sigma$ \ Sigma \ sigma $。$ 다음으로 [ $[\alpha ]_{R_{\omega }}$ $[\alpha ]_{R_{\omega }}$ ${\$ { \ $displaystyle$ [ \ $alpha ]_$ { R _ { \ obega $[\alpha ]_{R_{\omega }}$ }}과 $[\alpha ]_{R_{\omega }}$ $[\alpha ]_{R_{\omega x}}$ [ $[\alpha ]_{R_{\omega x}}$ $[\alpha ]_{R_{\omega x}}$ $[\alpha ]_{R_{\omega x}}$ x $[\alpha ]_{R_{\omega x}}$ { \ $displaystyle$ [ $[\alpha ]_{R_{\omega x}}$ \ $alpha ]_$ { R $_$ { \ $obega$ x $[\alpha ]_{R_{\omega x}}$ $[\alpha ]_{R_{\omega }}$ 에 다음과 같은 대응이 있습니다.

$[\alpha ]_{R_{\omega x}}=[\alpha ]_{R_{\omega }}x\cup \{\varepsilon \}$ $[\alpha ]_{R_{\omega x}}=[\alpha ]_{R_{\omega }}x\cup \{\varepsilon \}$ $[\alpha ]_{R_{\omega x}}=[\alpha ]_{R_{\omega }}x\cup \{\varepsilon \}$ x $=$ [ $[\alpha ]_{R_{\omega x}}=[\alpha ]_{R_{\omega }}x\cup \{\varepsilon \}$ ] R $[\alpha ]_{R_{\omega x}}=[\alpha ]_{R_{\omega }}x\cup \{\varepsilon \}$ x $[\alpha ]_{R_{\omega x}}=[\alpha ]_{R_{\omega }}x\cup \{\varepsilon \}$ [ { } $}$ { $displaystyle [$ \ $alpha ]_{R_{\ 메가 }}x\$ cup \ { \ $varepsilon \ }$ $\alpha$ α가 $\alpha$ $α$ x { $\ display style \$ $\omega x$ 의 $[\alpha ]_{R_{\omega x}}=[\alpha ]_{R_{\omega }}x\cup \{\varepsilon \}$ 접미사인 $\alpha$
$[\alpha ]_{R_{\omega x}}=[\alpha ]_{R_{\omega }}x$ [ $[\alpha ]_{R_{\omega x}}=[\alpha ]_{R_{\omega }}x$ $[\alpha ]_{R_{\omega x}}=[\alpha ]_{R_{\omega }}x$ $[\alpha ]_{R_{\omega x}}=[\alpha ]_{R_{\omega }}x$ x $=$ [ $[\alpha ]_{R_{\omega x}}=[\alpha ]_{R_{\omega }}x$ ] $[\alpha ]_{R_{\omega x}}=[\alpha ]_{R_{\omega }}x$ $[\alpha ]_{R_{\omega x}}=[\alpha ]_{R_{\omega }}x$ x [ \ $displaystyle [$ \ $alpha ]$ _ ${R_{$ \ $메가$ x }=[ \ $alpha ]_{R_$ { \ obega $}x}$ 이외의 $[\alpha ]_{R_{\omega x}}=[\alpha ]_{R_{\omega }}x$ 경우 $[\alpha ]_{R_{\omega x}}=[\alpha ]_{R_{\omega }}x$

현재 $\omega$ ${\$ 에 x $(\$ $displaystyle$ $x)$ 를 $x$ $\omega$ $x$ 한 후 $\alpha$ α $(\displaystyle$ \ $alpha)$ 의 $\alpha$ $\alpha$ 컨텍스트는 $\alpha$ $\omega x$ (\ $displaystyle \alpha)$ 가 $\alpha$ x $(\displaystyle \obe$ x $\omega x$ 의 접미사인 $\alpha$ 에만 크게 변경됩니다.즉, 등가관계 $\equiv _{R_{\omega x}}$ R $\equiv _{R_{\omega x}}$ x {\displaystyle \ $equiv$ _ ${$ $R_{\omega$ x $}}$ 는 $\equiv _{R_{\omega x}}$ $r$ R $\equiv _{R_{\omega }}$ { $displaystyle$ \ $equiv$ _ ${R_{\$ omega $\equiv _{R_{\omega }}$ 을 개량한 것입니다.즉 $[\alpha ]_{R_{\omega x}}=[\beta ]_{R_{\omega x}}$ [ $[\alpha ]_{R_{\omega x}}=[\beta ]_{R_{\omega x}}$ ] R $[\alpha ]_{R_{\omega x}}=[\beta ]_{R_{\omega x}}$ [ ] R $[\alpha ]_{R_{\omega x}}=[\beta ]_{R_{\omega x}}$ [ $[\alpha ]_{R_{\omega x}}=[\beta ]_{R_{\omega x}}$ ] R $[\alpha ]_{R_{\omega x}}=[\beta ]_{R_{\omega x}}$ \ $display style$ [ \ $alpha$ ] X ] { \ } { \ } { \ } { } { } { } { } { } { } { } { } { } { ${\$ $\equiv _{R_{\omega }}$ { $displaystyle$ [ \ $alpha$ ] $_$ { R _ { \ obega } = [ \ $response ]_$ { R $_$ { \ obega $[\alpha ]_{R_{\omega }}=[\beta ]_{R_{\omega }}$ } $\equiv _{R_{\omega }}$ }. $\equiv _{R_{\omega }}$ r $\equiv _{R_{\omega }}$ ${\$ 2개의 동등 클래스(\ $displaystyle$ \ $equiv _$ { $R$ _ { \ obe $}$ } })가 $\equiv _{R_{\omega }}$ 추가되면 각각 최대 2개의 새로운 클래스로 분할됩니다.첫째, 빈 오른쪽 콘텍스트에 대응하는 동등성 클래스는 항상 2개의 동등성 클래스로 분할됩니다.그 중 하나는 $\omega x$ x ( \ $displaystyle$ \ $메가$ x )자체에 대응하고 { $\{\varepsilon \}$ $}$ ( \ $displaystyle$ \ { \ \ $varepsilon$ \ } )를 $\{\varepsilon \}$ 오른쪽 콘텍스트로 $\{\varepsilon \}$ 합니다.이 새로운 등가 클래스에는 정확하게 $(\$ $displaystyle \obega$ x $)$ 와 $\omega x$ $\omega$ 에서 발생하지 않은 모든 서픽스가 포함됩니다.이러한 단어의 오른쪽 컨텍스트는 이전에는 비어 있었고 현재는 ^[14]빈 단어만 포함되어 있기 때문입니다.

서픽스 오토마톤 상태와 서픽스 트리의 정점과의 대응관계를 고려할 때, 새로운 문자가 부가된 후에 분할될 가능성이 있는 제2의 상태를 찾아낼 수 있다. $「\displaystyle\obe$ $」$ 에서 $\omega$ 「 $(\displaystyle\obe$ x)」로의 이행은, 역스트링의 「 $(\$ $displaystyle\obe ^{R$ })」에서 「 $\omega$ $($ 로의 $x\omega ^{R}$ 이행에 대응합니다 $\omega x$ .서픽스 트리에 관해서는 $\omega ^{R}$ 최장 $x\omega ^{R}$ R ( \ $displaystyle$ x \ $obega ^$ { R $x\omega ^{R}$ )를 $x\omega ^{R}$ $\omega ^{R}$ R ( \ $displaystyle$ \ $obega$ ^ { $R$ } )의 서픽스트리에 삽입하는 것에 대응합니다.이 삽입 후 최대 2개의 새로운 정점이 형성될 수 있습니다.x $x\omega ^{R}$ R ( x $r$ R \ $displaystyle$ x \ ^ ^ $}$ 에 $x\omega ^{R}$ 합니다.나뭇가지가 있었다면 직계 조상에 해당하죠서픽스 오토마타로 돌아가면 첫 번째 새로운 상태가 $\omega x$ θ $\omega x$ 를 $인식$ 하고 $\omega x$ 두 번째 상태(두 번째 새로운 상태가 있는 경우 $)$ 가 서픽스 링크임을 의미합니다.이는 다음과 같은 조건이라고 할 수 있다.^[14]

정리 - $\omega x$ $\omega \in \Sigma ^{*}$ display display display $、$ \ $displaystyle \ in$ \ Sigma $^$ { * $\omega \in \Sigma ^{*}$ } , x $x\in \Sigma$ $\Sigma$ $display$ \ $displaystyle$ $\Sigma$ x\ $in$ \ Sigma $x\in \Sigma$ $\Sigma$ $x\in \Sigma$ , $\omega x$ ${$ \ $displaystyle$ \ sigma $\alpha$ $\omega x$ 는 $\alpha$ x $\style$ 중 가장 긴 $\alpha$ 입니다. $\beta ={\overset {\scriptstyle {\leftarrow }}{\alpha }}$ $\beta ={\overset {\scriptstyle {\leftarrow }}{\alpha }}$ α $←$ {\ $displaystyle$ \ $displaystyle = scriptstyle$ {\ $left 화살표$ }}{\alpha $\beta ={\overset {\scriptstyle {\leftarrow }}{\alpha }}$ $\omega$ 그 후 모든 $서브스트링$ $\omega$ $,$ v ${\$ $displaystyle$ $u$ $,v$ $}$ 는 $u,v$ 다음과 $\omega$ 같이 $\beta ={\overset {\scriptstyle {\leftarrow }}{\alpha }}$ 됩니다.

$[u]_{R_{\omega }}=[v]_{R_{\omega }}$ ] R $[u]_{R_{\omega }}=[v]_{R_{\omega }}$ [ $[u]_{R_{\omega }}=[v]_{R_{\omega }}$ ] $[u]_{R_{\omega }}=[v]_{R_{\omega }}$ { $displaystyle [ u$ ]_인 경우 ${R_{\obega}}=[v]_{R_{\obega}}}$ $[u]_{R_{\omega }}\neq [\alpha ]_{R_{\omega }}$ 및 $[u]_{R_{\omega }}=[v]_{R_{\omega }}$ [ $[u]_{R_{\omega }}\neq [\alpha ]_{R_{\omega }}$ [ $α$ ] $[u]_{R_{\omega }}\neq [\alpha ]_{R_{\omega }}$ { $displaystyle [ u$ ]_ ${R_{\ega }}\neq$ [\ $alpha]_{R_{\ega$ $[u]_{R_{\omega }}\neq [\alpha ]_{R_{\omega }}$ $[u]_{R_{\omega x}}=[v]_{R_{\omega x}}$ [ $[u]_{R_{\omega x}}=[v]_{R_{\omega x}}$ $[u]_{R_{\omega x}}=[v]_{R_{\omega x}}$ $[u]_{R_{\omega x}}=[v]_{R_{\omega x}}$ x $[u]_{R_{\omega x}}=[v]_{R_{\omega x}}$ [ $[u]_{R_{\omega x}}=[v]_{R_{\omega x}}$ ] $[u]_{R_{\omega x}}=[v]_{R_{\omega x}}$ $[u]_{R_{\omega x}}=[v]_{R_{\omega x}}$ x $[u]_{R_{\omega x}}=[v]_{R_{\omega x}}$ { \ $displaystyle [ u$ ] $_$ ${R_{\omega$ x $}}=[v]_{R_{\omega$ x $[u]_{R_{\omega x}}=[v]_{R_{\omega x}}$
$[u]_{R_{\omega }}=[\alpha ]_{R_{\omega }}$ ] R $[u]_{R_{\omega }}=[\alpha ]_{R_{\omega }}$ [ $[u]_{R_{\omega }}=[\alpha ]_{R_{\omega }}$ ] $[u]_{R_{\omega }}=[\alpha ]_{R_{\omega }}$ { $displaystyle [ u$ ]_인 경우 $[u]_{R_{\omega x}}=[\alpha ]_{R_{\omega x}}$ $R_{\obega$ }} $=[\alpha]_$ { $R_$ ${\obega$ }} $\vert u\vert \leq \vert \alpha \vert$ u $α$ {\ {\ 、 [ $[u]_{R_{\omega x}}=[\alpha ]_{R_{\omega x}}$ $\vert u\vert \leq \vert \alpha \vert$ ] R $[u]_{R_{\omega x}}=[\alpha ]_{R_{\omega x}}$ x $[u]_{R_{\omega x}}=[\alpha ]_{R_{\omega x}}$ [ $[u]_{R_{\omega x}}=[\alpha ]_{R_{\omega x}}$ $[u]_{R_{\omega x}}=[\alpha ]_{R_{\omega x}}$ $[u]_{R_{\omega x}}=[\alpha ]_{R_{\omega x}}$ x \ $[u]_{R_{\omega x}}=[\alpha ]_{R_{\omega x}}$ [ $[u]_{R_{\omega x}}=[\alpha ]_{R_{\omega x}}$ $u$ $] _$ $vert$ \ $\vert u\vert \leq \vert \alpha \vert$ ${R_{\obega$ x $}=[\alpha]_{R_{\obega$ x $[u]_{R_{\omega x}}=[\alpha ]_{R_{\omega x}}$
$[u]_{R_{\omega }}=[\alpha ]_{R_{\omega }}$ ] R $[u]_{R_{\omega }}=[\alpha ]_{R_{\omega }}$ [ $[u]_{R_{\omega }}=[\alpha ]_{R_{\omega }}$ ] $[u]_{R_{\omega }}=[\alpha ]_{R_{\omega }}$ { $displaystyle [ u$ ]_인 경우 ${R_{\obega$ }} $=[\alpha]_$ {R_ ${\obega }}$ $\vert u\vert >\vert \alpha \vert$ u> $(\$ u $\vert$ >\ $vert$ \ $alpha \vert$ $[u]_{R_{\omega x}}=[\beta ]_{R_{\omega x}}$ 다음으로 [ $[u]_{R_{\omega x}}=[\beta ]_{R_{\omega x}}$ $[u]_{R_{\omega x}}=[\beta ]_{R_{\omega x}}$ $[u]_{R_{\omega x}}=[\beta ]_{R_{\omega x}}$ x $[u]_{R_{\omega x}}=[\beta ]_{R_{\omega x}}$ [ $[u]_{R_{\omega x}}=[\beta ]_{R_{\omega x}}$ R $[u]_{R_{\omega x}}=[\beta ]_{R_{\omega x}}$ \ $displaystyle [ u$ ] $[u]_{R_{\omega x}}=[\beta ]_{R_{\omega x}}$ ${R_{\obega$ x $}}=[\buff]_{R_{\obega$ x $[u]_{R_{\omega x}}=[\beta ]_{R_{\omega x}}$

$\alpha =\beta$ , $\alpha =\beta$ $\alpha =\beta$ β { $display style$ \ $alpha$ $=$ \display $\alpha =\beta$ }(예를 들어 $x$ { $displaystyle$ x $}$ 가 $\omega$ { $displaystyle \$ $alpha$ $\omega$ =\ $display$ =\ $varepsilon$ $}$ 에서 $\omega$ 전혀 발생하지 않은 $\alpha =\beta =\varepsilon$ )^[14]는 빈 오른쪽 컨텍스트에 $\alpha =\beta =\varepsilon$ 하는 $등가$ 분할된다는 것을 의미합니다 $.$

서픽스 링크 외에 오토마톤의 최종 상태를 정의하기 위해서도 필요합니다.구조 속성에서 $q=[\alpha ]_{R}$ [α $]$ $q=[\alpha ]_{R}$ {\ $displaystyle$ $\alpha$ q = $[\alpha$ ] $_$ ${$ R $q=[\alpha ]_{R}$ }에 $q=[\alpha ]_{R}$ 인식되는 $\alpha$ $α$ {\displaystyle $\$ $alpha$ }의 모든 접미사가 접미사 경로 $q, ink$ $(q), …)$ 의 $일부$ 정점에 의해 인식됩니다.즉, 길이가 $len(link(q))$ $len(link(q))$ $len(link(link(q))$ $len(link(q))$ n ( $len(link(q))$ $len(link(q))$ $len(link(q))$ $len(link(link(q))$ k ( $len(link(q))$ ){ $displaystyle len$ ( $len(link(link(q))$ ( $len(link(q))$ q )}{ $displaystyle$ $len(link(q))$ q $q$ }}{ displaystyle $len ($ $len(link(q))$ ( $len(link(link(q))$ $)}{$ $displaystyle$ $len(link(q))$ ( $($ )}}}{ displaystyle $len$ ( q $len(link(q))$ ) stylink ( $len(link(q))$ ( }}}}}보다 $len(link(link(q))$ 큰 접미사가 $있습니다$ . $link(q)$ ) { $displaystyle$ link $(q$ )} 등입니다 $link(q)$ . $\omega$ $"\displaystyle \opha"$ 를 $\omega$ 인식하는 상태가 l $t$ { $displaystyle$ last $}$ 로 표시되는 $경우$ 모든 최종 상태 $(\displaystyle$ \ $opha$ $}$ 의 서픽스를 인식하는 상태)가 시퀀스 $l$ $(last,link(last),link^{2}(last),\dots )$ $(last,link(last),link^{2}(last),\dots )$ $(last,link(last),link^{2}(last),\dots )$ $(last,link(last),link^{2}(last),\dots )$ k ( $(last,link(last),link^{2}(last),\dots )$ $(last,link(last),link^{2}(last),\dots )$ $(last,link(last),link^{2}(last),\dots )$ t $(last,link(last),link^{2}(last),\dots )$ ), $(last,link(last),link^{2}(last),\dots )$ $(last,link(last),link^{2}(last),\dots )$ $(last,link(last),link^{2}(last),\dots )$ 2 ( $(last,link(last),link^{2}(last),\dots )$ link $))를 형성$ 합니다. $ots$ ^[19]

전환 및 접미사 링크 업데이트

$\omega$ x(\ $displaystyle$ x $)$ 가 $x$ $"\displaystyle\obega"$ 에 $\omega$ 추가된 후 서픽스 자동화의 새로운 상태는 [ $[\omega x]_{R_{\omega x}}$ $[\omega x]_{R_{\omega x}}$ ] $[\omega x]_{R_{\omega x}}$ $[\omega x]_{R_{\omega x}}$ x {\ $displaystyle [\obega$ x] $_가$ 됩니다. ${R_{\obega$ x $}}$ $[\alpha ]_{R_{\omega x}}$ 및 [ $[\alpha ]_{R_{\omega x}}$ $[\alpha ]_{R_{\omega x}}$ $[\alpha ]_{R_{\omega x}}$ x {\ $displaystyle$ [\ $alpha ]_{R_{\obega$ x $[\alpha ]_{R_{\omega x}}$ [ $[\omega x]_{R_{\omega x}}$ x ] R $[\omega x]_{R_{\omega x}}$ x {\ $displaystyle [\obega$ x $]_$ }로부터의 $[\omega x]_{R_{\omega x}}$ 서픽스 링크{ $R_{\obega$ x $}}$ 는 $[\omega x]_{R_{\omega x}}$ [ $[\alpha ]_{R_{\omega x}}$ $[\alpha ]_{R_{\omega x}}$ $[\alpha ]_{R_{\omega x}}$ x $[\alpha ]_{R_{\omega x}}$ {\ $displaystyle$ $[\alpha$ $]_{$ $R_$ ${\obega$ x $}}$ 로 $[\alpha ]_{R_{\omega x}}$ $[\alpha ]_{R_{\omega x}}$ 하며 $[\alpha ]_{R_{\omega x}}$ [ $link([\alpha ]_{R_{\omega }})$ ] R $[\alpha ]_{R_{\omega x}}$ x {\ $display [\$ alpha $[\alpha ]_{R_{\omega x}}$ $]_{\obega$ x $}}$ 에서 $[\alpha ]_{R_{\omega x}}$ $[\alpha ]_{R_{\omega x}}$ $link([\alpha ]_{R_{\omega }})$ n $([$ ] $link([\alpha ]_{R_{\omega }})$ $link([\alpha ]_{R_{\omega }})$ 로 이동한다 $.$ { $R_{\obega$ x $}}$ 은 $[\omega x]_{R_{\omega x}}$ (는) 접미사로만 $\omega x$ {\ $displaystyle \obega$ x $}$ 에만 $\omega x$ 발생하므로 [ $[\omega x]_{R_{\omega x}}$ ] R $[\omega x]_{R_{\omega x}}$ {\ $displaystyle$ [\ $obega x$ _부터의 이행은 일절 없습니다 $.$ { $R_{\opha$ x $}}$ 은 $[\omega x]_{R_{\omega x}}$ (는) 길이가 $\alpha$ α $이상$ 인 $\omega$ {\ $displaystyle$ $\alpha$ $\omega$ $}$ 의 $\omega$ $\alpha$ 접미사에서 시작하여 문자 $x$ {\ $displaystyle$ x $x$ 로 표시해야 합니다 $[\alpha ]_{R_{\omega x}}$ [ $[\alpha ]_{R_{\omega x}}$ R $[\alpha ]_{R_{\omega x}}$ x $[\alpha ]_{R_{\omega x}}$ dis {\ $displaystyle [\alpha$ ] $_{\opha$ x $}$ 는 $[\alpha ]_{R_{\omega x}}$ $}$ 의 $[\alpha ]_{R_{\omega }}$ 서브셋으로 $[\alpha ]_{R_{\omega }}$ 됩니다. $laystyle [\alpha ]_$ {R_ ${\$ $obega$ $[\alpha ]_{R_{\omega }}$ $[\alpha ]_{R_{\omega x}}$ [ $[\alpha ]_{R_{\omega }}$ R $[\alpha ]_{R_{\omega x}}$ x {\ $displaystyle [\$ $alpha$ $]$ $_{\obe$ x $}$ 에서 $[\alpha ]_{R_{\omega x}}$ $[\alpha ]_{R_{\omega x}}$ [ $[\alpha ]_{R_{\omega x}}$ R $[\alpha ]_{R_{\omega }}$ {\ $display$ style $}$ 로 $[\alpha ]_{R_{\omega x}}$ 이행하는 것은 $[\alpha$ ] $[\alpha ]_{R_{\omega x}}$ $[\alpha ]_{R_{\omega x}}$ [\ $displaystyle$ ]에서와 같아야 $[\alpha ]_{R_{\omega x}}$ . ${\$ { $displaystyle$ \alpha $|\alpha |$ } $at$ less $len(link([\alpha ]_{R_{\omega }}))$ $len(link([\alpha ]_{R_{\omega }}))$ n ( $len(link([\alpha ]_{R_{\omega }}))$ k ( $len(link([\alpha ]_{R_{\omega }}))$ [ $len(link([\alpha ]_{R_{\omega }}))$ ] $)$ ) } $display len$ ( link ( [ \ $alpha ]_$ ${R$ _ { \ obega $[\alpha ]_{R_{\omega }}$ $len(link([\alpha ]_{R_{\omega }}))$ }} ){ $style$ $[\alpha ]_{R_{\omega }}$ len ( $link$ ( [ \ alpha ]_ ${\$ $alpha$ }) _ { \ } } } ） $len(link([\alpha ]_{R_{\omega }}))$ $）$ ω $[\alpha ]_{R_{\omega }}$ ω $ω$ $[\alpha ]_{R_{\omega }}$ ω ω ω ω ω $[\alpha ]_{R_{\omega }}$ ω ω ω ω ω [ ${\$ {\ $[\alpha ]_{R_{\omega }}$ [이 상태의 것.이러한 서픽스에 대응하는 상태는 [ $[\omega ]_{R_{\omega }}$ ${\$ \ $displaystyle$ [ \ $omega$ ] $_{R$ _ { \ omega $[\omega ]_{R_{\omega }}$ ^[19] $[\omega ]_{R_{\omega }}$ 의 서픽스 링크 패스의 트래버설로 판별할 수 있습니다.

단어 abbcbc에 대한 접미사 자동 생성

**∅ → a**

첫 번째 문자가 추가된 후에는 접미사 자동화로 하나의 상태만 생성됩니다.	마찬가지로 접미사 트리에 리프 하나만 추가됩니다.

**a → 복부**

이전에 b가 나타나지 않았기 때문에 이전의 모든 최종 상태에서 새로운 전환이 도출됩니다.	같은 이유로 접미사 트리의 루트에 다른 리프가 추가됩니다.

**ab → abb**

상태 2는 단어 ab와 b를 인식하지만 b만이 새로운 접미사이므로 이 단어는 상태 4로 구분됩니다.	접미사 트리에서 이는 정점 2로 이어지는 가장자리의 분할에 해당합니다.

**abb → abbc**

문자 c는 처음 발생하므로 이전의 모든 최종 상태에서 전이가 도출됩니다.	역문자열의 접미사 트리에 루트에 다른 리프가 추가되었습니다.

**abbc → abbcb**

상태 4는 유일한 단어 b(서픽스)로 구성되어 있기 때문에 상태는 분할되지 않습니다.	이에 대응하여 접미사목의 정점 4에 새로운 잎이 매달린다.

**abbcb → abbcbc**

상태 5는 단어 abbc, bbc, bc 및 c를 인식하지만 마지막 두 개만 새로운 단어의 접미사이므로 새 상태 8로 구분됩니다.	이에 대응하여 정점 5로 이어지는 엣지를 분할하고 엣지 중간에 정점 8을 둔다.

건설 알고리즘

상기의 이론적인 결과에 따라 $문자$ x(\ $displaystyle$ x)를 $x$ 사용하여 $\omega$ 자동화를 문자 x $(\displaystyle \omega$ ^[19]의 $\omega$ 서픽스 자동화로 재구축하는 알고리즘이 알고리즘은 다음과 같습니다.

$\omega$ $"\displaystyle\obega$ $last$ 에 $\omega$ 대응하는 상태는 l $a$ $s$ \ $displaystyle$ last로 $last$ 됩니다.
x $(\displaystyle$ x $)$ 가 $x$ 추가된 $후$ 이전 $값$ 인 $s$ t{ $displaystyle$ p $}$ 가 변수p ${\$ $displaystyle$ last}에 $last$ $p$ $last$ 되고 l t { $displaystyle$ last $}$ $자체$ 가 $last$ $\omega x$ x {\ $displaystyle \obe$ x $\omega x$ 에 대응하는 새로운 상태로 재할당됩니다.
$\omega$ 에 대응하는 $\omega$ 상태는 $l t$ $\omega$ \ $displaystyle$ last로 $last$ 하여 갱신됩니다 $.$ 이를 수행하려면 x $({displaystyle$ x $x$ 로 이미 이행한 상태가 될 때까지 $p,link(p),link^{2}(p),\dots$ p , $p,link(p),link^{2}(p),\dots$ $p,link(p),link^{2}(p),\dots$ k ( $p,link(p),link^{2}(p),\dots$ ) , $p,link(p),link^{2}(p),\dots$ $p,link(p),link^{2}(p),\dots$ $p,link(p),link^{2}(p),\dots$ 2 ( $p,link(p),link^{2}(p),\dots$ ) , $...$ { $display style$ p , $link$ （ $p$ ） , link ^ { $2}$ ( $p$ ) , \ $dots$ 를 $p,link(p),link^{2}(p),\dots$ 해야 합니다.
상기의 루프가 종료하면, 다음의 3개의 케이스가 있습니다.
1. 서픽스 경로 상에 x $(\displaystyle$ x $x$ 로 이행한 상태가 없는 $경우$ $\omega$ $(\displaystyle$ $x)$ 는 $x$ 이전에 \ $displaystyle$ \omega에서 $\omega$ 발생한 적이 없으며 $last$ 에서 $s$ (\ $displaystyle$ last $)$ 의 $last$ 서픽스 링크는 $q_{0}$ 로 이어집니다.
2. x $(\$ $displaystyle$ x $)$ 에 $x$ $의한$ $p$ 이행이 발견되어 l $len(p)+1=len(q)$ ( $len(p)+1=len(q)$ p $len(p)+1=len(q)$ ) + $len(p)+1=len(q)$ $len(p)+1=len(q)$ $len(p)+1=len(q)$ $len(p)+1=len(q)$ n ( $len(p)+1=len(q)$ ) ( \ $displaystyle$ $len(p)+1=len(q)$ len ( $p$ ) + 1 $= len$ ( $q$ ) $len(p)+1=len(q)$ $p$ 에서 $q$ (\ $displaystyle$ q $q$ 로 이어지는 경우 $,$ q { $displaystyle$ $q$ }는 $q$ 분할할 필요가 없습니다 $.$ $ast$
3. $len(q)>len(p)+1$ $len(q)>len(p)+1$ $len(p)+1$ ( $len(q)>len(p)+1$ ) $len(q)>len(p)+1$ > $len(q)>len(p)+1$ $len(q)>len(p)+1$ ( $len(q)>len(p)+1$ p ) $len(q)>len(p)+1$ + $len(q)>len(p)+1$ \ $display$ $style$ $len(p)+1$ (q ) $> len ($ p $)$ + 1 \ $display style$ len $(p$ $len(p)+1$ + $1$ \ $display style$ len ( p ) $cl$ ${\$ $len(p)+1$ from from $q$ from from from from from from from from from from from from from from from from from from from from from from from from from from from from from from from from from from from $from$ from from from from from from from from from from from from from from from from from from from from from from from from from from from from $from$ from from from l l l l l from from from
If the previous step was concluded with the creation of $cl$ , transitions from it and its suffix link should copy those of $q$ , at the same time $cl$ is assigned to be common suffix link of both $q$ and $last$ ;
Transitions that have led to $q$ before but corresponded to words of the length at most $len(p)+1$ are redirected to $cl$ . To do this, one continues going through the suffix path of $p$ until the state is found such that transition by $x$ from it doesn't lead to $q$ .

The whole procedure is described by the following pseudo-code:^[19]

function  $add_letter(x)$ :     define  $p = last$      assign  $last = new_state()$      assign  $len(last) = len(p) + 1$      while  $δ(p, x)$  is undefined:         assign  $δ(p, x) = last, p = link(p)$      define  $q = δ(p, x)$      if  $q = last$ :         assign  $link(last) = q 0$      else if  $len(q) = len(p) + 1$ :         assign  $link(last) = q$      else:         define  $cl = new_state()$          assign  $len(cl) = len(p) + 1$          assign  $δ(cl) = δ(q), link(cl) = link(q)$          assign  $link(last) = link(q) = cl$          while  $δ(p, x) = q$ :             assign  $δ(p, x) = cl, p = link(p)$

Here $q_{0}$ is the initial state of the automaton and $new\_state()$ is a function creating new state for it. It is assumed $last$ , $len$ , $link$ and $\delta$ are stored as global variables.^[19]

Complexity

Complexity of the algorithm may vary depending on the underlying structure used to store transitions of the automaton. It may be implemented in $O(n\log \Sigma )$ with $O(n)$ memory overhead or in $O(n)$ with $O(n \Sigma )$ memory overhead if one assumes that memory allocation is done in $O(1)$ . To obtain such complexity, one has to use the methods of amortized analysis. The value of $len(p)$ strictly reduces with each iteration of the cycle while it may only increase by as much as one after the first iteration of the cycle on the next add_letter call. Overall value of $len(p)$ never exceeds $n$ and it is only increased by one between iterations of appending new letters that suggest total complexity is at most linear as well. The linearity of the second cycle is shown in a similar way.^[19]

Generalizations

The suffix automaton is closely related to other suffix structures and substring indices. Given a suffix automaton of a specific string one may construct its suffix tree via compacting and recursive traversal in linear time.^[20] Similar transforms are possible in both directions to switch between the suffix automaton of $S$ and the suffix tree of reversed string $S^{R}$ .^[18] Other than this several generalizations were developed to construct an automaton for the set of strings given by trie,^[8] compacted suffix automation (CDAWG),^[7] to maintain the structure of the automaton on the sliding window,^[21] and to construct it in a bidirectional way, supporting the insertion of a characters to both the beginning and the end of the string.^[22]

Compacted suffix automaton

As was already mentioned above, a compacted suffix automaton is obtained via both compaction of a regular suffix automaton (by removing states which are non-final and have exactly one out-going arc) and the minimization of a suffix tree. Similarly to the regular suffix automaton, states of compacted suffix automaton may be defined in explicit manner. A two-way extension ${\overset {\scriptstyle {\longleftrightarrow }}{\gamma }}$ of a word $\gamma$ is the longest word $\omega =\beta \gamma \alpha$ , such that every occurrence of $\gamma$ in $S$ is preceded by $\beta$ and succeeded by $\alpha$ . In terms of left and right extensions it means that two-way extension is the left extension of the right extension or, which is equivalent, the right extension of the left extension, that is ${\textstyle {\overset {\scriptstyle \longleftrightarrow }{\gamma }}={\overset {\scriptstyle \leftarrow }{\overset {\rightarrow }{\gamma }}}={\overset {\rightarrow }{\overset {\scriptstyle \leftarrow }{\gamma }}}}$ . In terms of two-way extensions compacted automaton is defined as follows:^[15]

Theorem — Compacted suffix automaton of the word $S$ is defined by a pair $(V,E)$ , where:

$V=\{{\overleftrightarrow {\omega }}:\omega \in \Sigma ^{*}\}$ is a set of automaton states;
$E=\{({\overleftrightarrow {\omega }},x\alpha ,{\overleftrightarrow {\omega x}}):x\in \Sigma ,\alpha \in \Sigma ^{*},{\overleftrightarrow {\omega x}}={\overleftrightarrow {\omega }}x\alpha \}$ is a set of automaton transitions.

Two-way extensions induce an equivalence relation ${\textstyle {\overset {\scriptstyle \longleftrightarrow }{\alpha }}={\overset {\scriptstyle \longleftrightarrow }{\beta }}}$ which defines the set of words recognized by the same state of compacted automaton. This equivalence relation is a transitive closure of the relation defined by ${\textstyle ({\overset {\scriptstyle {\rightarrow }}{\alpha \,}}={\overset {\scriptstyle {\rightarrow }}{\beta \,}})\vee ({\overset {\scriptstyle {\leftarrow }}{\alpha }}={\overset {\scriptstyle {\leftarrow }}{\beta }})}$ , which highlights the fact that a compacted automaton may be obtained by both gluing suffix tree vertices equivalent via ${\overset {\scriptstyle {\leftarrow }}{\alpha }}={\overset {\scriptstyle {\leftarrow }}{\beta }}$ relation (minimization of the suffix tree) and gluing suffix automaton states equivalent via ${\overset {\scriptstyle {\rightarrow }}{\alpha \,}}={\overset {\scriptstyle {\rightarrow }}{\beta \,}}$ relation (compaction of suffix automaton).^[23] If words $\alpha$ and $\beta$ have same right extensions, and words $\beta$ and $\gamma$ have same left extensions, then cumulatively all strings $\alpha$ , $\beta$ and $\gamma$ have same two-way extensions. At the same time it may happen that neither left nor right extensions of $\alpha$ and $\gamma$ coincide. As an example one may take $S=\beta =ab$ , $\alpha =a$ and $\gamma =b$ , for which left and right extensions are as follows: ${\overset {\scriptstyle {\rightarrow }}{\alpha \,}}={\overset {\scriptstyle {\rightarrow }}{\beta \,}}=ab={\overset {\scriptstyle {\leftarrow }}{\beta }}={\overset {\scriptstyle {\leftarrow }}{\gamma }}$ , but ${\overset {\scriptstyle {\rightarrow }}{\gamma \,}}=b$ and ${\overset {\scriptstyle {\leftarrow }}{\alpha }}=a$ . That being said, while equivalence relations of one-way extensions were formed by some continuous chain of nested prefixes or suffixes, bidirectional extensions equivalence relations are more complex and the only thing one may conclude for sure is that strings with the same two-way extension are substrings of the longest string having the same two-way extension, but it may even happen that they don't have any non-empty substring in common. The total number of equivalence classes for this relation does not exceed $n+1$ which implies that compacted suffix automaton of the string having length $n$ has at most $n+1$ states. The amount of transitions in such automaton is at most $2n-2$ .^[15]

Suffix automaton of several strings

Consider a set of words $T=\{S_{1},S_{2},\dots ,S_{k}\}$ . It is possible to construct a generalization of suffix automaton that would recognize the language formed up by suffixes of all words from the set. Constraints for the number of states and transitions in such automaton would stay the same as for a single-word automaton if you put $n= S_{1} + S_{2} +\dots + S_{k}$ .^[23] The algorithm is similar to the construction of single-word automaton except instead of $last$ state, function add_letter would work with the state corresponding to the word $\omega _{i}$ assuming the transition from the set of words $\{\omega _{1},\dots ,\omega _{i},\dots ,\omega _{k}\}$ to the set $\{\omega _{1},\dots ,\omega _{i}x,\dots ,\omega _{k}\}$ .^[24]^[25]

This idea is further generalized to the case when $T$ is not given explicitly but instead is given by a prefix tree with $Q$ vertices. Mohri et al. showed such an automaton would have at most $2Q-2$ and may be constructed in linear time from its size. At the same time, the number of transitions in such automaton may reach $O(Q \Sigma )$ , for example for the set of words $T=\{\sigma _{1},a\sigma _{1},a^{2}\sigma _{1},\dots ,a^{n}\sigma _{1},a^{n}\sigma _{2},\dots ,a^{n}\sigma _{k}\}$ over the alphabet $\Sigma =\{a,\sigma _{1},\dots ,\sigma _{k}\}$ the total length of words is equal to ${\textstyle O(n^{2}+nk)}$ , the number of vertices in corresponding suffix trie is equal to $O(n+k)$ and corresponding suffix automaton is formed of $O(n+k)$ states and $O(nk)$ transitions. Algorithm suggested by Mohri mainly repeats the generic algorithm for building automaton of several strings but instead of growing words one by one, it traverses the trie in a breadth-first search order and append new characters as it meet them in the traversal, which guarantees amortized linear complexity.^[26]

Sliding window

Some compression algorithms, such as LZ77 and RLE may benefit from storing suffix automaton or similar structure not for the whole string but for only last $k$ its characters while the string is updated. This is because compressing data is usually expressively large and using $O(n)$ memory is undesirable. In 1985, Janet Blumer developed an algorithm to maintain a suffix automaton on a sliding window of size $k$ in $O(nk)$ worst-case and $O(n\log k)$ on average, assuming characters are distributed independently and uniformly. She also showed $O(nk)$ complexity cannot be improved: if one considers words construed as a concatenation of several $(ab)^{m}c(ab)^{m}d$ words, where $k=6m+2$ , then the number of states for the window of size $k$ would frequently change with jumps of order $m$ , which renders even theoretical improvement of $O(nk)$ for regular suffix automata impossible.^[27]

The same should be true for the suffix tree because its vertices correspond to states of the suffix automaton of the reversed string but this problem may be resolved by not explicitly storing every vertex corresponding to the suffix of the whole string, thus only storing vertices with at least two out-going edges. A variation of McCreight's suffix tree construction algorithm for this task was suggested in 1989 by Edward Fiala and Daniel Greene;^[28] several years later a similar result was obtained with the variation of Ukkonen's algorithm by Jesper Larsson.^[29]^[30] The existence of such an algorithm, for compacted suffix automaton that absorbs some properties of both suffix trees and suffix automata, was an open question for a long time until it was discovered by Martin Senft and Tomasz Dvorak in 2008, that it is impossible if the alphabet's size is at least two.^[31]

One way to overcome this obstacle is to allow window width to vary a bit while staying $O(k)$ . It may be achieved by an approximate algorithm suggested by Inenaga et al. in 2004. The window for which suffix automaton is built in this algorithm is not guaranteed to be of length $k$ but it is guaranteed to be at least $k$ and at most $2k+1$ while providing linear overall complexity of the algorithm.^[32]

Applications

Suffix automaton of the string $S$ may be used to solve such problems as:^[33]^[34]

Counting the number of distinct substrings of $S$ in $O( S )$ on-line,
Finding the longest substring of $S$ occurring at least twice in $O( S )$ ,
Finding the longest common substring of $S$ and $T$ in $O( T )$ ,
Counting the number of occurrences of $T$ in $S$ in $O( T )$ ,
Finding all occurrences of $T$ in $S$ in $O( T +k)$ , where $k$ is the number of occurrences.

It is assumed here that $T$ is given on the input after suffix automaton of $S$ is constructed.^[33]

Suffix automata are also used in data compression,^[35] music retrieval^[36]^[37] and matching on genome sequences.^[38]

References

^ ^a ^b Crochemore, Vérin (1997), p. 192
^ ^a ^b Weiner (1973)
^ Pratt (1973)
^ Slisenko (1983)
^ Blumer et al. (1984), p. 109
^ Chen, Seiferas (1985), p. 97
^ ^a ^b Blumer et al. (1987), p. 578
^ ^a ^b Inenaga et al. (2001), p. 1
^ ^a ^b Crochemore, Hancart (1997), pp. 3–6
^ ^a ^b Серебряков и др. (2006), pp. 50–54
^ Рубцов (2019), pp. 89–94
^ Hopcroft, Ullman (1979), pp. 65–68
^ ^a ^b Blumer et al. (1984), pp. 111–114
^ ^a ^b ^c ^d ^e ^f ^g ^h Crochemore, Hancart (1997), pp. 27–31
^ ^a ^b ^c ^d ^e ^f ^g Inenaga et al. (2005), pp. 159–162
^ Rubinchik, Shur (2018), pp. 1–2
^ Inenaga et al. (2005), pp. 156–158
^ ^a ^b ^c Fujishige et al. (2016), pp. 1–3
^ ^a ^b ^c ^d ^e ^f ^g Crochemore, Hancart (1997), pp. 31–36
^ Паращенко (2007), pp. 19–22
^ Blumer (1987), p. 451
^ Inenaga (2003), p. 1
^ ^a ^b Blumer et al. (1987), pp. 585–588
^ Blumer et al. (1987), pp. 588–589
^ Blumer et al. (1987), p. 593
^ Mohri et al. (2009), pp. 3558–3560
^ Blumer (1987), pp. 461–465
^ Fiala, Greene (1989), p. 490
^ Larsson (1996)
^ Brodnik, Jekovec (2018), p. 1
^ Senft, Dvořák (2008), p. 109
^ Inenaga et al. (2004)
^ ^a ^b Crochemore, Hancart (1997), pp. 36–39
^ Crochemore, Hancart (1997), pp. 39–41
^ Yamamoto et al. (2014), p. 675
^ Crochemore et al. (2003), p. 211
^ Mohri et al. (2009), p. 3553
^ Faro (2016), p. 145

Bibliography

Anselm Cyril Blumer; Janet Blumer; Andrzej Ehrenfeucht; David Haussler; Ross McConnell (1984). Building the minimal DFA for the set of all subwords of a word on-line in linear time. International Colloquium on Automata, Languages and Programming. pp. 109–118. doi:10.1007/3-540-13345-3_9. ISBN 978-3-540-13345-2. Wikidata Q90309073.
Anselm Cyril Blumer; Janet Blumer; Andrzej Ehrenfeucht; David Haussler; Ross McConnell (July 1987). "Complete inverted files for efficient text retrieval and analysis". Journal of the ACM. 34 (3): 578–595. CiteSeerX 10.1.1.87.6824. doi:10.1145/28869.28873. ISSN 0004-5411. Wikidata Q90311855.
Janet Blumer (December 1987). "How much is that DAWG in the window? A moving window algorithm for the directed acyclic word graph". Journal of Algorithms. 8 (4): 451–469. doi:10.1016/0196-6774(87)90045-9. ISSN 0196-6774. Wikidata Q90327976.
Andrej Brodnik; Matevž Jekovec (3 August 2018). "Sliding Suffix Tree". Algorithms. 11 (8): 118. doi:10.3390/A11080118. ISSN 1999-4893. Wikidata Q90431196.
Mu-Tian Chen; Joel Seiferas (1985). Efficient and Elegant Subword-Tree Construction. Combinatorial Algorithms on Words. pp. 97–107. CiteSeerX 10.1.1.632.4. doi:10.1007/978-3-642-82456-2_7. ISBN 978-3-642-82456-2. Wikidata Q90329833.
Maxime Crochemore; Christophe Hancart (1997). Automata for Matching Patterns. Handbook of Formal Languages. Vol. 2. pp. 399–462. CiteSeerX 10.1.1.392.8637. doi:10.1007/978-3-662-07675-0_9. ISBN 978-3-642-59136-5. Wikidata Q90413384.
Maxime Crochemore; Renaud Vérin (1997). On compact directed acyclic word graphs. Structures in Logic and Computer Science. Lecture Notes in Computer Science. pp. 192–211. CiteSeerX 10.1.1.13.6892. doi:10.1007/3-540-63246-8_12. ISBN 978-3-540-69242-3. Wikidata Q90413885.
Maxime Crochemore; Costas S. Iliopoulos; Gonzalo Navarro; Yoan J. Pinzon (2003). A Bit-Parallel Suffix Automaton Approach for (δ,γ)-Matching in Music Retrieval. International Symposium on String Processing and Information Retrieval. pp. 211–223. CiteSeerX 10.1.1.8.533. doi:10.1007/978-3-540-39984-1_16. ISBN 978-3-540-39984-1. Wikidata Q90414195.
Vladimir Serebryakov; Maksim Pavlovich Galochkin; Meran Gabibullaevich Furugian; Dmitriy Ruslanovich Gonchar (2006). Теория и реализация языков программирования: Учебное пособие (PDF) (in Russian). Moscow: MZ Press. ISBN 5-94073-094-9. Wikidata Q90432456.
Simone Faro (2016). Evaluation and Improvement of Fast Algorithms for Exact Matching on Genome Sequences. International Conference on Algorithms for Computational Biology. Lecture Notes in Computer Science. pp. 145–157. doi:10.1007/978-3-319-38827-4_12. ISBN 978-3-319-38827-4. Wikidata Q90412338.
Edward R. Fiala; Daniel H. Greene (April 1989). "Data compression with finite windows". Communications of the ACM. 32 (4): 490–505. doi:10.1145/63334.63341. ISSN 0001-0782. Wikidata Q90425560.
Yuta Fujishige; Yuki Tsujimaru; Shunsuke Inenaga; Hideo Bannai; Masayuki Takeda (2016). Computing DAWGs and Minimal Absent Words in Linear Time for Integer Alphabets (PDF). International Symposium on Mathematical Foundations of Computer Science. Vol. 58. pp. 38:1–38:14. doi:10.4230/LIPICS.MFCS.2016.38. ISBN 978-3-95977-016-3. ISSN 1868-8969. Wikidata Q90410044.
John Edward Hopcroft; Jeffrey David Ullman (1979). Introduction to Automata Theory, Languages, and Computation (1st ed.). Massachusetts: Addison-Wesley. ISBN 978-81-7808-347-6. OL 9082218M. Wikidata Q90418603.
Shunsuke Inenaga (March 2003). "Bidirectional Construction of Suffix Trees" (PDF). Nordic Journal of Computing. 10 (1): 52–67. CiteSeerX 10.1.1.100.8726. ISSN 1236-6064. Wikidata Q90335534.
Shunsuke Inenaga; Hiromasa Hoshino; Ayumi Shinohara; Masayuki Takeda; Setsuo Arikawa; Giancarlo Mauri; Giulio Pavesi (March 2005). "On-line construction of compact directed acyclic word graphs". Discrete Applied Mathematics. 146 (2): 156–179. CiteSeerX 10.1.1.1039.6992. doi:10.1016/J.DAM.2004.04.012. ISSN 0166-218X. Wikidata Q57518591.
Shunsuke Inenaga; Hiromasa Hoshino; Ayumi Shinohara; Masayuki Takeda; Setsuo Arikawa (2001). "Construction of the CDAWG for a trie" (PDF). Prague Stringology Conference. Proceedings: 37–48. CiteSeerX 10.1.1.24.2637. Wikidata Q90341606.
Shunsuke Inenaga; Ayumi Shinohara; Masayuki Takeda; Setsuo Arikawa (March 2004). "Compact directed acyclic word graphs for a sliding window". Journal of Discrete Algorithms. 2 (1): 33–51. CiteSeerX 10.1.1.101.358. doi:10.1016/S1570-8667(03)00064-9. ISSN 1570-8667. Wikidata Q90345535.
N. Jesper Larsson (1996). "Extended application of suffix trees to data compression". Proceedings. Data Compression Conference: 190–199. CiteSeerX 10.1.1.12.8623. doi:10.1109/DCC.1996.488324. ISSN 2375-0383. Wikidata Q90427112.
Mehryar Mohri; Pedro Moreno; Eugene Weinstein (September 2009). "General suffix automaton construction algorithm and space bounds". Theoretical Computer Science. 410 (37): 3553–3562. CiteSeerX 10.1.1.157.7443. doi:10.1016/J.TCS.2009.03.034. ISSN 0304-3975. Wikidata Q90410808.
Дмитрий А. Паращенко (2007), Обработка строк на основе суффиксных автоматов (PDF) (in Russian), Saint Petersburg: ITMO University, Wikidata Q90436837
Vaughan Ronald Pratt (1973), Improvements and applications for the Weiner repetition finder, OCLC 726598262, Wikidata Q90300966
Александр Александрович Рубцов (2019). Заметки и задачи о регулярных языках и конечных автоматах (PDF) (in Russian). Moscow: Moscow Institute of Physics and Technology. ISBN 978-5-7417-0702-9. Wikidata Q90435728.
Mikhail Rubinchik; Arseny M. Shur (February 2018). "Eertree: An efficient data structure for processing palindromes in strings" (PDF). European Journal of Combinatorics. 68: 249–265. arXiv:1506.04862. doi:10.1016/J.EJC.2017.07.021. ISSN 0195-6698. Wikidata Q90726647.
Martin Senft; Tomáš Dvořák (2008). Sliding CDAWG Perfection. International Symposium on String Processing and Information Retrieval. pp. 109–120. doi:10.1007/978-3-540-89097-3_12. ISBN 978-3-540-89097-3. Wikidata Q90426624.
Anatoly Olesievich Slisenko (1983). "Detection of periodicities and string-matching in real time". Journal of Mathematical Sciences. 22 (3): 1316–1387. doi:10.1007/BF01084395. ISSN 1072-3374. Wikidata Q90305414.
Peter Weiner (October 1973). "Linear pattern matching algorithms". Symposium on Foundations of Computer Science: 1–11. CiteSeerX 10.1.1.474.9582. doi:10.1109/SWAT.1973.13. Wikidata Q29541479.
Jun'ichi Yamamoto; Tomohiro I; Hideo Bannai; Shunsuke Inenaga; Masayuki Takeda (2014). Faster Compact On-Line Lempel-Ziv Factorization (PDF). Symposium on Theoretical Aspects of Computer Science. Leibniz International Proceedings in Informatics. Vol. 25. pp. 675–686. CiteSeerX 10.1.1.742.6691. doi:10.4230/LIPICS.STACS.2014.675. ISBN 978-3-939897-65-1. ISSN 1868-8969. Wikidata Q90348192.

External links

Media related to Suffix automaton at Wikimedia Commons
Suffix automaton article on E-Maxx Algorithms in English

[:16-1] Crochemore, Vérin (1997), p. 192

[:5-2] Weiner (1973)

[3] Pratt (1973)

[4] Slisenko (1983)

[:2-5] Blumer et al. (1984), p. 109

[:6-6] Chen, Seiferas (1985), p. 97

[:7-7] Blumer et al. (1987), p. 578

[:8-8] Inenaga et al. (2001), p. 1

[:1-9] Crochemore, Hancart (1997), pp. 3–6

[:14-10] Серебряков и др. (2006), pp. 50–54

[11] Рубцов (2019), pp. 89–94

[12] Hopcroft, Ullman (1979), pp. 65–68

[:9-13] Blumer et al. (1984), pp. 111–114

[:10-14] ^ ^a ^b ^c ^d ^e ^f ^g ^h Crochemore, Hancart (1997), pp. 27–31

[:3-15] ^ ^a ^b ^c ^d ^e ^f ^g Inenaga et al. (2005), pp. 159–162

[16] Rubinchik, Shur (2018), pp. 1–2

[:0-17] Inenaga et al. (2005), pp. 156–158

[:11-18] Fujishige et al. (2016), pp. 1–3

[:12-19] ^ ^a ^b ^c ^d ^e ^f ^g Crochemore, Hancart (1997), pp. 31–36

[20] Паращенко (2007), pp. 19–22

[21] Blumer (1987), p. 451

[22] Inenaga (2003), p. 1

[:13-23] Blumer et al. (1987), pp. 585–588

[24] Blumer et al. (1987), pp. 588–589

[25] Blumer et al. (1987), p. 593

[26] Mohri et al. (2009), pp. 3558–3560

[27] Blumer (1987), pp. 461–465

[28] Fiala, Greene (1989), p. 490

[29] Larsson (1996)

[30] Brodnik, Jekovec (2018), p. 1

[31] Senft, Dvořák (2008), p. 109

[32] Inenaga et al. (2004)

[:15-33] Crochemore, Hancart (1997), pp. 36–39

[:4-34] Crochemore, Hancart (1997), pp. 39–41

[35] Yamamoto et al. (2014), p. 675

[36] Crochemore et al. (2003), p. 211

[37] Mohri et al. (2009), p. 3553

[38] Faro (2016), p. 145

[3]

[4]

[5]

[2]

[6]

[7]

[1]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

v t Strings
String metric	Approximate string matching Bitap algorithm Damerau–Levenshtein distance Edit distance Gestalt Pattern Matching Hamming distance Jaro–Winkler distance Lee distance Levenshtein automaton Levenshtein distance Wagner–Fischer algorithm
String-searching algorithm	Apostolico–Giancarlo algorithm Boyer–Moore string-search algorithm Boyer–Moore–Horspool algorithm Knuth–Morris–Pratt algorithm Rabin–Karp algorithm
Multiple string searching	Aho–Corasick Commentz-Walter algorithm
Regular expression	Comparison of regular-expression engines Regular grammar Thompson's construction Nondeterministic finite automaton
Sequence alignment	Hirschberg's algorithm Needleman–Wunsch algorithm Smith–Waterman algorithm
Data structure	DAFSA Suffix array Suffix automaton Suffix tree Generalized suffix tree Rope Ternary search tree Trie
Other	Parsing Pattern matching Compressed pattern matching Longest common subsequence Longest common substring Sequential pattern mining Sorting

Search