톰슨 구조

컴퓨터 과학에서 톰슨의 구성 알고리즘은 맥노튼-야마다라고도 불린다.톰슨 ^[1]알고리즘은 정규식을 동등한 비결정론적 유한 오토마톤(NFA)^[2]으로 변환하는 방법입니다.이 NFA를 사용하여 문자열을 정규 표현과 일치시킬 수 있습니다.이 알고리즘은 Ken Thompson에 의해 인정됩니다.

정규 표현과 비결정적 유한 오토마타는 형식 언어의 두 가지 표현이다.예를 들어 텍스트 처리 유틸리티는 고급 검색 패턴을 설명하기 위해 정규 표현을 사용하지만 NFA는 컴퓨터에서 실행하기에 더 적합합니다.따라서 이 알고리즘은 정규 표현을 NFA로 컴파일할 수 있기 때문에 실용적으로 중요합니다.이론적인 관점에서 보면, 이 알고리즘은 두 알고리즘이 정확히 같은 언어, 즉 일반 언어를 받아들인다는 증거의 일부입니다.

NFA는 파워셋 구성에 의해 결정론적으로 된 후 주어진 정규식에 대응하는 최적의 오토마톤을 얻기 위해 최소화할 수 있다.단, NFA는 직접 해석할 수도 있습니다.

주어진 두 정규식이 동일한 언어를 기술하는지 여부를 결정하기 위해, 각각은 톰슨의 구성, 파워셋 구성 및 DFA 최소화를 통해 동등한 최소 결정론적 유한 오토마톤으로 변환될 수 있다.결과 자동타가 상태 이름 변경에 동의하는 경우에만 정규 표현의 언어가 일치합니다.

알고리즘

알고리즘은 식을 구성 하위 표현식으로 분할하여 재귀적으로 작동합니다. 여기서 ^[3]규칙 집합을 사용하여 NFA가 구성됩니다.보다 정확하게는 $정규식$ E에서 전이함수 $δ$ 를^{[clarification needed]} 갖는 $오토마톤$ A는 다음과 같은 성질을 가진다.

A에는 다른 $상태$ 에서는₀ 액세스할 수 없는 초기 상태q가 1개만 $있습니다$ 즉, 임의의 $상태q$ 및 임의의 $\Delta (q,a)$ )에 $\Delta (q,a)$ { $displaystyle \Delta(q,a)}$ 에는 ${\displaystyle\Delta(q,a)}$ $\Delta (q,a)$ q가 $포함$ 되어₀ 있지 않습니다.
$A$ 에는 다른 $상태$ 에서는_f 공존할 수 없는 최종 상태q가1개 있어요즉, 임의의 $문자$ a에 $\Delta (q_{f},a)=\emptyset$ a) $= "\displaystyle \Delta (q_{f},a$ )=\ $emptyset$ 입니다.
$c$ 는 정규 $표현$ E의 연결 수, 괄호 이외의 기호 수(즉 $,$ , $*,$ $a$ 및 $ε$ )로 합니다.A의 $상태$ 수는 $2s$ - $c$ ( $E$ 의 크기에서 선형)이다.
임의의 스테이트에서 탈퇴하는 트랜지션의 수는 최대 2개입니다.
$m상태$ 의 NFA 및 각 $상태$ 로부터의 최대e의 천이는 $시간$ O $(emn)$ 의 $길이n$ 문자열과 일치할 수 있기 때문에 Thompson NFA는 고정사이즈 ^[4]^{[better source needed]}알파벳을 가정하여 선형시간 내에 패턴 매칭을 실행할 수 있습니다.

규칙.

아호 등에 따르면 다음과 같은 규칙이 설명된다.(2007),^[1] 페이지 122.여기서 N(s)과 N(t)은 각각 서브식 s 및 t의 NFA이다.

empty-expression is는 로 변환됩니다.

입력 알파벳 기호 a는 다음과 같이 변환됩니다.

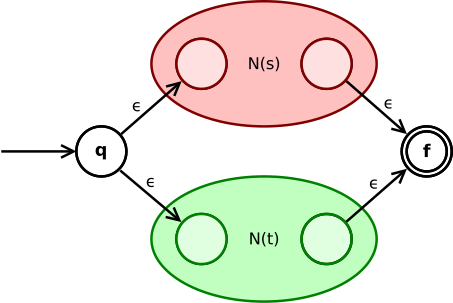
결합식의 t는 다음과 같이 변환됩니다.

상태 q는 를 경유하여 N(s) 또는 N(t)의 초기 상태로 이행합니다.이들의 최종 상태는 전체 NFA의 중간 상태가 되고 두 번의 δ 전환을 통해 NFA의 최종 상태로 병합된다.

연결식 st는 다음과 같이 변환됩니다.

N의 초기 상태는 전체 NFA의 초기 상태입니다.N(s)의 최종 상태가 N(t)의 초기 상태가 됩니다.N(t)의 최종 상태는 전체 NFA의 최종 상태입니다.

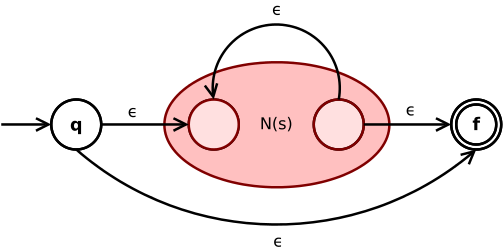
클린별 표현은^* 다음과 같이 변환됩니다.

γ-천이는 NFA의 초기 상태와 최종 상태를 서브 NFA N(s)과 사이에 접속한다.N(s)의 내부 최종 상태에서 내부 초기 상태로의 또 다른 γ-전이 별 연산자에 따른 식 s의 반복을 가능하게 한다.

괄호 안의 식(s)은 N개 자체로 변환됩니다.

이러한 규칙을 사용하면 빈 식 및 기호 규칙을 기본 사례로 사용하여 정규식이 동등한 ^[1]NFA로 변환될 수 있음을 수학적 귀납으로 증명할 수 있습니다.

예

이제 두 가지 예를 제시합니다. 결과가 포함된 비공식적인 예와 알고리즘의 단계별 적용을 포함하는 큰 예입니다.

작은 예

의 예(ε a*b)톰슨의 구조를 사용하여 단계별로

아래 사진은 톰슨의 건설 결과를 보여준다.(ε a*b)보라색 타원형은 a, 청록색 타원형은 a*, 녹색 타원형은 b, 주황색 타원형은 a*b, 파란색 타원형은 ε에 해당합니다.

알고리즘의 적용

정규 표현에서 얻은 NFA(0 (1(01*(00)*0)*1)*)*

예를 들어, 그림은 3의 배수인 이진수 집합을 나타내는 정규식에 대한 톰슨의 구성 알고리즘의 결과를 보여준다.

{ ,, "0", "00", "11", "000", "011", "110", "0000", "0011", "0110", "1001", "11", "11", "00000", ...}.

오른쪽 상단에는 표현의 논리 구조(구문 트리)가 표시되며, 연결(변수 특성 포함)을 나타냅니다. 하위 표현식은 참조를 위해 a-q로 명명됩니다.왼쪽 부분은 톰슨 알고리즘에 의해 생성된 비결정론적 유한 오토마톤을 나타내며, 각 하위 표현의 시작 상태와 종료 상태는 각각 자홍색과 시안으로 색칠된다.알기 쉽게 하기 위해 as transition label은 생략합니다.라벨이 붙어 있지 않은 이행은 실제로는 trans 이행입니다.루트식 q에 대응하는 엔트리 스테이트와 종료 스테이트는 각각 자동의 시작 스테이트와 수락 스테이트입니다.

알고리즘의 순서는 다음과 같습니다.

질문:	클린 별의 발현 변환을 개시하다									`(0 (1(01(00)0)1))*`
	b:	유니언 식 변환을 개시하다								`0 (1(01(00)0)1)`
		a:	변환 기호							`0`
		p:	클린 별의 발현 변환을 개시하다							`(1(01(00)0)1)`
			d:	연결식 변환 시작						`1(01(00)0)*1`
				c:	변환 기호					`1`
				n:	클린 별의 발현 변환을 개시하다					`(01(00)0)*`
					f:	연결식 변환 시작				`01(00)0`
						e:	변환 기호			`0`
						h:	클린 별의 발현 변환을 개시하다			`1*`
							g:	변환 기호		`1`
						h:	Kleene 별 표현 변환을 완료했습니다.			`1*`
						l:	클린 별의 발현 변환을 개시하다			`(00)*`
							j:	연결식 변환 시작		`00`
								i:	변환 기호	`0`
								k:	변환 기호	`0`
							j:	연결 식 변환이 완료되었습니다.		`00`
						l:	Kleene 별 표현 변환을 완료했습니다.			`(00)*`
						m:	변환 기호			`0`
					f:	연결 식 변환이 완료되었습니다.				`01(00)0`
				n:	Kleene 별 표현 변환을 완료했습니다.					`(01(00)0)*`
				o:	변환 기호					`1`
			d:	연결 식 변환이 완료되었습니다.						`1(01(00)0)*1`
		p:	Kleene 별 표현 변환을 완료했습니다.							`(1(01(00)0)1)`
	b:	유니언 식 변환을 완료했습니다.								`0 (1(01(00)0)1)`
질문:	Kleene 별 표현 변환을 완료했습니다.									`(0 (1(01(00)0)1))*`

등가 최소 결정론적 오토마톤을 아래에 나타냅니다.

다른 알고리즘과의 관계

Thompson's는 정규 ^[5]표현에서 NFA를 구성하는 여러 알고리즘 중 하나입니다. 이전의 알고리즘은 McNaughton과 ^[6]Yamada에 의해 제공되었습니다.톰슨의 구조와 반대로, 클린의 알고리즘은 유한 오토마톤을 정규식으로 변환합니다.

글루시코프의 구성 알고리즘은 θ-전이 제거되면 톰슨의 구성과 유사합니다.

레퍼런스

^ ^a ^b ^c Alfred Vaino Aho; Monica S. Lam; Ravi Sethi; Jeffrey D. Ullman (2007). "3.7.4 Construction of an NFA from a Regular Expression" (print). Compilers : Principles, Techniques, & Tools (2nd ed.). Boston, MA, USA: Pearson Addison-Wesley. p. 159–163. ISBN 9780321486813.
^ Louden, Kenneth C. (1997). "2.4.1 From a Regular Expression to an NFA" (print). Compiler construction : Principles and Practice (3rd ed.). 20 Park Plaza Boston, MA 02116-4324, US: PWS Publishing Company. pp. 64–69. ISBN 978-0-534-93972-4.{{cite book}}: CS1 유지보수: 위치(링크)
^ Ken Thompson (Jun 1968). "Programming Techniques: Regular expression search algorithm". Communications of the ACM. 11 (6): 419–422. doi:10.1145/363347.363387. S2CID 21260384.
^ Xing, Guangming. "Minimized Thompson NFA" (PDF).
^ Watson, Bruce W. (1995). A taxonomy of finite automata construction algorithms (PDF) (Technical report). Eindhoven University of Technology. Computing Science Report 93/43.
^ R. McNaughton, H. Yamada (Mar 1960). "Regular Expressions and State Graphs for Automata". IEEE Transactions on Electronic Computers. 9 (1): 39–47. doi:10.1109/TEC.1960.5221603.

[DragonBook-1] Alfred Vaino Aho; Monica S. Lam; Ravi Sethi; Jeffrey D. Ullman (2007). "3.7.4 Construction of an NFA from a Regular Expression" (print). Compilers : Principles, Techniques, & Tools (2nd ed.). Boston, MA, USA: Pearson Addison-Wesley. p. 159–163. ISBN 9780321486813.

[2] Louden, Kenneth C. (1997). "2.4.1 From a Regular Expression to an NFA" (print). Compiler construction : Principles and Practice (3rd ed.). 20 Park Plaza Boston, MA 02116-4324, US: PWS Publishing Company. pp. 64–69. ISBN 978-0-534-93972-4.{{cite book}}: CS1 유지보수: 위치(링크)

[3] Ken Thompson (Jun 1968). "Programming Techniques: Regular expression search algorithm". Communications of the ACM. 11 (6): 419–422. doi:10.1145/363347.363387. S2CID 21260384.

[4] Xing, Guangming. "Minimized Thompson NFA" (PDF).

[5] Watson, Bruce W. (1995). A taxonomy of finite automata construction algorithms (PDF) (Technical report). Eindhoven University of Technology. Computing Science Report 93/43.

[6] R. McNaughton, H. Yamada (Mar 1960). "Regular Expressions and State Graphs for Automata". IEEE Transactions on Electronic Computers. 9 (1): 39–47. doi:10.1109/TEC.1960.5221603.

[1]

[2]

[3]

[4]

[5]

[6]

v t 줄들
문자열 메트릭	대략적인 문자열 매칭 비트맵 알고리즘 다메라우-레벤슈테인 거리 거리 편집 게스탈트 패턴 매칭 해밍 거리 자로-윙클러 거리 리 거리 레벤슈테인 오토마톤 레벤슈테인 거리 바그너-피셔 알고리즘
문자열 검색 알고리즘	사도-장칼로 알고리즘 Boyer-Moore 문자열 검색 알고리즘 보이어-무어-호스풀 알고리즘 크누스-모리스-프랫 알고리즘 라빈-카르프 알고리즘
다중 문자열 검색	아호코라식 Commentz-Walter 알고리즘
정규 표현	정규 표현 엔진 비교 정규 문법 톰슨 구조 비결정론적 유한 오토마톤
시퀀스 얼라인먼트	히르슈베르크 알고리즘 니들맨분쉬 알고리즘 스미스-워터맨 알고리즘
data 구조	DAFSA 서픽스 배열 서픽스 오토마톤 접미사 트리 일반 접미사 트리 출렁 삼원 검색 트리 트리
다른.	해석 패턴 매칭 압축 패턴 매칭 최장 공통 서브시퀀스 최장 공통 서브스트링 순차적 패턴 마이닝 정렬

Search