하겐-포이수일 방정식

시리즈의 일부
연속체역학
${\displaystyle J=-D{\frac {d\varphi}{dx}}$ 픽의 확산 법칙
법칙들 보수주의 덩어리 운동량 에너지 부등식 클라우지우스-두헴(엔트로피)
고체역학 변형 탄력성 선형의 가소성 훅의 법칙 스트레스 부담 유한 변형 극소 변형률 호환성. 굽힘 접촉역학 마찰의 재료파손론 파단역학
유체역학 유체 통계학 · 역학 아르키메데스의 원리 · 베르누이의 원리 나비에-스토크스 방정식 포이슈유 방정식 · 파스칼의 법칙 점성 (뉴턴어·비뉴턴어) 부력 · 믹싱 · 압력. 액체 접착력 모세관 작용 크로마토그래피 응집력(화학) 표면장력 가스 대기. 보일의 법칙 찰스의 법칙 결합기체법칙 픽의 법칙 Gay-Lussac's law 그레이엄의 법칙 플라스마
레올로지 점탄성 레오미터 레오미터 스마트 유체 전기신학 자기신학 페로플루이드
사이언티스트 베르누이 보일 코시 찰스 오일러 픽 게이뤼삭 그레이엄 훅 뉴턴 경이다. 나비에 놀 파스칼 스톡스 트루델
v t

비이상적 유체 역학에서 하겐-포이슈유 방정식, 즉 하겐-포이슈유 법칙, 포이슈유 법칙 또는 포이슈유 방정식은 일정한 단면의 긴 원통형 파이프를 흐르는 층류 흐름에서 비압축성 및 뉴턴 유체의 압력 강하를 제공하는 물리 법칙입니다. 폐 폐포의 공기 흐름이나 음용 빨대 또는 피하 바늘을 통한 흐름에 성공적으로 적용할 수 있습니다. 1838년^[1] 장 레오나르 마리 포이슈유(Jean Léonard Marie Poiseuille)와 1846년 고틸프 하인리히 루트비히 하겐(Gottilf Heinrich Ludwig Hagen)이 각각 실험적으로 도출하였으며,^[2] 1840~41년 포이슈유가 1846년에 출판하였습니다.^[1] 포이슈유 법칙의 이론적 정당성은 1845년 조지 스톡스에 의해 제시되었습니다.^[3]

이 방정식의 가정은 유체가 비압축성이고 뉴턴식이며, 흐름은 직경보다 훨씬 긴 일정한 원형 단면의 파이프를 통해 층류적이며, 파이프 내에 유체의 가속은 없다는 것입니다. 임계값 이상의 속도 및 파이프 직경의 경우 실제 유체 흐름은 층류가 아니라 난류이므로 Hagen-Poiseuille 방정식에 의해 계산된 것보다 더 큰 압력 강하로 이어집니다.

Poiseuille의 방정식은 유체의 점도로 인한 압력 강하를 설명합니다. 유체 내에서 다른 유형의 압력 강하가 여전히 발생할 수 있습니다(여기 시연 참조).^[4] 예를 들어, 점성 유체를 중력에 대항하여 위로 끌어올리는 데 필요한 압력은 포이슈유의 법칙에서 필요한 압력과 베르누이의 방정식에서 필요한 압력을 모두 포함하고 있으므로 흐름의 어떤 지점도 0보다 큰 압력을 가질 수 있습니다(그렇지 않으면 흐름이 일어나지 않습니다).

또 다른 예는 혈액이 좁은 수축 상태로 흐를 때 (체적 유속의 연속성으로 인해) 더 큰 직경보다 속도가 더 빨라지고 (베르누이^[4] 방정식으로 인해) 더 큰 직경보다 압력이 더 낮아진다는 것입니다. 그러나 혈액의 점도는 이동한^[4] 길이에 비례하는 흐름 방향을 따라 추가적인 압력 강하를 유발합니다(Poiseuille의 법칙에 따라). 두 효과 모두 실제 압력 강하에 기여합니다.

식

표준 유체 역학 표기법:^[5][6][7]

${\displaystyle \Delta p={\frac {8\mu LQ}{\pi R^{4}}}={\frac {8\pi \mu LQ}{A^{2}}},}$

어디에

δP는 양 끝 사이의 압력 차이입니다.

L은 파이프의 길이이고,

μ는 동적 점도이고,

Q는 체적 유량,

R은 파이프 반경이고,

A는 파이프의 단면적입니다.

방정식이 파이프 입구에 가까이 가지 않습니다.^{[8]: 3}

이 방정식은 낮은 점도, 넓은 파이프 및/또는 짧은 파이프의 한계에서 실패합니다. 점도가 낮거나 파이프가 넓으면 난류 흐름이 발생할 수 있으므로 Darcy-Weisbach 방정식과 같은 보다 복잡한 모델을 사용해야 합니다. Hagen-Poiseuille 법칙이 유효하려면 파이프의 길이 대 반지름의 비율이 레이놀즈 수의 1/48보다 커야 합니다.^[9] 파이프가 너무 짧으면 Hagen-Poiseuille 방정식은 비물리적으로 높은 유량을 초래할 수 있습니다. 흐름은 덜 제한적인 조건에서 Bernouli의 원리에 의해 경계지어집니다.

${\displaystyle {\begin{aligned}\Delta p={\frac {1}{2}}\rho {\overline {v}_{\text{max}}^{2}&={\frac {1}{2}\rho \left ({\frac {Q_{\text{max}}\right)^{2}\rho \displaystyle {\begin{aligned}\Delta p={\rho}}\rho {aligned}}\rho \left quad\frac {Q_{\text{max}}\right)^{2}\rho\end{aligned}}}$

비압축성 흐름에서는 절대적인 (게이지 압력과 혼동되지 않는) 압력을 가질 수 없기 때문입니다.

다아시-바이스바흐 방정식과의 관계

일반적으로 Hagen-Poiseuil 흐름은 위의 압력 강하에 대한 관계뿐만 아니라 포물선인 층류 프로파일에 대한 완전한 해결책을 의미합니다. 그러나, 난류 흐름에서의 유동 프로파일은 엄밀히 말하면 포물선이 아니지만, 난류 흐름의 경우 효과적인 난류 점도를 추론함으로써 압력 강하에 대한 결과를 난류 흐름으로 확장할 수 있습니다. 층류형이든 난류형이든 두 경우 모두 압력 강하는 벽의 응력과 관련이 있으며, 이는 소위 마찰 계수를 결정합니다. 벽 응력은 레이놀즈 수 측면에서 마찰 계수에 대한 관계가 주어진 수리학 분야에서 다아시-바이스바흐 방정식에 의해 현상학적으로 결정될 수 있습니다. 층류 흐름의 경우 원형 단면의 경우:

${\displaystyle \Lambda ={\frac {64}{\mathrm {Re}},\quad \mathrm {Re} ={\frac {\rhovd}{\mu}}$

여기서 Re는 Reynolds number, ρ는 유체 밀도, v는 평균 유속으로 층류의 경우 최대 유속의 절반입니다. 이 양은 난류 흐름의 경우에도 잘 정의되어 있는 반면, 최대 유속은 그렇지 않거나 어떤 경우에도 추론하기 어려울 수 있기 때문에 평균 유속의 관점에서 레이놀즈 수를 정의하는 것이 더 유용합니다. 이 형식에서 이 법칙은 원통형 튜브에서 매우 낮은 속도로 층류의 다아시 마찰 계수, 에너지(헤드) 손실 계수, 마찰 손실 계수 또는 다아시(마찰) 계수 λ를 근사합니다. 약간 다른 형태의 법칙의 이론적 파생은 1856년에 위드만과 노이만과 E에 의해 독립적으로 이루어졌습니다. 1858년 하겐바흐(1859, 1860). 하겐바흐는 이 법칙을 포이슈유의 법칙이라고 부른 첫 번째 사람입니다.

생리학의 두 분야인 혈액학과 혈역학에서도 법칙은 매우 중요합니다.^[10]

포이슈유의 법칙은 후에 1891년에 하겐바흐의 연구에 기초하여 L. R. 윌버포스에 의해 격동의 흐름으로 확장되었습니다.

파생

하겐-포이수일 방정식은 나비에로부터 유도될 수 있습니다.–스토크 방정식. 균일한(원형) 단면의 파이프를 통한 층류 흐름을 하겐-포이슈유 흐름이라고 합니다. 하겐-포이슈유 흐름을 지배하는 방정식은 나비에로부터 직접 유도될 수 있습니다.– 다음과 같은 가정을 수행하여 3D 원통 좌표(r, θ,x)에 운동량 방정식을 저장합니다.

1. 흐름이 안정적입니다( ∂.../∂t = 0 ).
2. 유체 속도의 반경 및 방위각 성분은 0(u = u = 0)입니다.
3. 흐름은 축대칭( ∂.../ ∂θ = 0)입니다.
4. 흐름이 완전히 전개됩니다( ∂u/ ∂x = 0). 그러나 여기서 이것은 질량 보존과 위의 가정을 통해 증명될 수 있습니다.

그러면 운동량 방정식의 각 방정식과 연속 방정식이 동일하게 만족됩니다. 반경 운동량 방정식은 ∂p/ ∂r = 0으로 감소합니다. 즉, 압력 p는 축 좌표 x만의 함수입니다. 간결함을 위해 ${\displaystyle {ux}_{}}$ ${\$ 대신 u를 사용합니다$.$ 축방향 운동량 방정식은 다음과 같이 감소합니다.

${\displaystyle {\frac {1}{r}}{\partial }{\partial r}}\left(r{\frac {\partial u}{\partial r}\right)={\frac {1}{\mu }}{\frac {\mathrm {d} p}{\mathrm {d} x}}}$

여기서 μ는 유체의 동적 점도입니다. 위의 식에서 좌변은 r의 함수이고 우변은 x의 함수일 뿐이므로 두 항이 동일해야 함을 의미합니다. 이 상수를 평가하는 것은 간단합니다. 파이프의 길이를 L로 하고 파이프의 양 끝 사이의 압력차를 δp(고압에서 저압을 뺀 값)로 표시하면 상수는 단순합니다.

${\displaystyle -{\frac {\mathrm {d} p}{\mathrm {d} x}}={\frac {\Delta p}{L}}=G}$

G가 양수가 되도록 정의했습니다. 해결책은.

${\displaystyle u=-{\frac {Gr^{2}}{4\mu }}+c_{1}\ln r+c_{2}}$

r = 0, c = 0에서 유한해야 하므로, 파이프 벽의 미끄럼 방지 경계 조건은 r = R(파이프의 radius)에서 u = 0이어야 하며, 이는 c = GR/4μ를 산출합니다. 따라서 우리는 마침내 다음과 같은 포물선 속도 프로파일을 갖게 됩니다.

${\displaystyle u={\frac {G}{4\mu }}\left(R^{2}-r^{2}\right).}$

최대 속도는 파이프 중심선(r = 0), u = GR/4μ에서 발생합니다. 파이프 단면을 적분하면 평균 속도를 얻을 수 있습니다.

${\displaystyle {u}_{\mathrm {avg} }={\frac {1}{\pi R^{2}}}\int _{0}^{R}2\pi ru\mathrm {d} r={\tfrac {1}{2}}{u}_{\mathrm {max} }.}$

실험에서 쉽게 측정할 수 있는 양은 체적 유량 Q = πRu입니다. 이를 재배열하면 Hagen-Poiseuille 방정식을 얻을 수 있습니다.

${\displaystyle \Delta p={\frac {8\mu QL}{\pi R^{4}}}.}$

배관내 포이세유 흐름 개시

긴 파이프의 양 끝 사이에 일정한 압력 구배 G = -dp/ dx을 적용하면 흐름이 즉시 포이세유 프로파일을 얻는 것이 아니라 시간이 지남에 따라 발전하여 정상 상태에서 포이세유 프로파일에 도달합니다. 나비에– 스톡 방정식은 다음으로 줄어듭니다.

${\displaystyle {\frac {\partial u}{\partial t}}={\frac {G}{\rho }}+\nu \left ({\frac {\partial ^{2}u}{\partial r^{2}}+{\frac {1}{r}{\frac {\partial u}{\partial r}}\right)}$

초기 및 경계 조건에서,

${\displaystyle u(r,0)=0,\quad u(R,t)=0.}$

속도 분포는 다음과 같습니다.

${\displaystyle u(r,t)={\frac {G}{4\mu }}\left(R^{2}-r^{2}\right)-{\frac {2GR^{2}}{\mu }}\sum _{n=1}^{\infty }{\frac {1}{\lambda _{n}^{3}}}{\frac {J_{0}(\lambda _{n}r/R)}{J_{1}(\lambda _{n})}}e^{-\lambda _{n}^{2}\nu t/R^{2}},\quad J_{0}\left(\lambda _{n}\right)=0}$

여기서 J(λr/R)는 첫 번째 종류의 차수 0의 베셀 함수이고 λ는 이 함수의 양의 근이며 J(λ)는 첫 번째 종류의 차수 1의 베셀 함수입니다. t → ∞로 Poiseuille 용액을 회수합니다.

고리형 단면의 포이세유 흐름

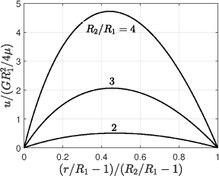
R이₁ 내부 실린더 반지름이고₂ R이 외부 실린더 반지름이며, 두 끝 사이에 일정한 압력 구배를 가하면, 속도 분포와 환형 파이프를 통한 부피 플럭스는 다음과 같습니다.

${\displaystyle {\begin{aligned}u(r)&={\frac {G}{4\mu }}\left(R_{1}^{2}-r^{2}\right)+{\frac {G}{4\mu }}\left(R_{2}^{2}-R_{1}^{2}\right){\frac {\ln r/R_{1}}{\ln R_{2}/R_{1}}},\\[6pt]Q&={\frac {G\pi }{8\mu }}\left[R_{2}^{4}-R_{1}^{4}-{\frac {\left(R_{2}^{2}-R_{1}^{2}\right)^{2}}{\ln R_{2}/R_{1}}}\right].\end{align}}}$

R = R, R = 0 이 되면 원래 문제가 복구됩니다.

압력 구배가 진동하는 파이프 내 푸아수유 흐름

진동 압력 구배가 있는 파이프를 통한 흐름은 큰 동맥을 통한 혈류에서 응용을 찾습니다.^{[13][14][15][16]} 부과된 압력 구배는 다음과 같습니다.

${\displaystyle {\frac {\partial p}{\partial x}}=-G-\alpha \cos \omega t-\beta \sin \omega t}$

여기서 G, α, β는 상수이고 ω는 주파수입니다. 속도장은 다음과 같이 주어집니다.

${\displaystyle u(r,t)={\frac {G}{4\mu }}\left(R^{2}-r^{2}\right)+[\alpha F_{2}+\beta (F_{1}-1)]{\frac {\cos \omega t}{\rho \omega }}+[\beta F_{2}-\alpha (F_{1}-1)]{\frac {\sin \omega t}{\rho \omega }}}$

어디에

${\displaystyle {\begin{aligned}F_{1}(kr)&={\frac {\mathrm {ber} (kr)\mathrm {ber} (kR)+\mathrm {bei} (kr)\mathrm {bei} (kR)}{\mathrm {ber} ^{2}(kR)+\mathrm {bei} ^{2}(kR)}},\\[6pt]F_{2}(kr)&={\frac {\mathrm {ber} (kr)\mathrm {bei} (kR)-\mathrm {bei} (kr)\mathrm {ber} (kR)}{\mathrm {ber} ^{2}(kR)+\mathrm {bei} ^{2}(kR)}},\end{aligned}}}$

여기서 ber와 bei는 켈빈 함수이고 k = ρω/μ입니다.

플레인 포이슈이류

Poiseuille flow는 무한히 긴 평행한 두 판 사이에서 생성되는 흐름으로, 일정한 압력 구배 G = -dp/ dx가 흐름 방향으로 적용되는 거리 h만큼 떨어져 있습니다. 흐름은 무한한 길이 때문에 본질적으로 단방향입니다. 나비에– 스톡 방정식은 다음으로 줄어듭니다.

${\displaystyle {\frac {\mathrm {d} ^{2}u}{\mathrm {d} y^{2}}}=-{\frac {G}{\mu }}}$

양쪽 벽에 slip이 없는 상태로

${\displaystyle u(0)=0,\quad u(h)=0}$

따라서, 속도 분포와 단위 길이당 체적 유량은

${\displaystyle u(y)={\frac {G}{2\mu }}y(h-y),\quad Q={\frac {Gh^{3}}{12\mu }}.}$

일부 비원형 단면을 통과하는 푸아수이유.

Joseph Boussinesq는 1868년에 정삼각형 단면의 직사각형 채널과 튜브 및 타원형 단면에 대한 속도 프로파일과 부피 유량을 도출했습니다.^[17] 조셉 프라우드먼은 1914년에 이등변 삼각형에 대해서도 같은 것을 유도했습니다.^[18] G = -dp/ dx을 운동과 평행한 방향으로 작용하는 일정한 압력 구배라고 가정합니다.

높이 0 ≤ y ≤ h 및 폭 0 ≤ z ≤ l인 직사각형 채널에서의 속도 및 체적 유량

${\displaystyle {\begin{aligned}u(y,z)&={\frac {G}{2\mu }}y(h-y)-{\frac {4Gh^{2}}{\mu \pi ^{3}}}\sum _{n=1}^{\infty }{\frac {1}{(2n-1)^{3}}}{\frac {\sinh(\beta _{n}z)+\sinh[\beta _{n}(l-z)]}{\sinh(\beta _{n}l)}}\sin(\beta _{n}y),\quad \beta _{n}={\frac {(2n-1)\pi }{h}},\\[6pt]Q&={\frac {Gh^{3}l}{12\mu }}-{\frac {16Gh^{4}}{\pi ^{5}\mu }}\sum _{n=1}^{\infty }{\frac {1}{(2n-1)^{5}}}{\frac {\cosh(\beta _{n}l)-1}{\sinh(\beta _{n}l)}}.\end{align}}}$

변의 길이가 2h/√3인 정삼각형 단면을 가지는 관의 속도 및 체적 유량은

${\displaystyle {\begin{aligned}u(y,z)&=-{\frac {G}{4\mu h}}(y-h)\left(y^{2}-3z^{2}\right),\\[6pt]Q&={\frac {Gh^{4}}{60{\sqrt {3}}\mu }}.\end{align}}}$

직각 이등변 삼각형 y = π, y ± z = 0에서의 속도 및 체적 유량은

${\displaystyle {\begin{aligned}u(y,z)&={\frac {G}{2\mu }}(y+z)(\pi -y)-{\frac {G}{\pi \mu }}\sum _{n=1}^{\infty }{\frac {1}{\beta _{n}^{3}\sinh(2\pi \beta _{n})}}\left\{\sinh[\beta _{n}(2\pi -y+z)]\sin[\beta _{n}(y+z)]-\sinh[\beta _{n}(y+z)]\sin[\beta _{n}(y-z)]\right\},\quad \beta _{n}=n+{\tfrac {1}{2}},\\[6pt]Q&={\frac {G\pi ^{4}}{12\mu }}-{\frac {G}{2\pi \mu }}\sum _{n=1}^{\infty }{\frac {1}{\beta _{n}^{5}}}\left[\coth(2\pi \beta _{n})+\csc(2\pi \beta _{n})\right].\end{align}}}$

반축 a와 b를 갖는 타원형 단면의 관에 대한 속도 분포는 다음과^[11] 같습니다.

${\displaystyle {\begin{aligned}u(y,z)&={\frac {G}{2\mu \left({\frac {1}{a^{2}}}+{\frac {1}{b^{2}}}\right)}}\left(1-{\frac {y^{2}}{a^{2}}}-{\frac {z^{2}}{b^{2}}}\right),\\[6pt]Q&={\frac {\pi Ga^{3}b^{3}}{4\mu \left(a^{2}+b^{2}\right)}}.\end{align}}}$

여기서 원형관에 대한 a = b, poiseuil 유동이 회복되고 a → ∞이 회복되면 평면 Poiseuil 유동이 회복됩니다. Ratip Berker에 의해 검토된 바와 같이 달팽이 모양의 섹션, 반원을 따르는 노치 원 모양의 섹션, 호모포칼 타원 사이의 환형 섹션, 비구심 원 사이의 환형 섹션과 같은 단면을 갖는 보다 명확한 솔루션도 이용할 수 있습니다.^[19][20]

임의의 단면을 통과하는 푸아슈유 흐름

임의의 단면 u(y,z)를 통과하는 흐름은 벽면에서 u = 0이라는 조건을 만족합니다. 지배 방정식은 다음과^[21] 같이 감소합니다.

${\displaystyle {\frac {\partial ^{2}u}{\partial y^{2}}+{\frac {\partial ^{2}u}{\partial z^{2}}=-{\frac {G}{\mu}}}$

새로운 종속변수를 도입하면

${\displaystyle U=u+{\frac {G}{4\mu }}\left(y^{2}+z^{2}\right),}$

그렇다면 문제가 라플라스 방정식을 적분하는 것으로 줄어든다는 것을 쉽게 알 수 있습니다.

${\displaystyle {\frac {\partial ^{2}U}{\partial y^{2}}}+{\frac {\partial ^{2}U}{\partial z^{2}}}=0}$

조건을 만족시키는

${\displaystyle U={\frac {G}{4\mu }}\left(y^{2}+z^{2}\right)}$

벽에는.

등온기체에 대한 포이슈유 방정식

튜브 내 압축성 유체의 경우 체적 유량 Q(x)와 축방향 속도는 튜브를 따라 일정하지 않지만 질량 유량은 튜브 길이를 따라 일정합니다. 체적 유량은 일반적으로 출구 압력으로 표시됩니다. 유체가 압축되거나 팽창되면 작업이 완료되고 유체가 가열되거나 냉각됩니다. 이는 유량이 유체와의 열 전달 및 유체로부터의 열 전달에 따라 달라진다는 것을 의미합니다. 유체의 온도가 주변과 평형을 이루는 등온의 경우 이상적인 기체의 경우 압력 강하에 대한 근사적인 관계를 도출할 수 있습니다.^[22] 이상적인 가스 상태 방정식을 사용하여 일정한 온도 프로세스(즉, $p{\displaystyle }$/$$ρ {\$displaystyle$p/\rho }는 일정함)와 질량 유량의 보존($즉$ m ˙ = ρ $Q${\displaystyle {\m}}=\rho Q}는 일정함)을 통해 Qp = Qp = Qp 관계를 얻을 수 있습니다. 배관의 짧은 구간에 걸쳐 배관을 흐르는 가스가 압축성이 없는 것으로 추정하여 포이슈유 법칙을 국부적으로 사용할 수 있도록 하고,

${\displaystyle -{\frac {\mathrm {d} p}{\mathrm {d} x}}={\frac {8\mu Q}{\pi R^{4}}}={\frac {8\mu Q_{2}p_{2}}{\pi pR^{4}}}\quad \Rightarrow \quad -p{\frac {\mathrm {d} p}{\mathrm {d} x}}={\frac {8\mu Q_{2}p_{2}}{\pi R^{4}}}.}$

여기서 우리는 국소 압력 구배가 압축성 효과를 갖기에는 너무 크지 않다고 가정했습니다. 국소적으로는 밀도 변화로 인한 압력 변화의 영향을 무시했지만, 장거리에서는 이러한 영향이 고려됩니다. μ는 압력에 독립적이므로 위 식을 길이 L에 적분하여 다음을 얻을 수 있습니다.

${\displaystyle p_{1}^{2}-p_{2}^{2}={\frac {16\mu LQ_{2}p_{2}}{\pi R^{4}}}.}$

따라서 파이프 출구의 체적 유량은 다음과 같습니다.

${\displaystyle Q_{2}={\frac {\pi R^{4}}{16\mu L}}\left({\frac {p_{1}^{2}-p_{2}^{2}}{p_{2}}}\right)={\frac {\pi R^{4}\left(p_{1}-p_{2}\right)}{8\mu L}}{\frac {\left(p_{1}+p_{2}\right)}{2p_{2}}}.}$

이 식은 출구 압력에 대한 평균 압력을 표현하는 추가 보정 계수 p₁ + p₂/2p를₂ 갖는 Poiseuille의 법칙으로 볼 수 있습니다.

전기 회로 비유

이 섹션에서는 출처를 인용하지 않습니다. 신뢰할 수 있는 출처에 인용을 추가하여 이 섹션을 개선하는 데 도움을 주세요. 출처가 없는 재료는 문제가 발생하여 제거될 수 있습니다. (2016년 9월) (본 템플릿 메시지의 제거 방법 및 시기에 대해 알아보기)

전기는 원래 일종의 유체로 이해되었습니다. 이 수압적 비유는 여전히 회로를 이해하는 데 개념적으로 유용합니다. 이 비유는 또한 회로 도구를 사용하여 유체-기계 네트워크의 주파수 응답을 연구하는 데 사용되며, 이 경우 유체 네트워크를 유압 회로라고 합니다. Poiseuille의 법칙은 전기 회로에 대한 옴의 법칙인 V = IR에 해당합니다. 유체에 작용하는 알짜 힘은 S = πr = S δr = πr δr δr와 같으므로 푸아수유 법칙에서 다음과 같습니다.

${\displaystyle \mathrm{}}$ F = $8μL$ Qr2 {\displaystyle \Delt${\displaystyle \mathrm{a}}$ F = {\frac {8\mu LQ}{r^{2}}}.

전기 회로의 경우 자유 전하를 띤 입자의 농도(m⁻³)라고 하고 q*를 각 입자의 전하(쿨롬 단위)라고 합니다. (전자의 경우 q* = e = 1.6×10 C.) 그러면 nQ는 부피 Q에 있는 입자의 수이고 nQq*는 그들의 총 전하입니다. 이것은 단위 시간당 단면을 흐르는 전하, 즉 전류 I입니다. 따라서 저는 = nQq*입니다. 결과적으로, Q = I/nq*, 그리고

${\displaystyle \Delta F={\frac {8\mu LI}{nr^{2}q^{*}}}$

그러나 δF = Eq, 여기서 q는 튜브 부피의 총 전하량입니다. 튜브의 부피는 πrL과 같으므로 이 부피에 있는 하전 입자의 수는 n πrL과 같으며 총 전하량은 q = n πrLq*입니다. 전압 V = EL 이므로 다음과 같습니다.

${\displaystyle V={\frac {8\mu LI}{n^{2}\pir^{4}\left(q^{*}\right)^{2}}.$

이것이 바로 옴의 법칙이며, 여기서 저항 R = V/I는 공식으로 설명됩니다.

${\displaystyle R}$ = ${\displaystyle 8}$ ${\displaystyle \frac{\mu }{}}$L ${\displaystyle n}$ 2 π r 4${\displaystyle }$(q ∗) 2 {\displaystyl${\displaystyle e}$ R = {\frac {8\mul L} {n^{2}\pir^{4}\left(q^{*}\right)^{2}}.

따라서 저항 R은 저항기의 길이 L에 비례하며 참입니다. 그러나 저항 R은 반경 r의 네 번째 파워에 반비례하며, 즉 저항 R은 저항기의 단면적 S = πr의 두 번째 파워에 반비례하며, 이는 전기식과 다릅니다. 저항에 대한 전기적 관계는

${\displaystyle R={\frac {\rholL}{S}},}$

여기서 ρ는 저항률입니다. 즉, 저항 R은 저항기의 단면적 S에 반비례합니다. Poiseuille의 법칙이 저항 R에 대한 다른 공식으로 이어지는 이유는 유체 흐름과 전류의 차이입니다. 전자 가스는 불투명하기 때문에 속도는 전도체 벽까지의 거리에 의존하지 않습니다. 저항은 흐르는 전자와 전도체 원자 사이의 상호작용 때문입니다. 따라서 포이슈유의 법칙과 수압적 비유는 전기에 적용할 때 일정한 한계 내에서만 유용합니다. 옴의 법칙과 포이슈유의 법칙은 모두 수송 현상을 설명합니다.

의료 애플리케이션 – 정맥내 접근 및 수액 전달

이 섹션에서는 출처를 인용하지 않습니다. 신뢰할 수 있는 출처에 인용을 추가하여 이 섹션을 개선하는 데 도움을 주세요. 출처가 없는 재료는 문제가 발생하여 제거될 수 있습니다. (2016년 9월) (본 템플릿 메시지의 제거 방법 및 시기에 대해 알아보기)

Hagen-Poiseuille 방정식은 다양한 크기의 말초 캐뉼라 및 중앙 캐뉼라를 사용하여 달성할 수 있는 정맥(IV) 유체의 혈관 저항 및 유량을 결정하는 데 유용합니다. 이 방정식은 유량이 네 번째 동력에 대한 반지름에 비례한다는 것을 의미하며, 캐뉼라의 내경이 조금만 증가하면 IV 유체의 유량이 크게 증가한다는 것을 의미합니다. IV 캐뉼라의 반경은 일반적으로 반경에 반비례하는^{[dubious – discuss]} "게이지"로 측정됩니다. 주변 IV 캐뉼라는 일반적으로 (큰 것부터 작은 것까지) 14G, 16G, 18G, 20G, 22G, 26G로 제공됩니다. 예를 들어, 14G 캐뉼라의 흐름은 일반적으로 16G의 약 2배^{[citation needed]}, 20G의 10배입니다^{[citation needed]}. 또한 흐름은 길이에 반비례한다고 명시하고 있는데, 이는 긴 라인이 더 낮은 유량을 가지고 있다는 것을 의미합니다. 응급 상황에서 많은 임상의들이 길고 좁은 카테터에 비해 더 짧고 큰 카테터를 선호하기 때문에 이 점을 기억하는 것이 중요합니다. 임상적 중요성은 덜하지만 유체 백을 가압하거나 백을 쥐어짜거나 백을 더 높게 걸거나(캐뉼라 수준에 비해), 압력의 증가된 변화(∆p)를 사용하여 유속을 빠르게 할 수 있습니다. 점성 유체는 (예를 들어, 수혈 시) 더 느리게 흐르게 된다는 것을 이해하는 것도 유용합니다.

참고 항목

• 쿠에트 흐름
• 달시의 법칙
• 맥박
• 파도.
• 유압회로

인용참고문헌

참고문헌

• Sutera, S. P.; Skalak, R. (1993). "The history of Poiseuille's law". Annual Review of Fluid Mechanics. 25: 1–19. Bibcode:1993AnRFM..25....1S. doi:10.1146/annurev.fl.25.010193.000245..
• Pfitzner, J (1976). "Poiseuille and his law". Anaesthesia. Vol. 31, no. 2 (published Mar 1976). pp. 273–5. doi:10.1111/j.1365-2044.1976.tb11804.x. PMID 779509..
• Bennett, C. O.; Myers, J. E. (1962). Momentum, Heat, and Mass Transfer. McGraw-Hill..

외부 링크

• 비뉴턴 유체에 대한 멱법칙 포이슈유의 법칙
• 약간 테이퍼진 관 속의 포이슈유 법칙
• 하겐-포이슈유 방정식 계산기