힐 클라이밍

이 글은 검증을 위해 추가 인용문이 필요합니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선하는 데 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.출처 : '힐 클라이밍'– 뉴스 · 신문 · 서적 · 학자 · JSTOR (2017년 4월) (이 템플릿 메시지 삭제 방법 및 삭제 시기 확인)

그래프와 트리 검색 알고리즘
α–β 가지치기 역추적 빔 검색 베스트 퍼스트 검색 브랜치&바운드 폭 우선 검색(BFS) 대영박물관 깊이 우선 검색(DFS) 힐 클라이밍 반복 심화 DFS(IDDFS) 사전 편찬 BFS
최단 경로
A* B* 벨먼-포드 양방향 검색 D* 다이크스트라의 플로이드 워셜 프린지 검색 반복심화(IDA*) 존슨즈 점프 포인트 검색 크루스칼의 라이프 사이클 계획 A* (LPA*) 경로 검색 SMA*
리스트
그래프 알고리즘 검색 알고리즘 그래프 알고리즘 목록
관련 토픽
동적 프로그래밍 그래프 색칠 그래프 트래버설 최소 스패닝 트리 게임 검색 스레드 바이너리 트리 트리 트래버설
v t

수치 분석에서, 언덕 오르기는 로컬 검색 패밀리에 속하는 수학적 최적화 기술입니다.이것은 문제에 대한 임의의 해결책에서 시작하여 해결책에 대한 증분 변경을 통해 더 나은 해결책을 찾는 반복 알고리즘입니다.변경으로 인해 더 나은 솔루션이 생성되면 새로운 솔루션에 대한 추가 변경이 이루어지고 더 이상 개선 사항이 발견되지 않을 때까지 계속 변경됩니다.

예를 들어, 출장 세일즈맨 문제에 언덕 오르기를 적용할 수 있습니다.모든 도시를 방문하는 초기 솔루션을 쉽게 찾을 수 있지만 최적 솔루션에 비해 매우 빈약할 수 있습니다.알고리즘은 이러한 솔루션에서 시작하여 두 도시를 방문하는 순서를 바꾸는 등 이를 약간 개선합니다.결국 훨씬 더 짧은 루트를 얻을 수 있을 것이다.

힐 클라이밍은 볼록한 문제에 대한 최적의 해결책을 찾습니다.다른 문제에 대해서는 로컬 옵티마(인접 구성에 의해 개선될 수 없는 솔루션)만을 찾습니다.이러한 솔루션들은 가능한 모든 솔루션(서치 공간) 중에서 반드시 최선의 솔루션(글로벌 옵티마)은 아닙니다.언덕을 오르면서 볼록한 문제를 해결하는 알고리즘의 예로는 선형 프로그래밍과 이진 ^{[1]: 253} 검색을 위한 심플렉스 알고리즘이 있습니다.로컬 최적화에 고착되지 않도록 하려면 재시작(즉, 반복 로컬 검색) 또는 반복(반복 로컬 검색과 같은)에 기반한 보다 복잡한 체계 또는 메모리(반응적 검색 최적화 및 tabu 검색과 같은) 또는 메모리 없는 확률적 수정(시뮬레이션 어닐링과 같은)을 사용할 수 있다.

알고리즘은 비교적 단순하기 때문에 최적화 알고리즘 중 가장 인기 있는 선택지가 됩니다.이것은 인공지능에서 출발 노드에서 목표 상태에 도달하기 위해 널리 사용됩니다.관련 알고리즘에서는 다음 노드와 시작 노드에 대해 서로 다른 선택사항이 사용됩니다.시뮬레이션 어닐링이나 타부 검색과 같은 고급 알고리즘이 더 나은 결과를 제공할 수 있지만 상황에 따라서는 언덕 오르기가 똑같이 작동합니다.일반적으로 소수의 증분이 적절한 솔루션(최적의 솔루션 또는 근사치)에 수렴되는 한 실시간 시스템 등 검색 수행에 사용할 수 있는 시간이 제한되어 있는 경우 언덕 오르기는 다른 알고리즘보다 더 나은 결과를 얻을 수 있습니다.다른 극단적으로 버블 정렬은 언덕 오르기 알고리즘으로 볼 수 있지만(인접 요소 교환마다 무질서 요소 쌍의 수가 감소), 필요한 교환 수가 2차적으로 증가하므로 이 접근방식은 약간의 N에도 효과적이지 않다.

힐 클라이밍은 언제든지 사용할 수 있는 알고리즘입니다.언제든지 종료되기 전에 중단되어도 유효한 솔루션을 반환할 수 있습니다.

수학적 설명

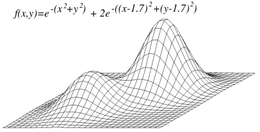
힐 클라이밍은 목표 $함수{\displaystyle }$ f$($${\displaystyle x\mathbf{}}$)(\$displaystyle$ f$(\mathbf$${x$$})$를 최대화(또는 최소화)하려고 합니다.$여기$서$$x {\$displaystyle \mathbf${x$}$는 연속 및/또는 이산 값의 벡터입니다.각 반복에서 힐 클라이밍은 x$(\$의 단일 요소를 조정하고 ${\displaystyle 변경}$으로${\displaystyle }$f$(\displaystyle$ f$(\mathbf$ ${$$x$의 값이 개선되는지 여부를 판단합니다.(이는$$x$(\displaystyle$ \$mathbf$${$x$})$의 모든 값을 조정하는 경사 하강법과는 다릅니다).힐의 기울기에 따라 반복한다.)힐 클라이밍에서는 f$x)\displaystyle$ f$(\mathbf {x})$를 $개선$하는 변경이 받아들여지고 f$)\displaystyle$ f$(\mathbf {x$의 값을 $개선$하는 변경이 발견되지 않을 때까지 프로세스가 계속됩니다.$그러면{\displaystyle \mathbf{}}$ x$(\$가 "로컬 최적"이라고 합니다.

이산 벡터 공간에서 x$(\$에 대해 $가능$한 각 값은 그래프에서 정점으로 시각화할 수 있습니다.힐 클라이밍은 정점에서 정점으로 그래프를 따르며 로컬 최대값(또는 로컬 최소값) ${\displaystyle x_{}}$m$({displaystyle$ x_{$m})$에 도달할 때까지 항상 f$x)$ {$displaystyle$ f$(\mathbf {x$의 $값$을 로컬로 증가(또는 감소)합니다.

변종

단순 언덕 오르막에서는 첫 번째 근접 노드가 선택되지만, 가장 가파른 오르막 오르막에서는 모든 후속 노드가 비교되고 솔루션에 가장 가까운 노드가 선택됩니다.두 양식 모두 가까운 노드가 없으면 실패합니다. 검색 공간에 솔루션이 아닌 로컬 최대값이 있는 경우 발생할 수 있습니다.가장 가파른 오르막길은 현재 경로의 가능한 모든 연장을 1개 대신 시도하는 베스트 퍼스트 서치(best first search는 best-first search와 유사합니다.

확률적 언덕등반은 어떻게 움직일지를 결정하기 전에 모든 이웃을 검사하는 것은 아니다.대신 네이버를 랜덤으로 선택하고 (그 네이버의 개선 정도에 따라) 해당 네이버로 이동할지 또는 다른 네이버를 조사할지를 결정합니다.

좌표 강하에서는 각 반복의 현재 지점에서 하나의 좌표 방향을 따라 선을 검색합니다.좌표 강하의 일부 버전은 반복할 때마다 다른 좌표 방향을 무작위로 선택합니다.

랜덤 재시작 힐 클라이밍은 힐 클라이밍 알고리즘 위에 구축된 메타 알고리즘입니다.그것은 또한 샷건 힐 클라이밍으로도 알려져 있다.임의의 초기 $조건{\displaystyle {}_{}}$ ${\displaystyle {x\mathrm{}}_{}}$ 0$(\$을 사용하여 매번 반복적으로 언덕을 올라갑니다.$최적$의 ${\displaystyle x_{}}$ m$({$${m$})이$$ 유지됩니다.새로운 힐 클라이밍으로 인해 저장된 상태보다 더 $나은{\displaystyle {}_{}}$ ${\displaystyle x_{}}$ m$({$m$$})이 생성되면 저장된 상태를 대체합니다.

랜덤 리스타트 힐 클라이밍은 많은 경우 놀라울 정도로 효과적인 알고리즘입니다.CPU의 ^{[original research?]}시간을 들여 공간을 탐색하는 것이 초기 상태부터 신중하게 최적화하는 것보다 더 나은 경우가 많습니다.

문제

국소 최대값

언덕을 오르는 것이 반드시 세계적인 최고치를 찾는 것은 아니지만, 대신 국지적인 최고치에 모일 수 있다.휴리스틱이 볼록한 경우에는 이 문제가 발생하지 않습니다.그러나 많은 기능이 볼록한 언덕이 아니기 때문에 종종 전지구적 최대치에 도달하지 못할 수 있다.다른 지역 검색 알고리즘은 확률적 언덕 오르기, 랜덤 워크 및 시뮬레이션 어닐링과 같은 이 문제를 극복하기 위해 노력합니다.

능선과 골목

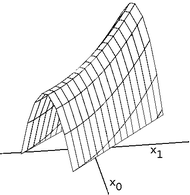
연속된 공간에서 최적화하는 언덕 등반가들에게 능선은 어려운 문제입니다.힐 클라이머는 한 번에 벡터의 한 요소만 조정하므로 각 스텝은 축 정렬 방향으로 이동합니다.대상 함수가 비축 정렬 방향으로 상승하는 좁은 능선을 작성하는 경우(또는 비축 정렬 방향으로 하강하는 좁은 골목길을 최소화하는 경우), 힐 클라이머는 지그재깅을 통해 능선을 상승(또는 골목 아래로 하강)할 수 있습니다.능선(또는 골목)의 측면이 매우 가파르면, 언덕 등반가들은 더 나은 위치를 향해 지그재그로 움직이기 때문에 아주 작은 발걸음을 내딛어야 할 수도 있다.따라서 산등성이를 오르거나 골목길을 내려가기까지 시간이 너무 오래 걸릴 수 있다.

반면 경사 하강법은 능선이나 골목이 오르내리는 방향으로 이동할 수 있다.따라서 목표 함수가 미분 가능한 경우 경사 강하 또는 켤레 경사 방법이 언덕 등반보다 일반적으로 선호된다.그러나 힐 클라이머는 표적 기능이 구별될 필요가 없다는 장점이 있으므로 표적 기능이 복잡할 경우 힐 클라이머가 선호될 수 있다.

고원

언덕을 오를 때 가끔 발생하는 또 다른 문제는 고원이다.서치공간이 평탄하거나 그 값을 나타내기 위해 기계에 의해 사용되는 정밀도로 인해 목표함수에 의해 반환된 값과 인근 영역에 대해 반환된 값을 구별할 수 없을 정도로 평탄할 때 고원이 발생한다.이러한 경우, 언덕을 오르는 사람은 어느 방향으로 가야 할지 결정하지 못하고 개선으로 이어지지 않는 방향으로 헤매게 될 수 있다.

유사코드 알고리즘 이산 공간 힐 상승은 currentNode : = startNode 루프 do L : = NAVERS ( currentNode ) nextEVal ( x ) > nexteval , nexteval , nexteval , nexteval , node : = NEVAL ( nexteval ) （ nexteval ; nexteval ; nexteval ; nexteval ; nexteval ; next Eval ; node ） ≤ eval next next next next next next next next next next next next next next next next next next next next next next next next next next// 더 나은 네이버가 없으므로 현재 노드를 반환합니다. currentNode currentNode : = nextNode

알고리즘 연속 공간 언덕 오르기는 currentPoint := initialPoint // 0-규모 벡터는 공통 스텝사이즈 // 모든 1의 벡터는 공통 가속도 := someAcceleration // 1.2와 같은 값은 공통 후보 [0] : = - = - 1 / acceleration 후보 [ 2 ]입니다.1/가속 후보[3] := 가속 bestScore := EVAL(currentPoint) 루프 스코어 := beforeScore := beforeCurrentPoint [i] beforePoint := beforecurrentPoint [i] bestStep := 0 ~ 3 do j에 대해 bestScore // 4개 후보 위치 각각 시도:= STEP:=Ize[나는]× candidate[j]currentPoint[나는]:)beforePoint+단계 점수:)EVAL(currentPoint)만약 점수>bestScore 다음 bestScore:= 점수 bestStep:= 단계 bestStep은 0다음 currentPoint[나는]:)beforePoint stepSize[나는]. :)stepSize[i] / acceleration else currentPoint[i] : = beforeStepSize [i] : = bestStep // 가속(bestScore - beforeScore) < 엡실론인 경우 currentPoint를 반환합니다.

대조 유전 알고리즘, 무작위 최적화.

「 」를 참조해 주세요.

• 경사 강하강
• 탐욕 알고리즘
• 톤네먼트
• 평균 이동
• A* 검색 알고리즘

레퍼런스

• Russell, Stuart J.; Norvig, Peter (2003), Artificial Intelligence: A Modern Approach (2nd ed.), Upper Saddle River, New Jersey: Prentice Hall, pp. 111–114, ISBN 0-13-790395-2

추가 정보

• Lasry, George (2018). A Methodology for the Cryptanalysis of Classical Ciphers with Search Metaheuristics (PDF). Kassel University Press. ISBN 978-3-7376-0459-8.

외부 링크

• Wikibooks에서의 힐 클라이밍