램버트 W 함수

수학에서, 오메가 함수 또는 곱 로그라고도 불리는 램버트 W 함수는 다치 함수이다. 즉, 함수 f(w^w) = we의 역관계의 분기이다. 여기서^w w는 복소수이고 e는 지수 함수이다.

각 정수 k에 대해 W(z)로_k 나타나는 분기가 하나 있는데, 이는 하나의 복잡한 인수의 복소수 함수이다.W는₀ 주요 분기로 알려져 있습니다.이러한 함수에는 다음과 같은 특성이 있습니다. z와 w가 복소수이면

${\displaystyle we^{w}=z}$

만약의 경우에 한하여 유지되다

${\displaystyle w=W_{k}(z)\\{text{일부 정수}}k.}$

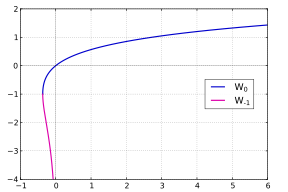
실수만을 취급하는 경우, 2개의₋₁ 분기₀ W와 W로 충분합니다.실수 x와 y의 방정식은 다음과 같습니다.

${\displaystyle ye^{y}=x}$

경우에만 x≥−.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{y에 해결될 수 있습니다.Border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}1/e;if)과 두 값이 y)W0())와 y0≥ 만약 −1/e ≤)<>우리는))y W0())W−1())이 가지고 0.

램버트 W 관계는 기본 함수로 ^[1]표현할 수 없다.예를 들어 트리 열거와 같은 조합학에서 유용합니다.이는 지수를 포함한 다양한 방정식(예를 들어 플랑크, 보스-아인슈타인, 페르미-디락 분포의 최대값)을 푸는 데 사용될 수 있으며, yθ(t) = y(t - 1)와 같은 지연 미분 방정식의 해에서도 발생한다.생화학, 특히 효소 동역학에서, Michaelis-Menten 역학의 시간 과정 동역학 분석을 위한 열린 형태의 용액은 Lambert W 함수의 관점에서 설명된다.

복소 평면에서 도메인 색상으로 표시된 Lambert W 함수의 주요 가지.-1/e에서 끝나는 음의 실제 축을 따라 가지를 잘라냅니다.

용어.

램버트 W 함수는 요한 하인리히 램버트(Johann Heinrich Lambert)의 이름을 따왔다.주요 분기₀ W는 디지털 수학 함수 라이브러리에서 Wp로 표시되고 분기₋₁ W는 Wm으로 표시됩니다.

여기서 선택한 표기법 규칙₋₁(W와 W 포함₀)은 콜리스, 곤넷, 헤어, 제프리 및 ^[2]크누스에 의해 램버트 W 함수에 대한 표준 참조를 따른다.

"제품 로그"라는 이름은 다음과 같이 이해할 수 있습니다.f(w) = e의^w 역함수를 로그라고 부르기 때문에 곱의^w 역함수를 곱 로그라고 부르는 것이 타당하다. (기술적 주: 이것은 다치이므로 실제로는 함수가 아니므로 W는 역함수가 아닌 역함수로 설명된다.)이것은 W(1)와 같은₀ 오메가 상수와 관련이 있습니다.

역사

램버트는 1758년에 관련된 램버트의 초월 ^[3]방정식을 처음으로 고려했고, 이것은 1783년에^[4] 레온하르트 오일러에 의해 우리의 특별한^w 경우를 논한 기사로 이어졌다.

램버트가 고려한 함수는

${\displaystyle x=x^{m}+q}$

오일러는 이 방정식을 변형시켰다.

${\displaystyle x^{a}-x^{b}=(a-b)cx^{a+b}}$

두 저자 모두 방정식에 대한 급수 해답을 도출했다.

일단 오일러가 이 방정식을 풀면, 그는 a = b인 경우를 고려했다.한계를 가지고 그는 방정식을 도출했다.

$(\displaystyle\ln x=cx^{a}).}$

그런 다음 a = 1을 대입하고 결과 방정식에 대한 수렴 급수 해를 구했는데, x는 c로 표현했습니다.

x 및 일부 조작에 관한 도함수를 취한 후 램버트 함수의 표준 형태를 구한다.

1993년, 램버트 W 함수는 물리학의 근본적인 문제인 등전하에^[5] 대해 양자역학적 이중 웰 디락 델타 함수 모델에 정확한 해답을 제공하는 것으로 보고되었다.이에 고무된 롭 콜리스와 메이플 컴퓨터 대수학 시스템의 개발자들은 "램버트 W 함수는 많은 분야에서 널리 사용되어 왔지만, 표기법이 다르고 표준 이름이 없기 때문에 함수에 대한 인식이 그렇게 ^[2][6]높지 않았다는 것을 깨달았다."

이 함수가 발견된 또 다른 예는 Michaelis-Menten 속도론이다.^[7]

램버트 W 함수는 초등(리우빌리안) 함수의 관점에서 표현될 수 없다고 널리 믿어졌지만,^[8] 2008년에야 처음으로 발표된 증거가 나타났다.

기본 속성, 분기 및 범위

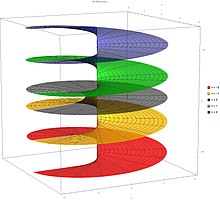
정수 k(또는 주요) 분기에 대해 W(z)로 표시되는_k W 함수의 분기는 셀 수 없을 정도로 많습니다. W₀₀(z)는 모든 복소수 z에 대해 정의되며, k_k 0 0인 W(z)는 모든 비제로 z에 대해 정의됩니다.모든 k 0 0에 대해 W(0) = 0 및 limz→0_k W(z) = -126이 있습니다₀.

주가지에 대한 분기점은 z = -1/e이며, 음의 실제 축을 따라 -420까지 확장되는 분기 절단이 있습니다.이 가지 절단부는 주요 가지와₁ 두 가지 가지 가지₋₁ W와 W를 분리합니다.k 0 0인 모든 가지_k W에는 z = 0인 가지점과 음의 실축 전체를 따라 절단된 가지가 있다.

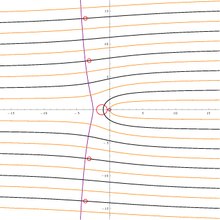
함수_k W(z), k z Z는 모두 주입식이며 범위는 분리된다.전체 다치 함수 W의 범위는 복소 평면이다.실제 축의 이미지는 실제 축과 Hippias의 4분율, 파라메트릭 곡선 w = -t cot t + it의 결합입니다.

역

위의 범위 그림은 또한 단순한 $역관계{\displaystyle }$ W${\displaystyle (n,}$ ${\displaystyle z}$ ${\displaystyle {}^{}{z}^{}}$) $=$ {$displaystyle$ W$(n,ze^{z$})=$z}$가 참인 복소 평면에서 영역을 나타낸다.f^z = ze는 z ${\displaystyle =W}$ (${\displaystyle }$n ,${\displaystyle f}$ ) ${\displaystyle =W}$ (${\displaystyle n}$ , ${\displaystyle z}$ ${\displaystyle e^{}}$z$$) { $displaystyle$ z $= W$ ($n$ , f ) $= W$ ( $n$, $ze^{z}}$} 이 $존재함$을 의미합니다. 여기서 n은 z의 값에 따라 달라집니다.ze가 W${\displaystyle (n,}$ z ${\displaystyle e^{}}$ z$)$의 $분기{\displaystyle }$ 컷(\$displaystyle$ W$(n,ze^{z$에 있을 때^z 정수 n의 값이 갑자기 변화한다. 즉, ze ${\displaystyle 0}$ 0(n ${\displaystyle =}$ 0 \$displaystyle$ n =$0)$은^z ze - -1/e이다^z.

z ${\displaystyle =x}$ + ${\displaystyle i}$y \$style$ z=x+$iy$$display$ z=$x+$iy\, 여기서 x와 y는 실재하고 e는 극좌표로 표현하면^z $다음$과 같이 표시됩니다.

$(\displaystyle\cos y+i\sin y)ze^{z}&=(x+i)e^{x}(\cos y+i\sin y)\\&=e^{x}(x\cos y-y\sin y)+ie^{x}(x\sin y+y\cos y)\\\end {aligned}}$

n${\displaystyle 0}$0 { $displaystyle$n \ $neq$ 0$$}의 경우${\displaystyle }$W (${\displaystyle n}$ , ${\displaystyle z}$ ${\displaystyle {}^{}{z}^{}}$) { $displaystyle$W ($n$ , $ze^$ { z )$$}의 브랜치 컷은 양의 실축이 아니므로 다음과 같이 됩니다.

${\displaystyle x\sin y+y\cos y=0\오른쪽 화살표 x=-y/\tan(y),}$

그리고.

$\displaystyle (x\cos y-y\sin y) e^{x}\leq 0}$

n ${\displaystyle =}$ { $displaystyle$ n =$0$} 의 $경우{\displaystyle }$${\displaystyle ,}$ ${\displaystyle W}$[ n , ${\displaystyle z^{}}$e z $]$ { $display$ W $[ n$ , $ze ^$ {$z$ } 에 $대한{\displaystyle }$ 분기 절단은 - < $z$ - 1 / \ $display$- \$leq$- 1 / e 의 실제 축입니다.그러면 부등식이 됩니다.

$\ displaystyle ( x \ cos y - y \ sin y ) e^ { x } \ leq - 1 / e }$

상기에 의해 경계된 영역 내에서는 W${\displaystyle (n^{}}$ e z){$displaystyle W$(n$,ze^{$z$\})$에 불연속적인 변화가 없으며, 이러한 $영역$은 W 기능이 단순히 반전 가능한 위치를 지정합니다. 즉, W${\displaystyle (n,}$ ${\displaystyle {}^{}}$ e${\displaystyle {}^{}{z}^{}}$) $=$z {$displaystyle$W$($$n,ze^{z$})=$z$

미적분학.

파생상품

암묵적 미분에 의해, W의 모든 분기가 미분 방정식을 만족한다는 것을 보여줄 수 있다.

${\displaystyle z(1+W){\frac {dW}{dz}=W\quad {text{for}}z\neq-{\frac {1}{e}}}.}$

(z = -1/e의 경우 W는 미분할 수 없습니다.)그 결과, W의 도함수에 대해 다음과 같은 공식을 얻을 수 있습니다.

${\displaystyle\frac {dW}{dz}=param frac {W(z)}{z(1+W(z))}}}\text{for}znot\left,-{\frac {1}{e}}\right\}.}$

항등식^W(z) e = z/W(z)를 사용하면 다음과 같은 공식을 얻을 수 있습니다.

${\displaystyle {dW}{dz}=sq {1}{z+e^{W(z)}}}\quad {text {}z\neq - {\frac {1}{e}}}.}$

원점에는

${\displaystyle W'_{0}(0)=1.}$

일체형

함수 W(x) 및 W(x)와 관련된 많은 표현식은 w= W(x), 즉 x = we를^w 사용하여 통합할 수 있습니다.

$(\displaystyle {displaystyle {narged}\int W(x), dx&=xW(x)-e^{W(x)}+C\&=x\left(W(x)-1+{\frac {1}{W(x)}}}+C).\end { aligned}}$

(마지막 방정식은 문헌에서 더 흔하지만 x = 0에서 정의되지 않습니다.)이것의 한 가지 결과(W₀(e) = 1)는 동일성이다.

$\displaystyle \int _{0}^{e}W_{0}(x),dx=e-1.}$

점근 확장

0 주위의 W의 테일러₀ 급수는 라그랑주 반전 정리를 사용하여 찾을 수 있으며 다음과 같이 주어진다.

${\displaystyle W_{0}(x)=\sum _{n=1}^{\infty}{\frac {(-n)^{n-1}}{n!}x^{n}=x-x^{2}+{\tfrac {3}{3}-{\tfrac {8}{3}x^{4}+{\tfrac {125}{24}x^{5}-\cdots.}$

비율 테스트에서 알 수 있듯이 수렴 반경은 1/e입니다.이 시리즈에 의해 정의된 함수는 간격(-θ, -1/e)을 따라 분기가 절단된 모든 복소수에서 정의된 정칙함수로 확장될 수 있습니다. 이 정칙함수는 Lambert W 함수의 주요 분기를 정의합니다.

x 값이 클 경우, W는₀ 다음에 대해 점근적이다.

$디스플레이 스타일W_{0}(x)&=L_{1}-L_{2}+{\frac {L_{1}}+{\frac {L_{2}\left(-2+L_{2}\right)}{2}L_{1}^{2}}+{\frac {L_{2}\left(6-9L_{2}+2L_{2}^{2}\right)}{6L_{1}^{3}}+{\frac {L_{2}\left(-12+36)L_{2}-22L_{2}^{2}+3L_{2}^{3}\right}{12L_{1}^{4}}+\cdots \\[5pt]&= L_{1}-L_{2}+\sum _{l=0}^{\infty}\sum _{m=1}^{\infty}{\frac {(-1)^{l}\left[{\frac {small matrix}l+1\end{small matrix}}\righty}{m!}L_{1}^{-l-m}L_{2}^{m},\end{aligned}}$

여기서₁ L = ln x, L₂ = ln x 및 []^{l + m}
_{l + 1}는 음수가 아닌 제1종 ^[2]스털링 수이다.확장의 처음 두 항만 유지하면

${\displaystyle W_{0}(x)=\ln x-\ln x+{\mathcal {o}}(1)}$

[-1/e, 0] 구간에서 정의된 다른 실분지 W는₋₁ x가 0에 근접하는 것과 같은 형태의 근사치를 가지며, 이 경우₁ L = ln xx) 및 L₂ = ln lnlnxx)^[2]이다.

정수 및 복소수 검정력

W의 정수₀ 거듭제곱은 0에서 단순 Taylor(또는 Laurent) 직렬 확장을 허용합니다.

${\displaystyle W_{0}(x)^{2}=\sum _{n=2}^{\infty}{\frac {-2\leftfcn\right)^{n-3}{(n-2)!}x^{n}=x^{2}-2x^{3}+4x^{4}-{\tfrac {25}{3}}x^{5}+18x^{6}-\cdots.}$

보다 일반적으로, r z Z에 대해, 라그랑주 반전 공식은 다음을 나타낸다.

${\displaystyle W_{0}(x)^{r}=\sum _{n=r}^{\infty}{\frac {-r\lefthcn\right)^{n-r-1}{(n-r)!}}x^{n}}$

일반적으로 로랑 계열의 순서 r입니다.마찬가지로 후자는 Taylor의 W(x) / x의₀ 거듭제곱의 형태로 쓸 수 있다.

${\displaystyle \frac {W_{0}(x})\right}=e^{-rW_{0}(x)}=\sum _{n=0}^{\infty}{\frac {r\left(n+right)^n-1}{n!}}\left440x\right)^{n}$

이 값은 임의의 r † C 및 x < 1/e에 적용됩니다.

한계와 부등식

램버트 함수에 대해 다수의 비점근 경계가 알려져 있다.

Hoorfar와 Hassani는^[9] 다음 경계가 x µ e에 대해 유지됨을 보여주었다.

${\displaystyle \ln x-\ln x+{2\ln x}\leq W_{0}(x)\leq \ln x-\ln x+{e}{e-1}{\frac {\ln x}}.}$

그들은 또한 일반적인 경계를 나타냈다.

$\displaystyle W_{0}(x)\leq \log \left({\frac {x+y}{1+\log(y)}}}\right),}$

모든 > / \ $displaystyle$ y $> 1$ / ${\displaystyle e}$\$displaystyle$ -${\displaystyle }$1 /$$e \ $displaystyle$$$x \ $geq$ -$$ / $e$with 、 $x = y$ y $）$ $for$ only for for for for for for for for for for for for for for for 。경계를 지정하면 ${\displaystyle y}$ ${\displaystyle =}$ ${\displaystyle \mathrm{x}}$+ 1(\$displaystyle y=x+$1)을$$ $취하는{\displaystyle }$ 등 다른 경계를 만들 수 있습니다.

${\displaystyle W_{0}(x)\leq \log \left({\frac {2x+1}{1+\log(x+1)}}}\right).}$

2013년에는 지점₋₁ W가 다음과 같이 제한될 수 있다는 것이 입증되었습니다^[10].

$\displaystyle - 1 - { \ sqrt { 2u } - u < W _ { - 1 } \ left ( - e^ { - u - 1 } \ right ) < - 1 - { \ sqrt { 2 u } - { } u \ quad { text { for } u > 0 .}$

아이덴티티

정의에서 몇 가지 ID는 다음과 같습니다.

$디스플레이 스타일W_{0}(xe^{x})&=x&{\text{for }x&\geq-1,\W_{-1}(xe^{x})&=x&{\leq-1}.\end { aligned}}$

f(x) = xe는^x 주입식이 아니기 때문에 역삼각함수와 마찬가지로 항상 W(f(x) = x를 유지하는 것은 아닙니다.고정 x < 0 및 x δ -1의 경우, xe^x = ye^y 방정식은 y에 두 개의 실해가 있으며, 그 중 하나는 y = x이다.i = 0 및 x < -1 및 i = -1 및 x δ(-1, 0)의 경우 y = W_i(xe^x)가 다른 해이다.

기타 아이덴티티:^[11]

$\displaystyle\begin{aligned}&W(x)e^{W(x)}=x,\quad{text}:}}\\[5pt]&e^{W(x)}=param frac {x}{W(x)}},\qquad e^{-W(x)}=param frac {W(x)}{x},\qquad e^{nW(x)}=left({\frac {x}}}{W(x}}}}}}}{{n}}}}}}}}}{{{{nfright}}}}}}}}}}}}}}}}}}}}}}}}}}\end { aligned}}$

$\displaystyle \ln W_{0}(x)=\ln x-W_{0}(x)\quad {text{for}}x>0.}$^[12]

${\displaystyle W_{0}\left(x\ln x\right)=\ln x\context {and}\context e^{W_{0}\left(x\ln x\right)=x\context{for}{\frac {1}{e}}\leq x.}$

${\displaystyle W_{-1}\left(x\ln x\right)=\ln x\display e^{W_{-1}\left(x\ln x\right)=x\display {text}0<x\leq {frac {1}{e}.}$

${\displaystyle {begin {aligned}&W(x)=\ln {frac {x}}x\geq - {\frac {1}{e}},\[5pt]&W\left({\frac {nx^{n}}}}{W\left(x\right)^{n-1}}\right)=nW(x)&{\text{}n,x>0\end{aligned}}}$

(올바른 브랜치를 선택한 경우 다른n 및 x로 확장할 수 있습니다).

${\displaystyle W(x)+W(y)=W\left(xy\left(xy\frac {1}{W(x)}}})+{\frac {1}{W(y)}}}\right)\quad {}x,y > 0.}$

정의에서 ^[13]-ln x로 치환:

$디스플레이 스타일W_{0}\left(-{\frac {ln x}{x}\오른쪽)&=-\ln x&{\text{}}0&<x\leq e,\[5pt]W_{-1}\left(-{\frac {ln x}{x}}\오른쪽)&=-\ln x&{\text{}x&>e.\end { aligned}}$

오일러의 반복 지수 h(x)의 경우:

${\displaystyle {begin{aligned}h(x)&=e^{-W(-\ln x)}{-\ln x}}\syslog {text{for }x\neq 1.\end{aligned}}}}$

특별한 값

다음은 주요 분기의 특수값입니다.

${\displaystyle W\left(-{\frac {pi }{2}}\오른쪽)=flac {i\pi }{2}.}$

${\displaystyle W\left(-{\frac {1}{e}}\right)=-1.}$

${\displaystyle W\left(2\ln 2\right)=\ln 2.}$

$\displaystyle W\left(x\ln x\right)=\ln x\{text{제공}}\x\geqslant 1/e\약 0.36788.}$

${\displaystyle W(0)=0.}$

${\displaystyle W}$ ${\displaystyle (}$ ${\displaystyle 1}$) ${\displaystyle =}$ ${\displaystyle \mathrm{\omega }}$ ${\displaystyle {{}_{}^{}}^{}}$ω -${\displaystyle {{\mathrm{}}_{\mathrm{}}^{}\frac{d}{{}^{}}}^{}}$t ( ${\displaystyle {\frac{{e^{}}^{}}{}}^{}}$t -${\displaystyle {\frac{t^{}}{}}^{}}$ ) ${\displaystyle {\frac{{}^{}}{}}^{}}$+ ${\displaystyle {\frac{{\pi \mathrm{}}^{}}{}}^{}}$2 )${\displaystyle {}^{}}$-${\displaystyle {}^{}}$1 - ${\displaystyle 10}$0.${\displaystyle 56714329}$ $...$ ( \ $display style$W (1) = \ $Omega$=$left$( \ $int$ _ { - \ $infty }^{$ \$frac$ { $t$- $t$} ($lefty$ )

${\displaystyle W(1)=e^{-W(1)=\ln \leftflac {1}{W(1)}}\right)=-\ln W(1).}$

${\displaystyle W(e)=1.}$

$\displaystyle W\left(e^{1+e}\right)=e.}$

$(\displaystyle W(-1)\약 -0.31813+1.33723i).}$

표현

Lambert 함수의 주요 분기는 ^[14]포아송으로 인해 적절한 적분으로 나타낼 수 있습니다.

${\displaystyle - {\frac {\pi }{\pi }W(-x)=\int _{0}^{\pi }{\frac {3}{\right}-xe^{\cos t}\sin \tfrac {5}-t}-cosin {x}t}tcos {1-cos}{x}{2}}$

넓은 도메인 -1/e "x "e"에서 상당히 간단한 표현은 Mez"^[15]에 의해 발견되었습니다.

${\displaystyle W(x)=pi frac {1}{\pi }}\operatorname {Re}\int _{0}^{\pi }\ln \left frac {e^{it}-xe^{-it}}{e^{-it}}-xe^{it}}\right},d}.$

주요 분과의 또 다른 표현은 같은^[16] 저자에 의해 발견되었으며, 이전에 칼루긴-제프리-콜리스에 ^[17]의해 발견되었다.

${\displaystyle W(x)=frac {1}{\pi }}\int _{0}^{\pi }\log \left(1+xfrac {sin t}{t}e^{t\cot t}\right)dt.}$

주요 지점에는 다음과 같은 연속 분수 표현이 적용됩니다.^[18]

${\displaystyle W(x)=cfrac {x}{1+{\displayac {x}{2+{\displayac {x}{3+{\displayac {17x}{17+{\displayac {x}{\displayac {x}{\displayac {x}}{\displaycfac {x}}{1}{1}{1}}$

또, W(x)< ^[19]1의 경우:

${\displaystyle W(x)=cfrac {x}{\exp {\exp {\exp {\dots }}}}}.}$

다음으로 W(x)> e일 경우

${\displaystyle W(x)=\ln {\ln {\ln {\dots }}}}.}$

기타 공식

확실한 적분

W 함수의 주요 분기와 관련된 몇 가지 유용한 확정 적분 공식은 다음과 같습니다.

${\displaystyle {displaystyle} {{0}^{\pi}W\left(2\cot ^{2}x\right)\sec ^{2}x,sec = 4grt {pi}}.\\[5pt]&\int _{0}^{\infty}{\frac {W(x)}{x{\sqrt {x}}}}}},flac=2sqrt {2\pi}}}.\\[5pt]&\int _{0}^{\infty}W\left({\frac {1}{x^{2}}\right), snf=snfrt {2\pi}}).\end { aligned}}$

첫 번째 항등식은 가우스 적분을 극좌표로 작성함으로써 찾을 수 있습니다.

두 번째 항등식은 다음과 같은 치환 u = W(x)를 만들어 도출할 수 있다.

${\displaystyle {narged}x&=ue^{u},\[5pt]{\frac {narg}{du}}&=(u+1)e^{u}.\end { aligned}}$

따라서

${\displaystyle {displaystyle} {\int _{0}^{\infty}}{x{\sqrt {x}}}}{\frac&=int _{0}{\frac {u}{\fracrt {ue^{u}}}}{\fracrt {u}}}}{\fract {\infty}}{\frcrt {u}}}}{\frcrt {\frt {\frt {\frt {\f}}}}}}{\=\int _{0}^{\infty }{\frac {u+1}{\fracrt {ue^{u}}}du\[5pt]&=\int _{0}^{\infty}{\frac {u+1}{\frac {1}{\fracrt {e^{u}}}}du\[5pt]&^{\infty}w^{-{)tfrac {1}{2}}}e^{-w},filen\[5pt]&=2gamrt {2}}\cdot \Gamma \lefts\tfrac {3}{2}}\right)+{\cdot \tfrac {2}}\gamma \leftsfrac {1}{2}}{2}\right)\\[5pt]&=2grt {2}}\lefts\tfrac {1}{2}}+{\grt {2}}\lefts\grt {pi }}\right)\\[5pt]&=2grt {2\pi }.\end { aligned}}$

세 번째 항원은 치환 u⁻² = x로 함으로써 두 번째 항등식에서 도출할 수 있으며, 첫 번째 항등식은 치환 z = 1/sq2 tan x로 세 번째 항등식에서 도출할 수 있다.

분기 절단(-θ, -1/e)을 따른 z를 제외하고(적분이 수렴되지 않는 경우), Lambert W 함수의 주요 분기는 다음과 같은 ^[20]적분으로 계산할 수 있습니다.

${{displaystyle {begin{aligned}W(z)&=snotfrac {z}{2\pi}}\int _{-\pi}^{\frac {좌(1-\nu \cot \nu \right)^2}+nu ^{2}}{z+\nu \cscot nu e^{-nu\nu\cot } \cot nu \cot } } } } int,$

여기서 두 적분 표현은 적분도의 대칭으로 인해 동등하다.

부정 적분

적용들

방정식을 풀다

Lambert W 함수는 알 수 없는 양이 기저값과 지수, 또는 로그의 내부와 외부 모두에서 발생하는 방정식을 푸는 데 사용됩니다.전략은 이러한 방정식을 ze = w의 형태로^z 변환한 다음 W 함수를 사용하여 z에 대해 푸는 것입니다.

예를 들어, 방정식은

${\displaystyle 3^{x}=2x+2}$

(여기서 x는 알 수 없는 실수)는 다음과 같이 고쳐 쓰면 해결할 수 있습니다.

$\ displaystyle { arigned } = 3^ { - x } { } = 3^ { - x - 1 } = - { \ frac { 6 } \ \ \ \ \ \ \ \ \ rightarrow \ ( \ ln 3 ) ( x - 1 ) e - { ln 3 （ ln )$

이 마지막 방정식은 원하는 형태를 가지며, 실수 x에 대한 해는 다음과 같습니다.

${\displaystyle(\ln 3)(-x-1)=W_{0}\left({\frac {-\ln 3}{6}}\오른쪽)\\\\(\ln 3)(-x-1)=W_{-1}\left({\frac {-\ln 3){6}}\right)}$

그 결과, 다음과 같이 됩니다.

${\displaystyle x=-1-{\frac {W_{0}\left(-{\frac {ln 3}})}{\ln 3}=-0.79011\ldots \{textrm {or}\x=-1-{W_{-1}\left(-{\frac {6}\frac}) {\ln}3}{6}}}} {\ln}$

일반적으로는,

${\displaystyle x=a+b,e^{cx}}$

다음과 같습니다.

${\displaystyle x=a-{\frac {1}{c}}W(-bc,e^{ac})}$

여기서 a, b, c는 복소수이고 b와 c는 0이 아니며 W 함수는 임의의 정수 순서입니다.

비스코스 흐름

입상 및 파편 흐름 전면과 퇴적물, 그리고 자연현상 및 실험실 실험에서의 점성 유체의 전면은 다음과 같이 램버트-울러 오메가 함수를 사용하여 설명할 수 있다.

${\displaystyle H(x)=1+W\left(H(0)-1)e^{(H(0)-1)-{\frac {x}{L}}}\right)}}$

여기서 H(x)는 잔해 흐름 높이, x는 채널 다운스트림 위치, L은 흐름, 흐름 높이 및 유압 구배의 여러 물리적 및 기하학적 매개변수로 구성된 통합 모델 매개변수입니다.

파이프 흐름에서 Lambert W 함수는 Darcy 마찰 계수를 구하기 위한 콜브룩 방정식의 명시적 공식의 일부이다.이 계수는 흐름이 ^[21]난류일 때 파이프 직선을 통해 압력 강하를 결정하는 데 사용됩니다.

단순 분기 유압 시스템의 시간 의존 흐름

램버트 W 함수의 주요 분기는 원심 ^[22]펌프를 사용하여 자유 표면 수준이 다른 두 저장고 사이의 뉴턴 유체의 시간 의존적 전달을 연구하는 기계 공학 분야에서 사용되었다.Lambert W 함수는 층상 및 난류 양면에서 유체의 유량에 대한 정확한 솔루션을 제공하였다.

${\displaystyle Q_{turb}=frac {Q_{i}}{\zeta _{i}}}W_{0}\left [\zeta _{i},e^{(\zeta _{i}+\beta t/b)}\right]}$

${\displaystyle Q_{lam}=frac {Q_{i}}{\xi _{i}}}W_{0}\left [\xi _{i}, e^{\left(\xi _{i}+\beta t/(b-\Gamma _{1}\right)}\right]}$

$여기$서 $(\$})는 초기 유량이고 t$(\displaystyle$ t$)$는 시간입니다.

신경 영상 촬영

Lambert W 기능은 뇌 복셀 내의 뇌 혈류 및 산소 소비 변화를 해당 혈중 산소 수준 의존(^[23]BOLD) 신호에 연결하기 위해 신경 영상 분야에서 사용되었다.

화학 공학

Lambert W 함수는 전기화학적 에너지 저장을 위한 유리 탄소 기반 슈퍼 캐패시터의 다공질 전극막 두께를 모델링하기 위해 화학 공학 분야에서 사용되었다.Lambert W 함수는 탄소막의 성장과 같은 막의 연소가 서로 ^[24][25]경쟁하는 기상 열활성화 과정의 정확한 솔루션임이 밝혀졌다.

재료과학

램버트 W 함수는 임계 전위 개시막 두께를 결정하기 위해 에피택셜막 성장 분야에서 사용되었다.이는 에피택셜 필름의 계산된 두께로, 열역학 원리로 인해 필름에 저장된 탄성 에너지를 최소화하기 위해 결정학적 전위가 발생합니다.이 문제에 대해 램버트 W를 적용하기 전에, 임계 두께는 암묵적 방정식을 풀어서 결정되어야 했다.Lambert W는 이를 분석적 취급을 위한 명시적 방정식으로 ^[26]쉽게 전환합니다.

다공질 매체

그 램버트 W함수 유체의 흐름의 분야에서 다공 인터페이스는 상수 딥, 그리고 두께의 무거운 액체, 맨 안쪽 끝 부분에 주사하였고, 같은 비율로에서 생산된 라이터와 바뀔 때 단일 민족 다공성 침대에서 2중력으로 분리된 유체 분리의 기울임 모델에 고용되어 있었다.M이 있구.만약 변위는 무거운 액은 라이터 액을 보이고 있어 불안정한 세계−1 지점을 적용하는 솔루션의 주요 지점 안정적인 변위에 해당합니다.[27]

베르누이 수와 토드속

그 방정식(베르누이 수는 기능과 토드 genus로 연결되어):.

${\displaystyle Y={\frac{X}{1-e^{X}}}}$

두 진짜 가지 W0과 W−1의 방법으로:해결될 수 있습니다.

${\displaystyle X(Y)={\begin{경우}W_ᆮ\left(Ye^{Y}\right)-W_ᆯ\left(Ye^{Y}\right)=Y-W_ᆰ\left(Ye^{Y}\right)&,{\text{에}}Y<, -1,\\W_ᆲ\left(Ye^{Y}\right)-W_ᆳ\left(Ye^{Y}\right)=Y-W_ᆴ\left(Ye^{Y}\right)&,{\text{에}}-1<.Y<0.\end{경우}}}$

이 응용 프로그램에서는 W함수의 가지 차이 순서대로 다른 초월 방정식 고용될 수 있을 것을 보여 준다.[28]

통계 정보

막대 세트에 symmetrized Kullback–Leibler 발산(또한 제프리스 발산이라고 불렀다[29])에 관련하여 정의되의 중심에 따라 닫힌 형태는 램버트 W함수를 사용하고 있다.[30]

감염성 질환에 대한 테스트

그래서 적어도 한 개체 감염되는 램버트 W함수가 최적 집단의 크기에 수영장 시험에 해결.[31일][32][33]

슈뢰딩거 방정식의 정확한 해

그 램버트 W함수는 조화 진동자 플러스 centrifugal의 옆에 있는 5–를 이어가고 있는 양자 역학의 잠재력은 쿨롱과 역 제곱, 모스, 역 제곱 근는 고정형 1차원 슈뢰딩거 방정식에 합류하는 초 기하 func의 관점에서 잠재적인– 정확한 해답에 나타납니다.Tions. 그 잠재력으로 제시한다.

$({displaystyle V=v_{0}}{1+W\left(e^{-{\frac {x}{\frac }}}\right)}).}$

해법의 특이점은 슈뢰딩거 방정식의 일반적인 해법을 구성하는 두 개의 기본 해 각각이 비례하는^[34] 인수의 두 개의 합초기하함수의 조합에 의해 주어진다는 것이다.

$\displaystyle z=W\left(e^{-{\frac {x}{\frac }}\오른쪽).}$

Lambert W 함수는 또한 더블 델타 퍼텐셜을 가진 1차원 슈뢰딩거 방정식의 결합 상태 에너지에 대한 정확한 해에도 나타납니다.

아인슈타인 진공 방정식의 정확한 해

아인슈타인 진공 방정식의 슈바르츠실트 계량 해법에서, W 함수는 에딩턴-핀켈슈타인 좌표를 슈바르츠실트 좌표로 이동하기 위해 필요하다.이러한 이유로 Kruskal-Szekeres 좌표 구성에도 나타난다.

델타 셸 전위의 공명

델타 셸 전위의 s파 공명은 정확히 Lambert W ^[35]함수의 관점에서 기록될 수 있다.

열역학 평형

반응물에 온도와 일정한 열용량을 가진 제품이 관련되면 평형상수 K가 준수된다.

${\displaystyle\ln K=frac {a}{T}}+b+c\ln T}$

일부 상수 a, b 및 c의 경우.c(δC_p/R과 동일)가 0이 아닌 경우 T의 값을 구할 수 있습니다.여기서 K는 소정의 값과 같으며 Ln T에 L을 사용합니다.

${\displaystyle {aligned}-a&=(b-\ln K)T+cT\ln T\=(b-\ln K)e^{L}+cLe^{L}\\[5pt]-{\frac {a}{c}}&=\leftfrac {b-\ln K}{c}}+L\right)e^{L}\[5pt]-{\frac {a}{c}}e^{\frac {b-\ln K}{c}}&=left(L+{\frac {b-\ln K}{c}}\right)e^{L+{\frac {b-\ln K}{c}}\[5pt]L&=W\left(-{\frac {a}{c}}e^{\frac {b-\ln K}{c}}\right)+{\frac {\frac {\ln K-b}{c}}\[5pt]T&=\exp \left(W\left(-{\frac {a}{c}}e^{\frac {b-\ln K}{c}}\right)+{\frac {ln K-b}{c}}\right}).\end { aligned}}$

a와 c의 부호가 같을 경우, 2개의 솔루션이 존재하거나 존재하지 않습니다(또는 W의 인수가 정확히 -1/e인 경우에는 1개).(상부 솔루션은 관련이 없을 수 있습니다.)만약 그들이 정반대의 부호를 가지고 있다면, 하나의 해결책이 있을 것이다.

고분자 혼합물의 상분리

에드먼드-오그스턴 모델에 따라 열역학적으로 불호환 폴리머 혼합물의 위상도를 계산할 때, 2항 및 타이라인 용액은 램버트 W ^[36]함수로 공식화된다.

D차원 우주에서의 빈 변위 법칙

빈의 변위 법칙은 ${\displaystyle {is}_{}max}$ / T ${\displaystyle =}$ ${\displaystyle \alpha }$ ${\displaystyle =}$ ${\displaystyle \mathrm{c}}$ ${\displaystyle \mathrm{on}}$ ${\displaystyle \mathrm{s}}$t { $display \nu$ _ { \ $max$} / T$$= \ $alpha$= \ $mathrm$ {$const$ 로 표현됩니다.${\displaystyle x}$ ${\displaystyle =}$ ${\displaystyle h_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle max{}_{}}$ / $k$ { $display$ x =$$h$\nu$ _ { \ max } / k _ { \ max $}$ / k _ { t } { t } { t } } } } } } w { t } } w mathrm ${$brm { t }$aystyle \rho$ _${T}}$는 스펙트럼 에너지 밀도이며${\displaystyle {,}^{}}$ e - ${\displaystyle x^{}}$ $=$ - ${\displaystyle x\frac{}{}}$ ${\displaystyle \frac{D}{}}${ $displaystyle$ e$^{-x$}=1 - {\$frac {x}{D$를 $찾을{\displaystyle {}^{}}$ 수 있다.$솔루션{\displaystyle }$ x ${\displaystyle =D}$ +${\displaystyle W}$( - ${\displaystyle {}^{}}$e -${\displaystyle {}^{}{D}^{}}$) \ $displaystyle$ x =$D+$$W\left(-De^{-D}\right)$는 스펙트럼 에너지 밀도가 우주의 ^[37]차원에 의존함을 보여준다.

AdS/CFT 대응

거대 마그논, 단일 스파이크 및 GKP 문자열의 분산 관계에 대한 전형적인 유한 크기 보정은 Lambert W ^[38][39]함수로 표현될 수 있다.

역학

SIR 모델의 t → δ 한계에서 민감하고 회복된 개인의 비율은 Lambert W ^[40]함수의 관점에서 솔루션을 가진다.

발사체의 비행시간 결정

속도에 비례하는 공기 저항을 경험하는 발사체의 총 이동 시간은 Lambert W 함수를 사용하여 정확한 형태로 결정할 수 있습니다.

전자 표면파 전파

원통형 금속 와이어를 전파하는 전자축 대칭 표면파(저감압 단일 TM01 모드)의 전파파수 결정에 나타나는 초월 방정식은 u ln = v(u와 v가 문제의 기하학적 및 물리적 요소를 함께 뭉치는 경우)와 같은 방정식을 일으킨다.이는 Lambert W 함수에 의해 해결됩니다.1898년경 소머펠트 때문에 이 문제에 대한 첫 번째 해법은 이미 램버트 W ^[41]함수의 값을 결정하기 위한 반복 방법을 포함하고 있었다.

실제 타원의 직교 궤적

(${\displaystyle 0,}$ $)$을${\displaystyle }$중심으로 한 $타원{\displaystyle {}^{}}$ x${\displaystyle {}^{}{2\mathrm{}}^{}}$+ (${\displaystyle {}^{}}$- ${\displaystyle {2\mathrm{}}^{}}$2 ) ${\displaystyle {y\mathrm{}}^{}}$ 2 ${\displaystyle {}^{}}$ ${\$ ${\displaystyle {2\mathrm{}}^{}}$ { { $display style$ x$^$ { 2 }$$+ ( $1$- \ $varepsilon$^ {2$}$ = \ $varepsilon$^ {2$} =$ \ $display style$ $( 0$ ,$0$ )는 직교 궤적의$이심률$에 의해 파라미터화됩니다$.$${\displaystyle (}$ ${\displaystyle 1\frac{\mathrm{}}{}\frac{y}{}}$ +${\displaystyle }$$y$ )${\displaystyle d}$ y ${\displaystyle =}$ ( ${\displaystyle 1\frac{\mathrm{}}{}x}$ -${\displaystyle }$x )$d$x x ( \ $displaystyle$ $\ frac$ {$}$${\displaystyle }${ $y$${\displaystyle {}_{}}$$$$}$ +$y$ \ right ) $dy$= \$left frac$ { ${\displaystyle {}^{}}$$}$ - x \ $right$ )$$${\displaystyle {dy}^{}}$ $=$ W${\displaystyle {}_{}{0\mathrm{}}_{}}$ ( ${\displaystyle {}^{}}$ ${\displaystyle \exp -{2\mathrm{}}^{}}$)

일반화

표준 Lambert W 함수는 다음과 같은 형태의 초월 대수 방정식(x)에 대한 정확한 해를 표현한다.

$${\displaystyle e^{-cx}=a_{0}(x-r)}$$

(1)

여기서₀ a, c 및 r은 실수 상수입니다.해결책은

Lambert W 함수의^[42][43][44] 일반화는 다음과 같습니다.

• 저차원에서의 일반상대성이론과 양자역학(양자중력)에 대한 적용. 사실 이 두 영역 사이의 링크(2007년 이전에는^[45] 알려지지 않음)이며, 여기서 (1)의 오른쪽이 x의 2차 다항식으로 대체된다.

  $$\displaystyle e^{-cx}=a_{0}\left(x-r_{1}\오른쪽)\left(x-r_{2}\오른쪽)}$$

  (2)

  여기서₁ r과₂ r은 2차 다항식의 근인 실제 고유 상수입니다.여기서 해는 단일 인수 x를 갖는 함수이지만, r과₀ a와 같은_i 항은 그 함수의 파라미터이다.이 점에서 일반화는 하이퍼기하 함수와 메이저 G 함수와 유사하지만 다른 종류의 함수에 속합니다.r = r일₂ 때₁, (2)의 양쪽을 인수분해 (1)로 줄일 수 있으며, 따라서 용액은 표준 W 함수로 감소한다.등식 (2)는 동일하지 않은 정지 질량의 경우 R = T 또는 선형 2체 중력 문제의 메트릭을 1 + 1 차원 (1 공간 차원 및 1 시간 차원)에서 도출하는 딜라톤 장을 지배하는 방정식과 양자 기계 이중 웰 디락 델타 모델의 고유 에너지.균일하지 않은 전하입니다.

• 양자역학적 삼체문제의 특수한 경우, 즉 (3차원) 수소 ^[46]분자 이온의 고유 에너지 해석 솔루션.여기서 (1)의 오른쪽은 x의 무한 차수 다항식의 비율로 대체된다.

  $${\displaystyle e^{-cx}=a_{0}{\frac {displaystyle \infty _{i=1}^{\infty }(x-s_{i}){\displaystyle \infty }(x-s_{i})}}}$$

  (3)

  여기서_i r과_i s는 별개의 실수 상수이고 x는 고유 에너지와 핵간 거리 R의 함수이다.(1) 및 (2)에 나타내는 특수한 경우의 식 (3)은 대규모 지연 미분방정식과 관련되어 있다.G. H. Hardy의 "허위 도함수"^[47] 개념은 (3)의 특수한 경우에 정확한 다중 뿌리를 제공한다.

근본적인 물리적 문제에서 Lambert W 함수의 적용은 원자, 분자 및 ^[48]광학 물리학 영역에서 최근에 본 (1)의 표준 사례에서도 고갈되지 않는다.

플롯

• 복소 평면에서 Lambert W 함수의 그림
• 

  z = Re(W₀(x + iy))

• 

  z = Im(W₀(x + iy))

• 

  z = W₀(x + iy)

• 

  이전 세 개의 플롯

수치평가

W 함수는 뉴턴의 방법을 사용하여 w = W(z)(so z = we^w)에 대한 연속적인 근사치를 사용하여 근사할 수 있다.

$({displaystyle w_{j+1}=w_{j}-{\frac {w_{j}e^{w_{j}-z}{e^{w_{j}}+w_{j}e^{w_{j}}})}$

W 함수는 Halley의 방법을 사용하여 근사할 수도 있다.

$\displaystyle w_{j+1}=w_{j}-{\frac {w_{j}-z}{e^{w_{j}-left(w_{j}+1\right)-{\dfrac {left(w_{j}+2\right)\left(w_{j}_j}-z}-{j}-right)$

W를 계산하기 위해 Corless ^[2]등에 주어졌다.

$실제{\displaystyle }$ x$$δ -${\displaystyle 1}$/$$$e의 경우$ R의 2차 $레이트$ 재귀 공식으로 근사할 수 있습니다.이아코노와 J.P.보이드:^[49]

$({displaystyle w_{n+1}(x)=black {w_{n}(x)}{1+w_{n+1}(x)}}\left(1+\log \log \left\flac {x}{w_{n}(x)}}\right).}$

Lajos Loczi는 $적절한{\displaystyle {}_{}}$ w ${\displaystyle {0\mathrm{}}_{}}$(${\displaystyle x}$ $){displaystyle w_{0}(x$을 선택함으로써 다음과 같이 증명합니다.

• $if{\displaystyle }$ x${\displaystyle （e}$ , ${\displaystyle \infty }$ )$$） { $displaystyle$x \$in$ ( $e$, \ $infty$)$$} : $w{\displaystyle {}_{}{0\mathrm{}}_{}}$ (${\displaystyle x}$ )${\displaystyle =}$ ${\displaystyle \log （x}$) - ${\displaystyle \log （}$ log$$、 \$log$ ( x )${\displaystyle }$、 \ $displaystyle$ w$_ 0 =$ \ $log$($$x )$$、 \ log ( x ) }
• $if{\displaystyle }$ x ${\displaystyle (}$ ( ${\displaystyle 0}$,${\displaystyle e}$)$$: \ $display style$ x \ $in$( $0$, e$$) :}${\displaystyle {}_{}{w}_{}}$ ${\displaystyle 0}$( x )${\displaystyle =}$ $x$/$$e , { $displaystyle$w _ {$0$（$$x ) = x /$e$ , }
• $if{\displaystyle }$ x ${\displaystyle (}$( -${\displaystyle 1}$ /${\displaystyle e}$ ,${\displaystyle 0}$)$$: {\$displaystyle$ x$\in$ (-$1/e,0)$ :}
  • 주요 $브랜치{\displaystyle {}_{}}$ ${\displaystyle {W\mathrm{}}_{}}$ 0$(\$$displaystyle{\displaystyle {}_{}}$ $W_{0$ w ${\displaystyle {0\mathrm{}}_{}x)}$ ${\displaystyle =}$ ${\displaystyle e\frac{}{}}$ ${\displaystyle \frac{x}{1}}$ + ${\displaystyle \frac{\sqrt{e}x}{}}$ x +${\displaystyle \frac{\sqrt{}1\sqrt{\mathrm{}}}{}}$ + ${\displaystyle \sqrt{e}}$ x ${\displaystyle \mathrm{로그}(}$( ${\displaystyle 1\sqrt{\mathrm{}}}$+ ${\displaystyle \sqrt{1}}$ +${\displaystyle }$e${\displaystyle }$x )$$、 \ $displaystyle w$_ $0$（ x ） =$frac { 1$ + $ex$} { 1 + $rt { 1$ + 1 + e x } } } } } }$$、 \$log$ ( 1 ) 、
  • ${\displaystyle {\mathrm{W}}_{}}$- 1$({${-1$\}):$
    • ${\displaystyle {w\mathrm{}}_{}}$ ${\displaystyle 0{}_{}}$(${\displaystyle }$x ) $=$ -${\displaystyle 1}$ -${\displaystyle \sqrt{}2\sqrt{\mathrm{}}}$ ($1$ + ${\displaystyle \sqrt{ex}}$)$$, $x$${\displaystyle \in }$ $x{\displaystyle }$ ${\displaystyle （}$ -${\displaystyle }$$1$${\displaystyle }$/ ${\displaystyle \mathrm{e}}$,${\displaystyle }$- ${\displaystyle 1\mathrm{}}$ / 4${\displaystyle ）}$ , { \ display style$$$x$\ $in$( - 1 / ${\displaystyle e}$ , 1 / 4 )$$} $、$ { \ $display style$ x \ $in$ ( -$1$ / $e ,$ 1 / 4 )$$}
    • ${\displaystyle {w\mathrm{}}_{}}$ ${\displaystyle 0{}_{}}$(${\displaystyle }$x ) $=$ ${\displaystyle \log }$ ${\displaystyle }$ (${\displaystyle }$( -${\displaystyle x}$) - ${\displaystyle \log }$ ${\displaystyle }$ -${\displaystyle }$(${\displaystyle }$-${\displaystyle x}$) , x$$${\displaystyle 、}$ \ $display style$ w$_$ 0 （$$x$）$- \ $log sparamx$ ) - \ log sparams \ $log sparx$ )$$、 $x$ （ - 1${\displaystyle }$/ ${\displaystyle 4}$,$0$）$$、 { $display style$x \ $in$( -$1$/ 0 )$$} } } 。

모든 ^[50]정밀도에 대해 반복 단계의 최대 수를 미리 결정할 수 있습니다.

• $if{\displaystyle }$ x ${\displaystyle (}$( ${\displaystyle e}$ , ${\displaystyle )}$ )$${ $display style$x \$in$( e , \$infty$ ) }$$ ( Theorem . ): < ( ) - n() < (+ /e )2 n, { $display style 0$ < W _$0 }$ ( x ) < 1 /$w$ _ n$}$ ( log ) < 1 / 1 / 1 ( $log$（ log ) \ leftime ) \ leftw _ left left left left$)$
• ${\displaystyle \mathrm{if}}$ x${\displaystyle ,}$ (${\displaystyle 0}$ , $e$) { $style x$ $\ in$ ( $0$, e ) $$（ Theorem 2 . 9 ） : < ( ) - ( x )<( -1 / ) - 1 , \ $display$0 < $W _ 0$( x ) -$w$ _ n（ x ) （ x ) <\$fright ）$
• $if{\displaystyle }$ x ${\displaystyle (}$( -${\displaystyle 1}$ /${\displaystyle e}$ ,${\displaystyle 0}$)$$: {\$displaystyle$ x$\in$ (-$1/e,0)$ :}
  • 주요 $브랜치{\displaystyle {}_{}}$ ${\displaystyle {W\mathrm{}}_{}}$ 0$({$ W_${0})($Theorem 2.17) : < () - ()< ( 1/ n, \ $display 0$ < $w$_ { $n }$ ( x ) -$W _ 0$( x ) < \ $left ( 1$ / $10$\ $right$)^ { $n$} } } 。
  • $브런치{\displaystyle {}_{}}$W - $({-$$Theorem$ 2.23) : < - () - ()< ( /) n .( \ $display style$0 < $W$_ { _ 1 $($ x ) - $w$ { $n }$ ( x ) <\$left$ ($1$ /$2$ \ 2 \ right )^ { n$}$ } 。$}$

소프트웨어

Lambert W 함수는 다음과 같이 구현됩니다.LambertW메이플에서^[51] lambertwGP(및glambertWPARI에서)lambertwMatlab에서도^[52]lambertw와 옥타브 음으로specfun패키지, 로서lambert_w맥시마에서는^[53]ProductLog(사일런트 에일리어스 포함)LambertW)^[54]는 Mathematica에서 다음과 같이 표시됩니다.lambertwPython scipy의 특수 함수 ^[55]패키지에 포함되어 있습니다.LambertWPerl's에서는ntheory모듈 및 ^[56]asgsl_sf_lambert_W0,gsl_sf_lambert_Wm1GNU Scientific Library(GSL)의 특수 기능 섹션에서 기능을 수행합니다.Boost C++ 라이브러리에서 콜은 다음과 같습니다.lambert_w0,lambert_wm1,lambert_w0_prime,그리고.lambert_wm1_primeR에서, Lambert W 함수는 다음과 같이 구현됩니다.lambertW0그리고.lambertWm1의 기능lamW패키지.^[57]

복잡한 Lambert W 함수의 모든 분기에 대한 C++ 코드는 Istvann Mező ^[58]홈페이지에서 이용할 수 있다.

「 」를 참조해 주세요.

• 라이트 오메가 함수
• 램버트의 삼항 방정식
• 라그랑주 반전 정리
• 실험 수학
• 홀스타인청어법
• R = T 모델
• 로스 레마

메모들

레퍼런스

• Corless, R.; Gonnet, G.; Hare, D.; Jeffrey, D.; Knuth, Donald (1996). "On the Lambert W function" (PDF). Advances in Computational Mathematics. 5: 329–359. arXiv:1809.07369. doi:10.1007/BF02124750. ISSN 1019-7168. S2CID 29028411. Archived from the original (PDF) on 2010-12-14. Retrieved 2007-03-10.
• Chapeau-Blondeau, F.; Monir, A. (2002). "Evaluation of the Lambert W Function and Application to Generation of Generalized Gaussian Noise With Exponent 1/2" (PDF). IEEE Trans. Signal Process. 50 (9). doi:10.1109/TSP.2002.801912. Archived from the original (PDF) on 2012-03-28. Retrieved 2004-03-10.
• Francis; et al. (2000). "Quantitative General Theory for Periodic Breathing". Circulation. 102 (18): 2214–21. CiteSeerX 10.1.1.505.7194. doi:10.1161/01.cir.102.18.2214. PMID 11056095. S2CID 14410926. (Lambert 함수는 인간 질병에서 지연-차동역학을 해결하기 위해 사용됩니다.)
• Hayes, B. (2005). "Why W?" (PDF). American Scientist. 93 (2): 104–108. doi:10.1511/2005.2.104.
• Roy, R.; Olver, F. W. J. (2010), "Lambert W function", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
• Stewart, Seán M. (2005). "A New Elementary Function for Our Curricula?" (PDF). Australian Senior Mathematics Journal. 19 (2): 8–26. ISSN 0819-4564.
• Veberic, D., "Lambert W(x) 함수로 즐거운 시간" arXiv:1003.1628(2010);
• Chatzigeorgiou, I. (2013). "Bounds on the Lambert function and their Application to the Outage Analysis of User Cooperation". IEEE Communications Letters. 17 (8): 1505–1508. arXiv:1601.04895. doi:10.1109/LCOMM.2013.070113.130972. S2CID 10062685.

외부 링크

• 미국 국립과학기술원 디지털 라이브러리– Lambert W
• Math World – Lambert W-함수
• Lambert W 함수 계산
• 콜리스 등Lambert W 연구에 대한 참고 사항
• Halley와 Fritch의 반복을 사용한 GPL C++ 구현.
• GNU 과학 라이브러리의 특수 기능 – GSL