격자망

이 기사는 위키피디아의 품질 기준을 충족시키기 위해 정리가 필요할 수 있다.구체적인 문제는 수학 공식의 형식이다. 가능한 경우 이 문서를 개선하는 데 도움을 주십시오. (2018년 3월) (이 템플리트 메시지를 제거하는 방법과 시기 알아보기)

대칭 격자는 대각선 교차 션트 요소가 존재하는 2포트 전기파 필터로, 래더 네트워크와 구별되는 구성이다.격자의 구성요소 배치는 아래 도표에 나타나 있다.이 회로의 필터 특성은 처음에는 이미지 임피던스 개념을 이용하여 개발되었으나, 나중에는 네트워크 분석의 보다 일반적인 기법을 적용하였다.

"시리즈 임피던스"(Za의 인스턴스)와 "션트 임피던스"(Zb의 인스턴스)가 모두 두 번 발생하기 때문에 격자망에는 구성요소가 중복되어 있는데, 이는 다양한 응답으로 회로 설계자에게 향상된 유연성을 제공하는 배열이다.격자 네트워크는 격자 요소의 구성요소 선택에 ^{[4]: 412} 따라 지연 네트워크,^[1] 진폭 또는 위상 교정 네트워크,^[2] 분산 네트워크 또는 선형 위상 필터의 특성을 가질 수 있다.

배열

대칭 격자의 기본 구성은 좌측 다이어그램에 표시된다.일반적으로 사용되는 단기 버전이 오른쪽에 표시되며, 두 번째 쌍의 일치하는 임피던스가 있음을 나타내는 점선이 표시된다.

이 회로에서는 래더 필터 구조에서는 사용할 수 없는 ^[5]특징인 전송 속성과 독립적으로 지정된 특성 임피던스를 가질 수 있다.또한 회로의 다양한 회로 특성에 대한 상시 저항 네트워크로 설계할 수 있다.

격자 구조는 접지면이 있는 회로에 삽입하기 위해 불균형한 형태(아래 참조)로 변환할 수 있다.이러한 변환은 또한 구성요소 수를 줄이고 구성요소 허용오차를 완화한다.^[6]

Wheatstone 브리지 구성에서^[7] 격자를 다시 그릴 수 있다(기사 조벨 네트워크 참조).단, 격자 필터의 특성, 특히 계단식 필터의 동작을 조사할 수 있는 편리한 형식이 아니다.

기본 속성

이미지 이론의 결과

필터 이론은 처음에 전송 라인의 초기 연구에서 개발되었다.^[8][9]이 이론에서 필터 부분은 그 전파 상수와 영상 임피던스(또는 특성 임피던스)의 관점에서 지정된다.

특히 격자, 전파 함수 및 특성 임피던스는 다음에 의해 정의된다.^{[4]: 379 [6]}

${\displaystyle \gamma =\ln \left[{\frac {\sqrt {{\frac {Z_{a}}{Z_{b}}}+1}}{\sqrt {{\frac {Z_{a}}{Z_{b}}}-1}}}\right]=2\tanh ^{-1}\left({\sqrt {\frac {Z_{a}}{Z_{b}}}}\right)\qquad {\text{and}}\qquad Z_{0}={\sqrt {Z_{a}Z_{b}}}}$

$일단\frac{{}_{}}{}$ 선택되고 Z $\frac{a_{}}{}$ $\frac{{}_{}}{{}_{}}$ $\frac{b_{}}{}$ ${\$와 ×의 특성을 각각 확인할 수 있는 솔루션을 찾을 수 있다.(실제에서는 및 에 대해 물리적으로 실현 가능한 장애를 초래하는 선택 및 선택으로 제한된다.)필터 회로가 하나 이상의 통과 대역과 여러 개의 정지 대역(또는 감쇠 영역)을 가질 수 있지만 여기서는 단일 통과 대역의 네트워크만 고려한다.

회로의 통과 대역에서 제품 ×는 진짜(즉, 저항성)이며, 필터의 종단 저항과 동일할 수 있다.그렇게

${\displaystyle Z_{a}Z_{b}=R_{0}^{2}\qquad {\text{or}}\qquad {\frac{{R_{0}}}={\frac {R_{0}}}{Z_}}}\qquad{\text{(통과대역의 주파수)}}}$

즉, 임피던스는 이 주파수 범위 내에서 서로의 이중으로 작용한다.

필터의 감쇠 범위에서 필터의 특성 임피던스는 순수하게 가상이며,

${\displaystyle Z_{a}=Z_{b}\qquad \qquad \qquad {\text{(감쇠 대역의 주파수)}}}$

따라서 특정 특성을 달성하기 위해 및 내부의 반응성을 선택함으로써 이들의 공명 주파수와 반저항 주파수가 패스밴드에서는 서로 이중이고 스톱밴드에서는 서로 일치하도록 한다.한 조건 집합에서 다른 조건으로의 변경이 발생하는 필터의 전환 영역은 및 의 복잡성을 증가시킴으로써 필요한 만큼 좁게 만들 수 있다.통과 대역에서 필터의 위상 응답은 및 의 공명 주파수와 반저항 주파수의 위치(스페이스)에 의해 제어된다.

편의상, 정규화된 파라미터는 다음과 같이 정의된다.

${\displaystyle y_{0}={\sqrt{Z_{b}}}}{Z_{b}}}}}}}{\sqrt{z_{b}}}}}}}}}{\sqqrt {z_{b}}}}}}}}}}}}}}}}}{\sqrt}}}}}}}}}}}}}}}}}}}}}}}}}}$

여기서 정규화된 값 = / 및 = /가 도입되었다.매개변수를 지수함수와 정규화된 네트워크의 특성 임피던스라고 한다.감쇠 영역과 전송 영역의 매개변수와 대략적인 일치.^{[4]: 383}

격자의 계단식

모든 고차 격자망은 그들의 특성 임피던스가 모두 원래의 그것과 같고 그들의 전파 기능의 합이 원본과 같다면 더 단순한 격자들로 대체될 수 있다.^{[4]: 435}

특히 올패스 네트워크(위상 특성만 수정하는 네트워크)의 경우, 주어진 네트워크는 항상 하나의 1차 주문 격자와 함께 2차 주문 격자의 계단식 격자로 대체될 수 있다.^[6]

필터 요구사항이 무엇이든, 감소 프로세스는 보다 단순한 필터 구조를 생성하며, 구성 요소 공차에 대한 요구는 덜 엄격해진다.^[6]

이미지 이론의 단점

영상 이론에 의해 예측된 필터 특성은 올바르게 종료된 네트워크를 필요로 한다.필요한 종료를 달성하기 어려운 경우가 많기 때문에 저항기를 종단부로 사용하는 경우가 많아 필터가 일치하지 않는 경우가 많다.따라서 회로의 예측 진폭과 위상 반응은 더 이상 이미지 이론이 예측하는 대로 되지 않을 것이다.예를 들어 컷오프 주파수 근처에서 불일치가 가장 심한 저역 통과 필터의 경우 통과 대역에서 정지 대역으로의 전환은 예상보다 훨씬 덜 날카롭다.

아래 그림은 문제를 예시하고 있다.상수 k 저역-통과 필터의 2개 섹션에 해당하는 격자 필터는 이미지 방법에 의해 도출되었다.(네트워크는 정상화되고, 1과 1은 = 1과 1이므로 = √L / = 1과 = 2√L × = 2가 된다.왼쪽 그림은 격자 회로를, 오른쪽 그림은 네트워크가 종료된 상태에서 (1) 저항적으로, (2) 정확한 특성 임피던스에 삽입 손실을 준다.

불일치 문제를 최소화하기 위해 오토 율리우스 조벨 등에 의해 다양한 형태의 이미지 필터 엔드 종료를 제안했지만, 불가피한 타협으로 인해 방법이 유리하지 않게 되었다.그것은 네트워크 분석과 네트워크 통합의 보다 정확한 방법으로 대체되었다.^{[10][11][12][13]}

네트워크 분석에 의해 도출된 결과

이 다이어그램은 대칭 격자의 일반 회로를 보여준다.

회로의 메쉬 분석이나 노달 분석을 통해 완전한 전달 기능을 찾을 수 있다.

$디스플레이 스타일(\displaystyle {\\displaystyle}}}}\qquad {\v_{\text{out}}}{v_{\text{in}}}}={\frac {Z_{L}(Zb-Za)}{(Z_{S}+Z_{L})+2(ZaZB+Z)+2(ZaZB+Z_)_}{S}Z_{L}}}}}$

네트워크의 입력 및 출력 임피던스(Z_in 및 )는 다음과 같다.

${\displaystyle Z_{\text{in}={\frac {2ZaZb+Z_{L}(Za+Zb)}{Za+Zb+2Z_{L}}\qquad {\text{and}}\qquad Z_{\text{out}}={\frac {2ZaZb+Z_{S}(Za+Zb)}}{Za+Zb+2Z_{S}}}$

전파함수가 네트워크의 일치 특성 임피던스일 때만 정확하게 성능을 예측하는 영상 이론과 달리, 이러한 방정식은 모든 실현 가능한 임피던스 값에 대해 정확하다.

방정식은 여러 가지 가정을 함으로써 단순화할 수 있다.첫째로, 네트워크는 종종 같은 값의 저항기에 의해 소싱되고 종단되어, =가 되고 방정식이 된다.

${\displaystyle {\frac {v_{\text{out}}}{v_{\text{in}}}}={\frac {R_{0}(Zb-Za)}{2(Za+R_{0})(Zb+R_{0})}}\qquad {\text{and}}\qquad Z_{\text{in}}=Z_{\text{out}}={\frac {2Za\,Zb+R_{0}(Za+Zb)}{Za+Zb+2R_{0}}}}$

둘째, 장애물과 상호의 이중인 경우, × = , 더 단순화할 수 있다.

${\displaystyle {\frac {v_{\text{out}}}{v_{\text{in}}}={\frac {(R_{0}-Za)}{2(R_{0}+Za)}}}}}}={\frac {(Zb-R_{0}+Zb)}{2(R_{0}+Zb)}}}\qquad {\and}\qquad Z_{\in}}=Z_{\text}}{\text}}}={\text}}}=}=R_{0}}$

그래서 그러한 네트워크는 상시 접속 네트워크다.

마지막으로, 표준화된 네트워크의 경우 = 1을 사용하여

${\displaystyle {\frac {v_{\text{out}}}{v_{\text{in}}}={\frac {(1-z_{a})}{2(1+z_{a})}}}}={\frac {(z_{b}-1)}{2(1+z_{b}}}}}}\qquad \qquad {\text{and}}\qquad z_{\in}=z_{\text}}{\text}}=1}=1}}}}}$

장애물 및 (또는 정상화된 장애물과 )가 순수한 반응인 경우, 네트워크는 평탄한 주파수 응답이지만 가변 위상 응답으로 올패스, 일정한 저항성이 된다.이것은 그들을 지연 네트워크와 위상 평등자로 이상적으로 만든다.

이중성 조건이 여전히 적용되는 경우 저항기가 그 안에 있는 경우 회로는 일정한 저항이지만 가변 진폭 응답을 갖는다.그러한 회로에 대한 한 가지 적용은 진폭 등가속도다.

변환 및 동등성

(참고문헌^[4][6][14] 참조)

T to 격자

파이와 격자 연결

공통열원소자

공통 평행 원소

두 개의 격자를 하나의 격자로 결합

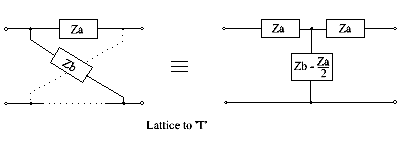
격자와 T 연결(다음 섹션 참조)

이 격자 대 T 변환은 ( Zb- ) / 2의 평가가 양의 값진 구성품을 제공하는 경우에만 실현 가능한 회로를 제공한다.다른 상황의 경우, 다음 절에서 설명한 바와 같이 브리지드-T가 해결책을 제공할 수 있다.

불균형 등가물

격자는 일부 용도에 적합하지 않은 균형 잡힌 구성이다.이러한 경우 회로를 전기적으로 동등한 불균형 형태로 변환해야 한다.이는 구성 요소 수 감소 및 회로 공차를 완화하는 등의 이점을 제공한다.앞의 절에 나타난 간단한 변환 절차는 제한된 조건 집합에서만 적용할 수 있다 – 일반적으로 어떤 형태의 브리지-T 회로가 필요하다.변환의 상당수는 1:1 이상 변압기를 포함시켜야 하지만,^[14] 이러한 요구 조건을 회피하는 몇 가지 구성이 있으며, 아래에 한 가지 예가 나와 있다.

이 변환 절차는 모든 암의 공통 직렬 요소를 격자 바깥으로 두 개의 직렬 요소(위 그림 참조)로 취할 수 있는 격자의 속성을 사용하는 것으로 시작한다.이 성질을 반복적으로 적용하면 격자 구조 내에서 성분을 추출할 수 있다.마지막으로, 바틀렛의 이분법 정리에 의해 불균형한 브리지-T 회로가 달성된다.^[15][16]

왼쪽 그림에서 Za 암에는 션트 캐패시터 C가_a 있고, Zb 암에는 직렬 캐패시터 C가_b 있다.따라서 Za는 Za′과 병렬로 C로_a 구성되며, Zb는 Zb′과 직렬로 C로_b 구성된다.이는 표시된 불균형 브리지-T로 발전할 수 있다, 제공 > .

(이 회로의 대체 버전에는 Pi(또는 델타) 배열로 대체된 캐패시터의 T 구성이 있다.이 T-Pi 변환에 대한 내용은 감쇠기(전자)의 방정식을 참조하십시오.

>일 때, 공통 인덕터를 격자 암에서 먼저 추출하는 대체 절차가 필요하다.그림과 같이 인덕터 L은_a Za′을 션트하고 인덕터 L은_b Zb′과 직렬로 되어 있다.이는 우측의 대체 브리지-T 회로로 이어진다.

> 이 경우, 음의 값 인덕터는 상호 결합된 코일을 사용하여 얻을 수 있다.음의 상호 인덕턴스를 달성하기 위해 결합된 두 인덕터 L1과 L2를 '시리즈 어시딩'으로 감긴다.

마지막으로, 브리지-T 회로가 형태를 취한다.

이와 같은 브리지형-T 회로는 지연 및 위상 교정 네트워크에 사용될 수 있다.

저항기를 포함하는 또 다른 격자 구성은 다음과 같다.왼쪽 그림과 같이 Z를_a 가로지르는 션트 저항기 로와 Z의_b 일부로 시리즈 저항기 로를 가지고 있다.오른쪽과 같이 균형이 맞지 않는 브리지-T 회로로 쉽게 전환된다.

Z₁.Z₂ = ${\displaystyle R}$이₀² 되면 일정한 저항 네트워크가 되어 T($p{\displaystyle }$)${\displaystyle }$= ${\displaystyle R\frac{{}_{}}{}}$ ${\displaystyle \frac{{}_{}}{{}_{}}}$ 0${\displaystyle \frac{{}_{}}{}}$+ Z ${\displaystyle \frac{{1\mathrm{}}_{}p}{}}$) ${\$ {$R_{0}{0}+Z_{1}(p)}}}}}}$에 의해 삽입 손실이 발생하게 된다.

1옴으로 정규화되면 소스와 부하, R이₀ 모두 통일이므로 Z가 된다₁.Z₂ = 1이 되면 삽입 손실은

${\displaystyle T(p)={\frac {1}{{1+Z_{1}(p)}}}$

과거에는 이러한 방식으로 구성된 회로가 진폭 이퀄라이저로 큰 인기를 끌었다.예를 들어, 전화 케이블과^[17] 텔레비전 설치용 동축 케이블의 고주파 손실을 교정하는 데 사용되었다.^[18]

단순 이퀄라이저에 대한 설계 절차를 보여주는 예는 나중에 합성에 관한 섹션에 제시되어 있다.

올패스 네트워크

(앞서 인용한 조벨, 달링턴, 보드, 길레민 참조).스튜어트^[19], 와인버그도 참조)^[1]

올패스 네트워크는 격자망의 중요한 하위 등급이다.그것들은 필터 네트워크와 분산 네트워크의 단계적 보정기로서 수동적인 일괄 요소 지연으로 사용되어 왔다.이들은 지속적인 저항 네트워크로, 불일치 문제를 야기하지 않고 서로와 다른 회로에 계단식으로 연결될 수 있다.

올패스 네트워크의 경우 감쇠 영역이 없으므로 (격자의) 임피던스와 (격자의)는 모든 주파수에서 서로 이중이며 항상 저항성이 있어 와 같다.

즉

${\displaystyle Za\cdot Zb=R_{0}^{2}\qquad \qquad{\text{(모든 주파수에서)}}}$

정규화된 네트워크의 경우, 여기서 = 1은 전송 함수()p를 기록할 수 있다.

${\displaystyle T(p)={\frac {1-z_{a}(p)}{1+z_{a}(p)}}}}}{\frac {z_{b}-1}{z_{b}(p)+1}}}}}}}}$

등등

${\displaystyle z_{a}(p)={\frac {1-T(p)}{1+T(p)}}}{1+T(p)}}}}{1+T(p)}}}}}}}$

실제로()p는 에서 다항식의 비율로 표현할 수 있으며, 또한 다항식의 비율이기도 하다. 장애물이 실현되기 위해서는 포스터의 리액턴스 정리를 만족시켜야 한다.

가장 간단한 두 개의 올패스 네트워크는 제1순서와 제2순서의 선반이다.이것들은 중요한 회로들이다. 왜냐하면,^[20] 보데가 지적했듯이, 모든 고순도 올패스 격자망은 동일한 응답을 주기 위해, 아마도 하나의 1차 주문 네트워크를 가진 2차 주문 네트워크로 계단식으로 대체될 수 있기 때문이다.

이 두 개의 단순하고 정규화된 래티에는 다음과 같은 전달 장애가 있다.

${\displaystyle T_{1}(p)={\frac {-p+c}{p+c}}\qquad \qquad {\text{and}\qquad T_{2}(p)={\p^{p^{2}-ap+b}{p^{p^{2}+b}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}.$

회로는 '합성' 섹션에 자세히 설명되어 있다.

격자 합성

네트워크 합성은 선택된 전송 함수와 일치하는 회로를 도출하는 과정이다.모든 전송 기능이 물리적 네트워크에 의해 실현될 수 있는 것은 아니지만, 가능한 네트워크에 대해서는 격자 네트워크가 항상 해결책이다.즉 대칭적인 2단자 쌍 네트워크가 조금이라도 실현 가능하다면 격자 네트워크로서 실현 가능하다.^{[21]: 39, [20][22]: 339} 이는 격자 구조가 네트워크의 가장 일반적인 형태로서, 예를 들어 T, COLT 또는 브리지-T 네트워크보다 제약조건이 적기 때문이다.

격자 회로가 개발되면 그 결과를 불균형한 형태로 변환하여 접지면이 있는 시스템에서 회로를 사용할 수 있도록 하는 것이 바람직할 때가 많다.^{[20]: 268, [23]: 168 [22]: 352} 또한, 변환 프로세스에서 얻을 수 있는 다른 이점(예: 구성 요소 수 감소 및 구성 요소 허용 오차 감소)이 있다.합성 절차로 인해 몇 가지 가능한 격자 용액이 발생하는 경우, 변환하기 가장 쉬운 용액이 보통 선택된다.흔히 변환과정은 앞에서 보듯이 상호 결합 인덕터를 초래하지만, 높은 삽입 손실 값을 용인할 수 있거나 병렬 ^[24]회로 조합을 고려할 경우 이러한 인덕터를 완전히 피할 수 있는 경우가 있다.^[21]

z 매개변수를 사용한 합성

z-매개변수 또는 임피던스 파라미터는 2포트 네트워크를 정의하는 파라미터 제품군에서 한 세트씩이며,^{[12]: 254 [25]: 29} 그림에서와₁ 같이 I, I₂, V, V에₁₂ 의해 정의된 입력 및 출력 값이다.

네트워크 동작을 z-모수 단위로 정의하는 방정식은

${\displaystyle E_{1}=z_{11}I_{1}+z_{12}I_{2}}:$

${\displaystyle E_{2}=z_{21}I_{1}+z_{22}I_{2}}:$

여기서 z 매개변수는 개방 회로 조건에서 정의되므로(임피던스 매개변수 참조) '개방 회로 매개변수'^[26]라고도 한다.그것들은 다음과^[4] 같이 정의된다.

${\displaystyle z_{11}=\left[{\frac {V_{1}}}}{{1}:{\fracI_{1}}\오른쪽]{\text{{}}{}}}{}}}}}{{}}}}}}{}}}}{{\frac{V_}}}}}}{{}}}}}}{}}}}}}{}}}}}}}{}}}}}}}}}}}}{{}}}}}}}I_{2}}}\오른쪽]{\text{{}{{1}=0} 포함$

${\displaystyle z_{21}=\left[{\frac {V_{2}}:2}}I_{1}}\오른쪽]{\text{{}}{}}}}{}}}}}{}}}}}{}}}}{{\frac{V_}}}}}}}{{}}}}}}}{}}}}}}{}}}}}}}}{}}}}}}}}}}}}}}}}}}}I_{2}}}\오른쪽]{\text{{}{{1}=0} 포함$

대칭 격자의 경우 z-모수 및 격자 임피던스 간의 관계를 쉽게 찾을 수 있으며, 이러한 관계는 다음과 같다.

${\displaystyle z_{11}=z_{22}={\frac {Z_{a}+Z_{b}}}{2}}:\qquad \qquad z_{12}=z_{21}={\frac {Z_{b}-Z_{a}}}}}:{2}}:}}}}}}}}}}}}}}}$

${\displaystyle Z_{I}={\sqrt {Z_{a}Z_{b}}}}}}}}}}}}$

따라서 $Z{\displaystyle {}_{}}$ ${\displaystyle a_{}}$= z ${\displaystyle {11}_{}}$- ${\displaystyle {}_{}}$ ${\displaystyle {12}_{}}$ 및 ${\displaystyle Z_{}}$ ${\displaystyle b{}_{}}$= z ${\displaystyle {11}_{}}$+ z ${\displaystyle {12}_{}}$ ${\$

때때로 격자 합성은 다음 예와 같이 단순히 z의₁₂ 표현 또는 z와₁₁ z의₁₂ 표현 일부를 장애물 Z와_a Z에_b 직접 할당함으로써 달성될 수 있다.

예 1

z가₁₂ 제공될 것으로^{[21]: 229} 간주

${\displaystyle z_{12}={\frac {p^{5}}{{p^{2}+1){{(p^{2}+1)}}}}}}}$

이것은 부분적인 분수로 확장될 수 있다.

${\displaystyle z_{12}={\frac {p}{p^{2}+1}-{\frac {4p}{p^{2}+2}}+p}$

이에 따라 조건을_a Z_b 및 Z에 할당하여 다음을 제공하십시오.

${\displaystyle Z_{a}={\frac {8p}{p^{2}+2}}}$ and ${\displaystyle Z_{b}={\frac {2p}{p^{2}+1}}+2p={\frac {2p^{3}+4p}{p^{2}+1}}}$

Z와_a Z를_b 위한 이러한 솔루션을 가지고 있는 격자망은 아래 왼쪽 회로에 나타나 있다.첫째, 공통 병렬 인덕터를 추출하고, 둘째, 직렬 공통 캐패시터를 추출하여 불균형한 형태로 변환할 수 있다.이것은 우측 회로에 표시된 사다리 네트워크를 제공한다.

개방 회로 전달 함수의 합성

개방₂ 회로 전압-비율 전달 함수 T는 I₁₁ = 0이므로 z 및₁₂ z 단위로 얻을 수 있다.^{[22]: 43}

${\displaystyle T={\frac {V_{2}}:{V_{1}}={\frac {z_{12}}{11}}}}}}}}$

따라서 z와_12, z의₁₁ 비율을 제공하는 T에 대한 식에서_a Z와_b Z에 대한 회로를 얻는 것이 가능할 수 있다.

실제로 T는 형식으로 표현될 수 있다.

${\displaystyle T(p)=K\cdot {\frac {N(p)}{D{p}}}}}$

여기서 N(p)과 D(p)는 p 단위의 다항식이고, 복합 주파수 변수, K는 통일보다 작거나 같은 상수 요인이다.

T에 대해 주어진 식에 대해 K에 대해 선택한 값이 충분히 작다면 식(따라서 Za와 Zb의 회로)을 찾을 수 있는 경우가 많다.

Now, for the lattice, ${\displaystyle T={\frac {z_{11}}{z_{12}}}={\frac {Z_{b}-Z_{a}}{Z_{b}+Z_{a}}}={\frac {1-{\frac {Z_{a}}{Z_{b}}}}{1+{\frac {Z_{a}}{Z_{b}}}}}}$

Z ${\displaystyle \frac{a_{}}{}}$ ${\displaystyle \frac{{}_{}}{{}_{}}}$ ${\displaystyle \frac{b_{}}{}}$= ${\displaystyle 1\frac{\mathrm{}}{}}$- ${\displaystyle \frac{\mathrm{}}{}}$ ${\displaystyle \frac{1}{}}$+ T${\displaystyle \frac{}{}}$= ${\displaystyle D\frac{}{}}$- ${\displaystyle \frac{K}{}}$ ${\displaystyle \frac{}{}}$+ K ${\displaystyle \frac{N}{}}$ ${\$frac $스타일 {\frac$ {$Z_{a}}{b}}={\frac {1-T}{1+T}}={\frac {D-KN}{D$+KN}}}}}}}}}

이 절차는^[24] p의 다항식으로서 표현식의 분자와 분모를 평가한 다음_a Z와_b Z에 대한 부속요소를 평가한다.K < 1을 갖는 손실 조건 K는 실현을 돕기 위해 필요할 수 있다.

예 2

전압^{[22]: 345} 비율 전송 기능 T2로 격자 네트워크를 유도한다.

${\displaystyle T2=K\cdot {\frac {p^{2}+1}{p^{2}+5p+4}}}$

${\displaystyle {\text{with}\quad K=1\qquad D-KN=p^{2}+5.p+4-p^{2}-1=5p+3}$

${\displaystyle {\text{and}\qquad \qquad \qquad D+KN=p^{2}+5p+4+p^{2}+1=2p^{2}+5p+5}$

${\displaystyle {\frac {Z_{a}}{Z_{b}}={\frac {5p+3}{2p^{2}+5p+5}}}}={\frac {1+3/5p}{1+(2p^{2}+5)/5p}}}$

Z${\displaystyle {}_{}}$ ${\displaystyle a_{}}$= ${\displaystyle 1}$+ ${\displaystyle 3\frac{\mathrm{}}{}}$ ${\displaystyle \frac{\mathrm{5p}}{}}$ ${\$ $Z{\displaystyle {}_{}}$ ${\displaystyle b_{}}$= ${\displaystyle 1}$+ ${\displaystyle 2p\frac{\mathrm{}}{}}$ ${\displaystyle \frac{\mathrm{}}{}}$ +${\displaystyle \frac{\mathrm{1p}}{}}$ ${\$}}{$5}}+{\frac{1$}{$p}}}}}}}}}}}}}}}}}}}}}}}$을 선택하십시오.

T2의 격자 실현은 아래 왼쪽과 같다.오른쪽의 불균형 네트워크는 먼저 공통 직렬 저항기를 추출한 다음 캐패시턴스를 추출하여 얻는다.

예 3

L-C 회로에는 다음과 같은 T3 전송 기능이 있다.

${\displaystyle T3=K\cdot {\frac {(p^{4}+1)}{{p^{2}+1)}{{p^{2}+2)}}}}}}}$

K = 0.05로 실현 ^[24]가능하므로

${\displaystyle {\frac {D-KN}{D+KN}={\frac {0.95(p^{4}+3.1579p^{2}+2.0526}{1.05}{1.05}}}{05}}{4}+2.8571p^{2.9524}={\frac {Z_{B}}}}}}}}}}}}}}}}}}}}}}.$

위아래 주기의 인자화

${\displaystyle {\frac {Z_{a}}{Z_{b}}}={\frac {0.95(p^{2}+0.9153)(p^{2}+2.2426)}{11.05(p^{2}+1.1312){2}+1.7259}}}}}}}}}}}}}$

선택하라, 말하라,

${\displaystyle Z_{a}={\frac {0.9048(p^{2}+2.2426)}{{(p^{+}1.1312)}}}}}}}}{\p^{b}={\frac(p+1.7259){p^{2}+0.9153}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

Z와_a Z는_b LC 래더 네트워크로서 실현될 수 있으며, Z는_a 첫 번째 요소로 션트 인덕터를, Z는_b 왼쪽 그림에서와 같이 첫 번째 요소로 직렬 인덕터를 가지고 있다.이 격자는 앞에서 주어진 방법에 의해 불균형한 형태로 변환되어 오른쪽 그림의 성분 값을 제공할 수 있다.

달링턴 합성

달링턴 방법은 규정된 전송 특성에 대한 저항성 종단을 갖는 무손실 두 터미널 쌍 네트워크 합성의 기초를 형성한다.^[27][10]

그림은 기본적인 네트워크 구성을 보여준다.관련 전송 임피던스는

${\displaystyle T={\frac {E_{2}}:{I_{1}:{1}}$

첫 번째 단계는 종료된 네트워크의 입력 임피던스 Z를_I 그것의 z-모수 단위로 표현하는 것이다.이것은

${\displaystyle Z_{I}={\frac {(z_{11}z_{22}-z_{12}^{2})+z_{11}R}{z_{22}+R}}}}}$

여기서 z₁₁, z₂₂ 및 z는₁₂ 앞에서 정의한 것과 같이 네트워크의 z-discuit이다.정규화된 네트워크의 경우 R = 1을 입력하고 식을 다시 정렬하십시오.

${\displaystyle Z_{I}=z_{11}\cdot {\frac {(z_{11}z_{22}z_{12}^{2}}/z_{11}+1}{z_{22}+1}{22}+1}}}}}}}}}}$

실제로 Z는_I p: 2개의 다항식 비율로 구성된다.

${\displaystyle Z_{I}={\frac {N(p)}{D(p)}}}}={\frac {m_{1}+n_{1}={1}={\frac}}}{m_{2}+n_{2}}}}}$

여기서 m과₁ n은₁ 분자 다항식의 짝수와 홀수 부분이고, m과₂ n은₂ 분모 다항식의 짝수와 홀수 부분이다.

${\displaystyle {재배열}_{}}$ Z I${\displaystyle {}_{}}$= ${\displaystyle m\frac{{}_{}}{}}$ 1 ${\displaystyle \frac{{}_{}}{{}_{}}}$ ${\displaystyle \frac{{2\mathrm{}}_{}}{}}$ ${\displaystyle \frac{{}_{}}{}}$ ${\displaystyle (\frac{{}_{}}{}}$ ${\displaystyle \frac{{1\mathrm{}}_{}}{}}$/ m ${\displaystyle \frac{{1\mathrm{}}_{}}{}}$ ${\displaystyle \frac{{}_{}}{}}$+ 1${\displaystyle \frac{}{}}$( ${\displaystyle \frac{{m\mathrm{}}_{}}{}}$ 2${\displaystyle \frac{{}_{}}{}}$/ ${\displaystyle \frac{{n\mathrm{}}_{}}{}}$ 2${\displaystyle \frac{{}_{}}{}}$)${\displaystyle \frac{}{}}$+ ${\displaystyle \frac{1}{}}$ ${\$$I}={\frac {m_{1}:{n_{2}}:\cdot {\frac {(n_{1}/m_{1}}+1}{{{1}}}}{{m_{2}}}}+1}}}}}}}}$

Z에_I 대한 두 식을 비교하여 다음과 같은 관계를 제안한다.

${\displaystyle z_{11}={\frac {m_{1}}{n_{2}}}\qquad \qquad z_{22}={\frac {m_{2}}{n_{2}}}\qquad \qquad z_{12}={\frac {\sqrt {m_{1}m_{2}-n_{1}n_{2}}}{n_{2}}}}$

예 4

다음에_I 의해 제공된 Z를 가진 네트워크 고려

${\displaystyle Z_{I}={\frac {2.1351p^{3}+1.915p^{2}+2.4969p+1}{1.327p^{2}+1.18p+1}}$

${\displaystyle So\qquad \qquad m_{1}=1.915p^{2}+1\qquad \qquad n_{1}=2.1351p^{3}+1}$

$\displaystyle and\qquad \qquad m_{2}=1.327p^{2}+1\qquad \qquad n_{2}=1.18p}$

따라서₁₁ z, z, z를₂₂₁₂ 위한 솔루션은

${\displaystyle z_{11}={\frac {1.915p^{2}+1}{1}.18p}=1.6229p+{\frac {1}{1.18p}}}$

즉, z는₁₁ 1.18F의 콘덴서와 직렬로 1.6229H의 인덕터다.

${\displaystyle z_{22}={\frac {1.327p^{2}+1}{1}.18p}=1.1246p+{\frac {1}{1.18}}$

즉, z는₂₂ 1.1246H의 인덕터와 1.18F의 콘덴서를 직렬로 한다.

${\displaystyle z_{12}={\frac {\sqrt{(1.915p^{2}+1)(1.327p^{2}+1)-(2.13751p^{3}+2.4969p)}{1.18p}}}}}}}$

${\displaystyle \qquad ={\frac {\sqrt {0.0218p^{4}+0.2957p^{2}+1}{1.18p}}}\frac = {0.1479p^{2}+1}{1}{1}18p}\cHB =0.1253p+{\frac {1}{1.18p}}$

z에서₁₁ 0.4983p = (1.6229p – 1.1246p)의 직렬 인덕턴스를 추출함으로써, 나머지 네트워크는 다음과 대칭이 된다.

${\displaystyle z_{11}(신규)=z_{22}=1.1246p+{\frac {1}{1}{1}{1.18p}}\qquad 및\qquad z_{12}=0.1253p+{\frac {1}{1.18p}}}}}}}}}}}$

대칭 격자 성분은 Z_a = z - z₁₂ 및₁₁ Z_b = z + z에서₁₁₁₂ 계산할 수 있다.

So ${\displaystyle Z_{a}=1.1246p+{\frac {1}{1.18p}}-0.1253p-{\frac {1}{1.18p}}=0.9993p}$, i.e. an inductor of 0.9993H.

and ${\displaystyle Z_{b}=1.1246p+{\frac {1}{1.18p}}+0.1253p+{\frac {1}{1.18p}}=1.2499p+{\frac {2}{1.18p}}}$, i.e. an inductor of 1.2499H in series with a capacitor of 0.59F

회로는 아래 왼쪽 그림에 표시되어 있다.그것은 오른손 그림에서 볼 수 있는 불균형한 형태로 쉽게 변환될 수 있다.패스밴드 리플이 1.25dB인 로우패스 필터로 0.169Hz에서는 -3dB, 0.414Hz에서는 정지대역의 null, -40dB 이하의 null 주파수를 초과하는 정지대역 감쇠가 있다.

상수저항 격자망 합성

장애물 Z와_a Z가_b 이중이고 정상화된 경우 다음과 같이 하십시오.

${\displaystyle Z_{a}.Z_{b}=1}$

그러면 영상 임피던스 Z가_I 순수한 저항이 된다.이 조건을 충족하는 대칭 격자는 '항상 저항 격자'이다.

1옴으로 종료된 이러한 격자는 다음과 같다.

이것은 전달 기능을 가지고 있다.

${\displaystyle {\frac {E_{2}}:{E_{1}}={\frac {E_{2}}:}{{\frac}}{{2}}:{I_{1}}=T={\frac{1-Z_{a}}{1+Z_{a}}}}}}$

여기서 T는 개방 회로 전송 임피던스 z와₂₁ 대조적으로 1옴 로드의 전송 임피던스다.이것을 재정비하면,

${\displaystyle Z_{a}={\frac {1-T}{1+T}}}$

따라서 일정한 저항 격자는 전달 함수의 합성에 대한 가능한 접근방식을 제공하는 것으로 간주된다.

상수 저항 격자가 다른 격자보다 일반적이지 않은 경우로서, 실현 가능한 전송 임피던스는 상수 저항 격자 형태로 실현될 수 있다.^{[20]: 233 [21]: 480} 이러한 네트워크는 구간 간 또는 저항성 종단과의 불일치가 없기 때문에 매우 편리하다.따라서 연속 저항 섹션의 계단식 삽입 손실은 개별 섹션의 합계를 단순히 합한 것이다.반대로, 주어진 복잡한 전송 임피던스는 승법 인자로 분해될 수 있다. 이 인자의 개별 격자 실현은 계단식으로 연결되었을 때, 그 전송 임피던스의 합성을 나타낸다.따라서 복잡한 임피던스 Z와_a Z를_b 가진 단일 격자를 합성하는 것은 가능하지만, 실제로는 더 단순한 회로의 계단식 구성과 정렬이 더 쉽다.

올패스 상시 저항 네트워크

올패스 네트워크는 주파수에 따라 일정한 이득이 있지만, 어떤 식으로든 변화하는 위상 응답을 가지고 있다.예를 들어 격자 지연 네트워크의 경우, 위상 반응은 지정된 주파수 범위에 걸쳐 주파수로 선형인 반면, 격자 위상 이퀄라이저의 경우 네트워크의 위상 반응이 필터 네트워크의 비선형 위상 응답을 보상하기 위해 이탈한다.

1차 및 2차 주문 네트워크가 가장 중요한^{[20]: 240} 이유는 보데가 지적한 바와 같이, 이러한 네트워크들은 복잡한 고주문 격자와 동일한 결과를 주기 위해 필요에 따라 계단식으로 배치될 수 있기 때문이다.

예 5

첫 번째 주문의 올패스 응답은

${\displaystyle T5={\frac {c-p}{c+p}}}$

이것은 +c에 0이 위치하며 복잡한 주파수 평면에서 –c에 극이 위치한다.주파수에 따라 위상이 달라지는 반응이 있지만 T5의 크기는 모든 주파수에서 통일이다.

Z에_a 대한 식을 T의 함수로 사용하는 것은, 앞에서부터,

${\displaystyle Z_{a}={\frac {1-T5}{1+T5}={\frac {p}{c}}}}$

따라서 Z는_a 값 1/c를 가진 인덕턴스로서, 결과적으로 Z는_b 값 1/c의 커패시터다.1옴으로 정규화된 네트워크는 아래 왼쪽 그림에 표시된다.

예 6

두 번째 순서의 올패스 응답은

${\displaystyle T6={\frac {p^{2}-ap+b}{p^{2}+ap+b}}}}$

여기에는 $x{\displaystyle }$± ${\displaystyle y}$ ${\displaystyle x\pm y}$에 두 개의 ${\displaystyle 0}$이 있고$$ -${\displaystyle }$x${\displaystyle }$± ${\displaystyle y}$ ${\displaystyle -x\pm y}$에 두 개의 극이 있으며, 여기서 a = 2x 및 b = x² + y이다².그러한 반응의 경우 주파수에 따라 위상이 달라지지만 T6의 크기는 모든 주파수에서 통일이다.

이러한 특성에 대해 Z는_a 다음에서 찾을 수 있다.

${\displaystyle Z_{a}={\frac {1-T6}{1+T6}}={\frac {ap}{p^{2}+b}}}}}}}$

따라서 Z는_a 캐패시턴스 1/a와 값이 a/b인 인덕턴스의 병렬 조합이다.마찬가지로 Z는_b 값 a/b의 콘덴서와 직렬로 인덕터 1/a이며 네트워크는 아래 오른쪽에 표시된다.

격자 네트워크는 앞에서 나타낸_a Z와_b Z, 그리고 바틀렛의 바이섹션 정리에서 모두 공통 원소가 있는 격자의 특성을 이용하여 불균형 회로로 변환할 수 있다.^{[16]: 28}

2차 순서 네트워크의 경우, a2 > b(예: L1 > L2 또는 C2 > C1 또는 y > √3x)의 경우, 2차 순서 올패스 네트워크에는 상호 결합 코일이 포함된 회로를 사용할 필요가 있다.

아마도 단일 1차 주문 네트워크가 있는 2차 주문 네트워크의 계단식 네트워크를 사용하여 높은 주문 응답을 제공할 수 있다.예를 들어, Lattice 지연 네트워크 기사에서는 선형 위상 특성에 근접한 많은 올패스 전송 기능에 대해 극 영점 위치를 제공한다.그 글에는 몇 가지 사례도 포함되어 있다.

진폭 이퀄라이저 합성

일반적인 전송 경로는 주파수와 함께 손실이 증가하며 이는 주파수와 함께 상승하는 응답성을 가진 평준화 네트워크로 시스템을 계단식으로 배치하여 수정할 수 있다.이와 관련하여 필요한 등화 기능을 제공하기 위해 일반적으로 사용되는 회로 구성은 앞에서 설명한 그림('비균형 등가물' 섹션)에 '격자 - 기본 등가물 회로'로 표시되어 있다.As stated there, the insertion loss of the normalized circuit is given by ${\displaystyle T={\frac {1}{1+Z_{1}(p)}}}$, so Z₁ can be found from ${\displaystyle Z_{1}(p)={\frac {1}{T(p)}}-1}$

응답에 대한 잔존 리플이 허용될 경우 Z와₁₂ Z에는 단순 보정 네트워크로 충분하지만, 보다 복잡한 보정 네트워크를 채택하여 원하는 만큼 이 리플을 줄일 수 있다.Z와₁ Z에₂ 대한 극과 0의 위치를 선택하는 것은 직선의 점근법일 수 있다.^[28]

예 7

제한된 주파수 범위에 걸쳐 상승 반응을 갖는 전송 기능은

${\displaystyle T7(p)={\frac {3.333+10.333p+p^{2}}{30.003+31.003p+p^{2}}}}={\frac {(0.3333+p)(10+p)}{(1+p)(30.003+p)}}}$

응답은 높은 주파수에서 단일화에 접근한다는 점에 유의하십시오.Z가₁ R-C 네트워크인 브리지-T 또는 격자로 실현될 수 있다.

Z₁ can be found from ${\displaystyle Z_{1}(p)={\frac {1}{T(p)}}-1}$. So ${\displaystyle Z_{1}(p)={\frac {26.6697+20.6697p}{3.3333+10.3333p+p^{2$$}}}}$

입장₁₁ Y, 여기서₁ Y = 1/Z는 4개의 항을 포함하는 연속 분수로 표현될 수 있으므로

${\displaystyle Y_{1}(p)={\frac {p^{2}+10.333p+3.3333}{20.6697p+26.6697}}=0.04838+{\cfrac {1}{2.2857+{\cfrac {1}{0.4747p+{\cfrac {1}{5.7153}}}}}}}$

그래서 Z는₁ R-C 사다리 네트워크, 카우어 방식으로 실현될 수 있으며,^[21] 아래 브리지-T 회로의 일부로 보여진다.Z는₂ Z의₁ 이중형이며, R-L 회로도 그림과 같다.등가 격자 회로가 우측에 표시된다.

상시 저항 저역 통과 필터

고차 저역 통과 필터는 적절한 수의 단순 상수 저항 저역 통과 섹션을 계단식으로 배치하여 얻을 수 있다.^{[21]: 484}

이러한 저역 통과 구간 중 첫 번째 구간은 단 하나의 극으로 응답한다.

${\displaystyle T_{1}={\frac {k_{1}:{p+a}\qquad so\qquad Z_{a1}={\frac {1-T_{1}:{1}:{1+}T_{1}}={\frac {p+(a-k_{1}}}}{p+(a+k_{1}})}}}$

$k{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle a}$ ${\displaystyle k_{1}\leq a}$이(가) 제공될 경우 이는 실현 가능한 임피던스인데, 여기서_a1 Z는 아래의 좌측 회로와 같이 두 저항기와 인덕터의 조합이며, Z는_b1 Z의_a1 이중이다.이것은 오른쪽에 보이는 것처럼 쉽게 불균형한 형태로 변형된다.

두 개의 극이 있는 두 번째 필터 섹션의 응답은

${\displaystyle T_{2}=k_{2}.{\frac {(p+a)}{(p^{2}+b_{1}p+b_{0}}}}}}}}$

그래서 격자 임피던스 Za2는 다음과 같이 주어진다.

${\displaystyle Z_{a2}={\frac {p^{2}+(b_{1}-k_{2})p+(b_{0}-a).k_{2}}{p^{2}+(b_{1}+k_{2})p+(b_{0}+a)k_{2}}}}}$

이것이 실현 가능한 네트워크라는 것을 확실히 하기 위해서는 일정한 조건이 충족되어야 하는데,^{[21]: 486} 그 네트워크는 다음과 같다.

${\$$\qquad }$ 또한$$ ${\displaystyle {b\mathrm{}}_{}}$ 1${\displaystyle {}_{}}$- ${\displaystyle {k\mathrm{}}_{}}$ ${\displaystyle {}_{}o}$ ${\displaystyle r}$ k ${\displaystyle {2\mathrm{}}_{}}$≤ ${\displaystyle {b\mathrm{}}_{}}$ ${\displaystyle {}_{}}$- ${\displaystyle a}$ ${\displaystyle b_{1}-k_{2}\geq a\qquad k_{2}\leq b_{1}-a}$.

조건은 T에₂ 대한 식에서 상수 승수 k의₂ 값에 대한 한계를 설정한다.

격자 요소 Z에_a2 대한 회로는 왼쪽, 아래, 이중 요소_b Z에 대한 회로는 오른쪽에 표시된다.

자를 구성 요소 값, R1)b1− k2− 2k2L=12k2C=2k2b0− b1+a2는 2k2R2)b0− b1+a2는 2k− 2{\displaystyle R_{1}={\frac{b_{1}-k_{2}-a}{2k_{2}}}\qquad L={\frac{1}{2k_{2}}}\qquad C={\frac{2k_{2}}{b_{0}-ab_{1.}$+a^{2}}:{2ak_{2}}\\qquad R_{2}={\frac {b_{0}-ab_{1}+a^{2$$}={\frac {b_{0}-ab_{1}+a^{2}$$2}}:{2ak-2}}:}$

and those for the impedances Z_b2 are: ${\displaystyle R_{3}={\frac {1}{R_{1}}}\qquad R_{4}={\frac {1}{R_{2}}}\qquad C_{2}=L_{1}\quad and\quad L_{2}+C_{1}}$

이 격자의 불균형 버전은 다음과 같다.

방금 개발된 유형의 여러 1차 및 2차 순서의 회로를 계단식으로 배열함으로써 다음과 같은 유형의 고차 저역 통과 네트워크를 도출할 수 있다.

${\displaystyle T_{n}(p)={\frac {k}{p^{n}+b_{n-1}p^{n-1}p^{n-1}p^{n-1}+\cdots +b_{2}p^{2}+b_{1}p+b_{0}}}}$

그렇게 얻은 격자망은 k의 값이 충분히 작다면 불균형한 형태로 변환될 수 있다.

예 8

최대 평탄한 3차 표준화된 로우패스 필터에는 전송 기능이 있다.

${\displaystyle T8={\frac {k}{p^{3}+2p^{2}+2p+1}}}$

이는 다음과 같이 확장할 수 있다.

${\displaystyle T8={\frac {k_{1}{p+a}\times {\frac {k_{2}(p+a)}{p^{2}+p+1}}}\time {\frac {1}{p+1}}}}}}}$

그래서 3개의 격자무늬가 필요한 결과를 줄 것이다.

균형이 맞지 않는 회로가 필요하다면 전체적인 손실을 감수해야 한다.k₁ = k₂ = a = 0.5를 선택하면 아래와 같은 네트워크를 얻을 수 있다.이 회로는 전체적으로 4배의 손실이 있는 반면, 기존의 L-C 사다리 네트워크는^{[1]: 605} 손실이 없다(그러나 상수저항 네트워크는 아니다).

컴퓨터 지원 설계 방법

20세기 마지막 분기에 메인프레임과 그 후 개인용 컴퓨터의 개발은 수치 처리 기술의 급속한 발전을 가능하게 했다.초기에는 컴퓨터가 네트워크 분석의^[29] 보조 수단으로 사용되었고,^[30] 그 후 위상 이퀄라이저와^[31] 필터^[32] 설계에서 미니맥스 방법과 같은 최적화 방법을 네트워크 통합에 직접 적용하였다.합성 분야의 소프트웨어 개발에 대한 개요는 테일러&황과^[33] 궈에서 제공되었다.^{[12]: 438}

초기 합성 프로그램들 중 몇몇만이 격자망을 다루었지만, S-Filsyn (강력한 합성 및 분석 프로그램^[34])은 격자와 브리지-T 회로의 일부 커버리지를 제공한다.

초기 역사

대칭 격자망과 사다리망(상수 k 필터와 m 유래 필터)^{[4][7][35][36]}은 20세기 초반에 많은 관심을 끌었다.당시 급속히 성장하는 전화 산업은 전화 송수신 라인의 신호 전달 능력을 높이는 동시에 필터 이론의 발전에 큰 영향을 끼쳤다.^[37]George Ashley Campbell은 오토 줄리어스 조벨과 마찬가지로 이 새로운 필터 이론의 핵심 공헌자였다.이들과 많은 동료들은 웨스턴 일렉트릭과 아메리칸 텔레그래프사의 연구소에서 일했으며,^[37] 이들의 작업은 벨 시스템 테크니컬 저널(Bell System Technical Journal)의 초판에 보고되었다.

캠벨은 1922년 기고문에서 격자 필터에 대해 논의했고,^[7] 격자에 관심이 있는 다른 초기 근로자들은 존슨과^[38] 바틀렛을 포함했다.^[39]이 무렵에 ^[35]출판된 조벨의 필터 이론과 디자인에 관한 기사는 래더 네트워크를 주로 강조하면서 격자만 간단히 언급했다.조벨이 전화 송수신 회선의 시뮬레이션과 평준화를 고려했을 때 비로소 격자 구성에 더욱 주의를 기울였다.^[40](당시의 전화 송신선은 600옴의 공칭 특성 임피던스를 가진 균형 쌍 구성을 가지고 있었기 때문에,^[41] 균형 잡힌 구조를 가진 격자 이퀄라이저는 특히 그들과 함께 사용하기에 적합했다.)이후 작업자들, 특히 헨드릭 웨이드 보드는 필터 설계에서 격자망에 더 큰 중요성을 부여했다.^[20][36]

그 초기에는, 필터 이론은 이미지 임피던스 개념, 즉 이미지 필터 이론에 근거하고 있었는데, 이것은 전송 라인의 잘 확립된 연구로부터 개발된 설계 접근법이었다.필터는 송전선 한 구간의 구성부품 덩어리 버전으로 간주되었으며, 유사한 구간의 계단식 내 다수 중 하나였다.위에서 언급한 바와 같이, 이미지 필터 접근법의 약점은 네트워크의 주파수 응답이 필요한 이미지 임피던스에 의해서가 아니라, 네트워크가 저항적으로 종료되었을 때 예측되지 않는 경우가 많다는 것이었다.이것은 본질적으로 불일치 문제였고 조벨은 끝부분을 일치시키는 방법으로 그것을 극복했다.(m- 파생 필터, mm'-type 필터, General mn-type 이미지 필터, 이후 Payne^[42] 및 Bode 작업 참조)^[43]

격자 필터는 때때로 이와 같은 문제를 겪지만, 다양한 내성 네트워크는 이를 완전히 피할 수 있다.

1930년대에는 네트워크 분석과 합성의 기술이 발전하면서 이미지 방법에 의한 래더 필터 설계는 인기가 떨어졌다.그럼에도 불구하고, 그 개념들은 일부 현대적인 디자인에서 여전히 관련성을 발견하였다.^[44]반면에 격자망과 그 회로 등가물은 많은 애플리케이션에서 계속 사용된다.

참고 항목

• 격자 위상 이퀄라이저
• 올패스 필터
• 2포트 네트워크
• 합성 이미지 필터
• 격자 지연 네트워크
• 사다리 네트워크

참조