최장공통부현

컴퓨터 과학에서 두 개 이상의 문자열로 이루어진 가장 긴 공통 부분 문자열은 모든 문자열의 하위 문자열인 가장 긴 문자열입니다. 하나 이상의 긴 공통 부분 문자열이 있을 수 있습니다. 응용 프로그램에는 데이터 중복 제거 및 표절 검사가 포함됩니다.

예

그림은 문제가 여러 해결책을 가지고 있는 두 개의 문자열을 보여줍니다. 서브스트링이 항상 겹치지만, 이들을 "통합"하여 더 긴 공통 서브스트링을 얻는 것은 불가능합니다.

문자열 "ABABC", "BABCA" 및 "ABCB"A"는 하나의 가장 긴 공통 부분 문자열인 viz만 있습니다. 길이 3의 "ABC". 다른 일반적인 기판으로는 "A", "AB", "B", "BA", "BC" 및 "C"가 있습니다.

  ABC BABCA ABCBA

문제정의

Given two strings, $S$ of length $m$ and $T$ of length $n$ , find a longest string which is substring of both $S$ and $T$ .

일반화는 k-공통 서브스트링 문제입니다. Given the set of strings $S=\{S_{1},\ldots ,S_{K}\}$ , where $S_{i} =n_{i}$ and ${\textstyle \sum n_{i}=N}$ . Find for each $2\leq k\leq K$ , $k개$ 이상의 $k$ 문자열의 $k$ 하위 문자열로 발생하는 가장 긴 문자열입니다.

알고리즘

일반화된 접미사 트리를 통해 $\Theta$ θ ${\displaystyle$ \ $(n+m)$ n $(n+m)$ + m) ${\displaystyle ($ n + m) {\displaystyle (n + m)} $S$ 에서 S $S$ $T$ T ${\displaystyle$ T $}$ 의 가장 긴 공통 기판의 길이 및 시작 위치를 확인할 수 있습니다. 입력 $2^{o\left({\sqrt {\log(n+m)}}\right)}$ 의 크기 $\sigma$ σ ${\$ displaystyle $\sigma$ \sigma}가 $2^{o\left({\sqrt {\log(n+m)}}\right)}$ ⁡(n + m ) ${\displaystyle 2^{o\left({\sqrt$ {\log $($ n $2^{o\left({\sqrt {\log(n+m)}}\right)}$ m))}}\right)}}인 경우 계산의 워드 RAM 모델에서 더 빠른 알고리즘을 얻을 수 있습니다. 특히, $이$ 알고리즘은 O ${\textstyle O\left((n+m)\log \sigma /{\sqrt {\log(n+m)}}\right)}$ + ${\textstyle O\left((n+m)\log \sigma /{\sqrt {\log(n+m)}}\right)}$ ) ${\textstyle O\left((n+m)\log \sigma /{\sqrt {\log(n+m)}}\right)}$ ⁡ σ ${\textstyle O\left((n+m)\log \sigma /{\sqrt {\log(n+m)}}\right)}$ / ${\textstyle O\left((n+m)\log \sigma /{\sqrt {\log(n+m)}}\right)}$ $O\left((n+m)\log \sigma /\log(n+m)\right)$ ${\textstyle O\left((n+m)\log \sigma /{\sqrt {\log(n+m)}}\right)}$ ⁡ (n + m ) ${\textstyle O\$ left((n + m))\log \sigma / {\sqrt {\log(n + m))}\right}} 시간에서 O( (n + m ) log ⁡ σ / log ⁡ (n + m ) {\displaystyle O\left((n + m))\log \sigma /\log(n + m )\right)} 공간을 사용하여 실행됩니다. 동적 프로그래밍으로 문제를 해결하는 데는 $\Theta (nm)$ θ(nm) ${\displaystyle$ \Theta(nm)}이 듭니다. The solutions to the generalized problem take $\Theta (n_{1}+\cdots +n_{K})$ space and $\Theta (n_{1}\cdots n_{K})$ time with dynamic programming and take ${\displaystyle \Theta ((n_{1}+\cdots +n_{K})\cdot$ $K)$ 일반화된 접미사 트리가 있는 $\Theta ((n_{1}+\cdots +n_{K})\cdot K)$ } 시간입니다.

접미사 트리

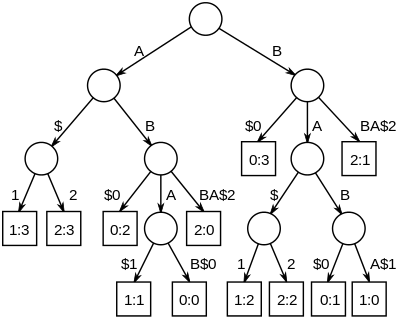
문자열 집합의 가장 긴 공통 서브스트링은 문자열에 대한 일반화된 접미사 트리를 구축한 다음 그 아래 하위 트리에 있는 모든 문자열의 리프 노드가 있는 가장 깊은 내부 노드를 찾는 것으로 찾을 수 있습니다. 오른쪽 그림은 문자열 "ABAB", "BABA" 및 "ABBA"의 접미사 트리로, 고유 문자열 종결자가 패딩되어 "ABAB$0", "BABA$1" 및 "ABBA$2"가 됩니다. "A", "B", "AB" 및 "BA"를 나타내는 노드는 모두 번호 0, 1 및 2인 모든 문자열에서 파생된 잎을 가지고 있습니다.

접미사 트리를 작성하는 데는 $\Theta (N)$ θ(N) ${\displaystyle \$ Theta(N)} 시간이 걸립니다(알파벳의 크기가 일정한 경우). 각 노드 아래에 어떤 문자열이 있는지 알려주는 비트 벡터로 트리를 아래에서 위로 횡단하면 k-공통 부분 문자열 문제를 $\Theta (NK)$ θ $($ NK) ${\displaystyle \Theta$ (NK)} 시간에 해결할 수 있습니다. 접미사 트리가 일정한 시간 최저 공통 조상 검색을 위해 준비되면 $\Theta (N)$ θ(N) ${\displaystyle \Theta($ N)} 시간 내에 해결할 수 있습니다.

동적 프로그래밍

다음 의사 코드는 동적 프로그래밍이 있는 두 문자열 사이에서 가장 긴 공통 서브스트링 집합을 찾습니다.

함수 LongestCommonSubstring(S[1..r], T[1..n]) L := array(1..r, 1..n) z := i : = 1..r인 경우 i : = 1..r인 경우 S[i] = 1..n인 경우 T[j] = 1 L[i, j] : = 1 다른 L[i, j] : = L[i - 1, j - 1] + 1인 경우 j] > z z : = L[i, j] ret : = {S[i - z + 1..i]L[i,j] = zret := ret ∪ {S[i - z + 1..i]} 이외의 L[i, j] := 0 반환 리트

이 알고리즘은 $O(nr)$ $O(nr)$ 시간 $O(nr)$ 내에 실행됩니다. 배열이 L 접두사 중 가장 긴 공통 부분 문자열의 길이를 저장합니다. S[1..i] 그리고. T[1..j] 위치에서 끝나는 i 그리고. j,각각 다음과 같다. 변수가 z 지금까지 발견된 가장 긴 공통 하위 문자열의 길이를 고정하는 데 사용됩니다. 세트가. ret 길이가 긴 문자열 집합을 고정하는 데 사용됩니다. z. 세트가. ret 인덱스만 저장하면 효율적으로 저장할 수 있습니다. i, 대신 가장 긴 공통 부분 문자열(크기 z)의 마지막 문자입니다. S[i-z+1..i]. 따라서 가장 긴 일반적인 기판은 각각의 i에 대해 ret, S[(ret[i]-z)..(ret[i])].

구현의 메모리 사용량을 줄이기 위해 다음과 같은 방법을 사용할 수 있습니다.

메모리를 저장하려면 DP 테이블의 마지막 행과 현재 행만 유지합니다( $O(nr)$ ${\display O(nr)}$ 대신 $O(\min(r,n))$ ${\min(r, n$ {\ $display O($ r, n $O(nr)$
- 내부 루프를 역방향으로 횡단하여 마지막 행과 현재 행을 동일한 1D 배열에 저장할 수 있습니다.
0이 아닌 값만 행에 저장합니다. 어레이 대신 해시 테이블을 사용하여 수행할 수 있습니다. 이것은 큰 알파벳에 유용합니다.

참고 항목

가장 긴 회문 하부끈
n그램, 문자열에 포함된 길이 n의 가능한 모든 부제

참고문헌

^ Charalampopoulos, Panagiotis; Kociumaka, Tomasz; Pissis, Solon P.; Radoszewski, Jakub (Aug 2021). Mutzel, Petra; Pagh, Rasmus; Herman, Grzegorz (eds.). Faster Algorithms for Longest Common Substring. European Symposium on Algorithms. Leibniz International Proceedings in Informatics (LIPIcs). Vol. 204. Schloss Dagstuhl. doi:10.4230/LIPIcs.ESA.2021.30. 여기: 정리 1, 페이지 30:2.
^ Gusfield, Dan (1999) [1997]. Algorithms on Strings, Trees and Sequences: Computer Science and Computational Biology. USA: Cambridge University Press. ISBN 0-521-58519-8.

외부 링크

[CKPR21-1] Charalampopoulos, Panagiotis; Kociumaka, Tomasz; Pissis, Solon P.; Radoszewski, Jakub (Aug 2021). Mutzel, Petra; Pagh, Rasmus; Herman, Grzegorz (eds.). Faster Algorithms for Longest Common Substring. European Symposium on Algorithms. Leibniz International Proceedings in Informatics (LIPIcs). Vol. 204. Schloss Dagstuhl. doi:10.4230/LIPIcs.ESA.2021.30. 여기: 정리 1, 페이지 30:2.

[Gus97-2] Gusfield, Dan (1999) [1997]. Algorithms on Strings, Trees and Sequences: Computer Science and Computational Biology. USA: Cambridge University Press. ISBN 0-521-58519-8.

v t 줄들
문자열 메트릭	대략적인 문자열 일치 비트맵 알고리즘 다메로-레벤슈테인 거리 거리 편집 게스탈트 패턴 매칭 해밍 거리 자로-윙클러 거리 리 거리 레벤슈테인 오토마톤 레벤슈테인 거리 바그너-피셔 알고리즘
문자열 검색 알고리즘	사도-지안카를로 알고리즘 보이어-모어 문자열 검색 알고리즘 보이어-무어-호스풀 알고리즘 크누스-모리스-프라트 알고리즘 라빈-카르프 알고리즘 라이타 알고리즘 트리그램 검색 양방향 문자열 일치 알고리즘 Zhu-Takaoka 문자열 일치 알고리즘
다중 문자열 검색	Aho–Corasick Commentz-Walter 알고리즘
정규식	정규 표현식 엔진의 비교 정규문법 톰슨의 작법 비결정론적 유한 오토마톤
순서 정렬	폭발. 허쉬버그의 알고리즘 니들맨 –운슈 알고리즘 스미스-워터맨 알고리즘
자료구조	DAFSA 접미사 배열 접미사 오토마톤 접미사 트리 일반화된 접미사 트리 출렁 삼원검색트리 트리
다른.	구문 분석 패턴매칭 압축패턴매칭 최장공통후계 최장공통부현 순차 패턴 마이닝 정렬 문자열 재작성 시스템 문자열 연산

Search