PID 컨트롤러
PID controller비례-통합-파생 제어기(PID 제어기 또는 3기 제어기)는 산업 제어 시스템 및 연속적으로 변조된 제어가 필요한 다양한 애플리케이션에서 널리 사용되는 피드백을 사용하는 제어 루프 메커니즘이다.PID 컨트롤러는 원하는 설정점(SP)과 측정 프로세스 변수(PV)의 차이로서 e를 연속적으로 산출하여 비례항, 적분항 및 파생항(각각 P, I, D)에 근거해 보정을 실시한다.
실용적인 측면에서 PID는 자동으로 제어 기능에 정확하고 응답성 있는 보정을 적용합니다.일상적인 예로는 자동차의 크루즈 컨트롤이 있는데, 일정한 엔진 출력을 적용하면 언덕을 오르면 속도가 느려집니다.컨트롤러의 PID 알고리즘은 엔진의 출력을 제어 방식으로 증가시킴으로써 측정된 속도를 최소 지연 및 오버슈트로 원하는 속도로 복원합니다.
PID의 첫 번째 이론적 분석과 실용적 적용은 1920년대 초부터 개발된 선박용 자동 조향 시스템 분야였다.제조업계에서 자동 공정 제어에 사용되었으며, 처음에는 공압식 컨트롤러에서 그 다음에는 전자 컨트롤러에서 광범위하게 구현되었습니다.오늘날 PID 개념은 정확하고 최적화된 자동 제어가 필요한 애플리케이션에서 보편적으로 사용됩니다.
기본 조작

PID 컨트롤러의 구별되는 기능은 컨트롤러 출력에 대한 비례, 적분 및 파생 영향의 세 가지 제어 용어를 사용하여 정확하고 최적의 제어를 적용할 수 있다는 것입니다.오른쪽 블록 다이어그램은 이러한 용어가 생성되고 적용되는 원리를 보여 줍니다.이 화면에는 PID 컨트롤러가 표시되어 있습니다. 이 컨트롤러는 e () { e을(를 원하는 SP ( t) { {text 사이의 차이로 연속적으로 계산합니다. 및 측정된 공정 PV ( ) \ { :e () () - ( e)=이며, 비례항, 적분항 및 미분항에 따라 보정을 적용한다.컨트롤러는 컨트롤 밸브의 개방과 같은 변수( t {(t을(를) 컨트롤 용어의 가중치 합계에 의해 결정되는 새로운 값으로 조정하여 시간 경과에 따른 오류를 최소화하려고 합니다.
이 모델에서는:
- 용어 P는 SP - PV e ( ) {displaystyle e의 현재 값에 비례합니다. 예를 들어 오류가 클 경우 게인 계수 "Kp"를 사용하여 제어 출력이 비례적으로 커집니다.컨트롤러가 비례 출력 응답을 생성하는 데 오류가 필요하므로 비례 제어만 사용하면 설정 지점과 공정 값 사이에 오류가 발생합니다.정상 상태 프로세스 조건에서는 안정된 SP-PV "오프셋"으로 평형에 도달합니다.
- 항 I은 SP - PV 오류의 과거 값을 설명하고 시간 경과에 따라 이를 통합하여 항 I을 생성합니다.예를 들어, 비례 제어를 적용한 후에 잔류 SP - PV 오차가 있는 경우, 적분 항은 오차의 과거 누적 값으로 인한 제어 효과를 추가하여 잔류 오차를 제거하려고 합니다.오류가 제거되면 적분항은 더 이상 증가하지 않습니다.이는 오차가 감소함에 따라 비례 효과가 감소하지만, 이는 증가하는 적분 효과로 보상됩니다.
- 용어 D는 SP - PV 오류의 현재 변화율에 기초한 미래 추세에 대한 최선의 추정치입니다.오류 변화율에 의해 생성된 제어 영향력을 행사함으로써 SP - PV 오류의 영향을 효과적으로 감소시키기 위해 "예측 제어"라고 부르기도 한다.변화가 빠를수록 제어 또는 댐핑 효과가 [1]커집니다.
튜닝 – 이러한 효과의 균형은 최적의 제어 기능을 생성하기 위한 루프 튜닝에 의해 달성됩니다.튜닝 상수는 아래에 "K"로 나타나 있으며 컨트롤러 외부 전체 루프의 응답 특성에 따라 달라지기 때문에 각 제어 애플리케이션에 대해 도출되어야 합니다.이는 측정 센서, 최종 제어 요소(예: 제어 밸브), 제어 신호 지연 및 프로세스 자체의 동작에 따라 달라집니다.일반적으로 상수의 대략적인 값은 처음에는 적용 유형을 알고 입력할 수 있지만, 일반적으로 설정점 변경을 도입하고 시스템 응답을 관찰함으로써 실제 프로세스를 "범핑"함으로써 미세화되거나 조정됩니다.
제어 작용 – 위의 수학적 모델과 실제 루프 모두 모든 항에 대해 직접 제어 작용을 사용합니다. 즉, 양의 오차가 증가하면 양의 제어 출력 보정이 증가합니다.부정적인 시정 조치를 적용해야 할 경우 이 시스템을 역작용이라고 합니다.예를 들어 플로우 루프 내의 밸브가 0~100%의 제어 출력에 대해 100~0%의 밸브 개방 상태일 경우 컨트롤러의 동작을 반대로 해야 합니다.일부 프로세스 제어 체계 및 최종 제어 요소에서는 이 역처리가 필요합니다.예를 들어 냉각수용 밸브를 들 수 있는데, 신호 손실 시 페일 세이프 모드는 밸브의 100% 개방이므로 0% 컨트롤러 출력은 100% 밸브 개방이 필요합니다.
수학적 형식
전체 제어 ( ) K () + i t ( ) + ( ) t,\ u ( t ) = { \} \ { ) \ \ displaystyle ( t )
서 Kp {\ K_ {\{i K {\는 모두 음이 아닌 값으로, 각각 비례, 적분 및 미분 항의 계수(P, I, D로 표시되기도 함)를 나타냅니다.
이 방정식의 표준 형식(기사의 후반 참조)에서 와 는 각각 K_text로 T_는 각각 적분시간과 파생시간을 나타내므로 물리적인 의미를 장점이 있습니다.은(는) 컨트롤러가 설정 지점에 접근을 시도하는 시간 상수입니다.p / { K _ { \ { } } / T _ { \ { } 、컨트롤러가 출력을 설정값 이상 또는 이하로 일정하게 허용하는 시간을 결정합니다.
관리 용어의 선택적 사용
PID 컨트롤러에는 3개의 제어 용어가 있지만 일부 응용 프로그램에서는 적절한 제어를 제공하기 위해 1개 또는 2개의 용어가 필요합니다.이는 사용되지 않는 파라미터를 0으로 설정함으로써 실현되며, 다른 제어 액션이 없을 경우 PI, PD, P 또는 I 컨트롤러라고 불립니다.PI 컨트롤러는 파생 작용이 측정 노이즈에 민감할 수 있는 애플리케이션에서 매우 일반적이지만 시스템이 목표값에 도달하기 위해 종종 필수 용어가 필요합니다.
적용 가능성
PID 알고리즘을 사용해도 시스템의 최적 제어 또는 제어 안정성이 보장되지 않습니다. 의 을 참조).프로세스 값의 측정이 지연되거나 제어 액션이 충분히 신속하게 적용되지 않는 등 과도한 지연이 발생하는 경우가 있습니다.이 경우 납-지연 보상은 유효해야 한다.컨트롤러의 응답은 오류에 대한 응답성, 시스템이 설정값을 오버슈팅하는 정도 및 시스템 진동 정도에 따라 설명할 수 있습니다.그러나 PID 컨트롤러는 기초 프로세스의 지식이나 모델이 아닌 측정된 프로세스 변수의 응답에만 의존하기 때문에 광범위하게 적용할 수 있습니다.
역사

오리진스
PID 컨트롤러가 완전히 이해되고 구현되기 전의 연속 제어는 회전 중량을 사용하여 프로세스를 제어하는 원심 조속기에서 비롯되었습니다.이는 17세기 크리스티안 호이겐스가 풍차의 맷돌 간격을 회전 속도에 따라 조절해 곡물의 [2][3]공급 속도를 조절하기 위해 고안했다.
저압 정지 증기 엔진의 발명으로 자동 속도 제어가 필요하게 되었고, 링크 암에 의해 수직 스핀들에 부착된 회전 강철 볼 세트인 James Watt의 자체 설계 "원추형 진자" 가버너는 산업 표준이 되었습니다.이것은 맷돌 틈새 제어 [4]개념에 기초했다.
그러나 회전식 조속기 속도 제어는 현재 비례 제어로만 알려진 것의 단점이 분명한 다양한 부하 조건 하에서 여전히 가변적이었다.부하가 증가함에 따라 원하는 속도와 실제 속도 사이의 오차가 증가합니다.19세기에 주지사 운영에 대한 이론적 근거는 1868년 제임스 클러크 맥스웰에 의해 그의 유명한 논문인 "주지사에 대하여"에서 처음 기술되었다.그는 제어 안정성을 위한 수학적 기초를 탐구했고, 해답을 향해 나아갔지만 수학자들에게 [5][4]그 문제를 조사하도록 호소했다.이 문제는 1874년 에드워드 루트, 찰스 스투름, 1895년 아돌프 후르비츠에 의해 더욱 조사되었는데, 이들은 모두 제어 안정성 [4]기준의 확립에 기여했다.이후 응용에서 속도 조절기는 특히 1872년 와트의 원추형 진자 조절기를 이론적으로 분석한 미국의 과학자 윌러드 깁스에 의해 더욱 정교해졌다.
이 시기에 화이트헤드 어뢰의 발명은 주행 깊이의 정확한 제어를 필요로 하는 제어 문제를 야기했다.깊이 압력 센서만으로는 불충분한 것으로 판명되어, 어뢰의 전후 피치를 측정하는 진자가 깊이 측정과 조합되어 진자·히드로스타트 제어가 되었다.압력 제어는 제어 게인이 너무 높으면 불안정해지고 깊이 유지의 상당한 불안정성과 함께 오버슈트에 들어가는 비례 제어만 제공했습니다.진자는 현재 파생 제어로 알려진 것을 추가했는데, 이것은 어뢰의 급강하/등반 각도를 감지하여 진동을 완화시키고, 그에 따라 [6]깊이의 변화율을 감지합니다.이 개발은 (화이트헤드에 의해 그 행동의 실마리를 주지 않기 위해 "비밀"로 명명되었다)[7] 1868년경이었다.
1911년 Elmer Sperry가 선박 조향을 위해 개발한 PID 유형 컨트롤러의 또 다른 초기 사례입니다. 비록 그의 작업은 수학적인 [8]기반보다는 직관적이었습니다.
그러나 1922년이 되어서야 러시아계 미국인 엔지니어 니콜라스 미노르스키에 [9]의해 이론적인 분석을 통해 우리가 현재 PID 또는 3선 제어라고 부르는 공식적인 제어법이 처음 개발되었습니다.Minorsky는 미 해군을 위해 자동 조타 장치를 연구하고 설계했으며 조타수의 관찰에 기초했다.그는 조타수가 현재의 항로 오류뿐만 아니라 과거의 오류와 현재의 [10]변화율을 바탕으로 배를 조종했고, 이것은 Minorsky에 [4]의해 수학적으로 처리되었다고 언급했다.그의 목표는 일반적인 통제가 아니라 안정성이었고, 이는 문제를 상당히 단순화시켰다.비례 제어는 작은 장애에 대한 안정성을 제공했지만, 적분 항을 추가해야 하는 (정상 상태 오류로 인한) 강풍과 같은 지속적인 장애에 대처하기에는 불충분했다.마지막으로 안정성 및 제어를 개선하기 위해 파생항이 추가되었습니다.
USS 뉴멕시코호에서 조종사들이 방향타의 각속도를 조절하는 실험을 했다.PI 제어 결과 ±2°의 지속적인 요(각도 오차)가 발생했습니다.D 요소를 추가하면 대부분의 조타수가 [11]달성할 수 있는 것보다 더 나은 ±1/6°의 요 오차가 발생한다.
해군은 인사들의 반발로 결국 이 제도를 도입하지 않았다.비슷한 연구가 1930년대에 몇몇 다른 사람들에 의해 수행되고 출판되었다.
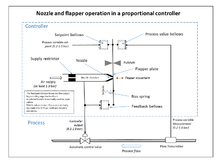
산업 통제
피드백 컨트롤러의 광범위한 사용은 네거티브 피드백 개념을 사용하는 광대역 고이득 증폭기가 개발되기 전까지는 실현 가능하지 않았습니다.이것은 1920년대 후반에 Harold Black에 의해 전화 공학 전자제품에서 개발되었지만 [4]1934년까지 출판되지 않았다.1930년 Foxboro Company의 Clesson E Mason은 1914년에 발명된 노즐과 플래퍼 고이득 공압 증폭기를 컨트롤러 출력의 부정적인 피드백과 결합하여 광대역 공압 컨트롤러를 발명했습니다.이를 통해 노즐 및 플래퍼 앰프의 선형 작동 범위가 극적으로 증가했으며, 통합 제어는 또한 통합 용어를 생성하는 정밀 블리딩 밸브와 벨로우즈를 사용하여 추가할 수 있었습니다.그 결과 피드백 [4]벨로우즈를 사용하여 비례 기능과 적분 기능을 모두 제공하는 "Stabilog" 컨트롤러가 탄생했습니다.적분항은 [12]Reset이라고 불립니다.나중에 파생항이 추가 벨로우즈 및 조정 가능한 오리피스에 의해 추가되었습니다.
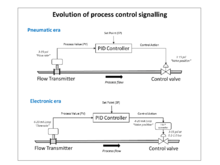
약 1932년부터 다양한 제어 어플리케이션에서 광대역 공압 컨트롤러의 사용이 급격히 증가하였다.공기 압력은 컨트롤러 출력을 생성하는 데 사용되었으며 다이어프램 작동 제어 밸브와 같은 프로세스 변조 장치에 전원을 공급하기 위해 사용되었습니다.그것들은 가혹한 산업 환경에서 잘 작동하며 위험한 장소에서는 폭발 위험이 없는 단순한 저유지보수 장치였다.개별 전자 제어기와 분산 제어 시스템이 등장하기 전까지 수십 년 동안 업계 표준이었습니다.
이러한 컨트롤러로 3~15psi(0.2~1.0bar)의 공압 산업 신호 표준이 확립되었습니다.이 표준은 장치가 선형 특성 내에서 작동하도록 보장하기 위해 0이 높아졌으며 제어 범위는 0-100%였습니다.
1950년대에 고이득 전자 증폭기가 저렴하고 신뢰성이 높아지면서 전자 PID 컨트롤러가 보급되어 10-50mA 및 4-20mA 전류 루프 신호로 공압 표준이 에뮬레이트되었습니다(후자는 업계 표준이 되었습니다).공압장 액추에이터는 프로세스 플랜트 환경에서 제어 밸브를 위한 공압 에너지의 이점 때문에 여전히 널리 사용되고 있습니다.
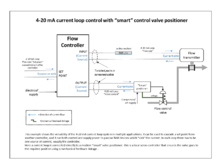
업계의 대부분의 최신 PID 제어는 Distributed Control System(DCS; 분산 제어 시스템), Programmable Logic Controller(PLC; 프로그래머블 로직 컨트롤러) 또는 이산 콤팩트 컨트롤러에서 컴퓨터 소프트웨어로 구현됩니다.
전자 아날로그 컨트롤러
전자 아날로그 PID 제어 루프는 디스크 드라이브의 헤드 포지셔닝, 전원 공급 장치의 전원 조절 또는 최신 지진계의 움직임 감지 회로와 같은 보다 복잡한 전자 시스템에서 종종 발견되었습니다.이산형 전자 아날로그 컨트롤러는 PID 알고리즘을 구현하기 위해 마이크로 컨트롤러 또는 FPGA를 사용하는 디지털 컨트롤러로 대체되었습니다.그러나 이산 아날로그 PID 컨트롤러는 레이저 다이오드 [13]컨트롤러와 같이 고대역폭 및 저노이즈 성능을 필요로 하는 틈새 애플리케이션에 여전히 사용됩니다.
제어 루프의 예
제어 루프에 의해 이동 및 배치될 수 있는 로봇[14] 암을 생각해 보십시오.전기모터는 가해지는 전·후진동력에 따라 암을 올리거나 내릴 수 있지만 암의 관성질량, 중력에 의한 힘, 들어올려야 할 하중이나 외부물체에 대한 작업 등 암에 가해지는 외력 때문에 동력이 단순한 위치기능이 될 수 없다.
- 감지 위치는 프로세스 변수(PV)입니다.
- 원하는 위치를 Setpoint(SP; 세트포인트)라고 부릅니다.
- PV와 SP의 차이는 에러(e)입니다.에러(e)는 암이 너무 낮거나 너무 높거나 어느 정도인지 수량화합니다.
- 프로세스에 대한 입력(모터의 전류)은 PID 컨트롤러의 출력입니다.이것은 조작 변수(MV) 또는 제어 변수(CV)라고 불립니다.
위치(PV)를 측정하여 설정점(SP)에서 감산함으로써 오차(e)를 찾아내고, 이 오차(e)로부터 모터(MV)에 공급하는 전류를 컨트롤러가 산출한다.
비례하다
분명한 방법은 비례 제어입니다. 모터 전류는 기존 오류에 비례하여 설정됩니다.단, 예를 들어 암이 다른 웨이트를 들어 올릴 필요가 있는 경우 이 방법은 실패합니다.중량이 클수록 아래쪽에 동일한 오차에 더 큰 힘을 가해야 하지만 위쪽에서 오류가 낮을 경우 더 작은 힘을 가해야 합니다.여기서 적분 및 파생항이 제 역할을 합니다.
일체형
적분항은 오류뿐만 아니라 오류가 지속된 시간과 관련하여 동작을 증가시킵니다.따라서, 가해진 힘이 오차를 0으로 만들기에 충분하지 않다면, 이 힘은 시간이 지날수록 증가할 것입니다.순수한 "I" 컨트롤러는 오류를 0으로 만들 수 있지만, 처음에는 반응이 느리고(중요해지는 시간에 따라 액션이 작기 때문에) 마지막에 잔혹합니다(오류가 0에 가까워지기 시작한 경우라도 양의 액션이 증가합니다).
오차가 작고 감소했을 때 너무 많은 적분을 적용하면 오버슈트가 발생합니다.오버슈팅 후 컨트롤러가 반대 방향으로 큰 보정을 적용하고 원하는 위치를 반복적으로 오버슈팅하면 출력은 일정, 증가 또는 감소하는 사인파 중 하나로 설정점 주변에서 진동합니다.시간이 지남에 따라 진폭이 증가하면 시스템이 불안정해집니다.감소하면 시스템은 안정적입니다.진동이 일정하게 유지되면 시스템은 약간 안정적입니다.
파생상품
파생항은 에러의 크기를 고려하지 않고(즉, 순수 D컨트롤러로는 시스템을 설정점으로 되돌릴 수 없음), 이 레이트를 제로로 하려고 하는 에러의 변화율을 고려합니다.오류 궤적을 수평선으로 평평하게 하여 가해지는 힘을 감쇠시키고 오버슈트를 감소시키는 것을 목표로 합니다(너무 큰 가해지는 힘에 의한 반대쪽 오류).
컨트롤 댐핑
원하는 위치(SP)에 시기적절하고 정확한 방법으로 제어된 도착을 달성하려면 제어된 시스템을 심각하게 감쇠해야 합니다.또한 잘 조정된 위치 제어 시스템이 제어된 모터에 필요한 전류를 공급하여 암이 필요한 위치에서 멀어지도록 하려는 외부 힘에 저항하기 위해 필요한 만큼 밀고 당기도록 합니다.설정점 자체는 PLC 또는 기타 컴퓨터 시스템과 같은 외부 시스템에 의해 생성될 수 있으므로 로봇 암이 수행할 것으로 예상되는 작업에 따라 지속적으로 달라질 수 있습니다.잘 조정된 PID 컨트롤 시스템을 사용하면 암이 이러한 변화하는 요구 사항을 최대한 충족할 수 있습니다.
장애에 대한 대응
컨트롤러가 오류가 0인 안정적인 상태(PV = SP)에서 시작하는 경우 컨트롤러에 의한 추가 변경은 프로세스에 영향을 미치는 다른 측정되거나 측정되지 않은 입력의 변경에 따라 달라집니다.MV 이외의 공정에 영향을 미치는 변수를 장애라고 합니다.일반적으로 컨트롤러는 장애를 거부하고 설정점 변경을 구현하기 위해 사용됩니다.암의 부하 변화는 로봇 암 제어 프로세스를 방해합니다.
적용들
이론적으로 컨트롤러는 측정 가능한 출력(PV), 해당 출력(SP)에 대해 알려진 이상값 및 관련 PV에 영향을 미치는 프로세스(MV) 입력을 가진 프로세스를 제어하기 위해 사용할 수 있습니다.컨트롤러는 업계에서 온도, 압력, 힘, [15]공급 속도, 유량, 화학 성분(성분 농도), 중량, 위치, 속도 및 실질적으로 측정이 존재하는 기타 모든 변수를 조절하기 위해 사용됩니다.
컨트롤러 이론
PID 제어 방식은 세 개의 수정 용어의 합이 조작 변수(MV)를 구성하는 이름을 따서 명명됩니다.비례항, 적분항 및 미분항이 합계되어 PID 컨트롤러의 출력이 계산됩니다.u {u(를 컨트롤러 출력으로 하면 PID 알고리즘의 최종 형식은 다음과 같습니다.
어디에
- p(\는 비례 이득, 조정 파라미터입니다.
- 는 적분 이득, 조정 파라미터입니다.
- d \ K _ { \ { } is 、파생 게인, 조정 파라미터,
- ) P - V () ( { e ( t ) = \ {- \ { PV } ( )는 에러입니다 (SP는 설정점, PV(t)는 프로세스 변수).
- t는 시간 또는 순간(현재)입니다.
- { \display }는 통합 변수입니다(시간 0부터 { t}까지의 값을 취합니다).
마찬가지로 PID 컨트롤러의 Laplace 도메인 내의 전송 함수는
서 ss는 복잡한 주파수입니다.
비례항
비례 항은 현재 오차 값에 비례하는 출력 값을 생성합니다.비례 반응은 오차에 비례 이득 상수라고 하는 상수p K를 곱하여 조정할 수 있습니다.
비례항은 다음과 같다.
비례 이득이 높으면 오차의 특정 변화에 대해 출력이 크게 변경됩니다.비례 게인이 너무 높으면 시스템이 불안정해질 수 있습니다(루프 조정 섹션 참조).반면 게인이 작을수록 큰 입력 오류에 대한 출력 응답이 작아지고 컨트롤러의 응답성이 떨어집니다.비례 이득이 너무 낮으면 시스템 장애에 대응할 때 제어 동작이 너무 작을 수 있습니다.튜닝 이론과 산업 관행은 비례항이 출력 [citation needed]변화의 대부분을 기여해야 한다는 것을 나타냅니다.
정상 상태 오류
정상 상태 오류는 원하는 최종 출력과 실제 [16]출력 간의 차이입니다.이를 구동하려면 0이 아닌 오류가 필요하기 때문에 비례 컨트롤러는 일반적으로 정상 [a]상태 오류로 작동합니다.정상 상태 오차(SSE)는 공정 게인에 비례하고 비례 게인에 반비례합니다.SSE는 설정점 AND 출력에 보정 바이어스 항을 추가함으로써 완화하거나 적분 항을 추가함으로써 동적으로 보정할 수 있다.
적분항
적분 항의 기여도는 오차의 크기와 오차의 지속 시간 모두에 비례합니다.PID 컨트롤러의 적분은 시간에 따른 순간 오류의 합계이며 이전에 수정했어야 할 누적 오프셋을 제공합니다.누적된 오류는 적분 게인(Ki)에 곱하여 컨트롤러 출력에 추가됩니다.
그 필수적인 용어에 의해서 주어진다.
그 필수적인 용어고 순수한 비례 조절계에서 발생할 수 있는 잔여 정상 편차들을 설정치를 위한 과정을 향해의 움직임을 가속화한다.누적된 오류 과거 이후로 적분 용어를 충족하며 하지만, 그것은 설정치 값(루프에 관한 부분 튜닝을 보)을 넘어가다. 현재 값을 일으킬 수 있다.
파생항
그 과정 오류의 파생 및 그 파생적 이득 해리 정수에 의해 변화의 이러한 비율을 곱한 오류의 시간에 걸쳐 경사를 결정해서 계산한다.는 파생적 용어의 전반적인 제어 조치에 기부의 크기는 미분 이득, 해리 정수라 한다.
그 파생적 용어에 의해서 주어진다.
대표 액션, 따라서settling 시간과 시스템의 안정성을 개선 시스템 작동 상태를 예측한다.[17][18]An ideal derivative is not causal, so that implementations of PID controllers include an additional low-pass filtering for the derivative term to limit the high-frequency gain and noise.한 추정에 의해 배치된 controllers[표창 필요한]–의 오직 25%에서 시스템 안정성에의 실세계 적용의 변수 영향 때문에 – 대표 액션 좀처럼 연습에 사용된다.
루프 튜닝
컨트롤 루프 조율의 제어 매개 변수의 조정은 원하는 제어 반응을 위한 최적의 가치에(비례 band/gain, 적분 gain/reset, 미분 gain/rate) 있다.안정성( 없는 무한한 진동)은 기본 요건으로 하지만 그 이상 다른 시스템, 다른 애플리케이션들을 다른 요건을 갖고, 및 요건 등 서로 충돌하는 다른 동작을 갖습니다.
비록 단지 세가지 매개 변수 및이 원칙적으로 설명하기 간단하다, PID튜닝이 어려운 문제 때문에 PID제어의 범위 안에서 복잡한 기준을 충족해야 한다.따라서, 루프 동조를 위해 다양한 방법, 특허의 더 정교한 기법은. 이 구간 루프 동조를 위해 전통, 수동 방법이 수록되어 있다.
PID 컨트롤러의 설계 및 조정은 개념적으로 직관적인 것으로 보이지만 짧은 과도나 높은 안정성 등 여러 가지(그리고 종종 상충되는) 목표를 달성해야 하는 경우에는 실제로 어려울 수 있습니다.PID 컨트롤러는 디폴트튜닝을 사용하여 허용 가능한 제어를 제공하는 경우가 많지만 일반적으로 신중한 튜닝을 통해 성능을 향상시킬 수 있으며 튜닝 불량으로 인해 성능이 저하될 수 있습니다.일반적으로 초기 설계는 폐쇄 루프 시스템이 원하는 대로 수행되거나 손상될 때까지 컴퓨터 시뮬레이션을 통해 반복적으로 조정해야 합니다.
일부 공정에는 비선형성이 있기 때문에 공정이 무부하 상태에서 시작될 때는 최대 부하 조건에서 잘 작동하는 모수가 작동하지 않습니다.이 문제는 게인 스케줄링을 통해 수정할 수 있습니다(동작 영역마다 다른 파라미터를 사용).
안정성.
PID 컨트롤러 파라미터(비례, 적분 및 미분항의 이득)가 잘못 선택되면 제어된 프로세스 입력이 불안정해질 수 있습니다.즉, 출력은 진동 유무에 관계없이 분산되며 포화 또는 기계적 파손에 의해서만 제한됩니다.불안정성은 특히 상당한 지연이 존재하는 경우 과도한 이득에 의해 발생합니다.
일반적으로 응답의 안정화가 필요하며 프로세스는 프로세스 조건과 설정점의 조합에 대해 진동해서는 안 됩니다.단, 한계 안정성(경계 진동)이 허용되거나 [citation needed]바람직한 경우도 있습니다.
수학적으로, 불안정성의 기원은 라플라스 [19]영역에서 볼 수 있습니다.
루프 전송 함수의 합계는 다음과 같습니다.
서 K { K는 PID 전송 함수, { G는 플랜트 전송 함수입니다. 루프 전송 기능이 일부 s s[19] 동안 분산되는 시스템은 불안정합니다.이는 K( ) ( ) -1 { K( =-인 에서 발생합니다. 일반적으로 이는 ( s) ( s ) 1 {G(s) {디스플레이 스타일 K(s) G(s) = 1일 때 합니다.고위상 시프트가 발생하는 주파수의 경우K ( )G () < { K ( ) ( ) < } 안정성이 보증됩니다.이 효과의 보다 일반적인 형식주의는 나이키스트 안정성 기준이라고 알려져 있다.
최적의 동작
과정 변화나 설정 값 변화에 대하는 최적의 행동은 응용 프로그램에 따라 다양하다.
2가지 기본적인 요건은 규제(장애인의 반응은 주어진 설정 값에 머무르–)하고 명령하는 추적(설정 값 변화 구현).이러한 용어가 얼마나 잘 가변이 원하는 값을 참조하십시오.명령 추적하는 특정 기준 상승 시간과settling 시간을 포함한다.예를 들면 이 안전하지 않은 몇 절차들은 공정 변수의 설정 값 없는 진행을 허락하여서는 안됩니다.다른 과정 쓴 에너지의 새로운 설정 값에 도달하는 주어지는지 생풀을 최소화해야 한다.
튜닝 방법의 개요
한 PID루프 동조를 위한 몇가지 방법이 있다.가장 효과적인 방법 일반적으론 다음 P선택할 때 나는, 그리고 D는 동적 모델 파라미터를 바탕으로 프로세스 모델 몇몇 형태의 개발을 포함한다.수동 튜닝 방법 비교적 긴 루프 시대와 함께 시스템, 특히 광대한 시간이 오래 걸릴 수 있다.
메서드의 선택은 대부분이 루프 오프라인으로 동조를 위한 것으로 여겨질 수 있는 및 시스템의 응답 시간에 따라 달라진다.그 시스템이 오프라인일 수 있는데 최고의 튜닝 방법 자주 입력에서는 한 단계 변화로, 시간의 함수 출력 측정 컨트롤 매개 변수를 결정할 이 응답을 사용하여 시스템 적용을 포함한다.[표창 필요한]
| 방법 | 이점 | 단점들 |
|---|---|---|
| 수동 조정 | 아니 수학, 온라인으로 요구했다. | 경험 많은 사람이 있어야 합니다.[표창 필요한] |
| Ziegler–Nichols [b] | Proven 방법, 온라인. | 프로세스 혼란, 시행착오, 매우 적극적인 튜닝.[citation needed] |
| 티루스 로이벤 | 실적이 있는 방법, 온라인.온라인. | 프로세스 혼란, 시행착오, 매우 적극적인 튜닝.[citation needed] |
| 소프트웨어 도구 | 온라인이든 오프라인이든 일관된 튜닝 – 컴퓨터 자동 제어 시스템 설계(CAUtoD) 기술을 사용할 수 있습니다. 밸브 및 센서 분석을 포함할 수 있습니다. 다운로드 전에 시뮬레이션을 수행할 수 있습니다. 또한 NSS(Non-Steady State) 튜닝을 지원할 수 있습니다. | 일부 비용 또는 훈련 관련.[21] |
| 코헨쿤 | 우수한 프로세스 모델. | 일부 수학, 오프라인, 1차 [citation needed]공정에만 적합합니다. |
| 오스트롬헤글룬드 | 자동 튜닝에 사용할 수 있습니다. 진폭이 최소이므로 이 방법은 프로세스 전환이 가장 적습니다. | 프로세스 자체는 본질적으로 [citation needed]진동적입니다. |
수동 조정
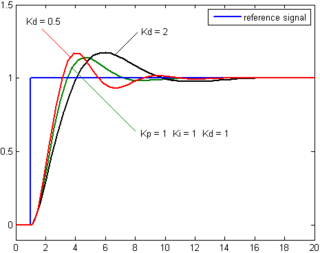
시스템이 온라인 상태를 유지해야 하는 경우 첫 번째 조정 방법은 }) 값을 0으로 하는 것입니다.루프의 출력이 진동할 때까지 p {\을(를) 증가시킨 다음 p {\를 "분기 진폭 감소" 유형의 응답에 대해 해당 값의 약 절반으로 합니다.그런 다음 를 늘린 후 충분한 시간 내에 오프셋이 수정되지만 값이 너무 크면 불안정해집니다.마지막으로 필요에 따라 부하 장애 후 루프가 기준치에 도달할 까지 K를 늘립니다.style 를 . 많으면 과도한 응답과 가 발생합니다고속 PID 루프 튜닝은 보통 설정점에 보다 빨리 도달하기 위해 약간 오버슈트를 합니다.단, 일부 시스템에서는 오버슈트를 받아들일 수 없습니다.이 경우 과잉 감쇠된 클로즈드 루프 시스템이 필요합니다.그러면 설정이 K_})의 절반보다 훨씬 작은 값으로 합니다.ng가 [citation needed]진동을 일으켰습니다.
| 파라미터 | 상승 시간 | 오버슈트 | 정산시간 | 정상 상태 오류 | 안정성. |
|---|---|---|---|---|---|
| 감소하다 | 증가하다 | 잔돈 | 감소하다 | 저하 | |
| 감소하다 | 증가하다 | 증가하다 | 제거하다 | 저하 | |
| 사소한 변경 | 감소하다 | 감소하다 | 이론상으로는 효과가 없다 | d \ K _ { } 작은 경우 |
지글러-니콜스법
또 다른 휴리스틱 튜닝 방법은 존 지글러와 나다니엘 B에 의해 도입된 지글러-니콜스 방법으로 알려져 있다. 1940년대의 니콜스.위의 방법과 같이\ K_ 은 처음에 0으로 설정됩니다.비례 이득은 루프의 출력이 지속적으로 진동하기 시작하는 궁극 이득인 에 도달할 때까지 증가합니다. 및 발진 는 다음과 같이 게인을 설정하는 데 사용됩니다.
| 제어 유형 | |||
|---|---|---|---|
| P | — | — | |
| PI | — | ||
| PID |
이러한 이득은 PID 컨트롤러의 이상적인 병렬 형식에 적용됩니다.표준 PID 형식에 적용할 경우 }) d의 적분 만 발진 에 의존합니다.
Cohen-Coon 파라미터
이 방법은 1953년에 개발되었으며 1차 + 시간 지연 모델을 기반으로 한다.Ziegler-Nichols 방식과 마찬가지로 일련의 조정 파라미터가 개발되어 감쇠율이 인 폐쇄루프 응답이 생성되었습니다.이 파라미터의 가장 큰 문제는 프로세스 파라미터의 작은 변경으로 인해 폐쇄루프 시스템이 불안정해질 수 있다는 것입니다..
릴레이 (오스트롬-)Hegglund) 방식
1984년 Karl Johan [24]Oström과 Tear Hegglund가 발표한 중계법은 뱅뱅 제어를 사용하여 프로세스를 임시로 작동시키고 그 결과 발생하는 진동을 측정합니다.출력은 (릴레이와 같이) 제어 변수의 두 값 사이에서 전환됩니다.이 값은 프로세스가 설정점을 통과하도록 선택해야 하지만 0%와 100%일 필요는 없습니다. 적절한 값을 선택하면 위험한 진동을 방지할 수 있습니다.
프로세스 변수가 설정값보다 낮은 경우 제어 출력은 더 높은 값으로 설정됩니다.설정값 이상으로 상승하면 제어출력이 낮은 값으로 설정됩니다.이상적으로는 출력 파형이 거의 정사각형이며 설정값 위와 아래에서 동일한 시간을 보내는 것입니다.결과 진동의 주기와 진폭을 측정하여 궁극적인 이득과 주기를 계산하는 데 사용되며, 이 주기는 지글러-니콜스 방법으로 공급됩니다.
구체적으로는 는 관측주기와 같다고 가정하고, 은 b / a \{u}= 4 b a 여기서 a는 프로세스 변수 진동의 진폭이며, b는 그 원인이 된 출력변화의 진폭이다.
릴레이 [25]방식에는 다양한 종류가 있습니다.
데드타임 모델을 사용한 첫 번째 주문
데드 타임을 수반하는 1차 프로세스의 전송 함수는 다음과 같습니다.
여기서p k는 프로세스 게인, θ는p 시간 상수, θ는 데드타임, u(s)는 스텝 변경 입력입니다.이 전송 함수를 시간 도메인으로 변환하면 다음과 같은 결과가 됩니다.
위의 파라미터와 동일한 파라미터를 사용합니다.
이 방법을 사용하여 출력을 측정할 수 있을 만큼 충분히 큰 스텝 변경 입력을 적용하는 것이 중요합니다. 단, 스텝 변경이 너무 크면 프로세스의 안정성에 영향을 줄 수 있습니다.또한 스텝 변경이 크면 장애로 인해 출력이 변경되지 않습니다(최선의 결과를 얻으려면 스텝 테스트를 수행할 때 장애의 최소화를 시도합니다).
1차 공정에 대한 모수를 결정하는 한 가지 방법은 63.2% 방법을 사용하는 것입니다.이 방법에서 프로세스 게인 k는p 출력의 변화를 입력의 변화로 나눈 값과 같다.데드 타임(Dead Time)은 스텝 변경이 발생한 시점부터 출력이 처음 변경된 시점까지의 시간입니다.시간 상수(θp)는 스텝 변경 후 출력이 새로운 정상 상태 값의 63.2%에 도달할 때까지 걸리는 시간입니다.이 방법을 사용하면 프로세스의 시간 [26]상수가 클 경우 새로운 정상 상태 값에 도달하는 데 시간이 걸릴 수 있습니다.
튜닝 소프트웨어
대부분의 현대 산업 시설은 위에 나온 수동 계산 방법을 사용하여 더 이상 루프를 조정하지 않습니다.대신 일관된 결과를 보장하기 위해 PID 튜닝 및 루프 최적화 소프트웨어를 사용합니다.이러한 소프트웨어 패키지는 데이터를 수집하고 프로세스 모델을 개발하며 최적의 조정을 제안합니다.일부 소프트웨어 패키지는 참조 변경에서 데이터를 수집하여 튜닝을 개발할 수도 있습니다.
수학적 PID 루프 튜닝은 시스템에서 임펄스를 유도한 다음 제어된 시스템의 주파수 응답을 사용하여 PID 루프 값을 설계합니다.응답 시간이 몇 분인 루프에서는 안정적인 루프 값 세트를 찾는 데만 며칠이 걸릴 수 있으므로 수학적 루프 튜닝을 권장합니다.최적의 값은 찾기 어렵습니다.일부 디지털 루프 컨트롤러는 매우 작은 설정값 변경이 프로세스에 전송되는 셀프 튜닝 기능을 제공하여 컨트롤러 자체가 최적의 튜닝 값을 계산할 수 있도록 합니다.
또 다른 접근방식은 지글러-니콜스 방법을 통해 초기값을 계산하고 수치 최적화 기법을 사용하여 더 나은 PID [27]계수를 찾습니다.
다른 퍼포먼스 기준에 따라 루프를 조정하기 위해 다른 수식을 사용할 수 있습니다.PID 튜닝 소프트웨어 및 하드웨어 [28]모듈에는 특허받은 많은 공식들이 포함되어 있습니다.
자동 PID 루프 튜닝소프트웨어의 진보로 다이내믹 또는 Non-Steady State(NSS; 비스테디 스테이트) 시나리오에서 PID 루프를 튜닝하기 위한 알고리즘도 제공됩니다.소프트웨어는 교란을 통해 프로세스의 역학을 모델링하고 이에 대한 [29]PID 제어 파라미터를 계산합니다.
제한 사항
PID 컨트롤러는 많은 제어 문제에 적용할 수 있으며 대부분의 경우 개선이나 거친 튜닝 없이 만족스러운 성능을 발휘하지만 일부 애플리케이션에서는 성능이 저하될 수 있으며 일반적으로 최적의 제어를 제공하지 않습니다.PID 제어의 근본적인 어려움은 파라미터가 일정하고 프로세스에 대한 직접적인 지식이 없는 피드백 제어 시스템이기 때문에 전반적인 성능이 반응적이며 타협적이라는 것입니다.PID 제어는 프로세스의 모델이 없는 옵서버에서 가장 좋은 컨트롤러이지만 옵서버에 의존하지 않고 프로세스의 액터를 명시적으로 모델링함으로써 더 나은 성능을 얻을 수 있습니다.
PID 컨트롤러를 단독으로 사용하면 제어 시스템이 제어 설정점 값을 오버슈트, 진동 또는 헌트하지 않도록 PID 루프 게인을 줄여야 할 때 성능이 저하될 수 있습니다.또한 비선형성이 존재하는 경우, 규제 대 응답 시간의 트레이드오프(trade-off)가 발생할 수 있으며, 프로세스 동작의 변화에 반응하지 않으며(예: 프로세스가 예열된 후 변화), 큰 장애에 대한 대응이 지연됩니다.
가장 중요한 개선사항은 피드포워드 제어와 시스템에 대한 지식을 통합하고 PID를 사용하여 오류를 제어하는 것입니다.또는 파라미터 변경(다른 사용 사례에서 게인 스케줄링 또는 퍼포먼스에 따라 적응적으로 수정), 측정 개선(샘플링 속도, 정밀도 및 정확도 향상, 필요에 따라 로우패스 필터링) 또는 여러 PID 컨트롤러를 캐스케이드하는 등 보다 사소한 방법으로 PID를 변경할 수 있습니다.
선형성과 대칭성
PID 컨트롤러는 제어하는 루프가 선형이고 대칭일 때 가장 잘 작동합니다.따라서 비선형 및 비대칭 시스템에서 성능이 저하됩니다.
예를 들어 유량 제어 애플리케이션에서 비선형 밸브는 가변 루프 감도를 발생시켜 불안정성을 방지하기 위한 감쇠 조치가 필요합니다.한 가지 해결책은 제어 알고리즘에서 밸브의 비선형 특성을 사용하여 이를 보완하는 것입니다.
예를 들어, 비대칭 적용은 (발열 요소를 통해) 능동 난방만을 사용하는 HVAC 시스템의 온도 제어이며, 수동 냉각만 사용할 수 있습니다.제어 온도를 낮추려는 경우 난방 출력은 꺼지지만 제어 출력으로 인해 활성 냉각은 이루어지지 않습니다.따라서 온도가 상승하는 오버슈트는 느리게 보정될 뿐이며 제어 출력에 의해 강제로 하향 보정될 수 없습니다.이 경우 오버슈트를 방지하거나 줄이기 위해 PID 컨트롤러를 오버 덤프하도록 조정할 수 있지만, 이 경우 온도 상승의 안착 시간이 설정 지점으로 증가하여 성능이 저하됩니다.이 응용 프로그램의 제어 품질 저하는 능동 냉각 응용 프로그램을 통해 해결할 수 있습니다.
파생항 잡음
파생항의 문제는 높은 주파수 측정 또는 프로세스 노이즈를 증폭하여 출력에 큰 변화를 일으킬 수 있다는 것입니다.저역 통과 필터로 측정을 필터링하여 고주파 노이즈 성분을 제거하는 것이 종종 유용합니다.로패스 필터링과 파생 제어는 서로 상쇄할 수 있기 때문에 필터링의 양은 한정되어 있습니다.따라서 저소음 계측이 중요할 수 있다.필터링 효율과 실제 [30]성능을 향상시키는 비선형 중앙 필터를 사용할 수 있다.경우에 따라서는 컨트롤 손실 없이 디퍼렌셜 밴드를 끌 수 있습니다.이는 PID 컨트롤러를 PI 컨트롤러로 사용하는 것과 동일합니다.
알고리즘의 변경
기본 PID 알고리즘은 PID 형식에 대한 사소한 수정으로 해결된 제어 응용 프로그램에서 몇 가지 과제를 제시합니다.
일체형 와인딩
이상적인 PID 구현에서 발생하는 일반적인 문제 중 하나는 일체형 와인드업입니다.설정점의 큰 변경에 따라 적분항은 규제변수의 최대값(윈드업)보다 큰 오차를 누적할 수 있습니다.따라서 시스템은 오버슈팅되어 이 누적된 오차가 해소될 때까지 계속 증가합니다.이 문제는 다음 방법으로 해결할 수 있습니다.
- PV가 제어 가능 영역에 진입할 때까지 통합 비활성화
- 적분 항이 미리 결정된 한계를 초과하거나 미만으로 누적되지 않도록 함
- 적분항을 역계산하여 조정기 출력을 실현 가능한 [31]범위 내에서 제한합니다.
알려진 장애로부터의 오버슈팅
예를 들어 PID 루프는 시스템이 안정화된 전기 저항로의 온도를 제어하기 위해 사용됩니다.이제 문을 열고 차가운 것을 아궁이에 넣으면 온도가 설정값 아래로 떨어집니다.컨트롤러의 통합 기능은 양의 방향으로 또 다른 오류를 발생시킴으로써 오류를 보완하는 경향이 있습니다.이러한 오버슈트는 제어 루프가 일반적으로 용해로를 재가열해야 하는 시간 동안 도어를 연 후 통합 기능을 동결함으로써 방지할 수 있습니다.
PI 컨트롤러
PI 컨트롤러(비례 적분 컨트롤러)는 오류의 도함수(D)가 사용되지 않는 PID 컨트롤러의 특수한 경우입니다.
컨트롤러의 출력은 다음과 같습니다.
여기서 \는 설정점(SP)에서 실제 측정값(PV)의 오차 또는 편차입니다.
PI 컨트롤러는 Laplace 연산자가 참여하는 "흐름도" 상자를 사용하여 Simulink 또는 Xcos 등의 소프트웨어에서 쉽게 모델링할 수 있습니다.
어디에
- ({ G = 비례 이득
- = 적분 이득
G G에 값을 설정하는 것은 오버슈트 감소와 안착 시간 증가 사이의 트레이드오프인 경우가 많습니다.
파생 작용이 부족하면 데이터가 노이즈가 있는 경우 시스템이 정상 상태에서 더 안정될 수 있습니다.이는 미분 작용이 입력의 고주파 항에 더 민감하기 때문입니다.
파생 작용이 없으면 PI 제어 시스템은 실제(비노이즈)에 대한 응답성이 떨어지고 상태 변화가 비교적 빠르기 때문에 시스템이 설정점에 도달하는 속도가 잘 조정된 PID 시스템보다 느리고 섭동에 대한 응답 속도가 느려집니다.
데드밴드
많은 PID 루프가 기계 장치(예: 밸브)를 제어합니다.기계적 유지보수는 주요 비용이 될 수 있으며, 마모 리드는 입력 신호에 대한 기계적 응답에서 고착 또는 백래시의 형태로 열화를 제어할 수 있습니다.기계적 마모율은 주로 장치를 얼마나 자주 작동시켜 변경하느냐에 따라 달라집니다.마모가 중요한 경우 PID 루프에 출력(밸브)의 활성화 주파수를 줄이기 위한 출력 데드밴드가 있을 수 있습니다.이것은 (정의된 데드밴드 범위 내에서) 변경이 적은 경우 출력을 일정하게 유지하도록 컨트롤러를 수정함으로써 실현됩니다.실제 출력이 변경되기 전에 계산된 출력이 데드밴드를 벗어나야 합니다.
설정점 스텝 변경
시스템에 큰 설정값 변경 등 오류가 순간적으로 증가하는 경우 비례항과 파생항이 출력에 과도한 움직임을 일으킬 수 있습니다.파생항의 경우, 이는 오차의 도함수를 취하기 때문이며, 이는 순간적인 단계 변경의 경우 매우 크다.그 결과, 일부 PID 알고리즘에서는, 다음의 몇개의 수정이 포함되어 있습니다.
- 설정점 램프
- 이 변경에서 설정점은 선형 또는 1차 차분 램프 함수를 사용하여 오래된 값에서 새롭게 지정된 값으로 서서히 이동한다.이것에 의해, 간단한 스텝 변경으로 발생하는 중단이 회피됩니다.
- 공정 변수의 도함수
- 이 경우 PID 컨트롤러는 오차의 도함수가 아니라 측정된 프로세스 변수(PV)의 도함수를 측정합니다.이 수량은 항상 연속적입니다(즉, 설정값이 변경되어 스텝이 변경되지 않습니다).이 변경은 설정값 가중치의 단순한 경우입니다.
- 설정값 가중치
- 설정값 가중치는 컨트롤러의 비례 및 파생 요소 오류의 설정값에 조정 가능한 요인(보통 0 ~ 1)을 추가합니다.정상 상태 제어 오류를 방지하려면 적분 항의 오류가 진정한 제어 오류여야 합니다.이 두 개의 추가 파라미터는 로드 장애 및 측정 노이즈에 대한 응답에 영향을 주지 않으며 컨트롤러의 설정값 응답을 개선하도록 조정할 수 있습니다.
피드 포워드
제어 시스템 성능은 PID 컨트롤러의 피드백(또는 폐쇄 루프) 제어와 피드포워드(또는 개방 루프) 제어를 결합하여 개선할 수 있습니다.시스템에 대한 지식(예: 원하는 가속도 및 관성)을 전달하고 PID 출력과 결합하여 전체 시스템 성능을 개선할 수 있습니다.대부분의 경우 피드 전송 값만 컨트롤러 출력의 대부분을 제공할 수 있습니다.PID 컨트롤러는 주로 설정점(SP)과 오픈 루프 제어에 대한 시스템 응답 사이에 남아 있는 차이 또는 오류를 보상해야 합니다.피드포워드 출력은 프로세스 피드백의 영향을 받지 않기 때문에 제어 시스템을 진동시킬 수 없으므로 안정성에 영향을 주지 않고 시스템 응답을 향상시킬 수 있습니다.피드 포워드는 설정점과 추가로 측정된 장애에 기반할 수 있습니다.설정값 가중치는 피드 포워드의 단순한 형태입니다.
예를 들어 대부분의 모션 컨트롤 시스템에서 제어 중인 기계적 부하를 가속하려면 액추에이터로부터 더 많은 힘이 필요합니다.속도 루프 PID 컨트롤러를 사용하여 부하 속도를 제어하고 액추에이터에 의해 가해지는 힘을 명령하는 경우 원하는 순간 가속을 취하여 해당 값을 적절히 스케일링하여 PID 속도 루프 컨트롤러의 출력에 추가하는 것이 좋습니다.즉, 부하가 가속 또는 감속될 때마다 피드백 값에 관계없이 액추에이터로부터 비례적인 양의 힘이 명령됩니다.이 경우 PID 루프는 피드백 정보를 사용하여 결합된 출력을 변경하여 프로세스 설정점과 피드백 값 간의 나머지 차이를 줄입니다.결합된 개방 루프 피드포워드 컨트롤러와 폐쇄 루프 PID 컨트롤러가 함께 작동하면 보다 응답성이 높은 제어 시스템을 제공할 수 있습니다.
범플리스 조작
PID 컨트롤러는 파라미터 [32]변경을 통해 일관된 프로세스 출력을 유지하기 위해 적분 어큐뮬레이터 기간을 재계산하는 "범플리스" 초기화 기능으로 구현되는 경우가 많습니다.부분적인 실장은 에러를 저장하고 적분 게인에 의한 사후 곱셈을 하는 것이 아니라 적분 게인에 의한 적분 게인을 저장하는 것입니다.이로 인해 게인이 변경되었을 때 출력은 중단되지만 P 또는 D 게인은 중단되지 않습니다.
기타 개선 사항
피드포워드와 더불어 PID 컨트롤러는 PID 게인 스케줄링(다른 동작 조건에서의 파라미터 변경), 퍼지 논리 또는 계산 동사 [33][34]로직과 같은 방법을 통해 확장되는 경우가 많습니다.컨트롤러에 접속되어 있는 계측으로부터, 한층 더 실용적인 애플리케이션상의 문제가 발생할 가능성이 있습니다.적절한 제어 성능을 달성하기 위해서는 충분한 샘플링 속도, 측정 정밀도 및 측정 정확도가 필요합니다.PID 컨트롤러를 개선하기 위한 또 다른 새로운 방법은 분수 차수를 이용하여 자유도를 높이는 것이다.인테그레이터와 차별화 요소의 순서로 컨트롤러의 [35]유연성이 향상됩니다.
캐스케이드 제어
PID 컨트롤러의 특징적인 장점은 2개의 PID 컨트롤러를 함께 사용하여 더 나은 동적 성능을 얻을 수 있다는 것입니다.이를 캐스케이드 PID 제어라고 합니다.한쪽 컨트롤러가 다른 한쪽 컨트롤러의 설정점을 조정하도록 배치될 때 2개의 컨트롤러가 캐스케이드 형태로 배치됩니다.PID 컨트롤러는 외부 루프 컨트롤러로 기능하며, 유체 레벨이나 속도 등의 1차 물리적 파라미터를 제어합니다.다른 한쪽 컨트롤러는 내부 루프 컨트롤러로서 기능하며, 외부 루프 컨트롤러의 출력을 설정점으로 읽어내고, 일반적으로 보다 빠르게 변화하는 파라미터, 유량 또는 가속을 제어합니다.캐스케이드된 PID [vague]컨트롤러를 사용함으로써 컨트롤러의 동작 주파수가 증가하고 객체의 시간 상수가 감소함을 수학적으로[citation needed] 증명할 수 있습니다.
예를 들어, 온도 제어 순환 욕조에는 캐스케이드 형태의 2개의 PID 컨트롤러가 있으며, 각 컨트롤러에는 자체 열전대 온도 센서가 있습니다.외부 컨트롤러는 히터에서 멀리 떨어진 곳에 위치한 열전대를 사용하여 물의 온도를 제어합니다. 이 열전대는 물의 대부분을 정확하게 판독합니다.이 PID 컨트롤러의 오차항은 원하는 욕조 온도와 측정된 온도 간의 차이입니다.히터를 직접 제어하는 대신 외부 PID 컨트롤러는 내부 PID 컨트롤러의 히터 온도 목표를 설정합니다.내부 PID 컨트롤러는 히터에 부착된 열전대를 사용하여 히터의 온도를 제어합니다.내부 컨트롤러의 오차항은 이 히터 온도 설정값과 측정된 히터 온도 간의 차이입니다.이 출력은 실제 히터를 이 설정값 근처에 유지하도록 제어합니다.
두 컨트롤러의 비례, 적분 및 미분 용어는 매우 다릅니다.외부 PID 컨트롤러에는 긴 시간 상수가 있습니다. 탱크 내의 모든 물은 가열 또는 냉각되어야 합니다.내부 루프는 훨씬 빠르게 반응합니다.각 컨트롤러는 자신이 제어하는 시스템의 물리적 특성(탱크 전체 또는 히터만의 열 전달 및 열 질량)에 맞게 튜닝할 수 있어 전체 [36][37]응답성이 향상됩니다.
대체 용어 및 형식
이 섹션은 어떠한 출처도 인용하지 않습니다.(2012년 12월 (이 및 에 대해 ) |
표준형식과 병렬형식(이상형식)
업계에서 가장 자주 볼 수 있는 PID 컨트롤러의 형태와 조정 알고리즘에 가장 관련된 것이 표준 형식입니다. 형식에서 Kp { 은 t{ I_ D t {D_{\{out 용어에 적용되어 다음과 같은 결과를 얻을 수 있습니다.
어디에
- T_는 적분시간입니다.
- Td { T _ { } the t 。
이 표준 형식에서 매개 변수는 명확한 물리적 의미를 가집니다.특히 내부 합계는 미래 및 과거 오류를 보상하는 새로운 단일 오류 값을 생성합니다.비례 오차항은 전류 오차입니다.파생 컴포넌트 용어에서는 루프 제어가 변경되지 않은 것으로 가정하여 향후 T 초(또는 샘플)의 에러값을 예측하려고 합니다.통합 컴포넌트는 모든 과거의 에러의 합계를 보상하기 위해 에러값을 조정합니다.는 Ti( 샘플)\ T_초 에 에러를 완전히 제거할 목적으로 합니다.그 결과 보정된 단일 오차 값은 단일 p만큼 스케일링되어 제어 변수를 계산합니다.
컨트롤러 이론 섹션에 표시된 병렬 형식
게인 매개변수는 / { K_} =i} K d \ K_} =를 표준 형식의 매개변수와 관련된다.매개변수가 단순한 이득으로 취급되는 이 병렬 형식은 가장 일반적이고 유연한 형식입니다.단, 파라미터가 물리적인 동작에 가장 약한 관계를 갖는 형태이기도 하며 일반적으로 PID 컨트롤러의 이론적인 처리를 위해 예약되어 있습니다.표준 형태는 수학적으로 조금 더 복잡하지만 산업에서는 더 일반적입니다.
비례 대역인 상호 이득
대부분의 경우 PID 컨트롤러에 의한 조작 변수 출력은 가능한 최대값의 0~100% 사이의 무차원 분율이며, 실제 단위(펌핑 속도 또는 히터 전력의 와트 등)로의 변환은 PID 컨트롤러 외부에 있습니다.그러나 공정 변수는 온도와 같은 차원 단위로 표시됩니다.이 경우 를 "도당 출력"이 아니라 비례 100 의 역수 형식으로 표현하는 것이 일반적입니다. 즉, 출력이 0%에서 1로 바뀌는 범위입니다.이 범위를 벗어나면 출력이 포화 상태, 풀오프 또는 풀온 상태가 됩니다.이 밴드가 좁을수록 비례 이득이 높아집니다.
PV에 기초하는 파생 작용
대부분의 상용 제어 시스템에서 파생 작용은 오류보다는 프로세스 변수에 기초합니다.즉, 설정점의 변경은 파생상품 작용에 영향을 미치지 않는다.이는 알고리즘의 디지털버전으로 인해 설정점이 변경되었을 때 대량의 불필요한 스파이크가 발생하기 때문입니다.설정값이 일정할 경우 PV의 변경은 오류의 변경과 동일합니다.따라서 이 변경은 프로세스 장애에 대한 컨트롤러의 응답 방식에는 영향을 주지 않습니다.
PV에 기반한 비례 작용
대부분의 상용 제어 시스템은 프로세스 변수만을 기반으로 비례 작용도 수행할 수 있는 옵션을 제공합니다.즉, 설정점 변경에 응답하는 것은 일체형 액션뿐입니다.알고리즘의 변경은 프로세스 장애에 대한 컨트롤러의 응답 방식에는 영향을 주지 않습니다.PV에 비례하는 액션을 베이스로 하는 것으로, 설정 포인트의 급격한 변경에 의해서 발생하는, 즉석에서 매우 큰 출력의 변화가 없어집니다.프로세스와 조정에 따라 설정점 단계에 대한 응답에 도움이 될 수 있습니다.
King은[38] 효과적인 차트 기반 방법을 설명합니다.
라플라스 형태
경우에 따라서는 PID 레귤레이터를 Laplace 변환 형식으로 기술하는 것이 편리합니다.
PID 컨트롤러가 Laplace 형태로 작성되어 제어된 시스템의 전송 기능을 가지면 시스템의 폐쇄 루프 전송 기능을 쉽게 결정할 수 있다.
시리즈/인터랙션 폼
PID 컨트롤러의 또 다른 표현은 직렬 또는 상호 작용 형식입니다.
여기서 매개 변수는 표준 형식의 매개 변수와 관련이 있습니다.
- p } = \ }, { T_} = \ _ { \ ,
와 함께
- α)1+τ dτ 나는{\displaystyle \alpha =1+{\frac{\tau_{d}}{\tau_{나는}}}}.
이 양식은 본질적으로 시리즈에 PD와 PI제어 장치로 구성되어 있다.이 적분은 컨트롤러의 편견을 계산하기 위해 요구한 것으로서 이 형태는 능력multi-controller 앞선 제어력 계획의 적절한 구현에 사용할 필요한 외부 바이어스 값을 추적할 수 있습니다.
개별 실장
한 microcontroller(maincontrolunit)또는 FPGA기기에 PID제어기의 디지털 구현을 설계하는 분석은 PID제어기의 표준 서식 discretized 것을 요구한다.[39]일차 파생 상품에 대한 Approximations 낙후된 플레이어와 한정되어 차이에 의해 만들어진다.U(t){\displaystyle u(t)}과 e(t){\displaystyle e(t)}이 있t{\displaystyle \Delta지},, k는 샘플 지수 Δ 시기로 discretized.
PID방정식은 뉴턴의 표기법을 사용하여 양쪽 Differentiating:을 준다.
대표 조건 as,하고 있다.
그렇게,
다시 gives, 뒤로 차이를 적용하는 것.
상기 방정식의 용어를 단순화 및 재그룹화함으로써 최종적으로 MCU에서 이산화된 PID 컨트롤러를 구현하기 위한 알고리즘을 얻을 수 있다.
또는 다음과 같이 입력합니다.
.t. / / { d } = { } / _ { } 、
주의: 이 메서드는 u ( ) p () + i 0 ( ) + ( ) + 0 ( \ u ( t ) =_ { \ { + { \ { { } } \ } () 。t에 의존하지 않는 상수.이 상수는 규제 루프에 대한 시작 및 중지 컨트롤을 사용하려는 경우 유용합니다.예를 들어 Kp, Ki 및 Kd를 0으로 설정하면 u(t)는 일정하게 유지됩니다.마찬가지로 오류가 이미0에 가깝고 u(t) non null에 가까운 시스템에서 규제를 시작할 경우 출력을 0으로 전송할 수 없습니다.
유사 코드
다음으로 평신도들이 쉽게 이해할 수 있는 매우 단순하고 명시적인 의사 코드 그룹을 나타냅니다.
- Kp - 비례 이득
- Ki - 적분 이득
- Kd - 파생 이득
- dt - 루프 간격 시간
previous_error := 0 적분 := 0 루프: 오류 := setpoint - measured_value propertional := 오류; 적분 := (오류 - 이전_error) / dt 출력 := Kp × 비례 + Ki × 적분 + Ki × 적분 + Kd × 파생물 previ_ervi _ error := 오류 := wait ( dt ) geto lo lo lo lo lo lo lo lo lo lo lo lo lo lo lo lo lo lo lo
PID 알고리즘을 실장하는 보다 복잡하고 명시적이지 않은 소프트웨어 루프를 다음에 나타냅니다.
A0 := Kp + Ki*dt + Kd/dt A1 := -Kp - 2*Kd/dt A2 := Kd/dt 오류 [2] := 0 // e(t-2) 오류 [1] := 0 /(t-1) 오류 [0] := 0 /// e(t) 오류 [0] : = 0 //(t) 일반적으로 u(t) 출력됩니다.[2] wait(dt) goto 루프
여기서 Kp는 무차원 수치이고 Ki는 s-({ s로 표현되며 Kd는 s로 표현된다.액튜에이터와 측정값이 동일한 단위가 아닌 조절(예를 들어 밸브를 제어하는 모터를 이용한 온도 조절)을 할 때 단위 변환 계수로 Kp, Ki, Kd를 보정할 수 있다.Ki를 역수 형태(통합 시간)로 사용하는 것도 흥미로울 수 있다.상기의 실장에서는 I 전용 컨트롤러를 실행할 수 있습니다.이 경우 도움이 될 수 있습니다.
현실에서는 D-to-A로 변환되어 조작변수(MV)로 제어되는 프로세스로 전달됩니다.현재 오류는 다음 미분에서 재사용하기 위해 다른 곳에 저장되며 프로그램은 시작 후 dt초가 경과할 때까지 대기하며 루프가 다시 시작되고 PV 및 설정점의 새 값을 읽고 [40]오류의 새 값을 계산합니다.
실제 코드의 경우, 「wait(dt)」의 사용은 부적절할 가능성이 있습니다.이는 알고리즘 자체에 의해 루프중에 걸리는 시간이나, 보다 중요한 것은 알고리즘을 지연시키는 프리엠프션이 고려되지 않기 때문입니다.
A common issue when using is the response to the derivative of a rising or falling edge of the setpoint as shown below: 
일반적인 회피책은 시간 상수 /N {의 로우패스 필터를 사용하여 파생 동작을 필터링하는 것입니다. 서3 < < = \ 3 < = N > <= N 。
파생 모델에 무한 임펄스 응답 필터를 사용하는 위의 알고리즘의 변형입니다.
A0 := Kp + Ki*dt A1 := -Kp 오류 [2] := 0 // e(t-2) 오류 [1] := 0 // e(t-1) 오류 [0] := 0 // u0 / 보통 액추에이터 A0d = Kd/t A0 d의 현재 값입니다.:= error[0] error[0] := setpoint - measured_value // PI 출력 := output [0] + A0 * error[1] // 필터링된 D1 = d0 d0 = A0d * error[0] + A1d * error[2] fd fd1 = 0 fd fd fd1 = fd0 fd0 fd1 = 0고토루프
「 」를 참조해 주세요.
메모들
레퍼런스
- ^ Araki, M. (2009). "CONTROL SYSTEMS, ROBOTICS AND AUTOMATION – Volume VII - PID Control" (PDF). Japan: Kyoto University.
- ^ Hills, Richard L (1996), Power From the Wind, Cambridge University Press
- ^ Richard E. Bellman (December 8, 2015). Adaptive Control Processes: A Guided Tour. Princeton University Press. ISBN 9781400874668.
- ^ a b c d e f Bennett, Stuart (1996). "A brief history of automatic control" (PDF). IEEE Control Systems Magazine. 16 (3): 17–25. doi:10.1109/37.506394. Archived from the original (PDF) on 2016-08-09. Retrieved 2014-08-21.
- ^ Maxwell, J. C. (1868). "On Governors" (PDF). Proceedings of the Royal Society. 100.
- ^ Newpower, Anthony (2006). Iron Men and Tin Fish: The Race to Build a Better Torpedo during World War II. Praeger Security International. ISBN 978-0-275-99032-9. p. 인용.
- ^ Sleeman, C. W. (1880), Torpedoes and Torpedo Warfare, Portsmouth: Griffin & Co., pp. 137–138,
which constitutes what is termed as the secret of the fish torpedo.
- ^ "A Brief Building Automation History". Archived from the original on 2011-07-08. Retrieved 2011-04-04.
- ^ Minorsky, Nicolas (1922). "Directional stability of automatically steered bodies". Journal of the American Society for Naval Engineers. 34 (2): 280–309. doi:10.1111/j.1559-3584.1922.tb04958.x.
- ^ Bennett 1993, 페이지 67 : 1993
- ^ Bennett, Stuart (June 1986). A history of control engineering, 1800-1930. IET. pp. 142–148. ISBN 978-0-86341-047-5.
- ^ Shinskey, F Greg (2004), The power of external-reset feedback (PDF), Control Global
- ^ Neuhaus, Rudolf. "Diode Laser Locking and Linewidth Narrowing" (PDF). Retrieved June 8, 2015.
- ^ "Position control system" (PDF). Hacettepe University Department of Electrical and Electronics Engineering.
- ^ Kebriaei, Reza; Frischkorn, Jan; Reese, Stefanie; Husmann, Tobias; Meier, Horst; Moll, Heiko; Theisen, Werner (2013). "Numerical modelling of powder metallurgical coatings on ring-shaped parts integrated with ring rolling". Material Processing Technology. 213 (1): 2015–2032. doi:10.1016/j.jmatprotec.2013.05.023.
- ^ Lipták, Béla G. (2003). Instrument Engineers' Handbook: Process control and optimization (4th ed.). CRC Press. p. 108. ISBN 0-8493-1081-4.
- ^ "Introduction: PID Controller Design". University of Michigan.
- ^ Tim Wescott (October 2000). "PID without a PhD" (PDF). EE Times-India.
{{cite journal}}:Cite 저널 요구 사항journal=(도움말) - ^ a b Bechhoefer, John (2005). "Feedback for Physicists: A Tutorial Essay On Control". Reviews of Modern Physics. 77 (3): 783–835. Bibcode:2005RvMP...77..783B. CiteSeerX 10.1.1.124.7043. doi:10.1103/revmodphys.77.783.
- ^ Atherton, Drek P (December 2014). "Almost Six Decades in Control Engineering". IEEE Control Systems Magazine. 34 (6): 103–110. doi:10.1109/MCS.2014.2359588. S2CID 20233207.
- ^ Li, Y. 등(2004) CAutoCSD - 진화적 검색 및 최적화가 가능한 컴퓨터 자동 제어 시스템 설계, Int J Automation and Computing, vol.1, No.1, 페이지 76-88.ISSN 1751-8520
- ^ Kiam Heong Ang; Chong, G.; Yun Li (2005). "PID control system analysis, design, and technology" (PDF). IEEE Transactions on Control Systems Technology. 13 (4): 559–576. doi:10.1109/TCST.2005.847331. S2CID 921620.
- ^ Jinghua Zhong (Spring 2006). "PID Controller Tuning: A Short Tutorial" (PDF). Archived from the original (PDF) on 2015-04-21. Retrieved 2011-04-04.
{{cite journal}}:Cite 저널 요구 사항journal=(도움말) - ^ Åström, K.J.; Hägglund, T. (July 1984). "Automatic Tuning of Simple Regulators". IFAC Proceedings Volumes. 17 (2): 1867–1872. doi:10.1016/S1474-6670(17)61248-5.
- ^ Hornsey, Stephen (29 October 2012). "A Review of Relay Auto-tuning Methods for the Tuning of PID-type Controllers". Reinvention. 5 (2).
- ^ Bequette, B. Wayne (2003). Process Control: Modeling, Design, and Simulation. Upper Saddle River, New Jersey: Prentice Hall. p. 129. ISBN 978-0-13-353640-9.
- ^ Heinänen, Eero (October 2018). A Method for automatic tuning of PID controller following Luus-Jaakola optimization (PDF) (Master's Thesis ed.). Tampere, Finland: Tampere University of Technology. Retrieved Feb 1, 2019.
- ^ Li, Yun; Ang, Kiam Heong; Chong, Gregory C.Y. (February 2006). "Patents, software, and hardware for PID control: An overview and analysis of the current art" (PDF). IEEE Control Systems Magazine. 26 (1): 42–54. doi:10.1109/MCS.2006.1580153. S2CID 18461921.
- ^ Soltesz, Kristian (January 2012). On Automation of the PID Tuning Procedure (PDF) (Licentiate theis). Lund university. 847ca38e-93e8-4188-b3d5-8ec6c23f2132.
- ^ Li, Y. and Ang, K.H. 및 Chong, G.C.Y. (2006) PID 제어 시스템 분석 및 설계 - 문제, 해결 방법 및 미래 방향.IEEE Control Systems Magazine, 26 (1) 페이지 32-41.ISSN 0272-1708
- ^ Cooper, Douglas. "Integral (Reset) Windup, Jacketing Logic and the Velocity PI Form". Retrieved 2014-02-18.
- ^ Cooper, Douglas. "PI Control of the Heat Exchanger". Practical Process Control by Control Guru. Retrieved 2014-02-27.
- ^ Yang, T. (June 2005). "Architectures of Computational Verb Controllers: Towards a New Paradigm of Intelligent Control". International Journal of Computational Cognition. 3 (2): 74–101. CiteSeerX 10.1.1.152.9564.
- ^ Liang, Yilong; Yang, Tao (2009). "Controlling fuel annealer using computational verb PID controllers". Proceedings of the 3rd International Conference on Anti-Counterfeiting, Security, and Identification in Communication. Asid'09: 417–420. ISBN 9781424438839.
- ^ Tenreiro Machado JA, et al. (2009). "Some Applications of Fractional Calculus in Engineering". Mathematical Problems in Engineering. 2010: 1–34. doi:10.1155/2010/639801. hdl:10400.22/4306.
- ^ [1] 계단식 제어의 기본 때로는 두 개의 컨트롤러가 원하는 위치에 하나의 프로세스 변수를 더 잘 유지할 수 있습니다.작성자: Vance VanDoren, PHD, 2014년 8월 17일
- ^ [2] 캐스케이드 제어의 이점 2020년 9월 22일 와트로
- ^ King, Myke (2011). Process Control: A Practical Approach. Wiley. pp. 52–78. ISBN 978-0-470-97587-9.
- ^ "Discrete PI and PID Controller Design and Analysis for Digital Implementation". Scribd.com. Retrieved 2011-04-04.
- ^ "PID process control, a "Cruise Control" example". CodeProject. 2009. Retrieved 4 November 2012.
- Bequette, B. Wayne (2006). Process Control: Modeling, Design, and Simulation. Prentice Hall PTR. ISBN 9789861544779.
추가 정보
- Liptak, Bela (1995). Instrument Engineers' Handbook: Process Control. Radnor, Pennsylvania: Chilton Book Company. pp. 20–29. ISBN 978-0-8019-8242-2.
- Tan, Kok Kiong; Wang Qing-Guo; Hang Chang Chieh (1999). Advances in PID Control. London, UK: Springer-Verlag. ISBN 978-1-85233-138-2.
- King, Myke (2010). Process Control: A Practical Approach. Chichester, UK: John Wiley & Sons Ltd. ISBN 978-0-470-97587-9.
- Van Doren, Vance J. (July 1, 2003). "Loop Tuning Fundamentals". Control Engineering.
- Sellers, David. "An Overview of Proportional plus Integral plus Derivative Control and Suggestions for Its Successful Application and Implementation" (PDF). Archived from the original (PDF) on March 7, 2007. Retrieved 2007-05-05.
- Graham, Ron; Mike McHugh (2005-10-03). "FAQ on PID controller tuning". Mike McHugh. Archived from the original on February 6, 2005. Retrieved 2009-01-05.
- Aidan O'Dwyer (2009). Handbook of PI and PID Controller Tuning Rules (PDF) (3rd ed.). Imperial College Press. ISBN 978-1-84816-242-6.
외부 링크
PID 튜토리얼
- MATLAB/Simulink 및 Python에서의 TCLab에서의 PID 제어
- 그나저나 이 P-I-D 물건들은 다 뭐야?전자 디자인 기사
- 기본 전자 구성 요소로 PID 컨트롤러를 구축하는 방법을 보여줍니다(22페이지).
- PhD가 없는 PID
- MATLAB 및 Simulink를 사용한 PID 제어
- OP 앰프가 1개인 PID
- PID 제어를 위한 검증된 방법과 베스트 프랙티스
- PID 제어 및 조정 원리
- PID 튜닝가이드: PID 컨트롤러의 이해와 조정을 위한 베스트프랙티스 접근법
- Michael Barr (2002-07-30), Introduction to Closed-Loop Control, Embedded Systems Programming, archived from the original on 2010-02-09
- Jinghua Zhong, Mechanical Engineering, Purdue University (Spring 2006). "PID Controller Tuning: A Short Tutorial" (PDF). Archived from the original (PDF) on 2015-04-21. Retrieved 2013-12-04.
{{cite web}}: CS1 maint: 여러 이름: 작성자 목록(링크) - MATLAB 탑재 P, PI, PD 및 PID 컨트롤러 소개
 연속적으로 산출하여
연속적으로 산출하여 









 각각 적분시간과 파생시간을 나타내므로 물리적인 의미를
각각 적분시간과 파생시간을 나타내므로 물리적인 의미를 




 통합 변수입니다(시간 0부터
통합 변수입니다(시간 0부터 






 PID 전송 함수,
PID 전송 함수,  플랜트 전송 함수입니다.
플랜트 전송 함수입니다.




 (를) 증가시킨 다음
(를) 증가시킨 다음 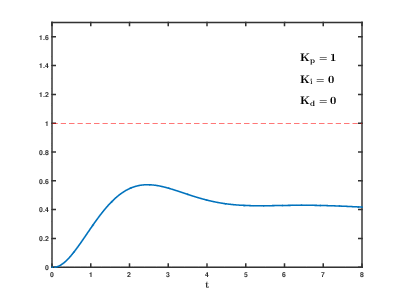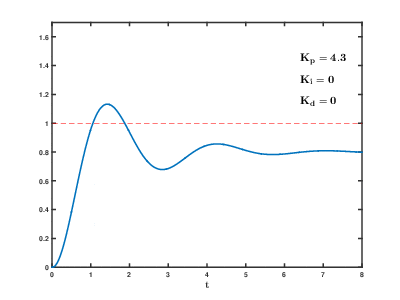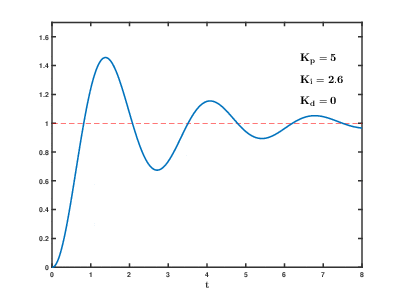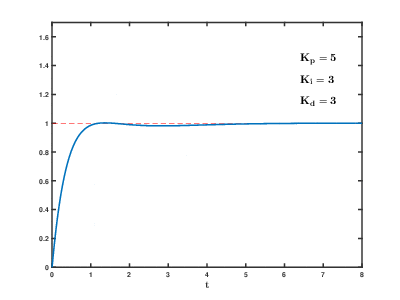

 다음과 같이 게인을 설정하는 데 사용됩니다.
다음과 같이 게인을 설정하는 데 사용됩니다.






 a는 프로세스 변수 진동의
a는 프로세스 변수 진동의 



 설정점(SP)에서 실제 측정값(PV)의 오차 또는 편차입니다.
설정점(SP)에서 실제 측정값(PV)의 오차 또는 편차입니다. 



 값을 설정하는 것은 오버슈트 감소와 안착 시간 증가 사이의 트레이드오프인 경우가 많습니다.
값을 설정하는 것은 오버슈트 감소와 안착 시간 증가 사이의 트레이드오프인 경우가 많습니다. 


 적분시간입니다.
적분시간입니다.















![{\displaystyle u(t_{k})=u(t_{k-1})+K_{p}\left[\left(1+{\dfrac {\Delta t}{T_{i}}}+{\dfrac {T_{d}}{\Delta t}}\right)e(t_{k})+\left(-1-{\dfrac {2T_{d}}{\Delta t}}\right)e(t_{k-1})+{\dfrac {T_{d}}{\Delta t}}e(t_{k-2})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e71fa41e1c58fcef6f2a3a4118577458ce29c659)
 표현되며 Kd는 s로 표현된다.액튜에이터와 측정값이 동일한 단위가 아닌 조절(예를 들어 밸브를 제어하는 모터를 이용한 온도 조절)을 할 때 단위 변환 계수로 Kp, Ki, Kd를 보정할 수 있다.Ki를 역수 형태(통합 시간)로 사용하는 것도 흥미로울 수 있다.상기의 실장에서는 I 전용 컨트롤러를 실행할 수 있습니다.이 경우 도움이 될 수 있습니다.
표현되며 Kd는 s로 표현된다.액튜에이터와 측정값이 동일한 단위가 아닌 조절(예를 들어 밸브를 제어하는 모터를 이용한 온도 조절)을 할 때 단위 변환 계수로 Kp, Ki, Kd를 보정할 수 있다.Ki를 역수 형태(통합 시간)로 사용하는 것도 흥미로울 수 있다.상기의 실장에서는 I 전용 컨트롤러를 실행할 수 있습니다.이 경우 도움이 될 수 있습니다.  로우패스 필터를 사용하여 파생 동작을 필터링하는 것입니다.
로우패스 필터를 사용하여 파생 동작을 필터링하는 것입니다. 


