응력(메트릭)

이 글은 검증을 위해 추가 인용문이 필요합니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선하는 데 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.출처 : "스트레스" 메카닉– 뉴스 · 신문 · 서적 · 학자 · JSTOR ( 2021년 8월) (이 템플릿 메시지 삭제 방법 및 삭제 타이밍에 대해 알아보기)

스트레스
편광에 의해 플라스틱 견인기 내부의 잔류응력이 드러난다.
공통 기호	σ
SI 단위	파스칼
기타 유닛	lbf/squal inch (lbf2/in ) psi
SI 기준 단위	Pa = kg µs−1−2
치수	${\displaystyle {\mathsf {L}}{-1}{\mathsf {T}}^{-2}}$

시리즈의 일부
연속체 역학
${\displaystyle J=-D{\frac {d\varphi}{displaystyle}}$ 픽의 확산 법칙
법률 보수 덩어리 모멘텀 에너지 불평등 클라우시우스듀헴(엔트로피)
고체 역학 변형 탄력성 선형의 소성 후크의 법칙 스트레스 유한 변형률 미량 변형률 호환성. 구부러지다 컨택 메카니즘 마찰의 재료고장론 파괴 역학
유체역학 유체 스태틱스 · 다이내믹스 아르키메데스의 원리 · 베르누이의 원리 나비에-스토크스 방정식 푸아세유 방정식 · 파스칼의 법칙 점성 (뉴욕 · 비뉴욕) 부력 · 믹싱 · 압력. 액체 접착 모세관 작용 크로마토그래피 응집력(화학) 표면 장력 가스 대기. 보일의 법칙 샤를의 법칙 복합가스 법칙 픽의 법칙 게이-루삭의 법칙 그레이엄의 법칙 플라즈마
레올로지 점탄성 레오메트리 레오미터 스마트 유체 전기기후학 자기 지질학 강유체
과학자 베르누이 보일 코시 찰스 오일러 픽 게이루삭 그레이엄 후크 뉴턴 경이다. 나비에 놀 파스칼 스토크스 트루즈델
v t

연속체 역학에서 응력은 물리적인 양이다.그것은 장력이나 압박과 같은 힘이 신체에 작용했을 때 발생한다.이 힘이 클수록, 그리고 이 힘이 작용하는 신체의 단면적이 작을수록, 응력은 커집니다.따라서 응력은 뉴턴/제곱미터(N/m²) 또는 파스칼(Pascal)로 전달됩니다.

응력은 연속적인 재료의 인접 입자가 서로에게 가하는 내부 힘을 나타내며, 스트레인은 재료의 변형을 측정하는 척도입니다.예를 들어, 솔리드 수직 막대가 오버헤드 웨이트를 지탱하는 경우, 막대의 각 입자는 바로 아래의 입자를 밀어냅니다.액체가 밀폐된 용기 안에 있을 때, 각각의 입자는 주변의 모든 입자에 의해 밀립니다.용기 벽과 압력 유도 표면(예: 피스톤)이 (뉴턴) 반응으로 용기 벽과 압력 유도 표면을 밀어냅니다.이러한 거시적인 힘은 실제로 분자간 힘과 분자 내 입자 간의 충돌의 최종 결과입니다.스트레스는 종종 소문자 그리스 문자 시그마(θ)로 표시됩니다.

재료 내부의 스트레인은 벌크 재료(중력 등) 또는 표면에 가해지는 압력(접촉력, 외압 또는 마찰 등)과 같은 다양한 메커니즘에 의해 발생할 수 있습니다.고체 재료의 변형(변형)은 스프링의 반력과 유사한 내부 탄성 응력을 발생시켜 재료를 원래 비변형 상태로 되돌리는 경향이 있다.액체 및 기체에서는 부피를 변경하는 변형만이 지속적인 탄성 응력을 생성합니다.그러나 시간이 지남에 따라 변형이 점차적으로 변화한다면, 유체에서도 그러한 변화에 반하는 점성 응력이 있을 것이다.탄성 응력과 점성 응력은 일반적으로 기계적 응력이라는 이름으로 결합됩니다.

변형이 무시할 수 있거나 존재하지 않는 경우에도 상당한 응력이 존재할 수 있습니다(물 흐름을 모델링할 때의 일반적인 가정).응력은 외부 힘이 없을 때 존재할 수 있습니다. 이러한 응력은 프리스트레스트 콘크리트 및 강화 유리에서 중요합니다.응력은 예를 들어 온도 또는 화학 조성의 변화 또는 외부 전자기장(압전 및 자성 재료 등)에 의해 가해질 수 있다.

기계적 응력, 변형 및 변형률 사이의 관계는 매우 복잡할 수 있지만, 수량이 충분히 작을 경우 선형 근사치가 실제로 적절할 수 있다.재료의 특정 강도 한계를 초과하는 응력은 영구 변형(플라스틱 흐름, 파괴, 캐비테이션 등)을 일으키거나 결정 구조와 화학 성분을 변화시킵니다.

공학의 일부 분과에서 스트레스라는 용어는 때때로 "내부력"의 동의어로 느슨한 의미로 사용됩니다.예를 들어 트러스 해석에서는 단면적으로 나눈 힘이 아니라 빔에 작용하는 총 견인력 또는 압축력을 나타낼 수 있다.

역사

인간은 고대부터 물질 내부의 스트레스에 대해 알고 있었다.17세기까지, 이러한 이해는 대부분 직관적이고 경험적이었지만, 이것이 복합 ^[1]활과 유리 바람과 같은 상대적으로 진보된 기술의 발전을 막지는 못했습니다.

수천 년 동안, 특히 건축가들과 건축가들은 가장 효과적인 방법으로 응력을 견디고 전달하고 분배하기 위해 ^{[citation needed]}고딕 양식의 대성당의 지붕과 같은 독창적인 장치들을 사용하여 조심스럽게 만들어진 목재 들보와 돌 블록을 조립하는 방법을 배웠다.

고대와 중세 건축가들은 기둥과 들보의 적절한 크기를 계산하기 위해 몇 가지 기하학적 방법과 간단한 공식을 개발했지만, 스트레스에 대한 과학적 이해는 17세기와 18세기에 필요한 도구가 발명된 후에야 가능해졌다: 갈릴레오 갈릴레이의 엄격한 실험 방법, 르네 데카르트의 좌표s와 해석 기하학, 그리고 뉴턴의 운동과 평형의 법칙과 무한수의 ^[2]미적분학.이 도구들로 오귀스틴-루이 코시는 균질한 ^{[citation needed]}매체에서 스트레스에 대한 최초의 엄격하고 일반적인 수학적 모델을 제공할 수 있었습니다.코치는 상상의 표면을 가로지르는 힘은 정상 벡터의 선형 함수이며, 게다가 총 ^{[citation needed]}운동량이 0인 대칭 함수여야 한다고 관찰했다.

액체 속 응력에 대한 이해는 평행 ^{[citation needed]}층류에서 마찰력에 대한 미분 공식을 제공한 뉴턴에서 시작되었습니다.

개요

정의.

응력은 ^[3]경계의 모든 방향에 대해 해당 경계의 단위 면적당 "작은" 경계를 가로지르는 힘으로 정의된다.응력은 기본적인 물리량(힘)과 순수하게 기하학적 양(면적)에서 도출되며 속도, 토크 또는 에너지와 같은 기본적인 양으로 재료의 특성이나 물리적 ^{[citation needed]}원인에 대한 명시적인 고려 없이 정량화되고 분석될 수 있다.

연속체 역학의 기본 전제에 따라, 스트레스는 거시적 개념이다.즉, 그 정의와 분석에서 고려된 입자는 구성이나 상태에서는 균질하게 취급될 수 있을 정도로 작아야 하지만, 양자 효과와 분자의 상세한 움직임을 무시할 수 있을 만큼 충분히 커야 한다.따라서, 두 입자 사이의 힘은 사실 분자 사이의 매우 많은 원자력의 평균이다; 그리고 중력과 같은 3차원 물체의 대부분을 통해 작용하는 질량, 속도, 그리고 힘과 같은 물리적인 양은 그들 ^{[4]: p.90–106} 위에 부드럽게 분포된다고 가정된다.문맥에 따라 입자가 금속 막대 ^{[citation needed]}입자나 나무 조각의 섬유와 같은 다른 미세한 특징의 평균을 낼 수 있을 정도로 충분히 크다고 가정할 수도 있습니다.

응력은 상상의 분리면 S에 걸친 재료의 인접부 사이의 견인력 F로 정의되어 S의 면적으로 나누어 정량적으로 ^{[5]: p.41–50} 표현된다.정지 상태의 유체에서 힘은 표면에 수직이며, 이는 익숙한 압력입니다.고체 또는 점성 액체의 흐름에서는 힘 F가 S에 수직이 아닐 수 있으므로 표면을 가로지르는 응력은 스칼라가 아닌 벡터량으로 간주해야 한다.또한 방향과 크기는 일반적으로 S의 방향에 따라 달라집니다.따라서 재료의 응력 상태는 (코치) 응력 텐서라고 불리는 텐서에 의해 설명되어야 한다. 이것은 표면 S의 정상 벡터 n과 S를 가로지르는 트랙션 벡터 T를 관련짓는 선형 함수이다.선택된 좌표계와 관련하여 코시 응력 텐서는 3×3 실수의 대칭 행렬로 표현될 수 있다.균질체 내에서도 응력텐서는 장소에 따라 다를 수 있으며 시간에 따라 변화할 수 있다.따라서 재료 내 응력은 일반적으로 시간 가변 ^{[citation needed]}텐서장이다.

법선응력 및 전단응력

일반적으로 입자 P가 표면 S에 걸쳐 다른 입자 Q에 가해지는 응력 T는 S에 대해 임의의 방향을 가질 수 있다.벡터 T는 표면에 수직인 수직 응력(압축 또는 장력)과 ^{[citation needed]}표면에 평행한 전단 응력의 두 가지 성분의 합으로 볼 수 있다.

표면의 법선단위벡터 n(Q에서 P를 가리키는 것)을 고정이라고 가정하면 법선성분은 도트곱 T·n이라는 단일수로 표현할 수 있다.이 숫자는 P가 Q(텐셜 스트레스)에서 "풀링"하는 경우 양수이고 P가 Q(압축 스트레스)에서 "밀어내기"하는 경우 음수입니다.전단 성분은 벡터 T - (T · n)^{[citation needed]}n이다.

단위

응력의 치수는 압력의 치수이며, 따라서 그 좌표는 일반적으로 압력과 같은 단위로 측정됩니다. 즉, 국제 시스템의 파스칼(Pa, 평방미터당 뉴턴) 또는 제국 시스템의 평방인치당 파운드(psi)입니다.기계적 응력이 100만 파스칼을 훌쩍 넘기 때문에 메가파스칼을 뜻하는 MPa는 일반적인 ^{[citation needed]}응력 단위다.

원인과 결과

물질 본체의 응력은 외부 영향 및 내부 물리적 과정을 포함한 여러 물리적 원인에 의해 발생할 수 있습니다.이러한 물질 중 일부(중력, 온도 및 위상 변화, 전자기장 등)는 소재의 대부분에 작용하며 위치와 시간에 따라 지속적으로 변화합니다.다른 작용제(외부 하중 및 마찰력, 주변 압력 및 접촉력 등)는 응력과 힘을 발생시켜 특정 표면, 선 또는 점에 집중시킬 수 있습니다.또한 매우 짧은 시간 간격(충돌로 인한 충격 등)에도 집중시킬 수 있습니다.활성물에서는 현미경 입자의 자기 추진이 거시적 응력 프로파일을 ^[7]생성한다.일반적으로 물체의 응력분포는 공간 및 시간의 공간적 연속함수로 표현된다.

반대로 응력은 보통 재료에 대한 다양한 영향과 상관관계가 있으며 이중 굴절, 편광 및 투과성과 같은 물리적 특성의 변화를 포함할 수 있다.외부 작용제에 의한 응력 작용은 검출하기에는 너무 작더라도 일반적으로 재료에 약간의 변형(변형)을 일으킨다.고체재료에서 이러한 변형은 신장스프링의 반력과 유사한 내부탄성응력을 발생시켜 재료를 원래의 미성형 상태로 되돌리는 경향이 있다.유체 물질(액체, 가스 및 플라스마)은 정의상 부피가 변화하는 변형에만 반대할 수 있습니다.그러나 변형이 시간에 따라 변화하고 있는 경우, 유체에서도 일반적으로 약간의 점성 응력이 존재하여 이러한 변화에 반대합니다.이러한 응력은 본질적으로 전단 또는 정상일 수 있습니다.유체 중 전단 응력의 분자 기원은 점도에 관한 기사에서 주어진다.샤르마(2019)^[8]에서도 정상 점성 응력에 대해 동일한 것을 확인할 수 있다.

변형과 변형 변화 속도를 포함한 응력과 그 영향 및 원인 사이의 관계는 매우 복잡할 수 있다(단, 수량이 충분히 작은 경우 실제로 선형 근사치가 적절할 수 있다).재료의 특정 강도 한계를 초과하는 응력은 영구 변형(플라스틱 흐름, 파괴, 캐비테이션 등)을 일으키거나 결정 구조와 화학 성분을 ^{[citation needed]}변화시킵니다.

단순 스트레스

경우에 따라서는, 물체내의 응력은, 단일의 숫자 또는 단일의 벡터(숫자와 방향)에 의해서 적절히 설명될 수 있습니다.엔지니어링 설계에서 흔히 볼 수 있는 세 가지 간단한 응력 상황은 단축 정규 응력, 단순 전단 응력 및 등방성 정규 ^[9]응력입니다.

단축 정상 응력

단순한 응력 패턴의 일반적인 상황은 균일한 재료와 단면을 가진 스트레이트 로드가 축을 따라 $진도{\displaystyle }$ $F(\displaystyle$ F$)$의 반대 힘에 의해 장력을 받는 경우입니다.시스템이 평형 상태에 있고 시간에 따라 변화하지 않고 바의 중량을 무시할 수 있는 경우, 바의 각 횡단부를 통해 상단부는 동일한 힘, 전체 단면적 A를 통해 연속성을 갖는 하부를 잡아당겨야 한다.따라서 수평면에 걸친 막대 전체의 응력 θ는 단순히 하나의 숫자 θ로 표현할 수 있으며, 이러한 힘의 크기 F와 단면적 A로 계산된다.

한편, 막대가 축에 평행하게 길이를 따라 절단되는 상상을 하면 절단된 ^{[citation needed]}두 절반 사이에 힘이 가해지지 않는다(따라서 응력이 가해지지 않는다).

이러한 유형의 스트레스는 (단순) 정상 응력 또는 단축 응력, 특히 (단축, 단순 등) 인장 ^[9]응력이라고 할 수 있습니다.하중이 스트레칭이 아닌 바에 대한 압축일 경우, 힘 F와 응력$\delta {\displaystyle }$(\$displaystyle \sigma)$의 변화부호를 제외하고 해석은 동일하며, 그 응력을 압축응력이라고 한다.

이 분석에서는 응력이 전체 단면에 고르게 분포되어 있다고 가정합니다.실제로는 막대가 끝에 어떻게 부착되어 있고 어떻게 제조되었는지에 따라 이 가정은 유효하지 않을 수 있습니다.이 경우 값$\delta {\displaystyle }$ {$style \display }$ =$$ F/A는 엔지니어링 스트레스 또는 공칭 스트레스라고 하는 평균 응력만 됩니다.그러나 막대 길이 L이 직경 D의 여러 배이고 총 결점이나 내재 응력이 없는 경우 응력은 양 끝에서 D의 몇 배보다 큰 단면에 걸쳐 균일하게 분포한다고 가정할 수 있습니다(이 관측치를 Saint-Venant의 ^[citation needed]원리라고 합니다).

정상적인 응력은 축방향 장력과 압축 이외에도 많은 다른 상황에서 발생합니다.균일하고 대칭적인 단면을 가진 탄성 바가 대칭 평면 중 하나에서 구부러진 경우, 결과 굽힘 응력은 여전히 정상(단면에 수직)이지만 단면에 따라 변화합니다. 즉, 외부 부분은 인장 응력을 받는 반면 내부 부분은 압축됩니다.정상 응력의 또 다른 변형은 가압된 ^{[citation needed]}유체로 채워진 원통형 파이프나 용기의 벽에서 발생하는 후프 응력입니다.

단순 전단 응력

또 다른 간단한 유형의 응력은 접착제나 고무와 같은 균일하게 두꺼운 탄성 재료의 층이 층과 평행한 힘에 의해 반대 방향으로 당기는 두 개의 단단한 몸체에 단단히 부착되어 있거나 가위 같은 도구의 턱으로 절단되는 부드러운 금속 막대의 일부에 의해 발생합니다.F를 그 힘의 크기, M을 그 층의 중간 평면으로 합니다.통상적인 응력의 경우와 마찬가지로 M의 한쪽 층의 부분은 F의 동일한 힘으로 다른 부분을 당길 필요가 있다.힘의 방향을 알고 있다고 가정할 때, M을 가로지르는 응력은 단순히 힘의 크기 F와 단면적 A로 계산되는 단일 숫자$\delta {\displaystyle }$(\$displaystyle\tau)$로 간단히 표현할 수 있다.

그러나 일반 응력과 달리 이 단순 전단 응력은 고려된 단면에 ^[9]수직이 아닌 평행으로 향한다.층에 수직인 평면 S에 대해 S를 가로지르는 순 내부력, 즉 응력은 0이 됩니다.

축방향으로 하중을 받는 막대의 경우와 마찬가지로 실제로는 전단 응력이 층 전체에 균일하게 분포되지 않을 수 있습니다. 따라서 F/A 비율은 평균("공칭", "공학") 응력일 뿐입니다.그러나 그러한 평균은 종종 실무적인 ^{[10]: p.292} 목적을 위해 충분하다.샤프트 등의 원통형 막대가 단부에 반대 토크를 가해도 전단 응력이 관찰된다.이 경우 각 단면의 전단응력은 단면과 평행하지만 축에 대해 접선방향으로 배치되며 축으로부터의 거리에 따라 증가한다.웹이 엔드 플레이트("플랜지")^{[citation needed]}를 구속하기 때문에 굽힘 하중을 받는 I빔의 중간 플레이트("웹")에서 상당한 전단 응력이 발생합니다.

등방 응력

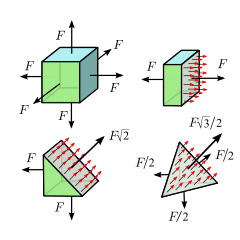
또 다른 간단한 유형의 응력은 재료 본체가 모든 방향으로 동일한 압축 또는 장력을 받을 때 발생합니다.예를 들어, 액체 또는 가스의 정지된 부분에서는, 일부 용기에 밀폐되거나 더 큰 유체 덩어리의 일부로, 또는 동일한 수직 힘에 의해 6개 면 모두에서 눌리거나 당겨지는 탄성 재료의 큐브 내부가 해당됩니다. 단, 두 경우 모두 재료가 내장 응력이 없는 균질한 경우, 그리고중력과 기타 외부 힘의 영향을 ^{[citation needed]}무시할 수 있습니다.

이러한 상황에서 가상 내부 표면의 응력은 크기가 같으며 항상 표면의 방향과 독립적으로 표면에 수직 방향으로 향합니다.이러한 유형의 응력은 등방성 정상 또는 그냥 등방성이라고 할 수 있습니다. 압축성이면 정수압 또는 그냥 압력이라고 합니다.기체는 정의상 인장응력을 견딜 수 없지만, 일부 액체는 상황에 따라 놀랄 만큼 많은 양의 등방성 인장응력을 견딜 수 있다.'Z튜브'^{[citation needed]} 참조.

실린더 응력

휠, 액슬, 파이프 및 필러와 같이 회전 대칭이 있는 부품은 엔지니어링에서 매우 일반적입니다.이러한 부품에서 발생하는 응력 패턴은 회전 대칭 또는 원통 대칭을 갖는 경우가 많습니다.이러한 실린더 응력의 분석은 영역 및/또는 응력 ^{[citation needed]}텐서의 치수를 줄이기 위해 대칭성을 이용할 수 있다.

일반응력

종종, 기계적인 신체는 동시에 두 가지 이상의 스트레스를 경험합니다; 이것은 복합 스트레스라고 불립니다.정상응력 및 전단응력에서 응력의 크기는 $특정방향{\displaystyle }$ d$\displaystyle$ d$\backslash$에 수직인 표면에서는 최대이고 d$\displaystyle$ d$\backslash$에 평행한 표면에서는 0이다. 전단응력이 특정방향에 수직인 표면에서만 0일 경우 응력 i는s는 이축이라고 불리며, 두 개의 정상 또는 전단 응력의 합으로 볼 수 있습니다.가장 일반적인 경우, 삼축 응력이라 불리는 응력은 모든 표면 ^{[citation needed]}요소에서 0이 아닙니다.

코시 응력 텐서

결합된 응력은 단일 벡터로 설명할 수 없습니다.소재가 물체의 부피 전체에 걸쳐 동일한 방식으로 응력을 받는다고 해도,^{[citation needed]} 상상 표면의 응력은 중요하지 않은 방식으로 해당 표면의 방향에 따라 달라집니다.

그러나 Cauchy는 표면을 가로지르는 응력 $벡터{\displaystyle }$T(\$displaystyle$ T$)$는 항상 표면에 수직인 단위 길이 $벡터{\displaystyle }$ n$(\displaystyle$ n$)$의 선형 함수임을 관찰했다.$즉{\displaystyle }$, T ${\displaystyle =\sigma \mathit{}}$ (${\displaystyle n}$ )$${ $displaystyle$$$T = bold $symbol${ n }$$$（$ $n$） 。$이$ 함수는 $다음$과 같습니다$.$

${\displaystyle {\boldsymbol u+\display v}=\alpha {\boldsymbol u}(u)+\display style {\boldsymbol }(v)}$

$벡터{\displaystyle }$u, ${\displaystyle v}${\$displaystyle u$,v$}$ 및 실수$$$$α, β, ${\displaystyle \alpha$,\$beta{\displaystyle }$$\}$에 대한 $함수{\displaystyle \mathit{}}$( {\$displaystyle${\$sigma }$는 현재 (코치) 응력 텐서로 불리는 균등하게 응력된 물체의 응력 상태를 완전히 나타냅니다.개별성은 텐서(tensor)라고 불리며, 재료의 "tensions"(스트레스)를 설명하기 위한 코시의 원래 용도를 반영한다.텐서 미적분학에서$\delta {\displaystyle \mathit{}}$(\$displaystyle\boldsymbol\sigma })$는 유형(0,2)의 ^{[citation needed]}2차 텐서로 분류된다.

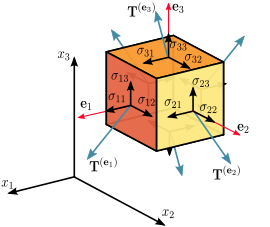
벡터 사이의 다른 선형 지도와 마찬가지로, 응력 텐서는 선택된 데카르트 좌표계에서 실수의 3×3 행렬에 의해 표현될 수 있다.좌표의 $번호$가 ${\displaystyle {x\mathrm{}}_{}}$1, ${\displaystyle {x\mathrm{}}_{}}$2, ${\displaystyle {x\mathrm{}}_{}}$ 3$({$})인지$$ $또는{\displaystyle }$ x${\displaystyle ,}$ ${\displaystyle y,}$(\$display x,y,z$인지에 따라 매트릭스는 다음과 같이 기술될 수 있습니다.

또는 ${\displaystyle {좌표}_{}}$가 n 1,${\displaystyle {}_{}{}_{}}$ ${\displaystyle {}_{}}$,${\displaystyle {}_{}{n\mathrm{}}_{}}$3 {$displaystyle n_1, n_2$, $n_n_{2}, n_3}$인 정규 ${\displaystyle }$n$($공변 - "행; 수평" - 벡터)을 갖는 표면에 걸친 $응력$ 벡터 T$=$ ${\displaystyle (}$($n$)는 $산물{\displaystyle =}$ ${\displaystyle \mathrm{행렬}}$이다.$ot${\$boldsymbol {sigma$}}($$상위 지수의 T는 전위이고, 그 결과 공변량(행) 벡터를 얻을 수 있다)(코시 스트레스 텐서를 살펴본다), 즉,

$(\displaystyle \ bmatrix \T_{1}&T_{2}&T_{3}\end{bmatrix}="begin{bmatrix}n_{1}&n_{2}&n_{3}\end{bmatrix}\cdot {11}&\cdot {bmatrix}\cdot {11}&\cdot {bmatrix}_{21}>\cdline_{bmatrix}_{bmatrix}_{batrix}_{b}\cd}_{batrix}\cd}_{b}\cd$

T$${\$displaystyle$ T$}$와$$n {\$displaystyle$ n$}$ $사이$의 선형 관계는 선형 운동량 보존의 기본 법칙과 힘의 정적 균형에서 비롯되며, 따라서 수학적으로 모든 재료와 응력 상황에 대해 정확합니다.물질의 모든 점에서 코시 응력 텐서의 성분은 평형 방정식(제로 가속에 대한 코시의 운동 방정식)을 충족합니다.또한 각운동량 보존원칙은 응력텐서가 대칭임을 의미한다. 즉, ${\displaystyle {12}_{}}$ 12 ${\displaystyle {}_{}}$ ${\$ ${\displaystyle {21}_{}}${ $displaystyle$ \$displaystyle$$_$ { $12$ = \$display$ ${\displaystyle {\mathrm{style}}_{}}$ _ { 13 } = \ display style _ { 13 } = \ $display$ _ { $31$$$} = { $31}$ $23$ 23 ${\displaystyle {}_{}}$ $=$ { $displaystyledisplay$ style \ display style$_$ { 23 } } { $32$ } { 32$}$ }$$} . 32 。임의의 지점과 순간에 매체의 ss 상태는 9가 아닌 6개의 독립적인 파라미터로만 지정할 수 있습니다.이것들은 쓰여질 수 있다.

${\displaystyle {bmatrix}\displaystyle _{xy}&\display_{xy}&\display_{xy}&\display_{yz}&\display_{xy}&\display_{bmatrix}}$

여기서 요소 ${\displaystyle x_{}}$x , $y$${\displaystyle {}_{}}$y , $z$z \$displaystyle \displays _{$${\displaystyle x_{}}$}, \$displaystyle$ _{${\displaystyle y_{}}$ z \displaystyle$_{xy},$ \$displaystyle$ _{$xz},$ \displaystyle _${xz},$ \$displays$ _${$yz}}^{[citation needed]}는$$$$ 직교 응력이라고 합니다.

좌표 변경

코시 응력 텐서는 좌표계의 변화 하에서 텐서 변환 법칙을 따릅니다.이 변환 법칙을 그래픽으로 나타낸 것이 Mohr의 응력 분포 ^{[citation needed]}원입니다.

대칭적인 3×${\displaystyle {}_{}}$ 실행렬로서 응력텐서$δ(\$$displaystyle\$$boldsymbol\sigma})$는 상호 직교하는$$3개의 단위길이 ${\displaystyle {고유벡터\mathrm{}}_{}{}_{}{e1\mathrm{}}_{}}$, $e2, e_{3$}}와 $3개$의 $실고유치{\displaystyle {}_{}}$,$$$δ3_lambda{1},$ lam2}를 가진다$.$${\displaystyle {e-i}_{}}$ $=$ ${\displaystyle {e-i-i}_{}}$를$표시$합니다.\displaystyle {\$boldsymbol {\i$} =\$displayda$ _${i} e_{i$ 。$따라서{\displaystyle {}_{}}$ 축 ${\displaystyle {e1\mathrm{}}_{}}$ $($ 스타일 e_{1}, e_{2$}, e_{3$의 좌표계에서 응력텐서는 대각행렬이며, $($ 스타일 $\lambda$ _${1},\lambda _{2$},\$lambda _3}})$의 세 가지 정규 성분만을 ${\displaystyle {가진다\mathrm{}}_{}}$.3개의 고유값이 같으면 응력은 등방성 압축 또는 장력이며, 항상 어떤 표면에 수직이며 전단 응력은 없으며, 텐서는 어떤 좌표 ^{[citation needed]}프레임에서도 대각 행렬입니다.

텐서장으로서의 응력

일반적으로 응력은 물질 전체에 균일하게 분포되지 않으며 시간에 따라 달라질 수 있습니다.따라서 응력 텐서는 각 점 및 각 모멘트에 대해 정의되어야 하며, 그 점을 둘러싼 매체의 극소 입자를 고려하여 해당 입자의 평균 응력을 해당 ^{[citation needed]}점의 응력으로 간주해야 합니다.

얇은 판의 응력

인공 물체는 절단, 드릴링, 완만한 굽힘 및 가장자리를 따라 용접하는 것과 같이 기본적으로 2차원 특성을 바꾸지 않는 작업에 의해 다양한 재료의 스톡 플레이트로 만들어지는 경우가 많습니다.이러한 물체의 응력 설명은 해당 부품을 3차원 ^{[citation needed]}물체가 아닌 2차원 표면으로 모델링함으로써 단순화할 수 있다.

이러한 관점에서, "입자"를 플레이트 표면의 극소 패치라고 재정의하면 인접한 입자 사이의 경계가 극소 선 요소가 된다. 둘 다 플레이트에 대해 법선인 3차원으로 암묵적으로 연장된다(직선).그런 다음 "스트레스"는 공통 선 요소를 가로지르는 인접한 두 "입자" 사이의 내부 힘을 해당 선의 길이로 나눈 측정값으로 재정의된다.응력 텐서의 일부 구성요소는 무시할 수 있지만, 입자가 3차원에서 무한소형이 아니기 때문에 입자가 이웃에 가해지는 토크를 더 이상 무시할 수 없습니다.이 토크는 플레이트의 곡률을 변화시키는 경향이 있는 굽힘 응력으로 모델링됩니다.그러나 이러한 단순화는 용접부, 급커브 및 주름(곡률 반경이 ^{[citation needed]}판 두께와 맞먹는 경우)에서는 유지되지 않을 수 있습니다.

얇은 보의 응력

응력 분석은 적당한 굽힘과 비틀림을 받는 균일한(또는 부드럽게 변화하는) 구성과 단면의 얇은 막대, 빔 또는 와이어에 대해서도 상당히 단순화할 수 있다.이러한 물체에 대해서는 바의 축에 수직인 단면만을 고려하여 "입자"를 그러한 두 단면 사이에 최소 길이의 와이어로 재정의할 수 있다.그런 다음 일반 응력은 스칼라(막대의 장력 또는 압축)로 감소하지만, 굽힘 응력(막대의 곡률을 축에 수직인 방향으로 변경하려는 것)과 비틀림 응력(막대의 ^{[citation needed]}축을 중심으로 비틀림 또는 비틀림 해제하려는 것)도 고려해야 합니다.

스트레스에 대한 기타 설명

코시 응력 텐서는 대부분의 경우 응력 분포의 차이를 무시할 수 있는 작은 변형을 경험하는 재료의 응력 분석에 사용된다.유한 변형이라고도 불리는 대규모 변형에는 제1 및 제2의 피올라-키르호프 응력 텐서, 비오트 응력 텐서 및 키르호프 응력 텐서와 같은 다른 응력 측정이 필요하다.^{[citation needed]}

고체, 액체, 기체에는 응력장이 있습니다.정적 유체는 정상 응력을 지원하지만 전단 응력 하에서 흐릅니다.비스코스 유체를 움직이면 전단 응력(동압)을 지탱할 수 있습니다.고형물은 전단 응력과 통상 응력을 모두 지탱할 수 있으며, 연성 재료는 전단 응력 하에서 파괴되고 메짐성 재료는 통상 응력 하에서 파괴된다.모든 재료는 응력 관련 특성에서 온도에 따라 차이가 있으며, 비뉴턴 재료는 비율에 따라 ^{[citation needed]}차이가 있습니다.

응력 분석

응력 분석은 고체 물체에서 내부 힘의 내부 분포를 결정하는 것을 다루는 응용 물리학의 한 분야입니다.이는 규정된 또는 예상 하중 하에서 터널, 댐, 기계 부품 및 구조 프레임과 같은 구조물의 연구와 설계에 필수적인 도구이다.많은 다른 분야들에서도 중요하다; 예를 들어, 지질학에서는 판구조학, 벌컨주의, 눈사태와 같은 현상을 연구하는 것; 그리고 생물학에서는,^{[citation needed]} 생물들의 해부학을 이해하는 것이 중요하다.

목표와 전제 조건

응력 분석은 일반적으로 거시적 정적 평형에 있다고 가정할 수 있는 물체 및 구조와 관련이 있다.뉴턴의 운동 법칙에 따르면, 그러한 시스템에 가해지는 모든 외부 힘은 내부 반력에 의해 균형을 이루어야 하는데, 내부 ^{[11]: p.97} 반력은 거의 항상 인접한 입자 사이의 표면 접촉력이다. 즉,^[5] 응력이다.모든 입자가 평형을 이루어야 하기 때문에, 이 반응 스트레스는 일반적으로 입자에서 입자로 전파되어 ^{[citation needed]}몸 전체에 스트레스 분포를 형성합니다.

응력 분석의 일반적인 문제는 시스템에 작용하는 외부 힘을 고려하여 이러한 내부 응력을 결정하는 것입니다.2차원 혹은 한 행, 또는 한 지점에서 이상 행동한다고 생각한다 후자는 아마도 몸 힘, 재료의 속에서 그런 행동( 같은 중력 또는 자기 매력),[12]:p.42–81 또는 농축 부하( 같은 마찰 사이의 차축과 베어링, 또는 살이 기차 바퀴에 레일).[표창 필요한]

응력 분석에서는 일반적으로 힘의 물리적 원인이나 재료의 정확한 특성을 무시한다.대신, 응력은 알려진 구성 ^[13]방정식에 의한 재료의 변형(및 비정적 문제에서는 변형 비율)과 관련이 있다고 가정한다.

방법들

응력 분석은 실제 아티팩트 또는 스케일 모델에 하중을 가하고 사용 가능한 몇 가지 방법 중 하나를 사용하여 결과 응력을 측정함으로써 실험적으로 수행될 수 있다.이 접근방식은 안전인증 및 모니터링에 자주 사용됩니다.그러나 대부분의 응력 분석은 특히 설계 중에 수학적 방법으로 이루어집니다.기본적인 응력 분석 문제는 연속체에 대한 오일러의 운동 방정식과 적절한 구성 방정식과 함께 오일러-코치 응력 원리에 의해 공식화될 수 있습니다.따라서 결정되어야 할 미지의 함수로서 응력 텐서장과 변형 텐서장을 포함하는 편미분 방정식의 시스템을 얻을 수 있다.외부 체력은 미분 방정식에서 독립("오른쪽") 항으로 나타나는 반면, 집중력은 경계 조건으로 나타납니다.따라서 기본 응력 분석 문제는 경계 값 문제입니다.^{[citation needed]}

탄성 구조에 대한 응력 분석은 탄성 이론과 극소 변형률 이론에 기초한다.가해진 하중이 영구적인 변형을 일으킬 경우, 관련된 물리적 과정(플라스틱 흐름, 파괴, 위상 변화 등)을 설명할 수 있는 보다 복잡한 구성 방정식을 사용해야 합니다.^{[citation needed]}

그래서 우리가 기대했던 스트레스를 선형 탄성(훅의 법칙의 지속적인 미디어에 대한 일반화)의 음역 안이;이 있는 최대, 변형 내부 응력에 의해 야기된 선형적으로 그들에게 관련된 그러나 인공 구조 보통 설계된다.이러한 경우 변형력 텐서를 규정하는 미분 방정식이 들고, 그 문제를 훨씬 더 쉬워 지선형이다.한가지 예로 부하, 임의 지점에서의 스트레스는 선형 함수도.작은 충분한 스트레스 들자면, 비선형 시스템은 보통 선형 것을 가정할 수 있다.[표창 필요한]

때 하중의 물리적 치수와 분포는 구조 한개 또는 2차원으로 처리될 수 있는 스트레스는 분석 간단합니다.트러스 구조의 분석에서, 예를 들어, 스트레스 분야와 단축의 각 멤버에 동일하게 가정할 수 있다.그리고 그 미분 방정식 방정식 유한하게 많은 알려지지 않은 사람들과(보통 선형)유한한 집합을 줄여 준다.다른 맥락에서 보면 하나는 2차원 한 그리고/혹은 교체 단축 tension/compression, 단순 전단, 등과 같은 더 단순한 모델이 3차원 문제는 일반적인 응력과 변형 tensors을 줄일 수 있을 것[표창 필요한]

여전히 평면이나 3차원적인 경우를 누군가는 편미분 방정식 문제를 해결해야 한다.는 기하학, 구성 관리 그리고 경계 조건은 충분히 간단한 미분 방정식이나closed-form 분석 해결책 얻을 수 있다.그렇지 않으면 하나는 일반적으로 유한 요소 법, 유한 차분법, 경계 요소 법과 같은 수치 근사치에 의지해야 한다.[표창 필요한]

스트레스의 대체 척도

다른 유용한 스트레스 대책이 첫번째와 두번째 Piola–Kirchhoff 스트레스 tensors, 비오 변형력 텐서, 그리고 Kirchhoff변형력 텐서를 포함한다.

피올라-키르호프 응력 텐서

이 섹션은 '피올라-키르호프 스트레스 텐서'라는 제목의 다른 기사로 분할할 것을 제안했다. (토론) (2021년 2월)

유한 변형의 경우, 피올라-키르호프 응력 텐서는 기준 구성에 상대적인 응력을 표현한다.이는 현재 구성에 상대적인 응력을 표현하는 코시 응력 텐서와 대조적이다.미세한 변형과 회전의 경우 코치와 피올라-키르호프 텐서는 동일합니다.^{[citation needed]}

코시 응력 텐서$${\({$displaystyle\boldsymbol\sigma}})$는 현재 구성에서 응력을 관련짓는 반면 변형 구배와 변형 텐서는 기준 구성과 관련지어 기술됩니다. 따라서 재료 상태를 설명하는 모든 텐서가 기준 구성 또는 현재 구성에 있는 것은 아닙니다.음이온. 기준 또는 전류 구성에 응력, 변형 및 변형을 기술하면 구성 모델을 정의하기가 더 쉬워질 것이다(예를 들어, 변형 변형 변형 텐서는 불변인 반면 코시 응력 텐서는 순수한 회전으로 변형된다). 따라서 변형 텐서는 변이를 관련짓는 구성 모델을 정의하는 데 문제를 일으킨다.g 텐서(순수 회전 중 불변의 관점에서), 정의에 따라 구성 모델은 순수 회전과 불변해야 한다.)첫 번째 Piola-Kirchhoff 응력 텐서 $(\$는 이 문제에 대한 하나의 가능한 해결책입니다.텐서 패밀리를 정의합니다.텐서 패밀리는 현재 ^{[citation needed]}상태 또는 기준 상태의 바디 구성을 나타냅니다.

첫 번째 피올라-키르호프 응력 텐서인 $(\displaystyle {\boldsymbol${P$$})는 현재("공간") 구성의 힘과 기준("물질")^{[citation needed]} 구성의 영역을 연관시킵니다.

${{displaystyle {P}}=J~{\boldsymbol {F}}~{\boldsymbol {F}^{-T}~}$

$여기$서 F$(\${\$boldsymbol {F})$는 변형 구배, J$=$F(\$displaystyle$ J=\$det {\boldsymbol {F})$는 야코비안 행렬식입니다.^{[citation needed]}

직교 정규 기준과 관련하여 첫 번째 피올라-키르호프 응력은 다음과 같이 주어진다.

${\displaystyle P_{iL}=J~\sigma _{ik}~F_{Lk}=J~\sigma _{ik}~{\displayac {\partial x_{k}}~,\!}$

다른 좌표계를 관련시키기 때문에 첫 번째 피올라-키르호프 응력은 2점 텐서이다.일반적으로 대칭이 아닙니다.첫 번째 피올라-키르호프 스트레스는 엔지니어링 스트레스의 1D 개념을 ^{[citation needed]}3D로 일반화한 것입니다.

재료가 응력 상태의 변화 없이 회전하는 경우(강성 회전), 첫 번째 피올라-키르호프 응력 텐서의 구성요소는 재료 ^{[citation needed]}방향에 따라 달라진다.

첫 번째 피올라-키르호프 응력은 변형 ^{[citation needed]}구배와 에너지 공역이다.

제2피올라-키르호프 응력 텐서

첫 번째 피올라-키르호프 응력은 현재 구성의 힘을 기준 구성의 영역에 관련짓는 반면, 두 번째 피올라-키르호프 응력 $텐서{\displaystyle \mathit{}}$S(\$displaystyle\boldsymbol {S}})$는 기준 구성의 힘을 기준 구성의 영역에 관련짓습니다.기준 구성의 힘은 기준 구성의 수직 영역과 힘 방향 사이의 상대적 관계를 보존하는 매핑을 통해 얻어집니다.

${\displaystyle {S}=J~{\boldsymbol {F}}{-1}\cdot {\boldsymbol {F}}\cdot {\boldsymbol {F}^-T}~}$

직교 정규 기법에 관한 지수 표기법에서,

${\displaystyle S_{IL}=J~F_{Ik}^{-1}~F_{Lm}^{-1}~\sigma_{km}=J~{\cfrac {\cfrac X_{\cfrac}I}}{\partial x_{k}}~{\cfrac {\partial x_{L}}{\partial x_{m}}~\sigma _{km}\!,\!}$

1점 텐서인 이 텐서는 ^{[citation needed]}대칭이다.

재료가 응력 상태의 변화 없이 회전하는 경우(강성 회전), 두 번째 피올라-키르호프 응력 텐서의 구성요소는 재료 방향에 ^{[citation needed]}관계없이 일정하게 유지됩니다.

두 번째 피올라-키르호프 응력 텐서는 그린-라그랑주 유한 변형 ^{[citation needed]}텐서와 에너지 공역이다.

「 」를 참조해 주세요.

시리즈의 일부
연속체 역학
${\displaystyle J=-D{\frac {d\varphi}{displaystyle}}$ 픽의 확산 법칙
법률 보수 덩어리 모멘텀 에너지 불평등 클라우시우스듀헴(엔트로피)
고체 역학 변형 탄력성 선형의 소성 후크의 법칙 스트레스 유한 변형률 미량 변형률 호환성. 구부러지다 컨택 메카니즘 마찰의 재료고장론 파괴 역학
유체역학 유체 스태틱스 · 다이내믹스 아르키메데스의 원리 · 베르누이의 원리 나비에-스토크스 방정식 푸아세유 방정식 · 파스칼의 법칙 점성 (뉴욕 · 비뉴욕) 부력 · 믹싱 · 압력. 액체 접착 모세관 작용 크로마토그래피 응집력(화학) 표면 장력 가스 대기. 보일의 법칙 샤를의 법칙 복합가스 법칙 픽의 법칙 게이-루삭의 법칙 그레이엄의 법칙 플라즈마
레올로지 점탄성 레오메트리 레오미터 스마트 유체 전기기후학 자기 지질학 강유체
과학자 베르누이 보일 코시 찰스 오일러 픽 게이루삭 그레이엄 후크 뉴턴 경이다. 나비에 놀 파스칼 스토크스 트루즈델
v t

켤레 변수 열역학의

압력. 용량 (스트레스) (스트레인) 온도 엔트로피 화학 퍼텐셜 파티클 번호

레퍼런스

추가 정보