점군

홍콩 지역 깃발의 Bauhinia Blakeana 꽃은 C 대칭을 가지며5, 각 꽃잎의 별은 D 대칭을 가집니다5.

음양 기호는 반전된 색상과 함께 기하학의 C 대칭을 가진다2.

기하학에서 점군(point group)은 공통적으로 고정된 점을 갖는 대칭 연산의 수학적 그룹이다.유클리드 공간의 좌표 원점은 일반적으로 고정점으로 간주되며, 차원 d의 모든 점군은 직교군 O(d)의 부분군이 된다.점 그룹은 기하학적 도형과 분자와 같은 물리적 객체의 대칭을 설명하는 데 사용됩니다.

각 점 그룹은 y = Mx에 따라 점 x를 점 y로 변환하는 직교 행렬 M의 집합으로 나타낼 수 있습니다. 점 그룹의 각 요소는 회전(M = 1의 등가)이거나 반사 또는 부적절한 회전(M = -1의 등가)입니다.

결정의 기하학적 대칭은 공간 그룹에 의해 설명되며, 공간 그룹은 변환을 허용하고 점 그룹을 하위 그룹으로 포함합니다.두 개 이상의 차원에 있는 이산 점군은 무한 패밀리로 나오지만, 결정학적 제한 정리와 비버바흐의 이론 중 하나에 따르면, 각 차원은 그 차원의 수를 가진 격자 또는 격자에 대칭인 유한한 수의 점군만 가지고 있습니다.이것들은 결정학적 점군입니다.

카이랄 및 아치랄 점 그룹, 반사 그룹

점 그룹은 키랄(또는 완전히 회전) 그룹과 아키랄 ^[1]그룹으로 분류할 수 있습니다.카이랄 그룹은 특수 직교 그룹 SO(d)의 부분군입니다. 즉, 방향 보존 직교 변환, 즉 행렬식 +1의 변환만 포함합니다.아키랄 그룹에는 결정식 -1의 변환도 포함되어 있습니다.아키랄군에서 배향 보존 변환은 지수 2의 (키랄) 서브그룹을 형성한다.

유한 콕서터 그룹 또는 반사 그룹은 동일한 지점을 통과하는 반사 거울 세트에 의해 순수하게 생성된 점 그룹이다.랭크 n의 콕서터 그룹은 n개의 거울을 가지며 콕서터-딘킨 다이어그램으로 나타난다.콕서터 표기법은 회전 및 기타 준대칭 점 그룹에 대한 마크업 기호가 있는 콕서터 다이어그램과 동등한 괄호 표기법을 제공합니다.반사 그룹은 반드시 achiral입니다(ID 요소만 포함하는 사소한 그룹은 제외).

점 그룹 리스트

일차원

1차원 점 그룹은 아이덴티티 그룹과 반사 그룹 두 개뿐입니다.

그룹.	콕서터	콕서터 다이어그램	주문	묘사
C1	[ ]+		1	신원
D1	[ ]		2	반사 그룹

2차원

2차원의 점 그룹(로제트 그룹이라고도 함)

두 개의 무한 패밀리가 있습니다.

1. n배 회전 그룹의 순환 그룹_n C
2. n배 회전 및 반사 그룹의 이면체 군 D_n

결정학적 제한 정리를 적용하면 n이 두 계열의 값 1, 2, 3, 4, 6으로 제한되어 10개의 그룹이 생성됩니다.

그룹.	국제	오르비폴드	콕서터	주문	묘사
Cn	n	n•	[n]+	n	주기: n배 회전.추상군n Z, 덧셈 모듈로n 아래의 정수군입니다.
Dn.	nm	*n•	[n]	2n	이면체: 반사가 있는 순환형.추상군n Dih, 이면체군.

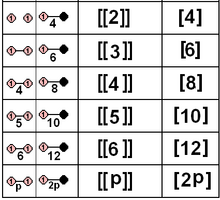
1개 또는 2개의 거울로 정의되는 순수 반사 점 그룹의 부분 집합은 또한 해당 콕서터 그룹과 관련 폴리곤에 의해 지정될 수 있다.여기에는 5개의 결정학적 그룹이 포함됩니다.반사 그룹의 대칭은 동형사상에 의해 두 배가 될 수 있으며, 이등분 거울에 의해 두 개의 거울이 서로 매핑되어 대칭 순서가 두 배가 됩니다.

사색적인						회전			관련된 폴리곤
그룹.	콕서터군		콕서터 다이어그램		주문	서브그룹	콕서터	주문
D1.	A1.	[ ]			2	C1.	[+ ]	1	디곤
D2.	A12.	[2]			4	C2.	[2]+	2	직사각형
D3.	A2.	[3]			6	C3.	[3]+	3	정삼각형
D4.	BC2	[4]			8	C4.	[4]+	4	광장
D5.	H2	[5]			10	C5.	[5]+	5	정오각형
D6.	G2	[6]			12	C6.	[6]+	6	정육각형
Dn.	I2(n)	[n]			2n	Cn.	[n]+	n	정다각형
D2×2	A12×2	[[2]] = [4]		=	8
D3×2	A2×2	[[3]] = [6]		=	12
D4×2	BC2×2	[[4]] = [8]		=	16
D5×2	H2×2	[[5]] = [10]		=	20
D6×2	G2×2	[[6]] = [12]		=	24
Dn×2	I2(n)×2	[[n] = [2n]		=	4n

3차원

3차원의 점군, 분자의 대칭을 연구하는 데 널리 사용되었기 때문에 분자 점군이라고도 합니다.

축 또는 프리즘 그룹의 7개의 무한 패밀리와 7개의 다면체 또는 플라톤 그룹이 있습니다.쇤플라이 표기법에서는

• 축방향 그룹: C_n, S_2n, C_nh, C_nv, D_n, D_nd, D_nh
• 다면체군: T, T_dh, O, O_h, I, I_h

이러한 그룹에 결정학적 제한 정리를 적용하면 32개의 결정학적 점 그룹이 생성됩니다.

반사 그룹의 짝수/홀수 색상의 기본 도메인

C1v. 주문 2	C2v. 주문 4	C3v. 주문 6	C4v. 오더 8	C5v. 주문 10	C6v. 주문 12	...
D1h. 주문 4	D2h. 오더 8	D3h. 주문 12	D4h. 주문 16	D5h. 주문 20	D6h. 주문 24	...
Td. 주문 24	오h 오더48	나h 주문 120

국제* 지리 [2] 오르비폴드 쇤파리 콕서터 주문 1 1 1 C1. [ ]+ 1 1 22 ×1 Ci = S2 [2+,2+] 2 2 = m 1 *1 Cs = C1v = C1h [ ] 2 2 3 4 5 6 n 2 3 4 5 6 n 22 33 44 55 66 하지 않다 C2. C3. C4. C5. C6. Cn. [2]+ [3]+ [4]+ [5]+ [6]+ [n]+ 2 3 4 5 6 n mm2 3m 4mm 5m 6mm nmm nm 2 3 4 5 6 n *22 *33 *44 *55 *66 *nn C2v. C3v. C4v. C5v. C6v. Cnv. [2] [3] [4] [5] [6] [n] 4 6 8 10 12 2n 2/m 6 4/m 10 6/m 없음 2n 2 2 3 2 4 2 5 2 6 2 n 2 2* 3* 4* 5* 6* n* C2h. C3h. C4h. C5h. C6h. Cnh. [2,2+] [2,3+] [2,4+] [2,5+] [2,6+] [2,n+] 4 6 8 10 12 2n 4 3 8 5 12 2n n 4 2 6 2 8 2 10 2 12 2 2n 2 2× 3× 4× 5× 6× n× S4. S6. S8. S10. S12. S2n. [2+,4+] [2+,6+] [2+,8+] [2+,10+] [2+,12+] [2+,2n+] 4 6 8 10 12 2n

국제 지리 오르비폴드 쇤파리 콕서터 주문 222 32 422 52 622 n22 n2 2 2 3 2 4 2 5 2 6 2 n 2 222 223 224 225 226 22n D2. D3. D4. D5. D6. Dn. [2,2]+ [2,3]+ [2,4]+ [2,5]+ [2,6]+ [2,n]+ 4 6 8 10 12 2n 음. 6m2 4월 4일 10m2 6월 6일 없음 2 nm2 2 2 3 2 4 2 5 2 6 2 n 2 *222 *223 *224 *225 *226 *22n D2h. D3h. D4h. D5h. D6h. Dnh. [2,2] [2,3] [2,4] [2,5] [2,6] [2,n] 8 12 16 20 24 4n 42m 3m 82m 5m 122m 2n2m nm 4 2 6 2 8 2 10 2 12 2 n 2 2*2 2*3 2*4 2*5 2*6 2*n D2d. D3d. D4d. D5d. D6d. Dnd. [2+,4] [2+,6] [2+,8] [2+,10] [2+,12] [2+,2n] 8 12 16 20 24 4n 23 3 3 332 T [3,3]+ 12 m3 4 3 3*2 Th. [3+,4] 24 43m 3 3 *332 Td. [3,3] 24 432 4 3 432 O [3,4]+ 24 m3m 4 3 *432 오h [3,4] 48 532 5 3 532 I [3,5]+ 60 53m 5 3 *532 나h [3,5] 120

(*) Intl 엔트리가 중복되는 경우 첫 번째 엔트리는 짝수n, 두 번째 엔트리는 홀수n입니다

반사 그룹

1 - 3 거울 평면으로 정의되는 반사점 그룹은 또한 콕서터 그룹과 관련 다면체로 제공될 수 있다.[3,3] 그룹은 [3,3]로 쓰여져 첫 번째와 마지막 거울을 서로 매핑하여 대칭을 48로 두 배로 하고 [4,3] 그룹과 동형화할 수 있다.

쇤파리	콕서터군		콕서터 다이어그램			주문	관련 정기 및 프리즘 다면체
Td.	A3.	[3,3]				24	사면체
Td×Dih1 = Oh	A3×2 = BC3	[[3,3]] = [4,3]			=	48	스텔레이트 팔면체
오h	BC3	[4,3]				48	정육면체, 팔면체
나h	H3	[5,3]				120	20면체, 12면체
D3h.	A2×A1	[3,2]				12	삼각 프리즘
D3h×Dih1 = D6h	A2×A1×2	[[3],2]			=	24	육각 프리즘
D4h.	BC2×A1	[4,2]				16	사각 프리즘
D4h×Dih1 = D8h	BC2×A1×2	[[4],2] = [8,2]			=	32	팔각 프리즘
D5h.	H2×A1	[5,2]				20	오각 프리즘
D6h.	G2×A1	[6,2]				24	육각 프리즘
Dnh.	I2(n)×A1	[n,2]				4n	n-고날 프리즘
Dnh×Dih1 = D2nh	I2(n)×A1×2	[n], 2]			=	8n
D2h.	A13.	[2,2]				8	입방체
D2h×Dih1	A13×2	[[2],2] = [4,2]			=	16
D2h×Dih3 = Oh	A13×6	[3[2,2]] = [4,3]			=	48
C3v.	A2.	[1,3]				6	호소면체
C4v.	BC2	[1,4]				8
C5v.	H2	[1,5]				10
C6v.	G2	[1,6]				12
Cnv.	I2(n)	[1,n]				2n
Cnv×Dih1 = C2nv	I2(n)×2	[1, [n] = [1,2n]			=	4n
C2V	A12	[1,2]				4
C2v×Dih1	A12×2	[1,[2]]			=	8
Cs	A1	[1,1]				2

4차원

4차원 점 그룹(아키랄과 키랄)은 Conway와 Smith,^[1] 섹션 4, 표 4.1-4.3에 나열되어 있습니다.

다음 목록은 4차원 반사 그룹(하위 공간을 고정하여 저차원 반사 그룹 제외)을 제공합니다.각 그룹은 콕서터 군으로 지정되며, 3D의 다면체 군과 마찬가지로 관련된 볼록 정4-폴리토프에 의해 명명될 수 있다.관련된 순수 회전군은 각각 절반의 차수를 가지며, 예를 들어 [3,3,3]⁺은 3개의 3중 회전점과 대칭 순서 60을 갖는 '+' 지수를 갖는 괄호 콕서터 표기법으로 나타낼 수 있다.[3,3,3] 및 [3,4,3]과 같은 전후 대칭 그룹은 예를 들어 콕서터 표기법에서 이중 괄호로 표시되며, 그 순서는 240으로 2배 증가할 수 있다.

콕서터 그룹/주석		콕서터 다이어그램		주문	관련 폴리토프
A4.	[3,3,3]			120	5셀
A4×2	[[3,3,3]]			240	5셀 듀얼 컴파운드
BC4	[4,3,3]			384	16 셀/테스트
D4.	[31,1,1]			192	반신반의
D4×2 = BC4	<[3,31,1]> = [4,3,3]		=	384
D4×6 = F4	[31,1,1] = [3,4,3]		=	1152
에프4	[3,4,3]			1152	24 셀
F4×2	[[3,4,3]]			2304	24셀 이중 화합물
H4	[5,3,3]			14400	120 셀/600 셀
A3×A1	[3,3,2]			48	사면체 프리즘
A3×A1×2	[[3,3],2] = [4,3,2]		=	96	팔면체 프리즘
BC3×A1	[4,3,2]			96
H3×A1	[5,3,2]			240	이십면체 프리즘
A2×A2	[3,2,3]			36	듀오프리즘
A2×BC2	[3,2,4]			48
A2×H2	[3,2,5]			60
A2×G2	[3,2,6]			72
BC2×BC2	[4,2,4]			64
BC22×2	[[4,2,4]]			128
BC2×H2	[4,2,5]			80
BC2×G2	[4,2,6]			96
H2×H2	[5,2,5]			100
H2×G2	[5,2,6]			120
G2×G2	[6,2,6]			144
I2(p)×I2(q)	[p,2,q]			4pq
I2(2p)×I2(q)	[[p],2,q] = [2p,2,q]		=	8pq
I2(2p)×I2(2q)	[[p] ,2,[q] = [2p,2,2q]		=	16pq
I2(p)2×2	[p,2,p]			8p2
I2(2p)2×2	[[[p],2,[p]]] = [[2p,2,2p]		=	32p2
A2×A1×A1	[3,2,2]			24
BC2×A1×A1	[4,2,2]			32
H2×A1×A1	[5,2,2]			40
G2×A1×A1	[6,2,2]			48
I2(p)×A1×A1	[p, 2, 2]			8p
I2(2p)×A1×A1×2	[[p],2,2] = [2p,2,2]		=	16p
I2(p)×A12×2	[p,2,[2] = [p,2,4]		=	16p
I2(2p)×A12×4	[[p] ,2,[2] = [2p,2,4]		=	32p
A1×A1×A1×A1	[2,2,2]			16	4정통기
A12×A1×A1×2	[[2],2,2] = [4,2,2]		=	32
A12×A12×4	[[2]],2,[[2]] = [4,2,4]		=	64
A13×A1×6	[3[2,2],2] = [4,3,2]		=	96
A14×24	[3,3[2,2,2]] = [4,3,3]		=	384

5차원

다음 표는 5차원 반사 그룹(저차원 반사 그룹 제외)을 콕서터 그룹으로 나열하여 제공한다.관련된 카이랄 그룹은 각각 절반의 차수를 가지며, 예를 들어 [3,3,3,3]⁺은 4개의 3중 회전점과 대칭 순서 360을 가지며, '+' 지수를 갖는 괄호 콕서터 표기로 나타낼 수 있다.

콕서터 그룹/주석		콕서터 도표		주문	관련 정기 및 프리즘 폴리토프
A5.	[3,3,3,3]			720	51200x
A5×2	[[3,3,3,3]]			1440	5126x 듀얼 화합물
BC5	[4,3,3,3]			3840	5 큐브, 5 오르토플렉스
D5.	[32,1,1]			1920	5 데미큐브
D5×2	<[3,3,31,1]>		=	3840
A4×A1	[3,3,3,2]			240	5셀 프리즘
A4×A1×2	[[3,3,3],2]			480
BC4×A1	[4,3,3,2]			768	정사각 프리즘
F4×A1	[3,4,3,2]			2304	24 셀 프리즘
F4×A1×2	[[3,4,3],2]			4608
H4×A1	[5,3,3,2]			28800	600셀 또는 120셀 프리즘
D4×A1	[31,1,1,2]			384	데모테서랙트 프리즘
A3×A2	[3,3,2,3]			144	듀오프리즘
A3×A2×2	[[3,3],2,3]			288
A3×BC2	[3,3,2,4]			192
A3×H2	[3,3,2,5]			240
A3×G2	[3,3,2,6]			288
A3×I2(p)	[3,3,2,p]			48p
BC3×A2	[4,3,2,3]			288
BC3×BC2	[4,3,2,4]			384
BC3×H2	[4,3,2,5]			480
BC3×G2	[4,3,2,6]			576
BC3×I2(p)	[4,3,2,p]			96p
H3×A2	[5,3,2,3]			720
H3×BC2	[5,3,2,4]			960
H3×H2	[5,3,2,5]			1200
H3×G2	[5,3,2,6]			1440
H3×I2(p)	[5,3,2,p]			240p
A3×A12	[3,3,2,2]			96
BC3×A12	[4,3,2,2]			192
H3×A12	[5,3,2,2]			480
A22×A1	[3,2,3,2]			72	이중 프리즘
A2×BC2×A1	[3,2,4,2]			96
A2×H2×A1	[3,2,5,2]			120
A2×G2×A1	[3,2,6,2]			144
BC22×A1	[4,2,4,2]			128
BC2×H2×A1	[4,2,5,2]			160
BC2×G2×A1	[4,2,6,2]			192
H22×A1	[5,2,5,2]			200
H2×G2×A1	[5,2,6,2]			240
G22×A1	[6,2,6,2]			288
I2(p)×I2(q)×A1.	[p,2,q,2]			8pq
A2×A13	[3,2,2,2]			48
BC2×A13	[4,2,2,2]			64
H2×A13	[5,2,2,2]			80
G2×A13	[6,2,2,2]			96
I2(p)×A13	[p, 2, 2]			16p
A15.	[2,2,2,2]			32	5직교배
A15×(2)!	[[2],2,2,2]		=	64
A15×(2!×2!	[[2]],2,[2],2]		=	128
A15×(3!)	[3[2,2],2,2]		=	192
A15×(3!×2!)	[3[2,2],2,[[2]]		=	384
A15×(4)!	[3,3[2,2,2],2]]		=	768
A15×(5!)	[3,3,3[2,2,2,2]]		=	3840

6차원

다음 표는 6차원 반사 그룹(저차원 반사 그룹 제외)을 콕서터 그룹으로 나열하여 제공한다.관련된 순수 회전군은 각각 절반의 차수를 가지며, 예를 들어 [3,3,3,3,3]⁺은 5개의 3중 회전점과 대칭 순서 2520을 갖는 '+' 지수의 괄호 콕서터 표기로 나타낼 수 있다.

콕서터군		콕서터 도표	주문	관련 정기 및 프리즘 폴리토프
A6.	[3,3,3,3,3]		5040 (7!)	61200x
A6×2	[[3,3,3,3,3]]		10080 (2×7!)	6126x 듀얼 화합물
BC6	[4,3,3,3,3]		46080 (26×6!)	6 큐브, 6 오르토플렉스
D6.	[3,3,3,31,1]		23040 (25×6!)	6-데미큐브
E6.	[3,32,2]		51840 (72×6!)	122, 221
A5×A1	[3,3,3,3,2]		1440 (2×6!)	512x 프리즘
BC5×A1	[4,3,3,3,2]		7680 (26×5!)	5큐브 프리즘
D5×A1	[3,3,21,1]		3840 (25×5!)	5데미큐브 프리즘
A4×I2(p)	[3,3,2,p]		240p	듀오프리즘
BC4×I2(p)	[4,3,2,p]		768p
F4×I2(p)	[3,4,3,2,p]		2304p
H4×I2(p)	[5,3,2,p]		28800p
D4×I2(p)	[3,31,1,2,p]		384p
A4×A12	[3,3,3,2,2]		480
BC4×A12	[4,3,3,2,2]		1536
F4×A12	[3,4,3,2,2]		4608
H4×A12	[5,3,3,2,2]		57600
D4×A12	[3,31,1,2,2]		768
A32.	[3,3,2,3,3]		576
A3×BC3	[3,3,2,4,3]		1152
A3×H3	[3,3,2,5,3]		2880
BC32	[4,3,2,4,3]		2304
BC3×H3	[4,3,2,5,3]		5760
H32	[5,3,2,5,3]		14400
A3×I2(p)×A1	[3,3,2,p,2]		96p	듀오프리즘 프리즘
BC3×I2(p)×A1.	[4,3,2,p,2]		192p
H3×I2(p)×A1	[5,3,2,p,2]		480p
A3×A13	[3,3,2,2,2]		192
BC3×A13	[4,3,2,2,2]		384
H3×A13	[5,3,2,2,2]		960
I2(p)×I2(q)×I2(r)	[p,2,q,2,r]		8장	트라이아프리즘
I2(p)×I2(q)×A12.	[p,2,q,2,2]		16pq
I2(p)×A14	[p, 2, 2, 2, 2]		32p
A16.	[2,2,2,2,2]		64	6직교판

7차원

다음 표는 7차원 반사 그룹(저차원 반사 그룹 제외)을 콕서터 그룹으로 나열하여 제공한다.짝수 반사수로 정의되는 반차수를 갖는 각각의 관련 카이랄 그룹은 존재하며, 예를 들어 [3,3,3,3,3,3]⁺은 6개의 3중 회전점과 대칭 순서 20160을 갖는 '+' 지수의 괄호 콕서터 표기로 나타낼 수 있다.

Coxeter group		Coxeter diagram	Order	Related polytopes
A7	[3,3,3,3,3,3]		40320 (8!)	7-simplex
A7×2	[[3,3,3,3,3,3]]		80640 (2×8!)	7-simplex dual compound
BC7	[4,3,3,3,3,3]		645120 (27×7!)	7-cube, 7-orthoplex
D7	[3,3,3,3,31,1]		322560 (26×7!)	7-demicube
E7	[3,3,3,32,1]		2903040 (8×9!)	321, 231, 132
A6×A1	[3,3,3,3,3,2]		10080 (2×7!)
BC6×A1	[4,3,3,3,3,2]		92160 (27×6!)
D6×A1	[3,3,3,31,1,2]		46080 (26×6!)
E6×A1	[3,3,32,1,2]		103680 (144×6!)
A5×I2(p)	[3,3,3,3,2,p]		1440p
BC5×I2(p)	[4,3,3,3,2,p]		7680p
D5×I2(p)	[3,3,31,1,2,p]		3840p
A5×A12	[3,3,3,3,2,2]		2880
BC5×A12	[4,3,3,3,2,2]		15360
D5×A12	[3,3,31,1,2,2]		7680
A4×A3	[3,3,3,2,3,3]		2880
A4×BC3	[3,3,3,2,4,3]		5760
A4×H3	[3,3,3,2,5,3]		14400
BC4×A3	[4,3,3,2,3,3]		9216
BC4×BC3	[4,3,3,2,4,3]		18432
BC4×H3	[4,3,3,2,5,3]		46080
H4×A3	[5,3,3,2,3,3]		345600
H4×BC3	[5,3,3,2,4,3]		691200
H4×H3	[5,3,3,2,5,3]		1728000
F4×A3	[3,4,3,2,3,3]		27648
F4×BC3	[3,4,3,2,4,3]		55296
F4×H3	[3,4,3,2,5,3]		138240
D4×A3	[31,1,1,2,3,3]		4608
D4×BC3	[3,31,1,2,4,3]		9216
D4×H3	[3,31,1,2,5,3]		23040
A4×I2(p)×A1	[3,3,3,2,p,2]		480p
BC4×I2(p)×A1	[4,3,3,2,p,2]		1536p
D4×I2(p)×A1	[3,31,1,2,p,2]		768p
F4×I2(p)×A1	[3,4,3,2,p,2]		4608p
H4×I2(p)×A1	[5,3,3,2,p,2]		57600p
A4×A13	[3,3,3,2,2,2]		960
BC4×A13	[4,3,3,2,2,2]		3072
F4×A13	[3,4,3,2,2,2]		9216
H4×A13	[5,3,3,2,2,2]		115200
D4×A13	[3,31,1,2,2,2]		1536
A32×A1	[3,3,2,3,3,2]		1152
A3×BC3×A1	[3,3,2,4,3,2]		2304
A3×H3×A1	[3,3,2,5,3,2]		5760
BC32×A1	[4,3,2,4,3,2]		4608
BC3×H3×A1	[4,3,2,5,3,2]		11520
H32×A1	[5,3,2,5,3,2]		28800
A3×I2(p)×I2(q)	[3,3,2,p,2,q]		96pq
BC3×I2(p)×I2(q)	[4,3,2,p,2,q]		192pq
H3×I2(p)×I2(q)	[5,3,2,p,2,q]		480pq
A3×I2(p)×A12	[3,3,2,p,2,2]		192p
BC3×I2(p)×A12	[4,3,2,p,2,2]		384p
H3×I2(p)×A12	[5,3,2,p,2,2]		960p
A3×A14	[3,3,2,2,2,2]		384
BC3×A14	[4,3,2,2,2,2]		768
H3×A14	[5,3,2,2,2,2]		1920
I2(p)×I2(q)×I2(r)×A1	[p,2,q,2,r,2]		16pqr
I2(p)×I2(q)×A13	[p,2,q,2,2,2]		32pq
I2(p)×A15	[p,2,2,2,2,2]		64p
A17	[2,2,2,2,2,2]		128

Eight dimensions

The following table gives the eight-dimensional reflection groups (excluding those that are lower-dimensional reflection groups), by listing them as Coxeter groups. Related chiral groups exist for each with half the order, defined by an even number of reflections, and can be represented by the bracket Coxeter notation with a '+' exponent, for example [3,3,3,3,3,3,3]⁺ has seven 3-fold gyration points and symmetry order 181440.

Coxeter group		Coxeter diagram	Order	Related polytopes
A8	[3,3,3,3,3,3,3]		362880 (9!)	8-simplex
A8×2	[[3,3,3,3,3,3,3]]		725760 (2×9!)	8-simplex dual compound
BC8	[4,3,3,3,3,3,3]		10321920 (288!)	8-cube,8-orthoplex
D8	[3,3,3,3,3,31,1]		5160960 (278!)	8-demicube
E8	[3,3,3,3,32,1]		696729600 (192×10!)	421, 241, 142
A7×A1	[3,3,3,3,3,3,2]		80640	7-simplex prism
BC7×A1	[4,3,3,3,3,3,2]		645120	7-cube prism
D7×A1	[3,3,3,3,31,1,2]		322560	7-demicube prism
E7×A1	[3,3,3,32,1,2]		5806080	321 prism, 231 prism, 142 prism
A6×I2(p)	[3,3,3,3,3,2,p]		10080p	duoprism
BC6×I2(p)	[4,3,3,3,3,2,p]		92160p
D6×I2(p)	[3,3,3,31,1,2,p]		46080p
E6×I2(p)	[3,3,32,1,2,p]		103680p
A6×A12	[3,3,3,3,3,2,2]		20160
BC6×A12	[4,3,3,3,3,2,2]		184320
D6×A12	[33,1,1,2,2]		92160
E6×A12	[3,3,32,1,2,2]		207360
A5×A3	[3,3,3,3,2,3,3]		17280
BC5×A3	[4,3,3,3,2,3,3]		92160
D5×A3	[32,1,1,2,3,3]		46080
A5×BC3	[3,3,3,3,2,4,3]		34560
BC5×BC3	[4,3,3,3,2,4,3]		184320
D5×BC3	[32,1,1,2,4,3]		92160
A5×H3	[3,3,3,3,2,5,3]
BC5×H3	[4,3,3,3,2,5,3]
D5×H3	[32,1,1,2,5,3]
A5×I2(p)×A1	[3,3,3,3,2,p,2]
BC5×I2(p)×A1	[4,3,3,3,2,p,2]
D5×I2(p)×A1	[32,1,1,2,p,2]
A5×A13	[3,3,3,3,2,2,2]
BC5×A13	[4,3,3,3,2,2,2]
D5×A13	[32,1,1,2,2,2]
A4×A4	[3,3,3,2,3,3,3]
BC4×A4	[4,3,3,2,3,3,3]
D4×A4	[31,1,1,2,3,3,3]
F4×A4	[3,4,3,2,3,3,3]
H4×A4	[5,3,3,2,3,3,3]
BC4×BC4	[4,3,3,2,4,3,3]
D4×BC4	[31,1,1,2,4,3,3]
F4×BC4	[3,4,3,2,4,3,3]
H4×BC4	[5,3,3,2,4,3,3]
D4×D4	[31,1,1,2,31,1,1]
F4×D4	[3,4,3,2,31,1,1]
H4×D4	[5,3,3,2,31,1,1]
F4×F4	[3,4,3,2,3,4,3]
H4×F4	[5,3,3,2,3,4,3]
H4×H4	[5,3,3,2,5,3,3]
A4×A3×A1	[3,3,3,2,3,3,2]			duoprism prisms
A4×BC3×A1	[3,3,3,2,4,3,2]
A4×H3×A1	[3,3,3,2,5,3,2]
BC4×A3×A1	[4,3,3,2,3,3,2]
BC4×BC3×A1	[4,3,3,2,4,3,2]
BC4×H3×A1	[4,3,3,2,5,3,2]
H4×A3×A1	[5,3,3,2,3,3,2]
H4×BC3×A1	[5,3,3,2,4,3,2]
H4×H3×A1	[5,3,3,2,5,3,2]
F4×A3×A1	[3,4,3,2,3,3,2]
F4×BC3×A1	[3,4,3,2,4,3,2]
F4×H3×A1	[3,4,2,3,5,3,2]
D4×A3×A1	[31,1,1,2,3,3,2]
D4×BC3×A1	[31,1,1,2,4,3,2]
D4×H3×A1	[31,1,1,2,5,3,2]
A4×I2(p)×I2(q)	[3,3,3,2,p,2,q]			triaprism
BC4×I2(p)×I2(q)	[4,3,3,2,p,2,q]
F4×I2(p)×I2(q)	[3,4,3,2,p,2,q]
H4×I2(p)×I2(q)	[5,3,3,2,p,2,q]
D4×I2(p)×I2(q)	[31,1,1,2,p,2,q]
A4×I2(p)×A12	[3,3,3,2,p,2,2]
BC4×I2(p)×A12	[4,3,3,2,p,2,2]
F4×I2(p)×A12	[3,4,3,2,p,2,2]
H4×I2(p)×A12	[5,3,3,2,p,2,2]
D4×I2(p)×A12	[31,1,1,2,p,2,2]
A4×A14	[3,3,3,2,2,2,2]
BC4×A14	[4,3,3,2,2,2,2]
F4×A14	[3,4,3,2,2,2,2]
H4×A14	[5,3,3,2,2,2,2]
D4×A14	[31,1,1,2,2,2,2]
A3×A3×I2(p)	[3,3,2,3,3,2,p]
BC3×A3×I2(p)	[4,3,2,3,3,2,p]
H3×A3×I2(p)	[5,3,2,3,3,2,p]
BC3×BC3×I2(p)	[4,3,2,4,3,2,p]
H3×BC3×I2(p)	[5,3,2,4,3,2,p]
H3×H3×I2(p)	[5,3,2,5,3,2,p]
A3×A3×A12	[3,3,2,3,3,2,2]
BC3×A3×A12	[4,3,2,3,3,2,2]
H3×A3×A12	[5,3,2,3,3,2,2]
BC3×BC3×A12	[4,3,2,4,3,2,2]
H3×BC3×A12	[5,3,2,4,3,2,2]
H3×H3×A12	[5,3,2,5,3,2,2]
A3×I2(p)×I2(q)×A1	[3,3,2,p,2,q,2]
BC3×I2(p)×I2(q)×A1	[4,3,2,p,2,q,2]
H3×I2(p)×I2(q)×A1	[5,3,2,p,2,q,2]
A3×I2(p)×A13	[3,3,2,p,2,2,2]
BC3×I2(p)×A13	[4,3,2,p,2,2,2]
H3×I2(p)×A13	[5,3,2,p,2,2,2]
A3×A15	[3,3,2,2,2,2,2]
BC3×A15	[4,3,2,2,2,2,2]
H3×A15	[5,3,2,2,2,2,2]
I2(p)×I2(q)×I2(r)×I2(s)	[p,2,q,2,r,2,s]		16pqrs
I2(p)×I2(q)×I2(r)×A12	[p,2,q,2,r,2,2]		32pqr
I2(p)×I2(q)×A14	[p,2,q,2,2,2,2]		64pq
I2(p)×A16	[p,2,2,2,2,2,2]		128p
A18	[2,2,2,2,2,2,2]		256

See also

• Point groups in two dimensions
• Point groups in three dimensions
• Point groups in four dimensions
• Crystallography
• Crystallographic point group
• Molecular symmetry
• Space group
• X-ray diffraction
• Bravais lattice
• Infrared spectroscopy of metal carbonyls

References

Further reading

• H. S. M. Coxeter: Kaleidoscopes: Selected Writings of H. S. M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN978-0-471-01003-6[2]
  • (Paper 23) H. S. M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559–591]
• H. S. M. Coxeter and W. O. J. Moser. Generators and Relations for Discrete Groups 4th ed, Springer-Verlag. New York. 1980
• N. W. Johnson: Geometries and Transformations, (2018) Chapter 11: Finite symmetry groups

External links

• Web-based point group tutorial (needs Java and Flash)
• Subgroup enumeration (needs Java)
• The Geometry Center: 2.1 Formulas for Symmetries in Cartesian Coordinates (two dimensions)
• The Geometry Center: 10.1 Formulas for Symmetries in Cartesian Coordinates (three dimensions)