5와섹스

5와섹스 헥사테론(hix)
유형	균일 5인치대
슐레플리 기호	{3⁴}
콕시터 다이어그램
4시 15분	6	6 {3,3,3}
세포	15	15 {3,3}
얼굴	20	20 {3}
가장자리	15
정점	6
정점수	5세포
콕시터군	A₅, [3⁴], 주문 720
이중	자화자기의
기준점	(0,0,0,0,0,1)
할레라디우스	0.645497
특성.	볼록, 이등변 정규, 자기 보정

5차원 지오메트리에서 5단원형은 자기 이중 정규5 폴리토프다.정점 6개, 가장자리 15개, 삼각면 20개, 사면체 15개, 5세포 6개가 있다.cos⁻¹(cos)의 2면각이다.1/5) 또는 약 78.46°

5-심플렉스(Simplex)는 이 문제에 대한 해결책이다.15개의 성냥개비를 이용하여 20개의 정삼각형을 만들어라. 여기서 모든 삼각형의 각 면은 정확히 하나의 성냥개비가 된다.

대체 이름

5차원에서는 6면체 폴리토프로서 헥사테론 또는 헥사-5토페라고도 할 수 있다.헥사테론이라는 이름은 6개의 면을 가진다는 이유로 육각형을, 4차원 면을 가진다는 이유로 테론을 사용한 것에서 유래되었다.

조나단 보우어스에 의해, 육각체에는 약자 hix가 주어진다.^[1]

구성으로

이 구성 매트릭스는 5-단순함을 나타낸다.행과 열은 꼭지점, 가장자리, 면, 셀 및 4-페이스를 나타낸다.대각선 숫자는 전체 5-단순에서 각 원소 중 얼마나 많은 원소가 발생하는지를 나타낸다.비대각 숫자는 열의 요소 중 몇 개가 행의 요소 안에서 또는 열 요소에서 발생하는지 알려준다.이 자가이중 심플렉스 매트릭스는 180도 회전과 동일하다.^[2]^[3]

${\bmatrix}{\display}6&10&10&5\\\2&15&4&4\\3&3&20&3\\4&4&4&15&2\5&10&5&6\end{bmatrix}}}}$

정규 육각 좌표

육각형은 5-셀의 다른 모든 정점으로부터 등거리인 6번째 정점을 추가함으로써 5-셀로부터 구성될 수 있다.

에지 길이가 2인 원점 중심 정규 육각체의 정점에 대한 데카르트 좌표는 다음과 같다.

{\sqrt}&\reft}{1}{\sqrt{15}},\\tfrac {1}{\tfrac {1}{\sqrt{6}}},\\\tfrac {1}{\sqrt{3},\pm 1\rig)\\[5pt]&\left\tfrac {1}{\sqrt {15}},\\\\tfrac {1}{\sqrt {10}},\\\\tfrac {1}{\sqrt {6}},\\\tfrac {2}{3}},\0\오른쪽)\\[5pt]&\left\tfrac {1}{\sqrt {15}},\\\\tfrac {1}{\sqrt {10}},\\\\tfrac {3}{\sqrt {2},\ 0\\오른쪽)\\[5pt]&\left\tfrac {1}{\sqrt {15}},\-{\\tfrac {2{\\sqrt {2}}:{\sqrt {5},\ 0,\\오른쪽)\\[5pt]&\왼쪽{\tfrac {5}{\sqrt{5}}{\sqrt{3}}\0,\0,\0,\0\오른쪽)\end{aigned}}}

5-심플렉스 정점은 (0,0,0,0,0,0,1) 또는 (0,1,1,1,1)의 순열로서 6-공간에서 하이퍼플레인 위에 보다 간단하게 위치할 수 있다.이러한 구조는 각각 6관이나 6관의 면으로 볼 수 있다.

투사된 이미지

맞춤법 투사
A을_k 콕시터 평면	A을₅	A을₄
그래프
치측 대칭	[6]	[5]
A을_k 콕시터 평면	A을₃	A을₂
그래프
치측 대칭	[4]	[3]

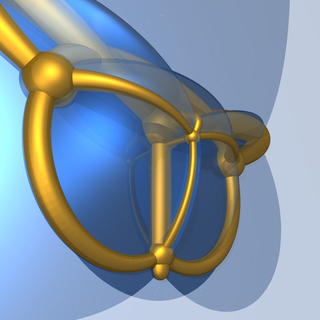슐레겔 도표 5D에서 헥사터론 4D에서 3D로 입체 투영.

하부 대칭 형태

하위 대칭 형태는 [3,3] 대칭 순서 120을 갖는 5-셀 피라미드( )v{3,3,3}, 4-공간 하이퍼플레인에서 5-셀 베이스로 구성되고, 하이퍼플레인 위의 꼭지점으로 구성된다.피라미드의 5개 면은 5세포 세포로 이루어져 있다.이것들은 잘린 6-관처럼 잘린 정규 6-폴리탑의 꼭지점으로 보인다.

또 다른 형태는 { }v{3,3}이며, 대칭 순서 48, 직교 디곤과 직교 오프셋 4면체의 결합이며, 모든 정점 쌍이 서로 연결되어 있다.또 다른 형태는 {3}v{3}, 대칭 순서 [3,3] 대칭 순서 36, 확장 대칭 [3,2,3], 순서 72이다.이것은 두 개의 직교 삼각형, 직교 오프셋의 결합을 나타내며, 정점 쌍이 서로 연결되어 있다.

이것들은 6-큐브와 6-단순 삼중수소처럼, 비트롤링된 정규 6-폴리탑의 꼭지점에서 볼 수 있다.여기서 가장자리 라벨은 해당 방향을 따라 면의 유형을 나타내며, 따라서 다른 가장자리 길이를 나타낸다.

잘린 6-단순에 대한 정점 그림

( )v{3,3,3}		{ }v{3,3}		{3}v{3}

잘린 6입방근	잘린 6인치	6-145cmx의 비트코인	6인치 짜리 비트코인	삼중수소 함유량이 6-145배인

화합물

이중 구성에서 두 개의 5단계의 혼합물은 A6 Coxeter 평면 투영에서 볼 수 있으며, 빨간색과 파란색 5단계의 정점과 가장자리가 있다.이 화합물은 대칭이 [3,3,3,3]이며, 순서는 1440이다.이 두 5단계의 교차점은 균일한 양방향 5단추다. = ∩ .

관련 균일 5폴리톱

콕시터가 1시리즈로_3k 표현한 균일한 폴리토페스와 허니콤의 치수계열에서 최초다.퇴보한 4차원 사례는 사면 호소헤드론인 3-sphere 타일링으로 존재한다.

1차원_3k 도형

공간	유한한				유클리드 주	쌍곡선
n	4	5	6	7	8	9
콕시터 무리를 짓다	A₃A₁	A을₅	D₆	E₇	${\tilde {E}}_{7}$ ~ ${\tilde {E}}_{7}$ ${\$ =E₇⁺	${\bar {T}}_{8}$ 8 ${\$ ${\bar {T}}_{8}$ E₇⁺⁺
콕시터 도표를 만들다
대칭	[3^−1,3,1]	[3^0,3,1]	[3^1,3,1]	[3^2,3,1]	[[3^3,3,1]]	[3^4,3,1]
주문	48	720	23,040	2,903,040	∞
그래프					-	-
이름	1_3,-1	1₃₀	1₃₁	1₃₂	1₃₃	1₃₄

콕시터가 3시리즈로_k1 표현한 균일한 폴리토페스와 허니콤의 치수계열에서 최초다.퇴보한 4차원 케이스는 3-sphere 타일링, 4면 다이드론으로서 존재한다.

3차원_k1 그림

공간	유한한				유클리드 주	쌍곡선
n	4	5	6	7	8	9
콕시터 무리를 짓다	A₃A₁	A을₅	D₆	E₇	${\tilde {E}}_{7}$ ~ ${\tilde {E}}_{7}$ ${\$ =E₇⁺	${\bar {T}}_{8}$ 8 ${\$ ${\bar {T}}_{8}$ E₇⁺⁺
콕시터 도표를 만들다
대칭	[3^−1,3,1]	[3^0,3,1]	[[3^1,3,1]] = [4,3,3,3,3]	[3^2,3,1]	[3^3,3,1]	[3^4,3,1]
주문	48	720	46,080	2,903,040	∞
그래프					-	-
이름	3_1,-1	3₁₀	3₁₁	3₂₁	3₃₁	3₄₁

5-단순은 2개의₂₀ 폴리토프처럼 2차원의 시리즈 2에서_2k 첫 번째다.

n차원의 2개_2k 그림

공간	유한한			유클리드 주	쌍곡선
n	4	5	6	7	8
콕시터 무리를 짓다	A₂A₂	A을₅	E₆	${\tilde {E}}_{6}$ ~ ${\tilde {E}}_{6}$ ${\$ =E₆⁺	E₆⁺⁺
콕시터 도표를 만들다
그래프				∞	∞
이름	2_2,-1	2₂₀	2₂₁	2₂₂	2₂₃

정규 5-심플렉스(Simplex)는 [3,3,3,3] Coxeter 그룹에 기초한 19개의 균일한 폴리테라 중 하나이며, 모두 여기₅ A Coxeter 평면 직교 투영에 나타나 있다.(수직은 투영 오버랩 순서, 빨간색, 주황색, 노란색, 녹색, 청록색, 청록색, 파란색, 보라색으로 색상이 지정되며 정점이 점점 더 많아짐)

A5 폴리토페스
t₀	t₁	t₂	t_0,1	t_0,2	t_1,2	t_0,3
t_1,3	t_0,4	t_0,1,2	t_0,1,3	t_0,2,3	t_1,2,3	t_0,1,4
t_0,2,4	t_0,1,2,3	t_0,1,2,4	t_0,1,3,4	t_0,1,2,3,4

메모들

^ Klitzing, Richard. "5D uniform polytopes (polytera) x3o3o3o3o — hix".
^ Coxeter 1973, §1.8 구성
^ Coxeter, H.S.M. (1991). Regular Complex Polytopes (2nd ed.). Cambridge University Press. p. 117. ISBN 9780521394901.

참조

Gosset, T. (1900). "On the Regular and Semi-Regular Figures in Space of n Dimensions". Messenger of Mathematics. Macmillan. pp. 43–.
콕시터, H.S.M.:
- — (1973). "Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)". Regular Polytopes (3rd ed.). Dover. pp. 296. ISBN 0-486-61480-8.
- Sherk, F. Arthur; McMullen, Peter; Thompson, Anthony C.; Weiss, Asia Ivic, eds. (1995). Kaleidoscopes: Selected Writings of H.S.M. Coxeter. Wiley. ISBN 978-0-471-01003-6.
  - (22쪽)
  - (23쪽)
  - (24쪽)
Conway, John H.; Burgiel, Heidi; Goodman-Strass, Chaim (2008). "26. Hemicubes: 1_n1". The Symmetries of Things. p. 409. ISBN 978-1-56881-220-5.
Johnson, Norman (1991). "Uniform Polytopes" (Manuscript). {{cite journal}}:Cite 저널은 필요로 한다. journal=(도움말)
- Johnson, N.W. (1966). The Theory of Uniform Polytopes and Honeycombs (PhD). University of Toronto.

외부 링크

Olshevsky, George. "Simplex". Glossary for Hyperspace. Archived from the original on 4 February 2007.
다양한 차원의 폴리탑, 조나단 보우어
다차원 용어집

v t 치수 2-10의 기본 볼록형 일반 및 균일한 폴리토프
가족	A_n	B_n	I₂(p) / D_n	E₆ / E₇ / E₈ / F₄ / G₂	H_n
정규 다각형	삼각형	사각형	p-곤	육각형	펜타곤
균일다면체	사면체	옥타헤드론 • 큐브	데미큐브		도데카헤드론 • 이코사헤드론
균일 폴리초론	펜타코론	16-셀 • 테세락트	데미테세락트	24셀	120 셀 • 600 셀
제복5폴리토프	5와섹스	5정형 • 5정형	5데미큐브
제복6폴리토프	6-630x	6-정통 • 6-118	6데미큐브	1₂₂ • 2₂₁
제복7폴리토프	7시 15분	7정맥 • 7정맥	7데미큐브	1₃₂ • 2₃₁ • 3₂₁
제복8폴리토프	8시 15분	8정형 • 8정형	8데미큐브	1₄₂ • 2₄₁ • 4₂₁
제복9폴리토프	9시 15분	9-정통 • 9-11	9데미큐브
균일 10폴리토프	10센트짜리	10정형 • 10정형	10데미큐브
균일 n폴리토프	n-제곱스	n-직관 • n-직관	n-데미큐브	1_k2 • 2_k1 • k₂₁	n-자갈 폴리토프
주제: 폴리토페 패밀리 • 일반 폴리토페 • 일반 폴리토페 및 화합물 목록

[1] Klitzing, Richard. "5D uniform polytopes (polytera) x3o3o3o3o — hix".

[2] Coxeter 1973, §1.8 구성

[3] Coxeter, H.S.M. (1991). Regular Complex Polytopes (2nd ed.). Cambridge University Press. p. 117. ISBN 9780521394901.

[1]

[2]

[3]

Search