일반 스큐 다면체

기하학에서 정규 스큐 폴리헤드라는 평면이 아닌 면이나 꼭지점 형상의 가능성을 포함하는 일반 폴리헤드라의 집합에 대한 일반화다. 콕세터는 새로운 4차원 일반 다면체를 만들어낸 꼬치 꼭지점 형상을 바라보았고, 훨씬 후일 브란코 그룬바움도 평범한 꼬치 얼굴을 바라보았다.^[1]

3공간 이상에 걸쳐 있는 무한정 일반 스큐 폴리헤드라를 일반 스큐 아페이로헤드라 한다.

역사

콕세터에 따르면 1926년 존 플린더스 페트리는 일반 스큐 폴리곤(비 평면 폴리곤)의 개념을 일반 스큐 폴리헤드라에 일반화했다.

Coxeter는 이러한 수치들에 대해 수정된 Schléfli 기호{ $l, m$ $n}$ 을 제공했는데, 이 기호들은 정점 수치를 암시하는 { $l, m}$ 과 정점 $주위$ 의 m l-곤과 n-곤홀을 의미한다. 그들의 꼭지점 수치는 두 평면 사이를 지그재그하는, 꼬불꼬불한 다각형이다.

${l, m$ $n}($ 으)로 표현되는 일반 스큐 폴리헤드라는 다음 방정식을 따른다.

2\cos {\frac {\pi }{l}}\cos {\frac {\pi }{n}}}

첫 번째 세트 { $l, m$ $n}$ 은(는) 5개의 볼록한 플라토닉 고형분과 1개의 비콘벡스 케플러-핀소 고형분을 반복한다.

${l, m n}$	얼굴	가장자리	정점	$p$	다면체	대칭 주문
{3,3 3} = {3,3}	4	6	4	0	사면체	12
{3,4 4} = {3,4}	8	12	6	0	팔면체	24
{4,3 4} = {4,3}	6	12	8	0	큐브	24
{3,5 5} = {3,5}	20	30	12	0	이코사헤드론	60
{5,3 5} = {5,3}	12	30	20	0	도데카헤드론	60
{5,5 3} = {5,5/2}	12	30	12	4	대두면체	60

유한정규다면체

A4 Coxeter 평면 투영

{4, 6 3}	{6, 4 3}
런케이티드 5-셀 (정점 20개, 가장자리 60개)	비트런티드 5-셀 (정점 30개, 가장자리 60개)
F4 Coxeter 평면 투영

{4, 8 3}	{8, 4 3}
런케이티드 24셀 (정점, 576 가장자리)	비트런티드 24셀 (288 꼭지점, 576 가장자리)

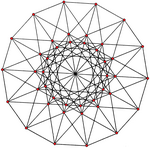{3,8 ,4} = {3,8}₈	{4,6 ,3} = {4,6}₆
꼭지점 42개, 가장자리 168개	56 꼭지점, 168 가장자리
4차원 일반 스큐 폴리헤드라의 일부는 상위 4개 투영에서와 같이 균일한 폴리초라 안에 들어맞는다.

콕시터는 또한 그의 논문 "3차원 및 4차원의 정규 스큐 폴리헤드라와 그들의 위상학적 유사점"에 유한한 일반 폴리헤드라의 더 큰 세트를 열거했다.

무한 스큐 폴리헤드라가 볼록한 균일 벌집들의 세포들 사이의 다지관 표면을 나타내는 것처럼, 유한 형태는 모두 균일한 4폴리탑의 세포들 내의 다지관 표면을 나타낸다.

{2p, 2q r} 형식의 폴리헤드라는 [(p,r,q,r)]의 Coxeter 그룹 대칭과 관련이 있으며, q가 2일 때 선형 [r,p,r]로 감소한다. Coxeter는 이러한 대칭을 자신의 추상적 그룹(2p,2q 2,r)에 이형성이 있다고 말하는 [[,r,q,r]⁺로 부여한다. 관련 벌집형에는 확장된 대칭[[p,r,q,r]^[2]이 있다.

{2p,4r}은(는) 비트런딩된 {r,p,r} 균일한 4-118tope의 {2p} 면으로 표시되고, {4,2p r}은(는) 런닝된 {r,p,r}의 사각형 면으로 표시된다.

{4,4n}은(는) n-n 듀오프리즘을 생성하며, 구체적으로 {4}x{4} 테세락트 내부에 {4,4}이(가) 적합하다.

{4,4n} 용액은 두 개의 정사각형 면을 나타내며, n-곤의 면은 구멍으로 되어 있고 벼랑 끝으로 된 토루스(torus)와 두실린더(duocylinder)의 근사치를 나타낸다.	{4,4 6}은(는) 원근 투영에서 6,6 듀오프리즘에서 추출한 정사각형으로 보이는 36개의 정사각형 면을 가지고 있다.	{4,4 4}은(는) 16개의 사각면을 가지며, 테서락트 내의 얼굴 부분 집합으로 존재한다.

60개의 삼각형으로 이루어진 고리는 600셀의 면의 부분집합 안에 규칙적인 꼬치 다면체를 만든다.

4차원의 유한 폴리헤드라
{l, m n}	얼굴	가장자리	정점	p	구조	대칭	주문	관련 균일 폴리초라
{4,4 3}	9	18	9	1	D₃xD₃	[[3,2,3]⁺]	9	3-3 듀오프리즘
{4,4 4}	16	32	16	1	D₄xD₄	[[4,2,4]⁺]	16	4-4 듀오프리즘 또는 큐브랙트
{4,4 5}	25	50	25	1	D₅xD₅	[[5,2,5]⁺]	25	5-5 듀오프리즘
{4,4 6}	36	72	36	1	D₆xD₆	[[6,2,6]⁺]	36	6-6 듀오프리즘
{4,4n}	n²	2n²	n²	1	D_nxD_n	[[n,2,n]⁺]	n²	n-n 듀오프리즘
{4,6 3}	30	60	20	6	S5	[[3,3,3]⁺]	60	런케이티드 5-셀
{6,4 3}	20	60	30	6	S5	[[3,3,3]⁺]	60	비트런티드 5-셀
{4,8 3}	288	576	144	73		[[3,4,3]⁺]	576	런케이티드 24셀
{8,4 3}	144	576	288	73		[[3,4,3]⁺]	576	비트런티드 24셀

펜타그램 용액
{l, m n}	얼굴	가장자리	정점	p	구조	대칭	주문	관련 균일 폴리초라
{4,5 5}	90	180	72	10	A6	[[5/2,5,5/2]⁺]	360	룬케이티드 그랜드 스티어 120셀
{5,4 5}	72	180	90	10	A6	[[5/2,5,5/2]⁺]	360	120셀을 감싼 그랜드 스텔링

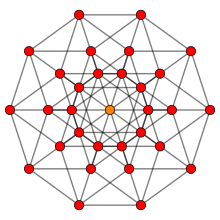
정점과 가장자리를 보여주는 B5 Coxeter 평면 투영에서 볼 수 있는 5-큐브의 32 정점과 80개의 가장자리 내에서 {4,5 4}을(를) 실현할 수 있다. 5큐브의 80제곱면은 꼬치 다면체의 40제곱면과 40제곱 구멍이 된다.

{l, m n}	얼굴	가장자리	정점	p	구조	주문	관련 균일 폴리토페스
{4,5 4}	40	80	32	5	?	160	5각 정점(±1,±1,±1,±1,±1) 및 가장자리
{5,4 4}	32	80	40	5	?	160	정류된 5정맥 정점(±1,±1,0,0,0)
{4,7 3}	42	84	24	10	LF(2,7)	168
{7,4 3}	24	84	42	10	LF(2,7)	168
{5,5 4}	72	180	72	19	A6	360
{6,7 3}	182	546	156	105	LF(2,13)	1092
{7,6 3}	156	546	182	105	LF(2,13)	1092
{7,7 3}	156	546	156	118	LF(2,13)	1092
{4,9 3}	612	1224	272	171	LF(2,17)	2448
{9,4 3}	272	1224	612	171	LF(2,17)	2448
{7,8 3}	1536	5376	1344	1249	?	10752
{8,7 3}	1344	5376	1536	1249	?	10752

최종 세트는 Coxeter의 추가 확장 형식 {q1,m q2,q3...} 또는 q2가 지정되지 않은 경우: {l, m, q}. 이것들은 또한 정규 유한 지도 또는 {l, m},_2q 그룹 G를^l,m,q 나타낼 수 있다.^[3]

{l, m, q} 또는 {l, m}_2q	얼굴	가장자리	정점	p	구조	주문	관련복합다면체
{3,6,q} = {3,6}_2q	2q²	3q²	q²	1	G^3,6,2q	2q²
{3,2q ,3} = {3,2q}₆	2q²	3q²	3q	(q-1)*(q-2)/2	G^3,6,2q	2q²
{3,7 ,4} = {3,7}₈	56	84	24	3	LF(2,7)	168
{3,8 ,4} = {3,8}₈	112	168	42	8	PGL(2,7)	336	(1 1 1₁⁴)⁴,
{4,6 ,3} = {4,6}₆	84	168	56	15	PGL(2,7)	336	(1⁴ 1⁴ 1₁)⁽³⁾,
{3,7 ,6} = {3,7}₁₂	364	546	156	14	LF(2,13)	1092
{3,7 ,7} = {3,7}₁₄	364	546	156	14	LF(2,13)	1092
{3,8 ,5} = {3,8}₁₀	720	1080	270	46	G^3,8,10	2160	(1 1 1₁⁴)⁵,
{3,10 ,4} = {3,10}₈	720	1080	216	73	G^3,8,10	2160	(1 1 1₁⁵)⁴,
{4,6 ,2} = {4,6}₄	12	24	8	3	S4×S2	48
{5,6 ,2} = {5,6}₄	24	60	20	9	A5×S2	120
{3,11 ,4} = {3,11}₈	2024	3036	552	231	LF(2,23)	6072
{3,7 ,8} = {3,7}₁₆	3584	5376	1536	129	G^3,7,17	10752
{3,9 ,5} = {3,9}₁₀	12180	18270	4060	1016	LF(2,29)×A3	36540

상위 치수

일반 스큐 폴리헤드라는 일반 폴리토피나 허니컴에 임베딩하여 4 이상의 치수로 제작할 수도 있다. 예를 들어, 정규 이코사헤드론은 6데미큐브의 꼭지점에 삽입될 수 있다; 이것은 H. S. M. Coxeter에 의해 정규 이코사헤드론이라고 명명되었다. 도데카헤드론은 비슷하게 10데미큐브에 삽입될 수 있다.^[4]

참고 항목

메모들

^ 추상 일반 폴리토페스, 페이지 7, 페이지 17
^ Coxeter, 정규 및 반정규 폴리토페 II 2.34)
^ Coxeter 및 Moser, 생성자 및 이산 그룹 관계, 8.6절 Petrie polygons를 명시한 지도
^ Deza, Michael; Shtogrin, Mikhael (1998). "Embedding the graphs of regular tilings and star-honeycombs into the graphs of hypercubes and cubic lattices". Advanced Studies in Pure Mathematics. Arrangements – Tokyo 1998: 77. doi:10.2969/aspm/02710073. ISBN 978-4-931469-77-8. Retrieved 4 April 2020.

참조

Peter McMullen, 4차원 정규 다면체, 이산 & 계산 기하학 2007년 9월, 제38권, 제2, 페이지 355–387
Coxeter, 일반 폴리토페스, 제3판, (1973) 도버판, ISBN 0-486-61480-8
케일리디스코어: F가 편집한 H. S. M. Coxeter의 선별된 글. 아서 셔크, 피터 맥멀런, 앤서니 C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (용지 2) H.S.M. Coxeter, "일반 해면체 또는 스큐 폴리헤드라", Scripta Mathematica 6 (1939) 240-244.
- (용지 22) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 I, [산술] Zeit. 46 (1940) 380–407, MR 2,10]
- (용지 23) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 II, [수학] Zeit. 188 (1985) 559–591]
콕시터, 기하학의 아름다움: 12편의 에세이, 도버 출판물, 1999년 ISBN0-486-40919-8(3장 4차원의 정규 스큐 폴리헤드라와 그 위상학적 유사점, 런던 수학 학회의 절차, 제2, 제43권, 1937년)
- Coxeter, H. S. M. 정규 스큐 3차원 및 4차원 폴리헤드라. Proc. 런던 수학. Soc. 43, 33-62, 1937.
가너, C. W. L. 쌍곡선 3공간의 일반 스큐 폴리헤드라. 캔. J. 수학. 19, 1179-1186, 1967.
E. Schulte, J.M. Wills On Coxeter의 정규 스큐 다면체, 이산수학, 60권, 6월-1986년 7월 페이지 253-262

[1] 추상 일반 폴리토페스, 페이지 7, 페이지 17

[2] Coxeter, 정규 및 반정규 폴리토페 II 2.34)

[3] Coxeter 및 Moser, 생성자 및 이산 그룹 관계, 8.6절 Petrie polygons를 명시한 지도

[4] Deza, Michael; Shtogrin, Mikhael (1998). "Embedding the graphs of regular tilings and star-honeycombs into the graphs of hypercubes and cubic lattices". Advanced Studies in Pure Mathematics. Arrangements – Tokyo 1998: 77. doi:10.2969/aspm/02710073. ISBN 978-4-931469-77-8. Retrieved 4 April 2020.

[1]

[2]

[3]

[4]

Search

일반 스큐 다면체

네임스페이스

더

목차

역사

유한정규다면체

상위 치수

참고 항목

메모들

참조