꼬치 아피로헤드론

기하학에서 꼬치 아피로헤드론은 비평면 또는 비평면 정점 형상으로 구성된 무한 스큐 다면체로서, 접지 않고 무한히 연장하여 닫힌 표면을 형성할 수 있다.

꼬치 아페이로헤드라는 다면 해면체라고도 불린다.

많은 것들이 일부 세포가 제거된 벌집의 다각형 표면인 볼록한 균일한 벌집과 직접적으로 관련되어 있다.특징적으로 무한대 꼬치 다면체는 3차원 공간을 두 반으로 나눈다.만약 1/2을 고체라고 생각한다면, 그 수치를 부분 벌집이라고 부르기도 한다.

일반꼬치아페이로헤드라

콕세터에 따르면 1926년 존 플린더스 페트리는 일반 스큐 폴리곤(비 평면 폴리곤)의 개념을 일반 스큐 폴리헤드라(아페이로헤드라)로 일반화했다.^[1]

콕시터와 페트리는 이 중 3개의 공간을 채운 3개를 발견했다.

일반꼬치아페이로헤드라
{4,6 4} 뮤큐브	{6,4 4} 뮤옥타헤드론	{6,6 3} 돌연변이체

또한 {4,6}, {6,4}, {6,6} 유형의 키랄 꼬치 아페이로헤드라도 존재한다.이 꼬치 아페이로헤드라는 정점 변환, 가장자리 변환, 얼굴 변환이지만 거울 대칭은 아니다(Schulte 2004).

유클리드 3-공간을 넘어 1967년 C. W. L. 가너는 쌍곡 3-공간에서 31개의 정규 스큐 다면체를 발표했다.^[2]

고트의 일반 가성면체

J. Richard Gott는 1967년에 더 큰 7개의 무한 스큐 다면체를 출판했는데, 이 중 콕시터의 3개는 {4,6,6,4},{6},4,5},{3,8},{3,10} 등이며, 4개의 새로운 것: {5,5}, {4,5},8},3,10}^[3][4]을 포함하여 그가 일반 유사면체라고 불렀다.

Gott는 그의 새로운 수치를 허락하기 위해 규칙성의 정의를 완화했다.Coxeter와 Petrie가 정점이 대칭이어야 한다고 요구했던 곳에서는 Gott는 정점이 일치해야 한다고 요구하였다.따라서 고트의 새로운 예는 콕시터와 페트리의 정의에 의해 규칙적이지 않다.

Gott는 정규 다면체, 정규 기울기, 정규 유사 다면체의 전체 세트를 정규 다면체라고 불렀고, {p,q} Schléfli 기호로 나타낼 수 있으며, 각 꼭지점 주위에 p-곤란 면으로 q를 표시된다.그러나 '의사체'라는 용어도 고트의 규칙성에 대한 정의도 널리 쓰이지 못했다.

결정학자 A.F. 1960년대 웰스는 또한 꼬치 아페이로헤드라 목록을 발표했다.Melinda Green은 1998년에 더 많은 것을 출판했다.

{p,q}	세포 꼭지점 부근.	꼭지점 얼굴들	더 큰 무늬를 넣다	스페이스 그룹			관련2 H 궤도의 표기법
				큐빅 스페이스 무리를 짓다	콕시터 표기법	피브리폴드 표기법
{4,5}	큐브 3개			임3m	[[4,3,4]]	8°:2	*4222
{4,5}	잘린 팔면체 1개 육각 프리즘 2개			I3	[[4,3+,4]]	8°:2	2*42
{3,7}	팔면체 1개 이코사면체 1개			Fd3	[[3[4]]]+	2°−	3222
{3,8}	정육면체 2개			Fm3m	[4,(3,4)+]	2−−	32*
{3,9}	사면체 1개 3옥타헤드라			Fd3m	[[3[4]]]	2+:2	2*32
{3,9}	이코사면체 1개 옥타헤드라 2개			I3	[[4,3+,4]]	8°:2	22*2
{3,12}	옥타헤드라 5개			임3m	[[4,3,4]]	8°:2	2*32

프리즘 형태

프리즘 형식: {4,5}

두 가지 프리즘 형태가 있다.

1. {4,5}: 꼭지점에 있는 5개의 정사각형(입방 구멍으로 연결된 2개의 평행 정사각형 기울기)
2. {3,8: 꼭지점에 있는 8개의 삼각형(팔면 구멍으로 연결된 2개의 평행 삼각형 기울기)

기타 양식

또한, {3,10}은 삼각형 기울기의 평행 평면에서 형성되며, 서로 교차하는 팔면 구멍이 양방향으로 나 있다.

{5,5}은(는) 꼭지점 주위의 3개의 동일 평면 펜타곤과 간격을 채우는 2개의 수직 펜타곤으로 구성된다.

고트는 또한 정기적인 평면 테셀레이션의 다른 주기적인 형태들이 있다는 것을 인정했다.사각 타일링 {4,4} 및 삼각 타일링 {3,6} 모두 3-공간에서 약칭 무한 실린더로 구부릴 수 있다.

정리

그는 몇 가지 정리들을 썼다.

1. 모든 일반 다면체 {p,q}: (p-2)*(q-2)<4.모든 정규 테셀레이션의 경우: (p-2)*(q-2)=4.모든 일반 가성면체: (p-2)*(q-2)>4.
2. 주어진 얼굴을 감싸는 면의 수는 모든 일반화된 다면체에서 p*(q-2)이다.
3. 모든 일반 가성형은 음의 곡선에 가까운 표면에 가깝다.
4. 7개의 정규 가성면체들은 반복적인 구조를 가지고 있다.

균일꼬치아페이로헤드라

다른 많은 유니폼(Vertex-transitive) 꼬치 아페이로헤드라.와흐만, 버트, 클라인만(1974)은 많은 예를 발견했지만 이들의 목록이 완전한지는 알려지지 않았다.

여기에 몇 가지 삽화가 있다.스큐 형태에 대한 고유한 명칭은 아니지만, 정점 구성에 의해 이름이 지정될 수 있다.

균일한 꿀벌과 관련된 균일한 꼬치 아페이로헤드라

4.4.6.6		6.6.8.8
캔티트런 큐빅 벌집과 관련하여,		런시코틱 큐빅 벌집과 관련된,
4.4.4.6	4.8.4.8	3.3.3.3.3.3.3
전분해 세제곱 벌집과 관련:
4.4.4.6	4.4.4.8	3.4.4.4.4
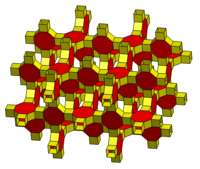		런시트가 달린 큐빅 벌집과 관련이 있다.

프리즘 균일 스큐 아페이로헤드라

4.4.4.4.4	4.4.4.6
관련	관련

다른 것들은 다면체의 강화된 사슬로 구성될 수 있다.

유니폼 보어디크-콕시터나선	정육면체

참고 항목

• 페트리 폴리곤
• 일반 스큐 다면체

참조

• Coxeter, 일반 폴리토페스, 제3판, (1973) 도버판, ISBN0-486-61480-8
• 케일리디스코어: H.S.M. Coxeter의 선별된 글, F가 편집한 글.아서 셔크, 피터 맥멀런, 앤서니 C.Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN978-0-471-01003-6[2]
  • (용지 2) H.S.M. Coxeter, "일반 해면체 또는 스큐 폴리헤드라", Scripta Mathematica 6 (1939) 240-244.
• 존 H. 콘웨이, 하이디 버기엘, 채임 굿맨-스트라우스, (2008) 사물의 대칭성, ISBN 978-1-56881-220-5 (23장, 프라임 대칭성을 가진 객체, 사이비 플라톤 다면체, p340-344)
• Schulte, Egon (2004), "Chiral polyhedra in ordinary space. I", Discrete and Computational Geometry, 32 (1): 55–99, doi:10.1007/s00454-004-0843-x, MR 2060817. [3]
• A. F. Wells, 3차원 네트와 Polyedra, Wiley, 1977.[4]
• A. 워치만, M. 버트와 M. 클라인만, 인피니트 폴리헤드라, 테크니온, 1974. 제2회 Edn. 2005.
• E. Schulte, J.M. Wills On Coxeter의 정규 스큐 다면체, 이산수학, 60권, 6월-1986년 7월 페이지 253-262

외부 링크

• Weisstein, Eric W. "Regular Skew Polyhedron". MathWorld.
• Weisstein, Eric W. "Honeycombs and sponges". MathWorld.
• Olshevsky, George. "Skew polytope". Glossary for Hyperspace. Archived from the original on 4 February 2007.
• "하이퍼볼릭" 테셀레이션스
• 무한정 일반 다면체 [5]
• 무한반복 다면체 - 3공간의 부분 허니컴
• 18 다면체 및 다면체의 대칭성, Egon Schulte: 18.3 일반 다면체
• 무한 폴리헤드라, T.E. 도로진스키