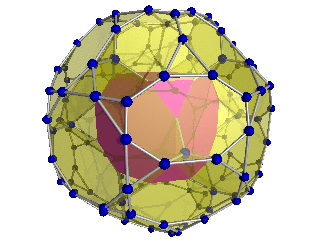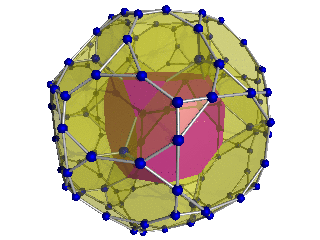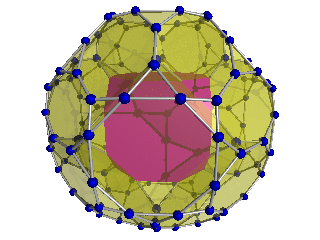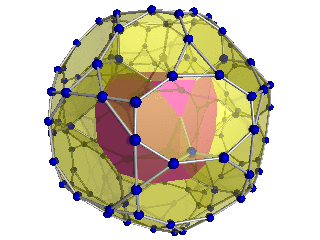
잘린 24셀

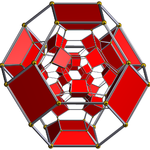24셀	잘린 24셀	비트런티드 24셀
슐레겔 도표는 1 [3,4]를 중심으로 한다([4,3]의 반대쪽에 있는 셀)

기하학에서 잘린 24셀은 일반 24셀의 잘림으로 형성된 균일한 4폴리토프(4차원 균일한 폴리토프)이다.

두 개의 절개 정도가 있는데, 여기에는 약간의 절개도 포함된다.

잘린 24셀

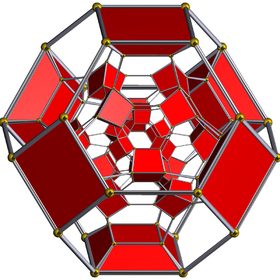슐레겔 도표
잘린 24셀
유형	제복4폴리토프
슐레플리 기호	t{3,4,3} tr{3,3,4}= $t\left\{{\begin{array}{l}3\\3,4\end{array}}\right\}$ $t\left\{{\begin{array}{l}3\\3,4\end{array}}\right\}$ , $t\left\{{\begin{array}{l}3\\3,4\end{array}}\right\}$ 4 $t\left\{{\begin{array}{l}3\\3,4\end{array}}\right\}$ } ${\$ {array $}{l}3\\\3,4\end{array}\right\}}}}}}$ t{3^1,1,1} = $t\left\{{\begin{array}{l}3\\3\\3\end{array}}\right\}$ $t\left\{{\begin{array}{l}3\\3\\3\end{array}}\right\}$ $t\left\{{\begin{array}{l}3\\3\\3\end{array}}\right\}$ $t\left\{{\begin{array}{l}3\\3\\3\end{array}}\right\}$ ${\$ array}{ $l}3\\3\end{array}\right\}}}}}$
콕시터 다이어그램
세포	48	24 4.6.6 24 4.4.4
얼굴	240	144 {4} 96 {6}
가장자리	384
정점	192
정점수	등각 삼각 피라미드
대칭군	F₄ [3,4,3], 1152 주문
회전 부분군	[3,4,3]⁺ 주문 576
정류자 부분군	[3⁺,4,3⁺], 주문 288
특성.	볼록하게 하다
균일지수	23 24 25

잘린 24세포 또는 잘린 이코시테트라초론은 48세포: 24큐브, 24잘린 옥타헤드라로 경계된 균일한 4차원 폴리토프(또는 균일한 4-폴리토프)이다.각 꼭지점은 3개의 잘린 옥타헤드라와 1개의 정육면체를 정삼각형 피라미드 정점으로 연결한다.

건설

잘린 24-셀은 다음과 같은 세 가지 대칭 그룹을 가진 폴리탑으로 구성될 수 있다.

F₄ [3,4,3]: 24-셀의 잘림.
B₄ [3,3,4]: 잘린 팔면세포의 두 패밀리가 있는 16-셀의 캔트런지.
D₄ [3^1,1,1]: 잘린 팔면세포의 세 집단이 있는 탈면체의 잡식성.

콕시터군	${F}_{4}$ ${F}_{4}$ ${\$ ${F}_{4}$ = [3,4,3]	${C}_{4}$ ${C}_{4}$ ${\$ ${C}_{4}$ = [4,3,3]	${D}_{4}$ ${D}_{4}$ ${\$ ${D}_{4}$ = [3,3^1,1]
슐레플리 기호	t{3,4,3}	tr{3,4}	t{3^1,1,1}
주문	1152	384	192
가득찬 대칭 무리를 짓다	[3,4,3]	[4,3,3]	<[3,3^1,1]> = [4,3,3] [3[3^1,1,1]] = [3,4,3]
콕시터 다이어그램
면	3: 1:	2: 1: 1:	1,1,1: 1:
정점수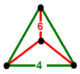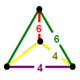

조노토프

또한 조노토프(Zonotope): 벡터의 12행(+1,-1,0,0) 중 반대 쌍을 연결하는 6행 세그먼트의 민코우스키 합으로 형성할 수 있다.

데카르트 좌표, 평행 좌표.

가장자리 길이 sqrt(2)가 있는 잘린 24-셀 정점의 데카르트 좌표는 모두 좌표 순열과 부호 조합이다.

(0,1,2,3) [4!×2³ = 192 정점]

이중 구성에는 모든 좌표 순열에서 좌표가 있고

(1,1,1,5) [4×2⁴ = 64 꼭지점]

(1,3,3) [4×2⁴ = 64 꼭지점]

(2,2,2,4) [4×2⁴ = 64 꼭지점]

구조

24개의 정사각형 세포는 사각형을 통해 잘린 옥타헤드라에 연결되고 24개의 잘린 옥타헤드라는 육각형 표면을 통해 서로 연결된다.

투영

잘린 24-셀을 3차원 공간으로 병렬 투영한 후, 먼저 잘린 8각형(Octavedron)

투영 봉투는 잘린 칸옥타헤드론이다.
잘린 옥타헤드라의 두 개가 봉투 중앙에 놓여 있는 잘린 옥타헤드론에 투영된다.
6개의 입체본이 이 중앙의 잘린 팔면체의 네모난 면과 거대한 롬비쿠옥타면체의 팔각면 중앙을 잇는다.이것들은 각 이미지에 한 쌍의 세포인 12개의 입체 세포의 이미지들이다.
거대한 롬비큐옥타헤드론의 12개의 사각형 면은 나머지 12개의 정육면체의 모습이다.
대롬비옥타헤드론의 6각형 면은 잘린 옥타헤드라의 6각형이다.
투영 봉투의 육각형 면과 중앙 잘린 팔면 사이에 놓여 있는 8(균일하지 않은) 잘린 팔면적은 나머지 16개의 잘린 팔면이며, 각 이미지에 한 쌍의 셀이다.

이미지들

맞춤법 투사
콕시터 평면	F₄
그래프
치측 대칭	[12]
콕시터 평면	B₃ / A₂ (a)	B₃ / A₂ (b)
그래프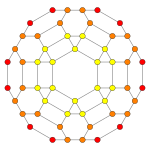
치측 대칭	[6]	[6]
콕시터 평면	B₄	B₂ / A₃
그래프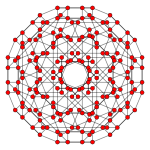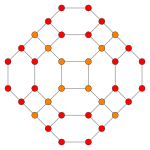
치측 대칭	[8]	[4]

슐레겔 도표 (세포를 볼 수 있음)	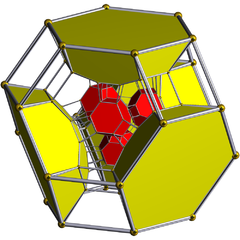슐레겔 도표 24개의 잘린 팔면 세포 중 8개가 보인다.
입체 투영법 잘린 사면체 중심

그물
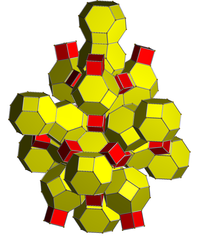잘린 24셀	이중에서 24-셀 절단

비트런티드 24셀

비트런티드 24셀
대체 셀이 숨겨져 있는 잘린 큐브 중심의 슐레겔 다이어그램
유형	제복4폴리토프
슐레플리 기호	2t{3,4,3}
콕시터 다이어그램
세포	48 (3.8.8)
얼굴	336	192 {3} 144 {8}
가장자리	576
정점	288
에지 피겨	3.8.8
정점수	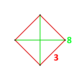사방형 분산형
이중 폴리토프	디스페노이드 288 셀
대칭군	자동(F₄), [3,4,3], 주문 2304
특성.	볼록, 이소간, 동위원소, 이소차리학
균일지수	26 27 28

그물

24-셀을 약간 잘라낸 것. 48-셀, 또는 테트라콘톡타코론은 24-셀에서 파생된 4차원 균일한 폴리토프(또는 균일한 4-폴리토프)이다.

E. L. Elte는 1912년에 그것을 반정형 폴리토프로 확인했다.

그것은 24-셀을 비트런팅(듀얼 24-셀을 산출할 수 있는 깊이의 중간에서 트런캐스팅)으로 구성된다.

균일한 4폴리토프로서, 그것은 정점 변환이다.또한 세포 전이성이며, 잘린 정육면체 48개로 구성되어 있으며, 또한 가장자리당 3개의 잘린 정육면체 세포가 있고, 각 가장자리 둘레에 1개의 삼각형, 2개의 옥타곤이 있다.

24-셀의 48개 세포는 24-셀의 24개 세포와 24 정점에 해당한다.이와 같이 48개 세포의 중심은 F형의₄ 뿌리계를 형성한다.

그것의 정점 수치는 4각형 분산형이며, 2개의 반대쪽 가장자리 길이 1과 4개의 가장자리 길이가 모두 2개(2+2), 4개의 가장자리 길이가 모두 있는 4면체다.

대체 이름

24-셀 비트런드(Norman W. Johnson)
세포변환 4-148로 48세포
비트런드 이코시테트라초론
비트런드 폴리옥타헤드론
테트라콘타옥타초론 (콘텐트) (조나단 바우어스)

구조

잘린 정육면체는 팔각면을 통해 반대 방향으로 서로 연결된다. 즉, 인접한 두 개의 잘린 정육면체는 서로에 대해 45도 회전하여 두 개의 삼각형 면이 모서리를 공유하지 않도록 한다.

잘린 정육면체의 순서는 8개의 순환을 이룬다.잘린 각 입방체는 그러한 3개의 주기에 속한다.반면에, 잘린 정육면체의 순서는 반대 삼각형 면을 통해 서로 연결되어 6의 주기를 이룬다.잘린 각 입방체는 그러한 4개의 사이클에 속한다.

구성 매트릭스에서 볼 수 있듯이 요소 사이의 모든 발생 횟수가 표시된다.대각선 f-벡터 번호는 Wythoff 구조를 통해 도출되며, 한 번에 하나의 거울을 제거하여 서브그룹 주문의 전체 그룹 순서를 나눈다.가장자리는 4개의 대칭 위치에 있다.정사각형은 3개 위치, 육각형은 2개 위치, 8각형은 1개 위치에 있다.마지막으로 기본 심플렉스 4개 모서리를 중심으로 4종류의 세포가 존재한다.^[1]

F₄	k-face	f_k	f₀	f₁		f₂			f₃		크-피규격	메모들
A₁A₁	( )	f₀	288	2	2	1	4	1	2	2	s{2,4}	F₄/A₁A₁ = 288
	{ }	f₁	2	288	*	1	2	0	2	1	{ }v( )
	{ }	f₁	2	*	288	0	2	1	1	2	{ }v( )
A₂A₁	{3}	f₂	3	3	0	96	*	*	2	0	{ }	F₄/A₂A₁ = 1152/6/2 = 96
B₂	t{4}		8	4	4	*	144	*	1	1		F₄/B₂ = 1152/8 = 144
A₂A₁	{3}		3	0	3	*	*	96	0	2		F₄/A₂A₁ = 1152/6/2 = 96
B₃	t{4,3}	f₃	24	24	12	8	6	0	24	*	( )	F₄/B₃ = 1152/48 = 24
B₃	t{4,3}	f₃	24	12	24	0	6	8	*	24	( )	F₄/B₃ = 1152/48 = 24

좌표

가장자리 길이 2를 갖는 24-셀의 비트가 있는 데카르트 좌표는 모두 좌표 순열과 다음 부호의 표식이다.

(0, 2+√2, 2+√2, 2+2√2)

(1, 1+√2, 1+√2, 3+2√2)

투영

2차원으로 투영

맞춤법 투사
콕시터 평면	F₄	B₄
그래프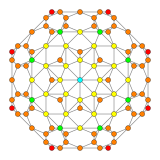
치측 대칭	[[12]] = [24]	[8]
콕시터 평면	B₃ / A₂	B₂ / A₃
그래프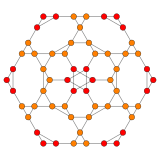
치측 대칭	[6]	[[4]] = [8]

3차원으로 투영

직교	원근법
다음 애니메이션은 24-셀을 3차원으로 비트롤링한 직교 투영을 보여준다.애니메이션 자체는 정적 3D 영상에서 2D로 투영되는 원근 투영법이며, 그 구조를 더욱 뚜렷하게 하기 위해 회전이 추가된다. 48개의 잘린 정육면체의 이미지는 다음과 같이 배열된다. 중앙 잘린 큐브는 4D 관점에 가장 가까운 셀로, 보기 쉽게 강조 표시된다.시각적 혼란을 줄이기 위해 이 중앙 잘린 큐브에 있는 정점과 가장자리가 생략되었다. 이 중앙 잘린 정육면 주위에는 팔각면을 통해 6개의 잘린 정육면체가 부착되어 있고, 삼각면을 통해 8개의 잘린 정육면체가 부착되어 있다.이 세포들은 중앙 세포가 보이도록 투명하게 만들어졌다. 투영 봉투의 바깥쪽 네모난 면은 6개의 잘린 정육면체의 이미지이고, 투영 봉투의 12개의 길쭉한 팔각면은 12개의 잘린 정육면체의 이미지다. 나머지 셀은 24-셀을 잘라낸 끝에 놓여 있고 4D 시각에서 가려져 있기 때문에 도태되었다.여기에는 강조 표시된 잘린 입방체와 동일한 부피로 투영되었을 대척점 잘린 입방체가 포함되며, 8개의 잘린 입방체가 팔각면을 통해 부착되고, 잘린 입방체를 둘러싼 8개의 잘린 입방체가 삼각면을 통해 부착된다.	다음 애니메이션은 24-셀을 3차원으로 비트런딩한 셀의 첫 번째 투시 투영을 보여준다.원근 투영으로 인해 일부 단축이 있다는 점을 제외하면 이전 애니메이션과 구조는 동일하다.

입체 투영법

디스페노이드 288 셀

디스페노이드 288 셀
유형	완벽한^[2] 폴리초론
기호	f_1,2F₄^[2] (1,0,0,0)_F₄ ⊕ (0,0,0,1)_F₄^[3]
콕시터
세포	288개의 콘그루엔트 4각형 디스페노이드
얼굴	576개의 합체 이소체 (2개의 짧은 가장자리)
가장자리	336	$\scriptstyle 1$ 1 ${\$ 의 192개 길이 $\scriptstyle {\sqrt {2-{\sqrt {2}}}}$ - $\scriptstyle {\sqrt {2-{\sqrt {2}}}}$ ${\$ 2}}:}
정점	48
정점수	(트리아키스 옥타헤드론)
이중	비트런티드 24셀
콕시터군	자동(F₄), [3,4,3], 주문 2304
궤도 벡터	(1, 2, 1, 1)
특성.	볼록한, 이소차리의

분산형 288-셀은 24-셀의 이중이다.24세포에서 파생된 4차원 폴리토프(혹은 폴리초론)이다.24셀을 두 배로 회전시킨 뒤 볼록한 선체를 건조하는 방식이다.

균일한 폴리초론의 이중으로, 288개의 콘그루엔트 4각형 디스패노이드로 구성된 세포 변환이다.또한, Aut(F₄) 그룹에서는 정점 변환이다.^[3]

이미지들

직교 투영
콕시터 평면	B₂	B₃	F₄
디스페노이드 288 셀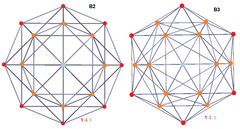
비트런어드 24셀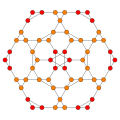

기하학

288 셀의 정점은 정확히 표준 제곱 1을 가진 24 허위츠 유닛 쿼터니온이고, 3-sphere 유닛에 투영된 표준 제곱 2를 가진 듀얼 24 셀의 정점과 결합된다.이 48 정점들은 이진 팔면 그룹 2O 또는 <2,3,4>, 순서 48에 해당한다.

Thus, the 288-cell is the only non-regular 4-polytope which is the convex hull of a quaternionic group, disregarding the infinitely many dicyclic (same as binary dihedral) groups; the regular ones are the 24-cell (≘ 2T or <2,3,3>, order 24) and the 600-cell (≘ 2I or <2,3,5>, order 120).(16-셀은 2진수₂ 2D 또는 <2,2,2>, 순서 16에 해당한다.)

새겨진 3-sphere는 반경 1/2+2/4 4 0.853553을 가지며 이중 비트코인 24-셀의 정점인 288 테트라헤드라의 중심에 있는 288-셀에 닿는다.

정점은 빨간색과 노란색이라고 하는 두 가지 색상으로 색칠할 수 있으며, 24개의 허위츠 유닛은 빨간색으로, 24개의 듀얼은 노란색으로, 24개의 셀은 빨간 색과 일치한다.따라서 동일한 색상의 쿼터니온 2개의 제품은 빨간색이고 혼합 색상의 2개의 제품은 노란색이다.

지역	층	위도	적색의		노랑색의
북반구	3	1	1	$1$	0
	2	√2/2	0		6	${\tfrac {\sqrt {2}}:\\\;\;1\pm \mathrm {i},\;\;1\pm \mathrm {j},\;\;\;1\mathrm {k} \}}}}}}}}}}}$
	1	1/2	8	${\tfrac {1}{1}:{1\pm \mathrm {i}pm \mathrm {j}pm \mathrm {k} \}}}$	0
적도	0	0	6	$\{\pm \mathrm {i},\pm \mathrm {j},\pm \mathrm {k} \}}}$	12	${\tfrac{\2}}\{\,\pm \mathrm {i}pm \mathrm {j},\pm \mathrm {i}pm \mathrm {k},\pm \mathrm {j} \matrmatrmathrm {k} \k} \k} \k} \k} \k}}}}}}}}}}}}}}}}}}}}}}}}}}}}$
남반구	–1	–1/2	8	$-{\tfrac {1}{1}:{1\pm \mathrm {i}pm \mathrm {j}pm \mathrm {k} \}}}$	0
	–2	–√2/2	0		6	${\tfrac {\sqrt {2}}:\{-1\pm \mathrm {i},-1\pm \mathrm {j},-1\pm \mathrm {k} \}}}}}}$
	–3	–1	1	$-1$	0
합계			24		24

북극(1,0,0,0)에 고정된 적색 꼭지점을 배치하면 (2/2,x,y,z)에서 다음으로 더 깊은 "위도"에 6개의 황색 꼭지점이 있고, 그 다음에 위도(1/2,x,y,z)에서 8개의 적색 꼭지점이 있다.전체 좌표는 $1,\mathrm {i} ,\mathrm {j} ,\mathrm {k}$ 쿼터니온 $1,\mathrm {i} ,\mathrm {j} ,\mathrm {k}$ 1, i $1,\mathrm {i} ,\mathrm {j} ,\mathrm {k}$ , $1,\mathrm {i} ,\mathrm {j} ,\mathrm {k}$ , $1,\mathrm {i} ,\mathrm {j} ,\mathrm {k}$ , k $1,\mathrm {i} ,\mathrm {j} ,\mathrm {k}$ , k {\ $displaystyle$ 1 $,\mathrm {i} ,\mathrm {j} ,\mathrm {k}}$ 의 선형 조합으로 주어지며 $1,\mathrm {i} ,\mathrm {j} ,\mathrm {k}$ 동시에 그룹 2O의 요소로 삼을 수 있다.다음 더 깊은 위도는 적도 하이퍼플레인이 2-sphere에서 3-sphere를 교차하는 것으로, 6개의 적색 정점과 12개의 황색 정점으로 채워진다.

레이어 2는 가장자리의 길이가 1인 일반 팔면체를 2-sphere로 묶는 것이다.북극의 꼭지점이 있는 4면체에는 긴 가장자리로 1개의 가장자리가 있으며, 두 개의 꼭지점이 짧은 가장자리로 북극에 연결되어 있다.또 다른 긴 가장자리는 북극에서 1층으로, 2층에서 2층으로 이어진다.

동일한 색상을 연결하는 길이 1의 긴 가장자리 192개와 길이 2–2 ≈ 0.765367의 짧은 가장자리 144개가 있다. 192*2/48 = 8 길이, 144*2/48 = 6개의 짧은 가장자리가 있으며, 144개의 가장자리는 모든 꼭지점에서나 만난다.

576개의 면은 길이가 1개, 짧은 2개의 가장자리가 있는 등각형이며, 모두 합치된다.베이스의 각도는 아르코(√4+/8/4) 2 49.210°576*3/48 = 36개의 얼굴이 정점에서 만나고, 576*1/3 = 긴 가장자리, 576*2/8 = 짧은 가장자리에서 만난다.

288개의 세포는 4개의 짧은 가장자리와 2개의 반향 긴 가장자리와 수직 긴 가장자리로 이루어져 있으며, 그 중 하나는 붉은색 2개와 다른 2개의 노란 정점을 연결한다.모든 세포가 일치한다.288*4/48 = 24개의 세포가 정점에서 만난다. 288*2/4 = 3개의 세포는 긴 가장자리에서 만난다. 288*4/4/8 = 짧은 가장자리에서 만난다.288*4/576 = 2개의 세포가 삼각형에서 만난다.

참조

^ Klitzing, Richard. "o3x4x3o - cont".
^ ^a ^b 완벽한 4-폴리토페즈 Gabor Gévay 대수 및 기하학에 대한 기여 43 (2002), 1번, 243-259 ] 표 2, 252페이지
^ ^a ^b Quaternionic Construction of the W(F4) Polytopes with Their Dual Polytopes and Branching under the Subgroups W(B4) and W(B3) × W(A1) Mehmet Koca 1, Mudhahir Al-Ajmi 2 and Nazife Ozdes Koca 3 Department of Physics, College of Science, Sultan Qaboos University P. O. Box 36, Al-Khoud 123, Muscat, Sultanate of Oman, p.18. 5.7 Dual polytope of the polytope(0, 1, 1, 0)F₄ = W(F₄)(Ω₂+Ω₃)

H.S.M. Coxeter:
- 케일리디스코어: H.S.M. Coxeter의 선별된 글, F가 편집한 글.아서 셔크, 피터 맥멀런, 앤서니 C.Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  - (용지 22) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 I, [산술]Zeit. 46 (1940) 380-407, MR 2,10]
  - (용지 23) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 II, [수학]Zeit. 188 (1985) 559-591]
  - (용지 24) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 III, [산술]Zeit. 200 (1988) 3-45]
Norman JohnsonUniform Polytopes, 원고(1991)
- N.W. 존슨:균일다각체와 허니컴의 이론, 박사 (1966)
Klitzing, Richard. "4D uniform polytopes (polychora)". x3x4o3o=x3x3x4o - tico, o3x3o - cont
3. icositetrachoron(24세포)을 기반으로 한 볼록한 균일한 폴리초라 - 모델 24, 27, 조지 올셰프스키

[1] Klitzing, Richard. "o3x4x3o - cont".

[Gevay-2] 완벽한 4-폴리토페즈 Gabor Gévay 대수 및 기하학에 대한 기여 43 (2002), 1번, 243-259 ] 표 2, 252페이지

[Koca-3] Quaternionic Construction of the W(F4) Polytopes with Their Dual Polytopes and Branching under the Subgroups W(B4) and W(B3) × W(A1) Mehmet Koca 1, Mudhahir Al-Ajmi 2 and Nazife Ozdes Koca 3 Department of Physics, College of Science, Sultan Qaboos University P. O. Box 36, Al-Khoud 123, Muscat, Sultanate of Oman, p.18. 5.7 Dual polytope of the polytope(0, 1, 1, 0)F₄ = W(F₄)(Ω₂+Ω₃)

[1]

[2]

[3]

D₄ 균일 폴리초라


{3,3^1,1} h{4,3,3}	2r{3,3^1,1} h₃{4,3,3}	t{3,3^1,1} h₂{4,3,3}	2t{3,3^1,1} h_2,3{4,3,3}	r{3,3^1,1} {3^1,1,1}={3,4,3}	rr{3,3^1,1} r{3^1,1,1}=r{3,4,3}	tr{3,3^1,1} t{3^1,1,1}=t{3,4,3}	sr{3,3^1,1} s{3^1,1,1}=s{3,4,3}

B4 대칭 폴리탑
이름	큐테릭트	수정한 큐테릭트	잘린 큐테릭트	알 수 있는 큐테릭트	녹이 슨 큐테릭트	굵게 깎인 큐테릭트	칸트런이 있는 큐테릭트	구김살이 있는 큐테릭트	다량의 큐테릭트
콕시터 도표를 만들다		=				=
슐레플리 심볼	{4,3,3}	t₁{4,3,3} r{4,3,3}	t_0,1{4,3,3} t{4,3,3}	t_0,2{4,3,3} rr{4,3,3}	t_0,3{4,3,3}	t_1,2{4,3,3} 2t{4,3,3}	t_0,1,2{4,3,3} tr{4,3,3}	t_0,1,3{4,3,3}	t_0,1,2,3{4,3,3}
슐레겔 도표를 만들다
B₄

이름	16 셀	수정한 16 셀	잘린 16 셀	알 수 있는 16 셀	녹이 슨 16 셀	굵게 깎인 16 셀	칸트런이 있는 16 셀	구김살이 있는 16 셀	다량의 16 셀
콕시터 도표를 만들다	=	=	=	=		=	=
슐레플리 심볼	{3,3,4}	t₁{3,3,4} r{3,3,4}	t_0,1{3,3,4} t{3,3,4}	t_0,2{3,3,4} rr{3,4}	t_0,3{3,3,4}	t_1,2{3,3,4} 2t{3,4}	t_0,1,2{3,3,4} tr{3,4}	t_0,1,3{3,3,4}	t_0,1,2,3{3,3,4}
슐레겔 도표를 만들다
B₄

24-셀 계열 폴리토페스
이름	24셀	잘린 24셀	24셀을 훔치다	정류 24세포	24세포로 알 수 있는	24구경.	캔트런 24셀	윤택 24셀	24구경.	전지 24셀
슐레플리 심볼	{3,4,3}	t_0,1{3,4,3} t{3,4,3}	s{3,4,3}	t₁{3,4,3} r{3,4,3}	t_0,2{3,4,3} rr{3,4,3}	t_1,2{3,4,3} 2t{3,4,3}	t_0,1,2{3,4,3} tr{3,4,3}	t_0,3{3,4,3}	t_0,1,3{3,4,3}	t_0,1,2,3{3,4,3}
콕시터 도표를 만들다
슐레겔 도표를 만들다
F₄
B₄
B₃(a)
B₃(b)
B₂

Search

잘린 24셀

네임스페이스

더

목차

잘린 24셀

건설

조노토프

데카르트 좌표, 평행 좌표.

구조

투영

이미지들

관련 폴리토페스

비트런티드 24셀

대체 이름

구조

좌표

투영

2차원으로 투영

3차원으로 투영

관련정규다면체

디스페노이드 288 셀

이미지들

기하학

관련 폴리토페스

참조