런케이티드 5-셀

A₄ Coxeter 평면의 직교 투영
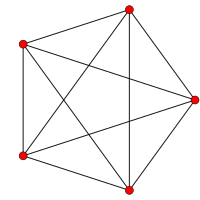5세포	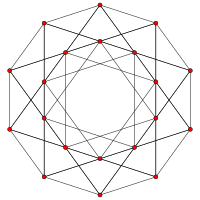런케이티드 5-셀
런시트드 5셀	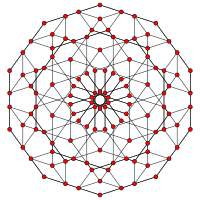옴니트런드 5세포 (Runcicantitruntrunced 5-cell)

4차원 기하학에서 런케이티드 5-셀은 볼록한 균일 4-폴리토프로서 일반 5-셀의 런케이팅(세 번째 순서 절단, 얼굴 계획까지)이다.

5-셀에는 순열, 줄임, 그리고 운율을 포함하여 3개의 독특한 운율이 있다.

런케이티드 5-셀

런케이티드 5-셀
사면세포의 절반이 보이는 슐레겔 도표.
유형	제복4폴리토프
슐레플리 기호	t_0,3{3,3,3}
콕시터 다이어그램	또는 또는
세포	30	10 (3.3.3) 20 (3.4.4)
얼굴	70	40 {3} 30 {4}
가장자리	60
정점	20
정점수	(등각삼각형 항정신병)
대칭군	자동(A₄), [3,3,3], 주문 240
특성.	볼록, 이등분 동위원소
균일지수	4 5 6

런케이티드 5셀 또는 작은 프리즘태코론은 반경방향으로 5셀의 세포를 확장하고 삼각 프리즘(얼굴 프리즘과 가장자리 그림)과 테트라헤드라(듀얼 5셀의 셀)로 간격을 메우는 방식으로 구성된다.4면체 10개와 삼각형 프리즘 20개로 구성되어 있다.10개의 4면체는 5세포의 세포와 그것의 이중과 일치한다.

지형학적으로, 그것의 가장 높은 대칭인 [3,3,3] 아래에는 오직 하나의 기하학적 형태만이 있는데, 10개의 사면체 및 20개의 균일한 삼각형 프리즘을 포함하고 있다.직사각형은 두 쌍의 가장자리가 확장된 대칭 아래에서 동일하게 만들어진 5개의 정규 4차 테트라 두 세트의 가장자리에 각각 해당하기 때문에 항상 정사각형이다.

E. L. Elte는 1912년에 그것을 반정형 폴리토프로 확인했다.

대체 이름

런케이티드 5-셀(노먼 존슨)
런케이티드 펜타초론
런케이티드 4-심플렉스
확장된 5-셀/4-심플렉스/펜타코론
작은 프리즘아테카초론 (Acronim: Spid) (Jonathan Bowers)

구조

사면세포 10개 중 2개가 각 꼭지점에서 만난다.삼각형의 프리즘은 그들 사이에 놓여 있고, 삼각형의 얼굴에 의해 연결되어 있고, 사각형의 얼굴에 의해 서로 연결되어 있다.각 삼각형 프리즘은 반방향으로 인접한 삼각형 프리즘에 결합된다(즉, 공유 사각형의 가장자리 A와 B가 하나의 프리즘의 삼각형 면에 결합되는 경우 다른 두 개의 가장자리로 다른 프리즘의 삼각형 면에 결합된다). 따라서 각 인접한 프리즘 쌍은 동일한 하이퍼플라로 회전하는 경우 각 쌍의 프리즘을 결합한다.네, 교비파스티기움을 형성할 겁니다

해부

윤활유 5세포는 중앙 큐보타헤드론에 의해 두 개의 사면 큐폴라로 해부될 수 있다.이 절개는 중앙 육각형에 의해 두 개의 삼각형 큐폴라로 해부되는 3D 큐옥타헤드론과 유사하다.

이미지들

맞춤법 투사
A을_k 콕시터 평면	A을₄	A을₃	A을₂
그래프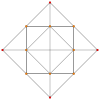
치측 대칭	[[5]] = [10]	[4]	[[3]] = [6]

10개의 사면세포가 있는 3-sphere 투영 슐레겔 다이어그램 내부 보기	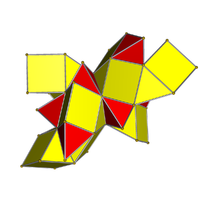그물

좌표

가장자리 길이 2의 원점 중심 런케이티드 5-셀 정점의 데카르트 좌표는 다음과 같다.

$\pm \left\sqrt{5}{2}}:\\frac {1}{\sqrt{6}}}}\\frac {1}{\sqrt{3}}}\pm 1\오른쪽)$ $\pm \left\sqrt{5}{2}}:\\frac {1}{1}{\sqrt{6}}}\\\frac {-2}{\sqrt{3}}}}\오른쪽)$ $\pm \left\sqrt {\frac {5}{2}}:},\\sqrt {\frac {3}{3}}},\ 0\ 오른쪽)$	$\pm \left(0,\ 2{\sqrt {2}{3}}},\\pm 1\오른쪽)$ $\pm \left(0,\ 2{\sqrt {2}{3}}},\\frac {-2}{\sqrt {3}},\ 0\오른쪽)$ ${\displaystyle \left(0,\0,\\pm {3},\pm 1\오른쪽)$ $\left(0,\ 0,\ 0,\\\pm 2\오른쪽)$

다음과 같은 20개의 순열로 5-공간에서 보다 단순한 좌표 세트를 만들 수 있다.

(0,1,1,1,2)

이 구조는 런민 5정맥의 32정형 면 중 하나로 존재한다.

정류된 5정맥의 중심에서 5정맥의 두 번째 시공은 다음과 같은 좌표 순열로 주어진다.

(1,-1,0,0,0)

루트 벡터

그것의 20개의 꼭지점은 단순 리 그룹 A의₄ 루트 벡터를 나타낸다.그것은 또한 4-공간에서 5-셀 벌집모양의 꼭지점이다.

횡단면

3차원 하이퍼플레인(hyperplane)을 가진 런케이티드 5셀의 최대 단면은 큐폭타헤드론이다.이 단면에서는 각 5개의 테트라헤드라와 10개의 삼각 프리즘으로 구성된 2개의 사면체 고컵극으로 나뉜다.

투영

런케이티드 5셀을 3차원 공간으로 4면체 먼저 직교로 투영한 것은 큐옥타헤드럴 봉투를 가지고 있다.이 투영의 구조는 다음과 같다.

큐옥타이드 봉투는 내부적으로 다음과 같이 나뉜다.

납작한 사면체 4개는 큐옥타면체의 삼각형 면 중 4개를 중심 사면체에 접합한다.이것들은 4면체 세포 중 5개의 이미지들이다.
육면체의 6개의 정사각형 면은 일그러진 삼각 프리즘을 통해 중앙 사면체의 가장자리에 연결된다.이것들은 삼각 프리즘 세포 중 6개의 이미지들이다.
나머지 4개의 삼각형 면은 4개의 삼각 프리즘(투영에 의해 왜곡됨)을 통해 중앙 사면체에 연결된다.이것들은 삼각형 프리즘 세포 중 또 다른 4개의 이미지들이다.
이는 '북반구'라고 생각할 수 있는 5세포(사면체 5개, 삼각형 프리즘 10개)의 절반을 차지한다.

나머지 절반인 '남반구'는 이중 방향의 큐보타헤드론의 이형성 분할에 해당하며, 이 경우 중앙 사면체는 상반기에 이형이다.큐옥타헤드론의 삼각형 면은 한 반구의 삼각형 프리즘과 결합하여 다른 반구의 평평한 사트라헤드라를 이루며, 그 반대도 마찬가지다.따라서 남반구는 또 다른 5개의 4각형 프리즘과 10개의 3각형 프리즘을 포함하고 있어 총 10개의 4각형 프리즘과 20개의 3각형 프리즘을 이루고 있다.

런시트드 5셀

런시트드 5셀
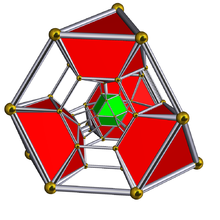슐레겔 다이어그램 표시된 칸옥타헤드랄 세포
유형	제복4폴리토프
슐레플리 기호	t_0,1,3{3,3,3}
콕시터 다이어그램
세포	30	5 (3.6.6) 10 (4.4.6) 10 (3.4.4) 5 (3.4.3.4)
얼굴	120	40 {3} 60 {4} 20 {6}
가장자리	150
정점	60
정점수	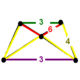(직사각형 피라미드)
콕시터군	A₄, [3,3,3], 120개 주문
특성.	볼록, 이등변
균일지수	7 8 9

그물

5-셀 또는 프리즘토르혼방 펜타코론은 정점 60개, 가장자리 150개, 면 120개, 셀 30개로 구성된다.세포는 잘린 사트라헤드라 5개, 육각 프리즘 10개, 삼각 프리즘 10개, 큐보타헤드라 5개 등이다.각 꼭지점은 잘린 사면체, 육각형 프리즘, 삼각형 프리즘, 큐옥타면체 등 5개의 세포로 둘러싸여 있으며, 정점 모양은 직사각형 피라미드형이다.

대체 이름

런티런드 펜타코론
런시트드림 4-심플렉스
디프리스마토덴타초론
프리즘토르혼합 펜타코론 (아크로니어: prip) (조나단 바우어스)

이미지들

맞춤법 투사
A을_k 콕시터 평면	A을₄	A을₃	A을₂
그래프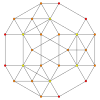
치측 대칭	[5]	[4]	[3]

40개의 파란 삼각형 면과 60개의 초록색 사면이 있는 슐레겔 도표.	슐레겔 도표의 중심 부분.

좌표

에지 길이 2의 원산지 중심 런시트가 있는 5-셀의 데카르트 좌표는 다음과 같다.

좌표
$\left\frac {7}{\sqrt {10}},\\sqrt {3}{2}},\pm {3},\pm 1\오른쪽)$ $\left\frac {7}{\sqrt {10}},\\\sqrt {3}{3}}},\ 0,\\\pm 2\오른쪽)$ $\left\frac {7}{\sqrt {10}},\\frac {-1}{\sqrt {6},\\\frac {2}{\sqrt {3},\pm 2\오른쪽)}$ $\left\frac {7}{\sqrt {10}},\\frac {-1}{\sqrt {6},\\\frac {-4}{\sqrt {3},\ 오른쪽)$ $\left\frac {7}{\sqrt {10}},\\frac {-5}{\sqrt {6},\\\frac {1}{\sqrt {3},\pm 1\오른쪽)}$ $\left\frac {7}{\sqrt {10}},\\frac {-5}{\sqrt {6},\\\frac {-2}{\sqrt {3},\ 오른쪽)$ $\left\sqrt {2}{5}},\pm {\sqrt {6},\pm {3},\pm 1\오른쪽)$ $\left\sqrt {2}{5}},\\pm {6},\0,\\pm 2\오른쪽)$ $\left\sqrt {\frac {2}{5}},\\sqrt {2}{3},\\frac {5}{\sqrt {3},\pm 1\오른쪽)$	$\left\sqrt {\frac {2}{5}},\\sqrt {2}{3},\\frac {-1}{\sqrt {3},\pm 3\오른쪽)$ $\left\sqrt {\frac {2}{5}},\\sqrt {2}{3},\\frac {-4}{\sqrt {3},\pm 2\오른쪽)$ $\left\sqrt {\frac {2}{5}},\\\sqrt {2}{3},\frac {4}{\sqrt {3},\pm 2\오른쪽)$ $\left\sqrt {\frac {2}{5}},\{\\sqrt {2}{3}},\pm 3\right}}}$ $\left\sqrt {\frac {2}{5}},\\\sqrt {2}{3}},\pm 1\pm)$ $\left\frac {-3}{\sqrt {10}},\\frac {5}{\sqrt {6},\\\frac {2}{\sqrt {3},\pm 2\오른쪽)}$ $\left\frac {-3}{\sqrt {10}},\\frac {5}{\sqrt {6},\\\frac {-4}{\sqrt {3},\ 오른쪽)$ $\left\frac {-3}{\sqrt {10}},\\frac {1}{\sqrt {6},\\frac {4}{\sqrt {3},\pm 2\오른쪽)}$ $\left\frac {-3}{\sqrt {10}},\\frac {1}{\sqrt {6},\\frac {1}{\sqrt {3},\pm 3\오른쪽)}$	$\left\frac {-3}{\sqrt {10}},\\frac {1}{\sqrt {6},\\frac {-5}{\sqrt {3},\pm 1\오른쪽)$ $\left\frac {-3}{\sqrt {10}},\\frac {-7}{\sqrt {6},\\\frac {2}{\sqrt {3},\ 오른쪽)$ $\left\frac {-3}{\sqrt {10}},\\frac {-7}{\sqrt {6},\\frac {-1}{\sqrt {3},\pm 1\오른쪽)$ $\left4{\sqrt{2}{5}},\2\sqrt {\frac {2}{3}},\\frac {1}{\sqrt {3},\pm 1\오른쪽)$ $\left4{\sqrt{2}{5}},\2\sqrt {\frac {2}{3}},\\frac {-2}{\sqrt {3},\ 오른쪽)$ ${\displaystyle \left4{\sqrt {2}{5}},\0}\pm {3},\pm 1\오른쪽)$ $\left4{\sqrt {\frac {2}{5}},\ 0,\\\pm 2\오른쪽)$ $\left4}{\sqrt {2}{5}},\2\sqrt {\frac {2}{3}},\\frac {2}{\sqrt {3},\ 오른쪽)$ $\left4}{\sqrt {2}{5}},\2\sqrt {\frac {2}{3}},\\frac {-1}{\sqrt {3}},\오른쪽)$

정점은 다음의 순열처럼 5-공간에서 하이퍼플레인 위에 보다 간단하게 구성할 수 있다.

(0,1,1,2,3)

이 구조는 5정맥의 양성 정사각형 면으로부터 나온 것이다.

옴니트런드 5세포

옴니트런드 5세포
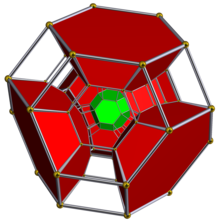잘린 팔면 세포의 절반이 표시된 슐레겔 도표.
유형	제복4폴리토프
슐레플리 기호	t_0,1,2,3{3,3,3}
콕시터 다이어그램	또는 또는
세포	30	10 (4.6.6) 20 (4.4.6)
얼굴	150	90{4} 60{6}
가장자리	240
정점	120
정점수	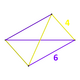식물성 분산체
콕시터군	자동(A₄), [3,3,3], 주문 240
특성.	볼록, 이등변, 조노토프
균일지수	8 9 10

잡동사니 5셀 또는 대 프리즘태코론은 정점 120, 가장자리 240, 면 150(정사각형 90, 육각형 60), 셀 30개로 구성되어 있다.세포는 잘린 옥타헤드라 10개와 육각형 프리즘 20개 입니다.각 꼭지점에는 잘린 옥타헤드라 2개와 육각형 프리즘 2개의 세포가 두 개의 식물성 분산 정점 모양으로 배열되어 있다.

콕세터는 이것을 1906년 저서 <제4차원>에서 설명한 C. H. 힌튼의 이름을 따서 힌튼의 폴리토프라고 부른다.콕세터가 힌튼의 벌집이라고 부르는 균일한 벌집을 형성한다.^[1]

대체 이름

옴니트런드 5세포
옴니트룬드 펜타코론
옴니트런드 4단백질
대프리스마토데카초론 (Acronim: gippid) (Jonathan Bowers)
힌튼 폴리토프(콕시터)

이미지들

맞춤법 투사
A을_k 콕시터 평면	A을₄	A을₃	A을₂
그래프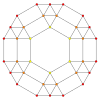
치측 대칭	[[5]] = [10]	[4]	[[3]] = [6]

그물
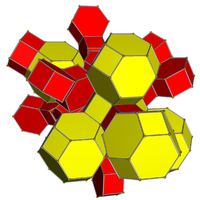옴니트런드 5세포	듀얼 - 옴니트런 5-셀

투시 투영


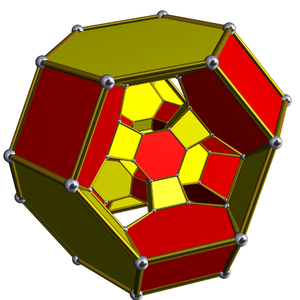투시 슐레겔 도표 잘린 팔면 중심	입체 투영법

순면체

잘린 옥타헤드론이 순서 4의 순면체인 것처럼, 잡동사니 5셀은 순서 5의 순면체다.^[2]잡동사니 5셀은 조노토프(zonotope)로, 5셀의 원점과 정점 5개를 통과하는 5줄에 평행한 5줄 세그먼트의 민코프스키 합이다.

직교 투영법(permutional as permutron

테셀레이션스

5개 셀의 벌집모양은 이 셀의 번역본으로 4차원 공간을 테셀링할 수 있으며, 각각 얼굴 주변에 3개의 하이퍼셀을 가지고 있다.이 벌집의 Coxeter 도표는.^[3] 3차원의 아날로그 벌집과 달리, 3개의 서로 다른 Coxeter 그룹 Wythoff 시공을 가진 bitrunculated 큐빅 벌집과는 달리, 이 벌집에는 단 하나의 구조만이 있다.^[1]

대칭

모든 것이 다 된 5세포는 확장된 오타크 대칭인 [3,3,3], 순서 240을 가지고 있다.잡종 5세포의 정점 수치는 [3,3] 콕시터 그룹의 구르사트 사면체를 나타낸다.확장된 대칭은 중간 순서-3 분기에 걸쳐 2배 회전하며, [2⁺[3,3,3]]로 더 명확하게 표현된다.

좌표

에지 길이 2를 갖는 원점 중심의 전지형 5-셀의 정점에 대한 데카르트 좌표는 다음과 같다.

$\left(\pm {\sqrt {10},\pm {6},\pm {3},\pm 1\오른쪽)$ $\left(\pm {\sqrt {10},\pm {6},\0,\pm 2\오른쪽)$ $\pm \pm {\sqrt {10},\\sqrt {2}{3}},\\frac {5}{\sqrt {3},\pm 1\오른쪽)$ $\pm \pm {\sqrt {10},\\sqrt {2}{3}},\\frac {-1}{\sqrt {3},\pm 3\오른쪽)$ $\pm \pm {\sqrt {10},\\sqrt {2}{3},\\frac {-4}{3},\pm 2\오른쪽)$ $\left\sqrt {5}{2},\3\sqrt {3}{3}},\pm {3},\pm 1\오른쪽)$ $\left}{\sqrt{5}{2}},\3}\\sqrt {\frac {3}{3}}}\pm {3},\pm 1\오른쪽)$ $\left\sqrt {5}{2},\ 3{\sqrt {\frac {3}{3}}}}\0,\\\pm 2\오른쪽)$ $\left(-{\sqrt{5}{2}},\3}\\sqrt {\frac {3}{3}}}\0,\\pm 2\오른쪽)$	$\pm \left\sqrt{5}{2}}:\\frac {1}{1}{\sqrt{6}}}\\\frac {7}{\sqrt {3}},\pm 1\오른쪽)}$ $\pm \left\sqrt{5}{2}}:\\frac {1}{1}{\sqrt{6}}}\\\frac {-2}{\sqrt {3}},\pm 4\right)$ $\pm \left\sqrt {\frac {5}{2}}:\frac {1}{\sqrt {6}},\frac {-5}{\sqrt {3},\pm 3\오른쪽)$ $\pm \left\sqrt {5}{2}},\\\sqrt {3}{2}},\pm 2\오른쪽)$ $\pm \left\sqrt {5}{2}},\\\sqrt {3}{3}}}\\pm 4\right)$ $\pm \left\sqrt{5}{2}}:\\frac {-7}{\sqrt{6}}},\frac {5}{\sqrt {3}},\pm 1\오른쪽)$ $\pm \left\sqrt{5}{2}}:\\frac {-7}{\sqrt{6}}},\frac {-1}{\sqrt{3}},\pm 3\오른쪽)$	$\pm \left\sqrt{5}{2}}:\\frac {-7}{\sqrt {6}},\frac {-4}{\sqrt {3},\pm 2\오른쪽)$ $\pm \left(0,\ 4{\sqrt {2}{3}}},\\pm 1\오른쪽)$ $\pm \left(0,\ 4{\sqrt {2}{3}}},\\pm 3\오른쪽)$ $\pm \left(0,\ 4{\sqrt {2}{3}}}\\frac {-4}{\sqrt {3}},\pm 2\오른쪽)$ $\pm \left(0,\ 2{\sqrt {2}{3}}},\\pm 1\오른쪽)$ $\pm \left(0,\ 2{\sqrt {2}{3}}},\pm 4\오른쪽)$ $\pm \left(0,\ 2{\sqrt {2}{3}},\\frac {-5}{\sqrt {3},\pm 3\오른쪽)$

이러한 정점은 (0,1,2,3,4)의 120 순열로 5-공간에서 더 단순하게 얻을 수 있다.이 구조는 5개의 직교, t_0,1,2,3{3,3,3,4}, .

풀 스너브 5셀

옴니스너브 5-셀의 꼭지점

옴니즈너브 5셀 또는 옴니즈너브 5셀의 전체 스너브 5셀은 균일하게 만들 수 없지만, Coxeter 도표 와 대칭 [3,3],⁺ 순서 120, 90셀: 이코사헤드론 10개, 팔면 20개, 정점 60개: 정점 삭제된 정점에서의 간격을 채우는 사면체 60개로 구성될 수 있다.얼굴 300면(삼각형), 가장자리 270면, 꼭지점 60면이다.

토폴로지로는 가장 높은 대칭인 [3,3]⁺ 아래에 10개의 이코사헤드라는 T(치랄 사면체) 대칭을 가지고 있는 반면, 20개의 옥타헤드라는₃ D 대칭을 가지고 있고 60개의 사면체는₂ C 대칭을 가지고 있다.^[4]

메모들

^ ^a ^b 기하학의 아름다움: 12편의 에세이(1999년), 도버 출판사, LCCN99-35678, ISBN0-486-40919-8 (조노헤드라의 분류, 73페이지)
^ 순서 5의 순면체
^ 조지 올셰프스키, 균일한 파노플로이드 테트라콤브스, 원고(2006):테셀레이션을 [140/143] 대프리스마토다코리아 테트라콤(Omnitruncaled pentachoric 4d honeycomb)으로 나열한다.
^ "S3s3s3s".

참조

H.S.M. Coxeter:
- H.S.M. Coxeter, 일반 폴리토페스, 제3판 도버 뉴욕, 1973년
- 케일리디스코어: H.S.M. Coxeter의 선별된 글, F가 편집한 글.아서 셔크, 피터 맥멀런, 앤서니 C.Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  - (용지 22) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 I, [산술]Zeit. 46 (1940) 380-407, MR 2,10]
  - (용지 23) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 II, [수학]Zeit. 188 (1985) 559-591]
  - (용지 24) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 III, [산술]Zeit. 200 (1988) 3-45]
Norman JohnsonUniform Polytopes, 원고(1991)
- N.W. 존슨:균일다각체와 허니컴의 이론, 박사학위.
1. 펜타코론 – 모델 5, 8, 9, 조지 올셰프스키에 바탕을 둔 볼록한 균일 폴리초라.
Klitzing, Richard. "4D uniform polytopes (polychora)". o3x3x3o - spid, x3x3o3x - prip, x3x3x3x - gippid

v t 치수 2-10의 기본 볼록형 일반 및 균일한 폴리토프
가족	A_n	B_n	I₂(p) / D_n	E₆ / E₇ / E₈ / F₄ / G₂	H_n
정규 다각형	삼각형	사각형	p-곤	육각형	펜타곤
균일다면체	사면체	옥타헤드론 • 큐브	데미큐브		도데카헤드론 • 이코사헤드론
균일 폴리초론	펜타코론	16-셀 • 테세락트	데미테세락트	24셀	120 셀 • 600 셀
제복5폴리토프	5와섹스	5정형 • 5정형	5데미큐브
제복6폴리토프	6-630x	6-정통 • 6-118	6데미큐브	1₂₂ • 2₂₁
제복7폴리토프	7시 15분	7정맥 • 7정맥	7데미큐브	1₃₂ • 2₃₁ • 3₂₁
제복8폴리토프	8시 15분	8정형 • 8정형	8데미큐브	1₄₂ • 2₄₁ • 4₂₁
제복9폴리토프	9시 15분	9-정통 • 9-11	9데미큐브
균일 10폴리토프	10센트짜리	10정형 • 10정형	10데미큐브
균일 n폴리토프	n-제곱스	n-직관 • n-직관	n-데미큐브	1_k2 • 2_k1 • k₂₁	n-자갈 폴리토프
주제: 폴리토페 패밀리 • 일반 폴리토페 • 일반 폴리토페 및 화합물 목록

[cox-1] 기하학의 아름다움: 12편의 에세이(1999년), 도버 출판사, LCCN99-35678, ISBN0-486-40919-8 (조노헤드라의 분류, 73페이지)

[2] 순서 5의 순면체

[3] 조지 올셰프스키, 균일한 파노플로이드 테트라콤브스, 원고(2006):테셀레이션을 [140/143] 대프리스마토다코리아 테트라콤(Omnitruncaled pentachoric 4d honeycomb)으로 나열한다.

[4] "S3s3s3s".

[1]

[2]

[3]

[4]

이름	5세포	잘린 5세포	교정된 5세포	알 수 있는 5세포	박리된 5세포	캔트런으로 된 5셀	윤이 나는 5세포	구획 5셀	잡동사니 5세포
슐레플리 심볼	{3,3,3} 3r{3,3}	t{3,3,3} 2t{3,3}	r{3,3,3} 2r{3,3}	rr{3,3} r2r{3,3}	2t{3,3}	tr{3,3} t2r{3,3}	t_0,3{3,3,3}	t_0,1,3{3,3,3} t_0,2,3{3,3,3}	t_0,1,2,3{3,3,3}
콕시터 도표를 만들다
슐레겔 도표를 만들다
A을₄ 콕시터 평면 그래프
콕시터 평면₃ 그래프
콕시터 평면₂ 그래프

Search

런케이티드 5-셀

네임스페이스

더

목차

런케이티드 5-셀

대체 이름

구조

해부

이미지들

좌표

루트 벡터

횡단면

투영

관련 꼬치 다면체

런시트드 5셀

대체 이름

이미지들

좌표

옴니트런드 5세포

대체 이름

이미지들

투시 투영

순면체

테셀레이션스

대칭

좌표

관련 폴리토페스

풀 스너브 5셀

관련 폴리토페스

메모들

참조