잘린 5 셀
Truncated 5-cell 5셀 |  잘린 5 셀 |  비트런치된5 셀 | |
| [3,3]을 중심으로 한 슐레겔 다이어그램([3,3]의 반대쪽 셀) | |||
기하학에서 잘린 5셀은 정규 5셀의 절단으로 형성된 균일한 4폴리토프(4차원 균일한 폴리토프)이다.
비트 트랜케이션을 포함한 2개의 트랜케이션이 있습니다.
잘린 5 셀
| 잘린 5 셀 | ||
|---|---|---|
 슐레겔도 (4면체 셀이 표시됨) | ||
| 유형 | 균일한 4-폴리토프 | |
| 슐레플리 기호 | t0,1{3,3,3} t{3,3,3} | |
| 콕서터 다이어그램 | ||
| 셀 | 10 | 5(3.3.3) 5(3.6.6) |
| 얼굴 | 30 | 20 {3} 10 {6} |
| 가장자리 | 40 | |
| 꼭지점 | 20 | |
| 꼭지점 도형 |  정삼각형 피라미드 | |
| 대칭군 | A4, [3,3] 주문 120 | |
| 특성. | 볼록, 등교 | |
| 균일한 지수 | 2 3 4 | |
잘린 5셀, 잘린 펜타코론 또는 잘린 4-단순은 10셀로 둘러싸여 있다: 5개의 사면체 및 5개의 사면체.각 정점은 3개의 잘린 사면체와 1개의 사면체로 둘러싸여 있다. 정점 도형은 긴 사면체이다.
건설
잘린 5 셀은 가장자리 길이의 1/3에서 정점을 잘라냄으로써 5 셀에서 구성할 수 있습니다.이것은 5개의 사면체 셀을 잘린 사면체로 변환하고, 원래의 꼭지점 근처에 위치한 5개의 새로운 사면체 셀을 도입합니다.
구조.
잘린 사각형은 육각형 면에서는 서로 결합되고, 삼각형 면에서는 사각형 면과 결합됩니다.
구성 매트릭스에서 볼 수 있듯이 요소 간의 모든 발생 카운트가 표시됩니다.대각선 f-벡터 번호는 Wythoff 구성을 통해 파생되며, [1]한 번에 하나의 미러를 제거하여 하위 그룹 순서의 전체 그룹 순서를 나눕니다.
| A4. | K면 | 에프k | 에프0 | 에프1 | 에프2 | 에프3 | k자릿수 | 메모들 | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A2. | ( ) | 에프0 | 20 | 1 | 3 | 3 | 3 | 3 | 1 | {3}v( ) | A4/A2 = 5!/3!= 20 | |
| A2A1 | { } | 에프1 | 2 | 10 | * | 3 | 0 | 3 | 0 | {3} | A4/AA21 = 5!/3!/2 = 10 | |
| A1A1 | 2 | * | 30 | 1 | 2 | 2 | 1 | { }v( ) | A4/AA11 = 5!/2/2 = 30 | |||
| A2A1 | t{3} | 에프2 | 6 | 3 | 3 | 10 | * | 2 | 0 | { } | A4/AA21 = 5!/3!/2 = 10 | |
| A2. | {3} | 3 | 0 | 3 | * | 20 | 1 | 1 | A4/A2 = 5!/3!= 20 | |||
| A3. | t{3,3} | 에프3 | 12 | 6 | 12 | 4 | 4 | 5 | * | ( ) | A4/A3 = 5!/4! = 5 | |
| {3,3} | 4 | 0 | 6 | 0 | 4 | * | 5 | |||||
투영
잘린 5셀의 3차원 공간에 대한 잘린 사면체-첫 번째 슐레겔 다이어그램 투영법은 다음과 같은 구조를 가진다.
- 투영 엔벨로프는 잘린 사면체입니다.
- 잘린 사면체 셀 중 하나가 전체 외피 위에 투영됩니다.
- 사면체 셀 중 하나는 포락선 중앙에 놓여 있는 사면체 위에 투영된다.
- 4개의 평탄한 사면체가 외피의 삼각면에 접합되어 4개의 방사형 가장자리를 통해 중앙 사면체와 연결된다.이것들은 나머지 4개의 사면체 세포들의 이미지입니다.
- 중앙 사면체와 엔벨로프의 4개의 육각면 사이에는 4개의 불규칙한 절단 사면체 부피가 있으며, 이는 나머지 4개의 절단 사면체 셀의 화상이다.
투영된 셀의 이러한 레이아웃은 잘린 4면체를 2차원 공간에 면 먼저 투영하는 면 레이아웃과 유사합니다.잘린 5셀은 잘린 사면체의 4차원 유사체이다.
이미지들
| Ak. 콕서터 평면 | A4. | A3. | A2. |
|---|---|---|---|
| 그래프 | 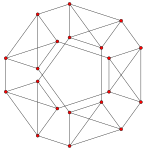 |  | 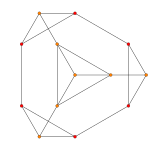 |
| 이면체 대칭 | [5] | [4] | [3] |
대체 이름
- 잘린 펜타토프
- 잘린 4-심플렉스
- 잘린 펜타코론(Acronym: 팁)(Jonathan Bowers)
좌표
가장자리 길이 2를 갖는 원점 중심 잘린 5 셀의 정점에 대한 데카르트 좌표는 다음과 같다.
| | |
보다 간단하게 말하면, 잘린 5 셀의 정점은 (0,0,0,1,2) 또는 (0,1,2,2)의 순열로서 5 공간내의 하이퍼 플레인상에 구성될 수 있다.이러한 좌표는 각각 잘린 펜타크로스와 비트런치 펜터팩트의 양의 직교면에서 나온다.
관련 폴리토프
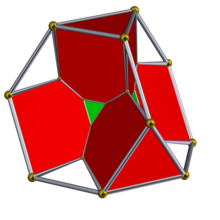
잘린 5개의 세포와 그 이중의 볼록한 껍질은 60개의 세포로 구성되어 있다: 10개의 사면체, 20개의 팔면체, 30개의 사면체, 40개의 꼭지점.그것의 꼭지점 모양은 육각 삼각형 큐폴라이다.
비트런치된5 셀
| 비트런치된5 셀 | ||
|---|---|---|
 대체 셀이 숨겨져 있는 슐레겔 다이어그램. | ||
| 유형 | 균일한 4-폴리토프 | |
| 슐레플리 기호 | t1,2{3,3,3} 2t{3,3,3} | |
| 콕서터 다이어그램 | 또는 | |
| 셀 | 10(3.6.6) | |
| 얼굴 | 40 | 20 {3} 20 {6} |
| 가장자리 | 60 | |
| 꼭지점 | 30 | |
| 꼭지점 도형 | 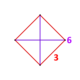 ({ }v{ }) | |
| 이중 폴리토프 | 분리 30셀 | |
| 대칭군 | Aut(A4), [[3,3,3]], 주문 240 | |
| 특성. | 볼록, 등각, 등각, 등각 | |
| 균일한 지수 | 567 | |
비트런치된 5세포(비트런치된 펜타코론, 데카코론 및 10세포라고도 함)는 잘린 사면체 모양의 10개의 세포로 구성된 4차원 폴리토프 또는 4-폴리토프입니다.
위상학적으로 가장 높은 대칭인 [[3,3,3]] 아래에는 10개의 균일한 잘린 사면체를 포함하는 하나의 기하학적 형태가 있다.6각형은 폴리코론의 반전 대칭 때문에 항상 규칙적이며, 디트리곤 중 유일하게 규칙적인 경우(3배 대칭을 가진 등각 육각형)이다.
E. L. Elte는 1912년에 그것을 반규칙 폴리포프라고 확인했다.
절삭사면체의 각 육각면은 인접한 절삭사면체에 상호보완방향으로 접합되어 있다.각 모서리는 두 개의 육각형과 하나의 삼각형으로 공유됩니다.각 정점은 사각형 디셰노이드 정점 도형에서 4개의 잘린 사면체 셀로 둘러싸여 있다.
비트런치된5 셀은 듀얼 구성의 2개의 펜타코라의 교차점입니다.이와 같이, 펜터팩트의 긴 대각선을 직교로 양분하는 것은 펜터팩트와 하이퍼플레인의 교차점이기도 합니다.이 점에서 정팔면체(이중 구성의 정사면체/긴 대각선의 정사면체/정사면체 이등분)와 정육각형(정삼각형/입방체)의 4차원 유사체이다.5차원 아날로그는 2방향화된 5-단순화이며, n ndimensional 아날로그는 콕서터-Dynkin 다이어그램이 중간 하나 또는 두 개의 노드에 고리가 있는 선형인 폴리토프이다.
비트런치된 5셀은 셀 전이성이 있는 2개의 불규칙 균일한4 폴리토프 중 하나입니다.다른 하나는 48개의 잘린 큐브로 구성된 비트런치된 24 셀입니다.
대칭
이 4-폴리토프는 더 높은 확장 펜타코리 대칭(2×A4, [[3,3,3])을 가지며, 2배인 240을 가진다. 왜냐하면 기초가 되는 5 셀의 어떤 원소에 대응하는 원소는 이중의 원소에 대응하는 원소 중 하나와 교환될 수 있기 때문이다.
대체 이름
- 비트런치된 5셀(Norman W. Johnson)
- 세포 전이성 4-폴리토프로서의 10세포
- 비트런컷 펜타코론
- 비트런컷 펜타토프
- 비트런컷된 4-심플렉스
- 데카초론(Acronym: deca)(Jonathan Bowers)
이미지들
| Ak. 콕서터 평면 | A4. | A3. | A2. |
|---|---|---|---|
| 그래프 |  |  |  |
| 이면체 대칭 | [[5]] = [10] | [4] | [[3]] = [6] |
 구면 4 폴리토프의 입체 투영 (육각형 면을 중심으로) |  네트(폴리토프) |
좌표
에지 길이 2를 가진 원점 중심 비트런치 5 셀의 데카르트 좌표는 다음과 같습니다.
| 좌표 | |
|---|---|
| | |
보다 간단하게 비트런으로 분할된 5셀의 정점은 (0,0,1,2,2)의 순열로 5공간 하이퍼플레인 상에 구성될 수 있다.이것들은 비트런컷된 펜타크로스의 양의 직교면을 나타냅니다.원점을 중심으로 하는 또 다른 5공간 구성은 모두 (-1,-1,0,1,1)의 20개 순열입니다.
관련 폴리토프
비트런치된5 셀은 2개의 표준5 셀이 듀얼 위치에 있는 교차점으로 간주할 수 있습니다.![]()
![]()
![]() = 。
= 。
| 어둡다. | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| 이름. 콕서터 | 육각형 t{3} = {6} | 팔면체 r{3,3} = {31,1} = {3,4} | 데카초론 2t{33} | 도데카테론 2r{34} = {32,2} | 테트라데카페톤 3t{35} | 헥사데옥손 3r{36} = {33,3} | 옥타데카제톤 4t{37} |
| 이미지들 |  |   |   |   |   |   |   |
| 꼭지점 도형 | ( )v( ) |  { }×{ } |  { }v { } |  {3}×{3} |  {3}v{3} | {3,3}x{3,3} |  {3,3}v{3,3} |
| 면 | {3} | t{3,3} | r{3,3,3} | 2t{3,3,3,3} | 2r{3,3,3,3} | 3t{3,3,3,3,3,3} | |
| ~하듯이 교차하고 있다 이중의 심플렉스 |  |  |   |
관련 규칙 스큐 다면체
정사각형 스큐 다면체 {6,4 3}은 지그재그 비평면 정점 도형으로 각 정점을 중심으로 4개의 육각형으로 4개의 공간에 존재합니다.이러한 육각형 면은 60개의 모서리와 30개의 정점을 모두 사용하여 비트런치된 5셀에서 볼 수 있습니다.비트런치된 5셀의 20개의 삼각형 면은 제거된 것으로 볼 수 있습니다.이중 규칙 스큐 다면체 {4,6 3)은 런케이트된 5 셀의 정사각형 면과 유사하게 관련되어 있습니다.
분리 30셀
| 분리 30셀 | ||
|---|---|---|
| 유형 | 완전[2] 폴리코론 | |
| 기호. | f1,2A4[2] | |
| 콕서터 | ||
| 셀 | 30개의 일치된 정사각형 디스포이드 | |
| 얼굴 | 60개의 이등분 (짧은 가장자리 2개) | |
| 가장자리 | 40 | 1의 20 \ 1 3의 20(\criptstyle\ |
| 꼭지점 | 10 | |
| 꼭지점 도형 |  (트리아키스 사면체 | |
| 듀얼 | 비트런치된5 셀 | |
| 콕서터군 | Aut(A4), [[3,3,3]], 주문 240 | |
| 궤도 벡터 | (1, 2, 1, 1) | |
| 특성. | 볼록, 등화성 | |
분리형 30셀은 비트런치된 5셀의 듀얼입니다.5셀에서 파생된 4차원 폴리토프(또는 폴리코론)입니다.반대 방향의 2개의 5셀의 볼록한 선체입니다.
균일한 폴리코론의 쌍대이기 때문에 세포 전이성이며 30개의 합동 4각형 디셰노이드로 구성됩니다.또한 Aut(A4)군에서는 정점 전이적이다.
관련 폴리토프
이 폴리토프는 [3,3,3] 콕서터기로 구성된 9개의 균일한 4-폴리토프 집합에서 가져온 것이다.
| 이름. | 5셀 | 잘린 5셀 | 정류된 5셀 | 캔텔화 5셀 | 비트런치 5셀 | 절단된 5세포 | runcated 5셀 | runcitruncated 5세포 | 옴니트 절단된 |
|---|---|---|---|---|---|---|---|---|---|
| 슐레플리 기호. | {3,3,3} 3r{3,3,3} | t{3,3,3} 2t{3,3,3} | r{3,3,3} 2r{3,3,3} | rr{3,3,3} r2r{3,3,3} | 2t{3,3,3} | tr{3,3,3} t2r{3,3,3} | t0,3{3,3,3} | t0,1,3{3,3,3} t0,2,3{3,3,3} | t0,1,2,3{3,3,3} |
| 콕서터 도표 | |||||||||
| 슈레겔 도표 |  |  |  |  |  |  |  |  |  |
| A4. 콕서터 평면 그래프 |  |  |  |  |  |  |  |  |  |
| 콕서터 비행기3 그래프 |  |  |  |  |  |  |  |  |  |
| 콕서터 비행기2 그래프 |  |  |  |  |  |  |  |  |  |
레퍼런스
- H.S.M. 콕서터:
- H.S.M. Coxeter, Regular Polytopes, 제3판, 도버 뉴욕, 1973년
- 만화경: H.S.M. 콕서터 선정필, F. 편집자 F.S.M. 콕서터.아서 셔크, 피터 맥멀런, 앤서니 CThompson, Asia Ivic Weiss, Wiley-Intercience Publication, 1995, ISBN978-0-471-01003-6[1]
- (페이퍼 22) H.S.M. 콕서터, 정규 및 준정규 폴리토피스 I, [수학]Zeit.46 (1940) 380-407, MR 2,10]
- (페이퍼 23) H.S.M. 콕서터, 정규 및 반정규 폴리토피스 II, [수학]Zeit. 188 (1985) 559-591]
- (문서 24) H.S.M. 콕서터, 정규 및 반정규 폴리토피스 III, [수학]Zeit. 200 (1988) 3-45]
- 콕서터, 기하학의 아름다움: 12 에세이, 도버 출판물, 1999, ISBN0-486-40919-8 페이지 88 (5장: 3차원 및 4차원의 정규 스큐 다면체와 그 위상유사, 런던 수학회 회보, Ser. 2, Vol 43, 1937).
- 콕서터, H.S.M. 3차원 및 4차원의 정규 스큐 다면체검사, 런던 수학.43호, 33-62, 1937년
- Norman Johnson Uniform Polytopes, 원고(1991)
- N.W. 존슨:균일한 폴리토프와 허니콤 이론 박사(1966년)
- 1. 펜타코론에 기초한 볼록 균일한 폴리코라 - 모델 3, 조지 올셰프스키.
- Klitzing, Richard. "4D uniform polytopes (polychora)". x3x3o - 팁, o3x3o - 데카
- 특정한
- ^ Klitzing, Richard. "x3x4o3o - tip".
- ^ a b 완벽한 4-폴리토프 Gabor Gévay의 대수 및 기하학에 대한 기여에 대하여 제43권 (2002년), No.1, 243-259] 표 2, 252페이지
| 가족 | An | Bn | I2(p) / Dn | E6/E7/E8/F4/G2 | Hn | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 정다각형 | 삼각형 | 광장 | p곤 | 육각형 | 펜타곤 | |||||||
| 균일한 다면체 | 사면체 | 8면체 • 큐브 | 데미큐브 | 12면체 • 이십면체 | ||||||||
| 균일한 폴리코론 | 펜타코론 | 16 셀 • 테서랙트 | 데모테서랙트 | 24 셀 | 120 셀 • 600 셀 | |||||||
| 균일한 5 폴리토프 | 51200x | 5 - ORTOPLEX • 5 - 큐브 | 5 데미큐브 | |||||||||
| 균일한 6 폴리토프 | 61200x | 6-정류 • 6-큐브 | 6-데미큐브 | 122 • 221 | ||||||||
| 균일한 7 폴리토프 | 71200x | 7-정류 • 7-큐브 | 7 데미큐브 | 132 • 231 • 321 | ||||||||
| 균일한 8 폴리토프 | 8180x | 8-정류 • 8-큐브 | 8개의 데미큐브 | 142 • 241 • 421 | ||||||||
| 균일한 9-폴리토프 | 9169x | 9-정류 • 9-입방체 | 9데미큐브 | |||||||||
| 균일한 10 폴리토프 | 10-1996x | 10 - ORTOPLEX • 10 - 큐브 | 10 데미큐브 | |||||||||
| 균일한 n-폴리토프 | n-1996x | n-ortoplex • n-입방체 | n-데미큐브 | 1k2 • 2k1 • k21 | n-오각형 폴리토프 | |||||||
| 주제: 폴리토프 패밀리 • 일반 폴리토프 • 일반 폴리토프 및 화합물 목록 | ||||||||||||