스칼라 전위
Scalar potential수학물리학에서 스칼라 전위는 간단히 말해서 두 개의 다른 위치에서 물체의 전위 에너지 차이가 한 위치에서 다른 위치로 이동할 때 물체가 취하는 경로가 아니라 위치에만 의존하는 상황을 설명한다. 위치에만 의존하는 방향 없는 값(scalar)인 3공간의 스칼라장이다. 익숙한 예는 중력에 의한 전위 에너지다.
스칼라 전위는 벡터 분석과 물리학의 기본 개념이다(벡터 전위와 혼동의 위험이 없다면 형용사 스칼라는 자주 생략된다). 스칼라 전위는 스칼라장의 예다. 벡터 필드 F에 따라 스칼라 전위 P는 다음과 같이 정의된다.
여기서 ∇P는 P의 구배이며, 방정식의 두 번째 부분은 데카르트 좌표 x, y, z 함수의 구배에서 구배를 뺀 것이다.[2] 어떤 경우에 수학자들은 잠재력을 정의하기 위해 구배 앞에 있는 긍정적인 기호를 사용할 수 있다.[3] 구배 측면에서 P의 이러한 정의 때문에, 어느 지점에서 F의 방향은 그 지점에서 P의 가장 가파른 감소 방향이며, 그 크기는 단위 길이당 그 감소율이다.
F가 스칼라 전위적인 면에서만 설명되려면, 다음과 같은 동등한 문장이 모두 참이어야 한다.
- , where the integration is over a Jordan arc passing from location a to location b and P(b) is P evaluated at location b .
- = 여기서 적분은 Jordan 곡선이라고도 하는 단순한 폐쇄 경로 위에 있다.
이러한 조건 중 첫 번째는 그라데이션의 기본 정리를 나타내며, 서로 다른 가치의 단일 스칼라 필드 P의 구배인 벡터 필드에 대해 참이다. 두 번째 조건은 스칼라 함수의 경사로 표현될 수 있도록 F의 요건이다. 세 번째 조건은 컬의 기본 정리를 이용하여 F의 컬이라는 관점에서 두 번째 조건을 다시 표현한다. 이러한 조건을 만족시키는 벡터장 F는 비회전적(보수적)이라고 한다.
스칼라 잠재력은 물리학과 공학에서 많은 분야에서 두드러진 역할을 한다. 중력 전위는 위치 함수로서 단위 질량 당 중력과 관련된 스칼라 전위, 즉 장으로 인한 가속도이다. 중력 전위는 단위 질량 당 중력 전위 에너지다. 전기 공학에서 전위는 전기장과 관련된 스칼라 전위(즉, 단위 전하당 정전력)이다. 이 경우 전위는 단위 전하당 정전기 전위 에너지다. 유체 역학에서 비회전성 성층장은 라플라시안 필드일 때만 특별한 경우에 한하여 스칼라 전위를 가진다. 핵무기의 특정 측면은 유카와 전위적으로 설명할 수 있다. 그 잠재력은 고전 역학의 라그랑기안과 해밀턴식 형식에서 두드러진 역할을 한다. 더욱이 스칼라 전위는 양자역학의 근본적인 양이다.
모든 벡터장이 스칼라 전위를 가지는 것은 아니다. 그런 것들을 보수주의라고 부르는데, 이는 물리학에서 보수적인 힘의 개념에 해당된다. 비보수 세력의 예로는 마찰력, 자기력, 유체역학에서는 솔레노이드장 속도장이 있다. 그러나 헬름홀츠 분해 정리에 의해 모든 벡터 장은 스칼라 전위 및 해당 벡터 전위 측면에서 설명할 수 있다. 전기역학에서 전자기 스칼라와 벡터 전위는 전자기 4전위라고 함께 알려져 있다.
통합성 조건
F가 보수적인 벡터 필드(비회전, 컬프리 또는 잠재력이라고도 함)이고 그 구성요소가 연속적인 부분파생상품을 갖는 경우 기준점 0 {에 대한 F의 잠재력은 선 적분 측면에서 정의된다.
여기서 C는 에서 r{\까지의 매개 변수화된 경로다.
선 적분선이 그 단자점 및 {\을 통해서만 경로 C에 의존한다는 사실은 본질적으로 보수적인 벡터 필드의 경로 독립성 속성이다. 라인 통합의 기본 정리는 V가 방식으로 정의되면 = - V, 을(를) 의미하므로 V는 보수적인 벡터 필드 F의 스칼라 잠재력이 된다. 스칼라 전위는 벡터장만으로 결정되는 것이 아니다. 실제로 함수의 구배는 상수를 추가하면 영향을 받지 않는다. V가 라인 적분으로 정의되어 있는 경우, V의 모호성은 기준점 r 의 선택에 있어 자유를 반영한다.
중력 전위 에너지로서의 고도

예를 들면 지구 표면 근처에 있는 균일한 중력장이 있다. 그것은 잠재적인 에너지를 가지고 있다.
여기서 U는 중력 전위 에너지, h는 표면 위의 높이다. 이것은 등고선도의 중력 전위 에너지가 고도에 비례한다는 것을 의미한다. 등고선도에서 고도의 2차원 음경사는 2차원 벡터장으로 벡터는 항상 등고선에 수직이며 또한 중력 방향에도 수직이다. 그러나 등고선도로 대표되는 구릉지대에서 U의 3차원 음의 구배는 항상 중력 방향으로 곧장 아래를 향한다; F. 그러나 언덕을 굴러 내려가는 공은 언덕 표면의 정상적인 힘 때문에 언덕의 표면에 수직으로 작용하는 중력 성분을 상쇄시키는 직접적인 하방으로 움직일 수 없다. 볼을 이동하기 위해 남아 있는 중력의 구성 요소는 표면과 평행하다.
여기서 θ은 경사각이며, F의S 구성요소는 중력에 수직이다.
지면에 평행한P 이 힘 F는 θ이 45도일 때 가장 크다.
Δh를 등고선 지도에서 등고선 사이의 고도의 균일한 구간으로 하고 Δx를 두 등고선 사이의 거리로 한다. 그러면
하도록
그러나 등고선도에서 구배는 Δx에 반비례하여 등고선도의 FP: 고도가 정확히 2차원 전위장은 아니다. 힘의 크기는 다르지만, 힘의 방향은 등고선도와 등고선도로 대표되는 지구 표면의 구릉지대에서 동일하다.
부력 전위로서의 압력
유체역학에서는 평형을 유지하지만 균일한 중력장이 존재하는 곳에서는 중력을 상쇄하는 균일한 부력력에 의해 유체가 스며든다: 그것이 유체가 평형을 유지하는 방법이다. 이 부력력은 압력의 음의 구배다.
부력력은 중력의 반대 방향으로 위쪽을 가리키기 때문에 유체의 압력이 아래쪽으로 증가한다. 정적인 물체의 압력은 수면 아래의 깊이에 비례하여 증가한다. 일정한 압력의 표면은 표면에 평행한 평면으로, 0압력의 평면으로 특징지을 수 있다.
액체가 수직 소용돌이(회전 축이 표면에 수직인 경우), 그 소용돌이는 압력장에 우울증을 일으킨다. 볼텍스 내부의 액체 표면은 동일한 압력의 어떤 표면과 마찬가지로 아래로 당겨지며, 액체 표면과 평행하게 유지된다. 효과는 소용돌이 내부에서 가장 강하며 소용돌이 축과의 거리에 따라 빠르게 감소한다.
고체 물체에 담그고 그 액체로 둘러싸인 유체에 기인한 부력력은 물체 표면을 따라 음압 기울기를 통합하여 얻을 수 있다.
유클리드 공간의 스칼라 전위
3차원 유클리드 공간 에서 비회전 벡터 필드 E의 스칼라 전위는 다음에 의해 주어진다.
여기서 ) 은 r'에 대한 최소 볼륨 요소다. 그러면
이 홀드는 E가 연속적이고 무증상적으로 무한을 향해 0으로 사라지며 1/r보다 빠르게 붕괴되고 E의 분산이 마찬가지로 무한을 향해 사라지면 1/r보다2 빠르게 붕괴한다.
다른 방법으로 쓰자.
뉴턴의 잠재력이다 이것은 Ⅱ의 라플라시안이 디락 델타 함수의 음과 같다는 뜻의 라플라스 방정식의 근본 해법이다.
그 다음 스칼라 전위는 γ과 E의 경련(convolution)의 분화다.
실제로 회전 불변 잠재력을 가진 비회전 벡터장의 콘볼루션도 비회전적이다. 비회전 벡터 필드 G의 경우 다음과 같이 나타낼 수 있다.
그러므로
필요에 따라
더 일반적으로, 공식은
n차원 유클리드 공간(n > 2)에서 뉴턴의 전위가 주어지는 경우
여기서 Ω은n 단위 n-ball의 체적이다. 그 증거는 동일하다. 또는 부품별 통합(또는 보다 엄격하게, 콘볼루션의 특성)은 다음과 같다.
참고 항목
- 그라데이션 정리
- 벡터 분석의 기본 정리
- 등전위(등전위) 선 및 표면
참조
- ^ Herbert Goldstein. Classical Mechanics (2 ed.). pp. 3–4. ISBN 978-0-201-02918-5.
- ^ 이 방정식의 두 번째 부분은 데카르트 좌표에만 유효하며, 원통형 좌표나 구형 좌표와 같은 다른 좌표계는 구배도의 기본 정리에서 파생된 더 복잡한 표현을 하게 될 것이다.
- ^ 음극 없이 전위가 정의된 예는 [1]을 참조하십시오. 함수의 구배에서 함수에 대해 해결할 때 전위라는 용어를 사용하지 않는 것과 같은 기타 참조.





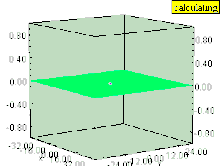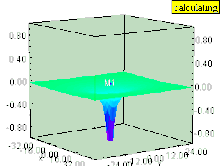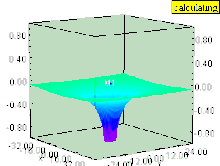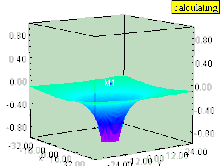




 (를) 의미하므로 V는 보수적인 벡터 필드 F의 스칼라 잠재력이 된다. 스칼라 전위는 벡터장만으로 결정되는 것이 아니다. 실제로 함수의 구배는 상수를 추가하면 영향을 받지 않는다. V가 라인 적분으로 정의되어 있는 경우, V의 모호성은 기준점 r
(를) 의미하므로 V는 보수적인 벡터 필드 F의 스칼라 잠재력이 된다. 스칼라 전위는 벡터장만으로 결정되는 것이 아니다. 실제로 함수의 구배는 상수를 추가하면 영향을 받지 않는다. V가 라인 적분으로 정의되어 있는 경우, V의 모호성은 기준점 r