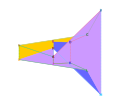
토로이드 다면체

Toroidal polyhedron
다면 토러스 표면은 이 6x4 예와 같이 4면 표면의 그물로부터 대략적으로 구성될 수 있다.

기하학에서 토로이드 다면체(toroidal polyheadron)는 다면체로서, 토폴로지 속은 1 이상이다. 주목할 만한 예로는 차사르와 실라시 다면체 등이 있다.

정의의 변화

Toroidal polyedra는 그들의 가장자리와 꼭지점에서 만나는 다각형의 집합으로 정의되며, 그것들 처럼 다지관을 형성한다. 즉, 각 가장자리는 정확히 두 개의 다각형에 의해 공유되어야 하며, 각 꼭지점의 링크는 그 정점에서 만나는 가장자리와 다각형을 번갈아 연결하는 단일 사이클이어야 한다. Toroidal polyedra의 경우, 이 다지관은 방향성이 있는 표면이다.[1] 일부 저자들은 "토로이드 다면체"라는 문구를 보다 구체적으로 다면체학적으로 (genus 1) 토루스(torus 1)와 동등한 의미를 가지도록 제한한다.[2]

이 영역에서는 자기 자신이나 서로 교차하지 않는 3차원 유클리드 공간에서 납작한 다각형인 내장형 토로이드 다면체와 특정한 기하학적 실현이 없는 추상적 다면체 표면을 구분하는 것이 중요하다.[3] 이 두 극단의 중간은 유클리드 공간의 기하학적 다각형이나 별 다각형에 의해 형성된 다면체다.

이 모든 경우에 다면체의 토로이드 성질은 그것의 방향성과 그것의 오일러 특성이 비양성으로 확인될 수 있다. 오일러 특성은 V - E + F = 2 - 2N으로 일반화되며 여기서 N은 구멍 수입니다.

체사르와 실라시 다면체

대화형 Csaszar 다면체 모델 – SVG 영상에서 마우스를 왼쪽과 오른쪽으로 이동하여 회전시키십시오.[4]
대화형 실라시 다면 모델 – SVG 영상에서 마우스를 움직여 회전시키십시오.[5]

가장 간단한 내장형 토로이드 다면체 중 두 가지는 Csaszarr와 Szilassi 다면체다.

까사사르 다면체는 가장자리가 21개, 삼각형이 14개인 7Verex toroidal polyhedron이다.[6] 그것과 사면체는 두 정점을 연결하는 모든 가능한 선 세그먼트가 다면체의 가장자리를 형성하는 알려진 유일한 다면체다.[7] 그것의 이중인 질라시 다면체는 모두 서로 인접해 있는 7개의 육각형 얼굴을 가지고 있기 때문에 (천재 1) 토루스 지도에 필요한 색의 최대 수가 7개라는 정리의 반을 제공한다.[8][9]

Csaszarr 다면체는 내장형 토로이드 다면체의 정점이 가장 적고, Szilassi 다면체는 내장형 토로이드 다면체의 가능한 얼굴이 가장 적다.

스튜어트 토로이드

특수 범주의 토로이드 다면체는 교차 없이 정규 다각형 면에 의해서만 구성되며, 인접 면은 서로 같은 면에 놓여 있지 않을 수 있다는 추가적인 제한으로 구성된다. 이를 집중적으로 연구한 보니 스튜어트의 이름을 따서 스튜어트 토로이드라고 한다.[10][11] 그것들은 볼록한 다면체의 경우 존슨 고형물과 유사하지만, 존슨 고형물과 달리 스튜어트 토로이드가 무한히 많다.[12] 그것들은 또한 얼굴들이 모두 등변 삼각형인 다면체인 toroidal deltahedra도 포함한다.

스튜어트가 정의한 스튜어트 토로이드의 제한된 계급은 준콘벡스 토로이드 다면체다. 이것들은 그들의 볼록한 선체의 모든 가장자리를 포함하는 스튜어트 토로이드 입니다. 그러한 다면체의 경우 볼록한 선체의 각 면은 토로이드 표면에 놓여 있거나, 또는 가장자리가 모두 토로이드 표면에 놓여 있는 다각형이다.[13]

단일 다면체의 증강에 의한 Stewart toroids
속 1 1
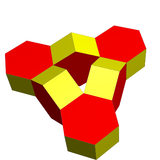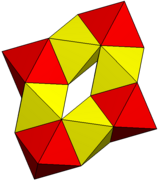이미지 Stewart toroid 6-hexprisms.png Eight octahedra toroid.png
폴리헤드라 육각 프리즘 6개 8옥타헤드라
정점 48 24
가장자리 84 72
얼굴 36 48
준콘벡스 스튜어트 토로이드
속 1 3 11 3 5 7 11
이미지 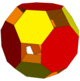Excavated truncated cube.png Excavated truncated octahedron1.png Excavated truncated octahedron2.png Excavated expanded cuboctahedron.png Excavated truncated cuboctahedron4.png Excavated truncated cuboctahedron2.png Excavated truncated cuboctahedron3.png Excavated truncated cuboctahedron.png
폴리헤드라 네모난 큐폴레
8 사면체 		6 삼각형 큐폴레 6개
6개의 사각 피라미드 		4삼각형 큐폴레
6개의 사각 피라미드 		24 삼각 프리즘
6개의 사각 피라미드
8 사면체 		6제곱 큐폴레
4삼각형 큐폴레
12 큐브 		삼각 큐폴레 8개
12 큐브 		6제곱 큐폴레
12 큐브 		6제곱 큐폴레
삼각 큐폴레 8개
볼록 선체 잘린 정육면체 잘린 팔면체 잘린 팔면체 팽창된 육면체 잘린 칸옥타헤드론 잘린 칸옥타헤드론 잘린 칸옥타헤드론 잘린 칸옥타헤드론
정점 32 30 30 62 72 72 72 72
가장자리 64 60 72 168 144 168 168 168
얼굴 32 30 38 86 68 88 84 76

자기 교차 다면체

Octahemioctahedron.png
옥타헤미오크타헤드론 		Small cubicuboctahedron.png
소형입방옥타헤드론 		Great dodecahedron.png
대두면체

폴리곤을 가로지르는 계통에 의해 형성된 다면체는 폴리곤과 그 계통의 공유된 가장자리 및 정점에 의해 형성된 추상 위상학적 다면체에 해당하며, 다면체의 속은 이 추상 다면체로부터 결정될 수 있다. 예를 들면, 1옥타헤미오엑타헤드론, 3옥타옥타헤드론, 4옥타헤드론 등이 있다.

왕관다면체

오각형 스테파노이드. 이 스테파노이드에는 오각 대칭이 있으며 균일한 오각형 프리즘과 정점이 같다.

왕관 다면체 또는 스테파노이드(Stephanoid)는 이소각(동일한 정점)과 등면(동일한 얼굴)이 모두 되어 고귀하기도 한 토로이드 다면체다. 왕관 다면체는 자기 분열적이고 위상적으로 자기 이중적이다.[14]

참고 항목

참조

  1. ^ 화이트리(1979년), 스튜어트(1980년), 페이지 15.
  2. ^ Webber, William T. (1997), "Monohedral idemvalent polyhedra that are toroids", Geometriae Dedicata, 67 (1): 31–44, doi:10.1023/A:1004997029852, MR 1468859, S2CID 117884274.
  3. ^ Whiteley, Walter (1979), "Realizability of polyhedra" (PDF), Structural Topology (1): 46–58, 73, MR 0621628.
  4. ^ 아코스 차사르, A Polyhedron Without Diagnals, Bolyai Institute, Szeed, 1949년
  5. ^ Grünbaum, Branko; Szilassi, Lajos (2009), "Geometric Realizations of Special Toroidal Complexes", Contributions to Discrete Mathematics, 4 (1): 21–39, doi:10.11575/cdm.v4i1.61986, ISSN 1715-0868
  6. ^ Császár, A. (1949), "A polyhedron without diagonals", Acta Sci. Math. Szeged, 13: 140–142.
  7. ^ Ziegler, Günter M. (2008), "Polyhedral Surfaces of High Genus", in Bobenko, A. I.; Schröder, P.; Sullivan, J. M.; Ziegler, G. M. (eds.), Discrete Differential Geometry, Oberwolfach Seminars, vol. 38, Springer-Verlag, pp. 191–213, arXiv:math.MG/0412093, doi:10.1007/978-3-7643-8621-4_10, ISBN 978-3-7643-8620-7, S2CID 15911143.
  8. ^ Szilassi, Lajos (1986), "Regular toroids" (PDF), Structural Topology, 13: 69–80[permanent dead link].
  9. ^ Heawood, P. J. (1890), "Map colouring theorems", Quarterly Journal of Mathematics, First Series, 24: 322–339
  10. ^ Webb, Robert (2000), "Stella: polyhedron navigator", Symmetry: Culture and Science, 11 (1–4): 231–268, MR 2001419.
  11. ^ Stewart, B. M. (1980), Adventures Among the Toroids: A Study of Orientable Polyhedra with Regular Faces (2nd ed.), B. M. Stewart, ISBN 978-0-686-11936-4.
  12. ^ 스튜어트(1980), 페이지 15.
  13. ^ 스튜어트(1980), "Quasi-conflexity and 약한 준 confectivity" 76–79페이지.
  14. ^ 특히Grünbaum, Branko (1994), "Polyhedra with Hollow Faces", Polytopes: Abstract, Convex and Computational, NATO ASI Series C: Mathematical and Physical Series, vol. 440, Kluwer Academic Publishers, pp. 43–70, doi:10.1007/978-94-011-0924-6_3 60쪽을 보라.

외부 링크