잘린 24셀 벌집

잘린 24셀 벌집
(이미지 없음)
유형	제복4벌집
슐레플리 기호	t{3,4,3,3} tr{3,3,4,3} t2r{4,3,4} t2r{4,3,31,1} t{31,1,1,1}
콕시터-딘킨 도표
4면형	테세락트 잘린 24셀
세포형	큐브 잘린 팔면체
얼굴형	사각형 삼각형
정점수	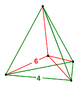사면 피라미드
콕시터 그룹	${\displaystyle {\stackrel{}{F}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$ [3,4,3,3] ${\displaystyle {\stackrel{}{B}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$ [4,3,31,1] ${\displaystyle {\stackrel{}{C}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$ [4,3,3,4] ${\displaystyle {\stackrel{}{D}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$ [31,1,1,1]
특성.	정점 전이

4차원 유클리드 기하학에서 잘린 24셀 벌집합은 균일한 공간을 채우는 벌집합이다.그것은 테서락트와 잘린 24셀의 세포를 포함하고 있는 보통의 24셀 벌집모양의 잘라낸 것으로 볼 수 있다.

그것은 스너브 24셀 벌집이라고 불리는 균일한 교대법을 가지고 있다.$D{\displaystyle {\stackrel{~}{}4}_{\mathrm{}}}$ ${\$시공에서$$ 나온 스너브 입니다.잘린 24셀에는 Schléfli 기호 t{3^1,1,1,1}가 있으며, 스너브는 s{3^1,1,1,1}로 표시된다.

대체 이름

• 잘린 이코시테트라코리아 테트라콤브
• 잘린 이코시테트라코리아 벌집
• 캔트런치 16셀 벌집
• 바이칸티트룬 갈린 큐셀틱 벌집

대칭 구조

이 테셀레이션에는 다섯 가지 다른 대칭 구조가 있다.각 대칭은 24-셀 크기의 색 잘린 24-셀 면의 서로 다른 배열로 나타낼 수 있다.모든 경우에 잘린 24세포 4개와 각 꼭지점마다 1개의 정점이 만나지만 정점 수치는 서로 다른 대칭 생성기를 가진다.

콕시터군	콕시터 도표를 만들다	면	정점수	꼭지점 형상을 나타내다 대칭 (주문)
${\displaystyle {\tilde{F}_{4}}$ = [3,4,3,3]		4: 1:		, [3,3] (24)
${\displaystyle {\tilde{F}_{4}}$ = [3,3,4,3]		3: 1: 1:		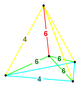, [3] (6)
${\displaystyle {\tilde{C}_{4}}$ = [4,3,3,4]		2,2: 1:		, [2] (4)
${\displaystyle {\tilde{B}_{4}}$ = [31,1,3,4]		1,1: 2: 1:		, [ ] (2)
${\displaystyle {\tilde{D}_{4}}$ = [31,1,1,1]		1,1,1,1: 1:		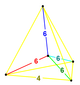[ ]+ (1)

참고 항목

4-공간의 정규 및 균일한 벌집:

• 큐테라틱 벌집
• 벌집 16셀
• 24셀 벌집
• 수정 24셀 벌집
• 스너브 24셀 벌집
• 5셀 벌집
• 잘린 5셀 벌집
• 잡동사니 5셀 벌집

참조

• Coxeter, H.S.M. 정규 폴리토페스, (3판, 1973), Dover 에디션, ISBN0-486-61480-8 페이지 296, 표 II: 일반 허니컴
• 케일리디스코어: F가 편집한 H. S. M. Coxeter의 선별된 글.아서 셔크, 피터 맥멀런, 앤서니 C.Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN978-0-471-01003-6[1]
  • (용지 24) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 III, [산술]Zeit. 200 (1988) 3-45]
• 조지 올셰프스키, 균일 파노플로이드 테트라콤브스, 원고(2006) (11개의 볼록 균일 기울기, 28개의 볼록 균일 벌집, 143개의 볼록 균일 테트라콤) 모델 99
• Klitzing, Richard. "4D Euclidean tesselations". o4x3x3x4o, x3x3x4o, x3x3x*b3x*b3x, o3o3o4x3x, x3x4o3o - ticot - O99

v t 치수 2–9의 기본 볼록 정규 및 균일한 벌집
공간	가족	${\displaystyle {\tilde{A}_{n-1}$	${\displaystyle {\tilde{C}_{n-1}$	${\displaystyle {\tilde{B}_{n-1}$	${\displaystyle {\tilde{D}_{n-1}$	${\displaystyle {\stackrel{}{G}}_{}}$~ ${\displaystyle 2_{\mathrm{}}}$ ${\$G}$$${\displaystyle {\_}_{\mathrm{}}}$2}}$$/ F ~ 4 {\$displaystyle {\tilde{F}_{4}}$ $$/ $E{\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 1_{}}$ ${\$}
E2	균일 타일링	{3[3]}	δ3	Δ3	Δ3	육각형
E3	균일볼록 벌집	{3[4]}	δ4	Δ4	Δ4
E4	제복4벌집	{3[5]}	δ5	Δ5	Δ5	24셀 벌집
E5	제복5벌집	{3[6]}	δ6	Δ6	Δ6
E6	제복6벌집	{3[7]}	δ7	Δ7	Δ7	222
E7	제복7허니콤	{3[8]}	δ8	Δ8	Δ8	133 • 331
E8	제복8벌집	{3[9]}	δ9	Δ9	Δ9	152 • 251 • 521
E9	제복9벌집	{3[10]}	δ10	Δ10	Δ10
E10	제복10벌집	{3[11]}	δ11	Δ11	Δ11
En-1	제복(n-1)-벌집합	{3[n]}	δn	Δn	Δn	1k2 • 2k1 • k21