정류정격 벌집

쿼터 큐빅 벌집
(이미지 없음)
유형	제복4벌집
가족	쿼터 고농축 벌집
슐레플리 기호	r{4,3,4} r{4,31,1} r{4,31,1} q{4,3,4}
콕시터-딘킨 도표	= = = =
4면형	h{4,32}, h3{4,32},
세포형	{3,3}, t1{4,3},
얼굴형	{3} {4}
에지 피겨	사각 피라미드
정점수	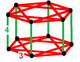길어진 {3,4}×{}
콕시터군	${\displaystyle {\stackrel{}{C}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$ $$= [4,3,3,4] ${\displaystyle {\stackrel{}{B}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$ = [4,31,1] ${\displaystyle {\stackrel{}{D}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$ $$= [31,1,1,1]
이중
특성.	정점 변환의

4차원 유클리드 기하학에서 정류된 큐트한 큐트한 테셀레이션(또는 벌집)은 유클리드 4-공간에서 균일한 공간을 채우는 테셀레이션(또는 벌집)이다.그것은 모든 원래의 가장자리 가운데에 새로운 정점을 만들고, 세포를 정류된 정점으로 수정하며, 원래의 정점에 새로운 16-셀 면을 추가하는 정점 벌집형의 정점에 의해 구성된다.그것의 꼭지점 모양은 팔면 프리즘으로, {3,4}×{}}.

4데미큐빅 벌집 반정도의 정점, 4데미큐빅 벌집 반정점, 4분의 1정도의 정점을 가지고 있어 사방정벌집이라고도 한다.^[1]

관련 허니컴

[4,3,3,4] , Coxeter 그룹은 31개의 균일한 테셀레이션 순열을 생성하며, 대칭이 뚜렷한 21개, 기하가 뚜렷한 20개를 생성한다.확장된 큐빅 벌집(stericated texteractic honeycomb라고도 함)은 큐빅 벌집과 기하학적으로 동일하다.대칭 꿀콤 중 3개는 [3,4,3,3] 계열에서 공유된다.두 차례 교대(13)와 (17)와 사분오차(2)는 다른 가족에서도 반복된다.

C4 허니컴
확장됨 대칭	확장됨 도표를 만들다	주문	허니컴스
[4,3,3,4]:		×1	1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13
[[4,3,3,4]]		×2	(1), (2), (13), 18 (6), 19, 20
[(3,3)[1+,4,3,3,4,1+]] ↔ [(3,3)[31,1,1,1]] ↔ [3,4,3,3]	↔ ↔	×6	14, 15, 16, 17

[4,3,3^1,1], , Coxeter 그룹은 31개의 균일한 테셀레이션 순열을 생성하며, 대칭이 뚜렷한 23개, 형상이 뚜렷한 4개를 생성한다.교대형식은 두 가지가 있는데, 교대형(19)과 (24)는 각각 16셀 벌집과 24셀 벌집형, 스너브 24셀 벌집형이다.

B4 허니컴
확장됨 대칭	확장됨 도표를 만들다	주문	허니컴스
[4,3,31,1]:		×1	5, 6, 7, 8
<[4,3,31,1]>: ↔[4,3,3,4]	↔	×2	9, 10, 11, 12, 13, 14, (10), 15, 16, (13), 17, 18, 19
[3[1+,4,3,31,1]] ↔ [3[3,31,1,1]] ↔ [3,3,4,3]	↔ ↔	×3	1, 2, 3, 4
[(3,3)[1+,4,3,31,1]] ↔ [(3,3)[31,1,1,1]] ↔ [3,4,3,3]	↔ ↔	×12	20, 21, 22, 23

${\displaystyle D_{\mathrm{}}}$ ${\displaystyle {\stackrel{}{~}}_{}}$ 4 {\displaystyle ${\tilde{D}_{4}}$ Coxeter$$ 그룹에 의해 구성된 균일한 벌집형 10개가 있으며, 모두 확장 대칭에 의해 다른 패밀리에서 반복되며, Coxeter-Dynkin 다이어그램의 고리의 그래프 대칭에서 볼 수 있다.10번째는 교대로 건설된다.Coxeter 표기법에서 부분군: [3,4,(3,^*3)] (지수 24), [3,4,3^*] (지수 6), [1⁺,4,3,3,4,1⁺] (지수 4), [3,4^1,1,1⁺] (지수 2)는 모두 [3^1,1,1,1]에 이형이다.

10개의 순열은 대칭 관계가 가장 높은 것으로 나열된다.

D4 허니컴
확장됨 대칭	확장됨 도표를 만들다	확장됨 무리를 짓다	허니컴스
[31,1,1,1]		${\displaystyle {\tilde{D}_{4}}$	(iii)
<[31,1,1,1]> ↔ [31,1,3,4]	↔	${\displaystyle {\stackrel{}{D}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$×2 =${\displaystyle {\stackrel{}{}}_{}}B{\displaystyle {\stackrel{}{}}_{}}$ ~ ${\displaystyle 4_{\mathrm{}}}${\$displaystyle${\$tilde{B}}_{4}}$	(iii)
<2[1,131,1]> ↔ [4,3,3,4]	↔	${\displaystyle {\stackrel{}{D}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\displaystyle {D}_{4}$ $\times$4 = $C{\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$	1, 2
[3[3,31,1,1]] ↔ [3,3,4,3]	↔	${\displaystyle {\stackrel{}{D}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$×6 =${\displaystyle {\stackrel{}{}}_{}}F{\displaystyle {\stackrel{}{}}_{}}$ ~ ${\displaystyle 4_{\mathrm{}}}${\$displaystyle${\$tilde{F}_{4}}$	3, 4, 5, 6
[4[1,131,1]] ↔ [[4,3,3,4]]	↔	${\displaystyle {\stackrel{}{D}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$×8 = $C{\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$ $\times$2	7, 8, 9
[(3,3)[31,1,1,1]] ↔ [3,4,3,3]	↔	${\displaystyle {\stackrel{}{}}_{}}$$D$${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\displaystyle {D}_{4}$ $\times$24 = $F{\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$ {$F}_{4}}$
[(3,3)[31,1,1,1]]+ ↔ [3+,4,3,3]	↔	½ ${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 4_{\mathrm{}}}$ ${\$24 = ${\displaystyle {½}_{\mathrm{}}}$ ${\displaystyle {\stackrel{}{}}_{}}$~ 4 ${\$	10

참고 항목

4-공간의 정규 및 균일한 벌집:

• 큐테라틱 벌집
• 단층 벌집
• 24셀 벌집
• 잘린 24셀 벌집
• 스너브 24셀 벌집
• 5셀 벌집
• 잘린 5셀 벌집
• 잡동사니 5셀 벌집

메모들

참조

• 케일리디스코어: F가 편집한 H. S. M. Coxeter의 선별된 글.아서 셔크, 피터 맥멀런, 앤서니 C.Thompson, Asia Ivic Weiss, Wiley-Interscience Public, 1995년 ISBN978-0-471-01003-6[1]
  • (용지 24) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 III, [산술]Zeit. 200 (1988) 3-45] p318 [2] 참조
• 조지 올셰프스키, 균일 파노플로이드 테트라콤브스, 원고(2006) (11개의 볼록 균일 기울기, 28개의 볼록 균일 벌집, 143개의 볼록 균일 테트라콤 목록)
• Klitzing, Richard. "4D Euclidean tesselations#4D". o4x3o3o4o, o3o3o *b3x4o, x3o3x *b3o4o, x3o3x *b3o - ritt - O87
• Conway JH, Sloane NJH (1998). Sphere Packings, Lattices and Groups (3rd ed.). ISBN 0-387-98585-9.

v t 치수 2–9의 기본 볼록 정규 및 균일한 벌집
공간	가족	${\displaystyle {\tilde{A}_{n-1}$	${\displaystyle {\tilde{C}_{n-1}$	${\displaystyle {\tilde{B}_{n-1}$	${\displaystyle {\tilde{D}_{n-1}$	${\displaystyle {\stackrel{}{G}}_{}}$~ ${\displaystyle 2_{\mathrm{}}}$ ${\$G}$$${\displaystyle {\_}_{\mathrm{}}}$2}}$$/ F ~ 4 {\$displaystyle {\tilde{F}_{4}}$ $$/ $E{\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 1_{}}$ ${\$}
E2	균일 타일링	{3[3]}	δ3	Δ3	Δ3	육각형
E3	균일볼록 벌집	{3[4]}	δ4	Δ4	Δ4
E4	제복4벌집	{3[5]}	δ5	Δ5	Δ5	24셀 벌집
E5	제복5벌집	{3[6]}	δ6	Δ6	Δ6
E6	제복6벌집	{3[7]}	δ7	Δ7	Δ7	222
E7	제복7허니콤	{3[8]}	δ8	Δ8	Δ8	133 • 331
E8	제복8벌집	{3[9]}	δ9	Δ9	Δ9	152 • 251 • 521
E9	제복9벌집	{3[10]}	δ10	Δ10	Δ10
E10	제복10벌집	{3[11]}	δ11	Δ11	Δ11
En-1	제복(n-1)-벌집합	{3[n]}	δn	Δn	Δn	1k2 • 2k1 • k21