균일한 9-폴리토프

세 개의 규칙적이고 관련된 균일한 폴리토피 그래프

9차원 기하학에서 9차원 폴리토프 또는 9-폴리토프는 8-폴리토프 패싯에 포함되는 폴리토프이다.각 7 폴리토프 능선은 정확히 2개의 8 폴리토프 패싯에 의해 공유됩니다.

균일한 9-폴리토프는 정점 추이성이며 균일한 8-폴리토프면으로 구성된다.

표준 9-폴리토프

정규 9-폴리토프는 각 피크 주위에 {p,q,r,s,t,u,v}개의 8-폴리토프 패스가 있는 슐래플리 기호 {p,q,r,s,t,u,w}로 나타낼 수 있습니다.

이러한 볼록 정규 9-폴리토프는 정확히 3가지입니다.

{3,3,3,3,3,3,3} - 9-199x
{4,3,3,3,3,3,3,3} - 9-큐브
{3,3,3,3,3,4} - 9 - 직교

볼록하지 않은 일반 9-폴리토프는 없습니다.

오일러 특성

주어진 9-폴리토프의 토폴로지는 베티 수 및 비틀림 ^[1]계수에 의해 정의됩니다.

다면체를 특징짓는 데 사용되는 오일러 특성의 값은 기본 위상이 무엇이든 간에 더 높은 차원으로 유용하게 일반화되지 않습니다.이러한 오일러 특성의 불충분함은 ^[1]더 정교한 베티 수 발견으로 이어졌다.

마찬가지로, 다면체의 방향성의 개념은 트로이덜 폴리톱의 표면 비틀림을 특징짓기에는 불충분하며, 이는 비틀림 ^[1]계수의 사용으로 이어졌다.

기본 콕서터군별 균일한 9-폴리토피스

반사 대칭을 갖는 균일한 9-폴리토프는 콕서터-다인킨 다이어그램의 링 순열로 표현되는 이 세 가지 콕서터 그룹에 의해 생성될 수 있다.

콕서터군		콕서터-딘킨 도표
A₉.	[3⁸]
B₉.	[4,3⁷]
D₉.	[3^6,1,1]

각 패밀리에서 선택한 정규 및 균일한 9-폴리토프는 다음과 같습니다.

심플렉스 패밀리:A₉ [ 3⁸ ] -
- 271개의 균일한 9-폴리토프(그룹 다이어그램의 링 순열)로, 1개의 정칙이 포함됩니다.
  1. {3⁸} - 9-backx 또는 deca-9-tope 또는 decayotton -
Hypercube/orthoplex 패밀리: B₉ [4,3⁸] -
- 511개의 균일한 9-폴리토프는 그룹 다이어그램의 링 순열로서, 2개의 정규 폴리토프를 포함한다.
  1. {4,3⁷} - 9-입방체 또는 Enneract -
  2. {3⁷,4} - 9-정압 또는 enneacross -
Demihypercube₉ D 패밀리: [3^6,1,1] -
- 383 그룹 다이어그램의 링 순열로서 다음을 포함한 균일한 9-폴리토프:
  1. {3^1,6,1} - 9-demicube 또는 demieneract, 1-₆₁; h{4,3⁸}라고도 합니다.
  2. {3^6,1,1} - 9-정압, 6-₁₁

A가족₉

A 제품군의 대칭₉ 차수는 3628800(10 요인)입니다.

하나 이상의 고리를 가진 콕서터-다인킨 다이어그램의 모든 배열에 기초한 256+16-1=271 형태가 있다.이것들은 모두 아래에 열거되어 있습니다.Bowers 스타일의 머리글자 이름은 상호 참조를 위해 괄호로 둘러싸여 있습니다.

#	그래프	콕서터-딘킨 도표 슐레플리 기호 이름.	요소수
#	그래프	콕서터-딘킨 도표 슐레플리 기호 이름.	8면	7면	6면	5면	4면	셀	얼굴	가장자리	꼭지점
1		t₀{3,3,3,3,3,3,3,3,3,3} 9-165x(일)	10	45	120	210	252	210	120	45	10
2		t₁{3,3,3,3,3,3,3,3,3,3} 수정 완료 9-심플렉스(재일)								360	45
3		t₂{3,3,3,3,3,3,3,3,3,3} 양방향 9-심플렉스(브라이드)								1260	120
4		t₃{3,3,3,3,3,3,3,3,3,3} Triorrectized 9-simplex(트레이)								2520	210
5		t₄{3,3,3,3,3,3,3,3,3,3} 4배정형 9심플렉스(icoy								3150	252
6		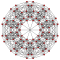t_0,1{3,3,3,3,3,3,3,3,3,3} 잘라낸 9-심플렉스(수요일)								405	90
7		t_0,2{3,3,3,3,3,3,3,3,3,3} 9개의 심플렉스(cantellated								2880	360
8		t_1,2{3,3,3,3,3,3,3,3,3,3} 비트런컷된9 심플렉스								1620	360
9		t_0,3{3,3,3,3,3,3,3,3,3,3} Runcated 9 심플렉스								8820	840
10		t_1,3{3,3,3,3,3,3,3,3,3,3} 바이칸텔레이티드9-단순								10080	1260
11		t_2,3{3,3,3,3,3,3,3,3,3,3} Tritruncuted 9-simplex(트레이데이)								3780	840
12		t_0,4{3,3,3,3,3,3,3,3,3,3} 입체화 9-심플렉스								15120	1260
13		t_1,4{3,3,3,3,3,3,3,3,3,3} Biruncated 9-simplex								26460	2520
14		t_2,4{3,3,3,3,3,3,3,3,3,3} 트리칸텔레이티드9-단순								20160	2520
15		t_3,4{3,3,3,3,3,3,3,3,3,3} 사각형으로 잘라진 9-단순수								5670	1260
16		t_0,5{3,3,3,3,3,3,3,3,3,3} 펜텔레이티드 9-심플렉스								15750	1260
17		t_1,5{3,3,3,3,3,3,3,3,3,3} 바이스터리케이트 9-심플렉스								37800	3150
18		t_2,5{3,3,3,3,3,3,3,3,3,3} 트리런케이티드9 심플렉스								44100	4200
19		t_3,5{3,3,3,3,3,3,3,3,3,3} 사각형 9-심플렉스								25200	3150
20		t_0,6{3,3,3,3,3,3,3,3,3,3} 9단독화								10080	840
21		t_1,6{3,3,3,3,3,3,3,3,3,3} 이관절형 9단축								31500	2520
22		t_2,6{3,3,3,3,3,3,3,3,3,3} 트리스테리케이트 9-심플렉스								50400	4200
23		t_0,7{3,3,3,3,3,3,3,3,3,3} 헵텔레이트 9-단형								3780	360
24		t_1,7{3,3,3,3,3,3,3,3,3,3} 생체독성 9-단순화								15120	1260
25		t_0,8{3,3,3,3,3,3,3,3,3,3} 옥텔레이티드 9-단순								720	90
26		t_0,1,2{3,3,3,3,3,3,3,3,3,3} 칸티트런컷된 9-단순								3240	720
27		t_0,1,3{3,3,3,3,3,3,3,3,3,3} 런시트런컷된 9-단순								18900	2520
28		t_0,2,3{3,3,3,3,3,3,3,3,3,3} 룬시칸텔레이티드9-단순								12600	2520
29		t_1,2,3{3,3,3,3,3,3,3,3,3,3} 바이칸티트런 절단 9-단순								11340	2520
30		t_0,1,4{3,3,3,3,3,3,3,3,3,3} 스테리트런 절단된 9-단순								47880	5040
31		t_0,2,4{3,3,3,3,3,3,3,3,3,3} 스테리칸텔레이티드9-단순								60480	7560
32		t_1,2,4{3,3,3,3,3,3,3,3,3,3} 비룬시트런컷 9-단순								52920	7560
33		t_0,3,4{3,3,3,3,3,3,3,3,3,3} 스테리룬산염 9-단순								27720	5040
34		t_1,3,4{3,3,3,3,3,3,3,3,3,3} 비룬시칸텔라티드9-단순								41580	7560
35		t_2,3,4{3,3,3,3,3,3,3,3,3,3} 트리칸티트런 절단된 9-단순								22680	5040
36		t_0,1,5{3,3,3,3,3,3,3,3,3,3} 펜티트런 절단된 9-단순수								66150	6300
37		t_0,2,5{3,3,3,3,3,3,3,3,3,3} 펜티칸텔레이티드 9-단순								126000	12600
38		t_1,2,5{3,3,3,3,3,3,3,3,3,3} 9-단순한 쌍관절								107100	12600
39		t_0,3,5{3,3,3,3,3,3,3,3,3,3} 펜티런산염 9-심플렉스								107100	12600
40		t_1,3,5{3,3,3,3,3,3,3,3,3,3} 비스테리칸텔라티드9-단순								151200	18900
41		t_2,3,5{3,3,3,3,3,3,3,3,3,3} 트리룬시트런컷 9-단순								81900	12600
42		t_0,4,5{3,3,3,3,3,3,3,3,3,3} 펜티스터화 9-심플렉스								37800	6300
43		t_1,4,5{3,3,3,3,3,3,3,3,3,3} 비스테리룬산염 9-심플렉스								81900	12600
44		t_2,4,5{3,3,3,3,3,3,3,3,3,3} 트리룬시칸텔라티드9-단순								75600	12600
45		t_3,4,5{3,3,3,3,3,3,3,3,3,3} 사각형으로 절단된 9-심플렉스								28350	6300
46		t_0,1,6{3,3,3,3,3,3,3,3,3,3} 헥시트런컷된 9-단순								52920	5040
47		t_0,2,6{3,3,3,3,3,3,3,3,3,3} 헥시칸텔레이티드9-단순								138600	12600
48		t_1,2,6{3,3,3,3,3,3,3,3,3,3} 2엔트런 절단된 9심플렉스								113400	12600
49		t_0,3,6{3,3,3,3,3,3,3,3,3,3} 헥시룬산9 심플렉스								176400	16800
50		t_1,3,6{3,3,3,3,3,3,3,3,3,3} 이원추형 9단축								239400	25200
51		t_2,3,6{3,3,3,3,3,3,3,3,3,3} 9-단순 트리스테리트런 절단								126000	16800
52		t_0,4,6{3,3,3,3,3,3,3,3,3,3} 6진법 9심플렉스								113400	12600
53		t_1,4,6{3,3,3,3,3,3,3,3,3,3} Bipentiruncated 9-simplex								226800	25200
54		t_2,4,6{3,3,3,3,3,3,3,3,3,3} 트리스테리칸텔라티드9-단순								201600	25200
55		t_0,5,6{3,3,3,3,3,3,3,3,3,3} 헥시펜텔레이트 9-단순								32760	5040
56		t_1,5,6{3,3,3,3,3,3,3,3,3,3} 바이펜티스터리케이트9 심플렉스								94500	12600
57		t_0,1,7{3,3,3,3,3,3,3,3,3,3} 헵티트런컷 9-단순								23940	2520
58		t_0,2,7{3,3,3,3,3,3,3,3,3,3} 헵탄텔화 9단순								83160	7560
59		t_1,2,7{3,3,3,3,3,3,3,3,3,3} Bihexitruncuted 9-simplex								64260	7560
60		t_0,3,7{3,3,3,3,3,3,3,3,3,3} 헵티룬산염 9-심플렉스								144900	12600
61		t_1,3,7{3,3,3,3,3,3,3,3,3,3} 바이헥시칸텔라티드9-단순								189000	18900
62		t_0,4,7{3,3,3,3,3,3,3,3,3,3} 헵티스테이티드9 심플렉스								138600	12600
63		t_1,4,7{3,3,3,3,3,3,3,3,3,3} Bihexiruncated 9-simplex								264600	25200
64		t_0,5,7{3,3,3,3,3,3,3,3,3,3} 헵티펜텔화9-단순화								71820	7560
65		t_0,6,7{3,3,3,3,3,3,3,3,3,3} 헵티헥시드9-단순화								17640	2520
66		t_0,1,8{3,3,3,3,3,3,3,3,3,3} 옥티트런 절단된 9-단순								5400	720
67		t_0,2,8{3,3,3,3,3,3,3,3,3,3} 옥티칸텔레이티드9-단순								25200	2520
68		t_0,3,8{3,3,3,3,3,3,3,3,3,3} 옥티런치 9 심플렉스								57960	5040
69		t_0,4,8{3,3,3,3,3,3,3,3,3,3} 옥티스터리케이트9 심플렉스								75600	6300
70		t_0,1,2,3{3,3,3,3,3,3,3,3,3,3} 룬치칸트런컷된 9-단순								22680	5040
71		t_0,1,2,4{3,3,3,3,3,3,3,3,3,3} 스테리칸티트런컷된9-단순화								105840	15120
72		t_0,1,3,4{3,3,3,3,3,3,3,3,3,3} 스테리룬시트루티드9-단순화								75600	15120
73		t_0,2,3,4{3,3,3,3,3,3,3,3,3,3} 스테리룬시칸텔화9-단순화								75600	15120
74		t_1,2,3,4{3,3,3,3,3,3,3,3,3,3} Biruncicantitruncuted 9-simplex								68040	15120
75		t_0,1,2,5{3,3,3,3,3,3,3,3,3,3} 펜티칸티트런 절단 9-단순								214200	25200
76		t_0,1,3,5{3,3,3,3,3,3,3,3,3,3} Pentiruncitruncuted 9-simplex								283500	37800
77		t_0,2,3,5{3,3,3,3,3,3,3,3,3,3} 펜티룬시칸텔화 9-단순화								264600	37800
78		t_1,2,3,5{3,3,3,3,3,3,3,3,3,3} 9-단순화 바이스테리칸티트런 절단								245700	37800
79		t_0,1,4,5{3,3,3,3,3,3,3,3,3,3} 펜티스터릿컷 9-단순								138600	25200
80		t_0,2,4,5{3,3,3,3,3,3,3,3,3,3} 펜티스테리칸텔라티드9-단순								226800	37800
81		t_1,2,4,5{3,3,3,3,3,3,3,3,3,3} 비스테리룬시트루티드9-단순화								189000	37800
82		t_0,3,4,5{3,3,3,3,3,3,3,3,3,3} 펜티스테리루네이트 9-단순								138600	25200
83		t_1,3,4,5{3,3,3,3,3,3,3,3,3,3} 비스테리룬시칸텔화 9-단순화								207900	37800
84		t_2,3,4,5{3,3,3,3,3,3,3,3,3,3} 트리런치칸트런 9-단순화								113400	25200
85		t_0,1,2,6{3,3,3,3,3,3,3,3,3,3} 헥시칸티트런컷 9-단순								226800	25200
86		t_0,1,3,6{3,3,3,3,3,3,3,3,3,3} 헥시룬시트런컷 9-단순								453600	50400
87		t_0,2,3,6{3,3,3,3,3,3,3,3,3,3} 헥시룬시칸텔화 9-단순화								403200	50400
88		t_1,2,3,6{3,3,3,3,3,3,3,3,3,3} 바이펜티칸트런컷 9-단순								378000	50400
89		t_0,1,4,6{3,3,3,3,3,3,3,3,3,3} 육진법 9-단순법								403200	50400
90		t_0,2,4,6{3,3,3,3,3,3,3,3,3,3} 육면체의 9단순								604800	75600
91		t_1,2,4,6{3,3,3,3,3,3,3,3,3,3} Bipentiruncitruncated 9-simplex								529200	75600
92		t_0,3,4,6{3,3,3,3,3,3,3,3,3,3} 헥시스테리루네이트 9-단순								352800	50400
93		t_1,3,4,6{3,3,3,3,3,3,3,3,3,3} Bipentiruncicantellated 9-simplex								529200	75600
94		t_2,3,4,6{3,3,3,3,3,3,3,3,3,3} 트리스테리칸티트런컷 9-단순								302400	50400
95		t_0,1,5,6{3,3,3,3,3,3,3,3,3,3} 육각 비트런 절단 9-단순								151200	25200
96		t_0,2,5,6{3,3,3,3,3,3,3,3,3,3} 헥시펜티칸텔레이티드9-단순								352800	50400
97		t_1,2,5,6{3,3,3,3,3,3,3,3,3,3} 바이펜티스테리트런컷 9-단순								277200	50400
98		t_0,3,5,6{3,3,3,3,3,3,3,3,3,3} 헥시펜티룬산염 9-단순								352800	50400
99		t_1,3,5,6{3,3,3,3,3,3,3,3,3,3} 바이펜티스테리칸텔라티드9-단순								491400	75600
100		t_2,3,5,6{3,3,3,3,3,3,3,3,3,3} Tristeriruncitruncuted 9-simplex								252000	50400
101		t_0,4,5,6{3,3,3,3,3,3,3,3,3,3} 6진법 9심플렉스								151200	25200
102		t_1,4,5,6{3,3,3,3,3,3,3,3,3,3} 바이펜티스테리루닌화9-단순화								327600	50400
103		t_0,1,2,7{3,3,3,3,3,3,3,3,3,3} 햅틱안티트런컷 9-단순화								128520	15120
104		t_0,1,3,7{3,3,3,3,3,3,3,3,3,3} 헵티룬시트런 9-단순화								359100	37800
105		t_0,2,3,7{3,3,3,3,3,3,3,3,3,3} 헵티룬시칸텔화9-단순화								302400	37800
106		t_1,2,3,7{3,3,3,3,3,3,3,3,3,3} 생체독성제 9단순화								283500	37800
107		t_0,1,4,7{3,3,3,3,3,3,3,3,3,3} 헵티스테리트런컷 9-단순								478800	50400
108		t_0,2,4,7{3,3,3,3,3,3,3,3,3,3} 헵티스테리칸텔라티드9-단순								680400	75600
109		t_1,2,4,7{3,3,3,3,3,3,3,3,3,3} Bihexiruncitruncated 9-simplex								604800	75600
110		t_0,3,4,7{3,3,3,3,3,3,3,3,3,3} 헵티스테리룬산염 9-단순								378000	50400
111		t_1,3,4,7{3,3,3,3,3,3,3,3,3,3} 비헥시룬시칸텔화 9-단순화								567000	75600
112		t_0,1,5,7{3,3,3,3,3,3,3,3,3,3} 헵티펜티트런컷 9-단순화								321300	37800
113		t_0,2,5,7{3,3,3,3,3,3,3,3,3,3} 헵티펜티칸텔화9-단순화								680400	75600
114		t_1,2,5,7{3,3,3,3,3,3,3,3,3,3} 바이헥시스테리트런치 9-단순								567000	75600
115		t_0,3,5,7{3,3,3,3,3,3,3,3,3,3} 헵티펜티룬산염 9-단순								642600	75600
116		t_1,3,5,7{3,3,3,3,3,3,3,3,3,3} 비헥시스테리칸텔라티드9-단순								907200	113400
117		t_0,4,5,7{3,3,3,3,3,3,3,3,3,3} 헵티펜티스테리케이트 9-단순화								264600	37800
118		t_0,1,6,7{3,3,3,3,3,3,3,3,3,3} 헵티헥시트가 9-단순화								98280	15120
119		t_0,2,6,7{3,3,3,3,3,3,3,3,3,3} 헵티옥시칸텔화9-단순								302400	37800
120		t_1,2,6,7{3,3,3,3,3,3,3,3,3,3} Bihexipentitruncuted 9-simplex								226800	37800
121		t_0,3,6,7{3,3,3,3,3,3,3,3,3,3} 헵티헥시룬산염 9-단순								428400	50400
122		t_0,4,6,7{3,3,3,3,3,3,3,3,3,3} 헵티헥시스테리케이트 9-단순화								302400	37800
123		t_0,5,6,7{3,3,3,3,3,3,3,3,3,3} 헵티헥시펜텔화 9-단순화								98280	15120
124		t_0,1,2,8{3,3,3,3,3,3,3,3,3,3} 옥티칸티트런 절단 9-단순								35280	5040
125		t_0,1,3,8{3,3,3,3,3,3,3,3,3,3} 옥티룬시트런컷9-단순								136080	15120
126		t_0,2,3,8{3,3,3,3,3,3,3,3,3,3} 옥티런시칸텔라티드9-단순								105840	15120
127		t_0,1,4,8{3,3,3,3,3,3,3,3,3,3} 옥티스터릿컷 9-단순								252000	25200
128		t_0,2,4,8{3,3,3,3,3,3,3,3,3,3} 옥시스테리칸텔라티드9-단순								340200	37800
129		t_0,3,4,8{3,3,3,3,3,3,3,3,3,3} 옥티스터리루네이트 9-단순								176400	25200
130		t_0,1,5,8{3,3,3,3,3,3,3,3,3,3} 옥티펜티트런 절단 9-단순								252000	25200
131		t_0,2,5,8{3,3,3,3,3,3,3,3,3,3} 옥티펜티칸텔라티드9-단순								504000	50400
132		t_0,3,5,8{3,3,3,3,3,3,3,3,3,3} 옥티펜티루네이트 9-심플렉스								453600	50400
133		t_0,1,6,8{3,3,3,3,3,3,3,3,3,3} Octihexitruncated 9-simplex								136080	15120
134		t_0,2,6,8{3,3,3,3,3,3,3,3,3,3} 옥티옥시칸텔라티드9-단순								378000	37800
135		t_0,1,7,8{3,3,3,3,3,3,3,3,3,3} 옥티펩티드 9-단순화								35280	5040
136		t_0,1,2,3,4{3,3,3,3,3,3,3,3,3,3} 스테리룬시칸트런컷 9-단순화								136080	30240
137		t_0,1,2,3,5{3,3,3,3,3,3,3,3,3,3} 펜티런시칸트런컷 9-단순화								491400	75600
138		t_0,1,2,4,5{3,3,3,3,3,3,3,3,3,3} 펜티스테리칸티트런컷 9-단순								378000	75600
139		t_0,1,3,4,5{3,3,3,3,3,3,3,3,3,3} Pentisteriruncitruncuted 9-simplex								378000	75600
140		t_0,2,3,4,5{3,3,3,3,3,3,3,3,3,3} 펜티스터리런시칸텔화 9-단순화								378000	75600
141		t_1,2,3,4,5{3,3,3,3,3,3,3,3,3,3} 비스테리룬시칸티트런 9단순								340200	75600
142		t_0,1,2,3,6{3,3,3,3,3,3,3,3,3,3} 헥시런시칸티트런 9-단순화								756000	100800
143		t_0,1,2,4,6{3,3,3,3,3,3,3,3,3,3} 육각형 절단 9-단순								1058400	151200
144		t_0,1,3,4,6{3,3,3,3,3,3,3,3,3,3} 헥시스터리런시트 절단 9-단순								982800	151200
145		t_0,2,3,4,6{3,3,3,3,3,3,3,3,3,3} 헥시스터리룬시칸텔화 9-단순화								982800	151200
146		t_1,2,3,4,6{3,3,3,3,3,3,3,3,3,3} Bipentiruncicantruncuted 9-simplex								907200	151200
147		t_0,1,2,5,6{3,3,3,3,3,3,3,3,3,3} 헥시펜티칸티크루티드9-단순								554400	100800
148		t_0,1,3,5,6{3,3,3,3,3,3,3,3,3,3} 헥시펜티룬시트화9-단순화								907200	151200
149		t_0,2,3,5,6{3,3,3,3,3,3,3,3,3,3} 헥시펜티룬시칸텔화9-단순화								831600	151200
150		t_1,2,3,5,6{3,3,3,3,3,3,3,3,3,3} 바이펜티스테리칸티트런컷 9-단순								756000	151200
151		t_0,1,4,5,6{3,3,3,3,3,3,3,3,3,3} 헥시펜티스테이트런컷 9-단순								554400	100800
152		t_0,2,4,5,6{3,3,3,3,3,3,3,3,3,3} 헥시펜티스테리칸텔라티드9-단순								907200	151200
153		t_1,2,4,5,6{3,3,3,3,3,3,3,3,3,3} Bipentisteriruncitruncated 9-simplex								756000	151200
154		t_0,3,4,5,6{3,3,3,3,3,3,3,3,3,3} 헥시펜티스테리루네이트화9-단순화								554400	100800
155		t_1,3,4,5,6{3,3,3,3,3,3,3,3,3,3} Bipentisteriruncicantellated 9-simplex								831600	151200
156		t_2,3,4,5,6{3,3,3,3,3,3,3,3,3,3} 트리스테리룬시칸트런컷 9-단순화								453600	100800
157		t_0,1,2,3,7{3,3,3,3,3,3,3,3,3,3} 헵티룬시칸트런컷 9-단순화								567000	75600
158		t_0,1,2,4,7{3,3,3,3,3,3,3,3,3,3} 헵티스테리칸티트런컷 9-단순								1209600	151200
159		t_0,1,3,4,7{3,3,3,3,3,3,3,3,3,3} 헵티스터리룬시트란컷드9-단순								1058400	151200
160		t_0,2,3,4,7{3,3,3,3,3,3,3,3,3,3} 헵티스터리룬시칸텔화9-단순화								1058400	151200
161		t_1,2,3,4,7{3,3,3,3,3,3,3,3,3,3} Bihexiruncicantitruncated 9-simplex								982800	151200
162		t_0,1,2,5,7{3,3,3,3,3,3,3,3,3,3} 헵티펜티칸티크루티드9-단순화								1134000	151200
163		t_0,1,3,5,7{3,3,3,3,3,3,3,3,3,3} 헵티펜티룬구간단화9-단순화								1701000	226800
164		t_0,2,3,5,7{3,3,3,3,3,3,3,3,3,3} 헵티펜티룬시칸텔화9-단순화								1587600	226800
165		t_1,2,3,5,7{3,3,3,3,3,3,3,3,3,3} 바이헥시스테리칸티트런 9-단순화								1474200	226800
166		t_0,1,4,5,7{3,3,3,3,3,3,3,3,3,3} 헵티펜티스터잇런컷 9-단순								982800	151200
167		t_0,2,4,5,7{3,3,3,3,3,3,3,3,3,3} 헵티펜티스테리칸텔라티드9-단순								1587600	226800
168		t_1,2,4,5,7{3,3,3,3,3,3,3,3,3,3} Bihexisteriruncitruncuted 9-simplex								1360800	226800
169		t_0,3,4,5,7{3,3,3,3,3,3,3,3,3,3} 헵티펜티스테론화9-단순화								982800	151200
170		t_1,3,4,5,7{3,3,3,3,3,3,3,3,3,3} 비헥시스터리룬시칸텔화 9-단순화								1474200	226800
171		t_0,1,2,6,7{3,3,3,3,3,3,3,3,3,3} 헵티헥시칸티크루티드9-단순화								453600	75600
172		t_0,1,3,6,7{3,3,3,3,3,3,3,3,3,3} 헵티헥시룬시트런 9-단순화								1058400	151200
173		t_0,2,3,6,7{3,3,3,3,3,3,3,3,3,3} 헵티헥시룬시칸텔화9-단순화								907200	151200
174		t_1,2,3,6,7{3,3,3,3,3,3,3,3,3,3} Bihexipenticantitruncuted 9-simplex								831600	151200
175		t_0,1,4,6,7{3,3,3,3,3,3,3,3,3,3} 헵티헥시스터잇런 9-단순								1058400	151200
176		t_0,2,4,6,7{3,3,3,3,3,3,3,3,3,3} 헵티헥시스테리칸텔화9-단순화								1587600	226800
177		t_1,2,4,6,7{3,3,3,3,3,3,3,3,3,3} Bihexipentiruncitruncuted 9-simplex								1360800	226800
178		t_0,3,4,6,7{3,3,3,3,3,3,3,3,3,3} 헵티헥시스테리루닌산9-단순								907200	151200
179		t_0,1,5,6,7{3,3,3,3,3,3,3,3,3,3} 헵티헥시펜트런컷 9-단순								453600	75600
180		t_0,2,5,6,7{3,3,3,3,3,3,3,3,3,3} 헵티헥시펜티칸텔화9-단순화								1058400	151200
181		t_0,3,5,6,7{3,3,3,3,3,3,3,3,3,3} 헵티헥시펜티룬산염 9-단순								1058400	151200
182		t_0,4,5,6,7{3,3,3,3,3,3,3,3,3,3} 헵티헥시펜티스테리케이트 9-단순화								453600	75600
183		t_0,1,2,3,8{3,3,3,3,3,3,3,3,3,3} 옥티런시칸트런컷 9-단순화								196560	30240
184		t_0,1,2,4,8{3,3,3,3,3,3,3,3,3,3} 옥시스테리칸티트런컷 9-단순								604800	75600
185		t_0,1,3,4,8{3,3,3,3,3,3,3,3,3,3} 옥티스터리런시트레이트 9-단순화								491400	75600
186		t_0,2,3,4,8{3,3,3,3,3,3,3,3,3,3} 옥티스터리런시칸텔라티드9-단순								491400	75600
187		t_0,1,2,5,8{3,3,3,3,3,3,3,3,3,3} 옥티펜티칸티크루티드9-단순								856800	100800
188		t_0,1,3,5,8{3,3,3,3,3,3,3,3,3,3} 옥티펜티룬시트화9-단순화								1209600	151200
189		t_0,2,3,5,8{3,3,3,3,3,3,3,3,3,3} 옥티펜티룬시칸텔화9-단순화								1134000	151200
190		t_0,1,4,5,8{3,3,3,3,3,3,3,3,3,3} 옥티펜티스테이트런컷 9-단순								655200	100800
191		t_0,2,4,5,8{3,3,3,3,3,3,3,3,3,3} 옥티펜티스테리칸텔라티드9-단순								1058400	151200
192		t_0,3,4,5,8{3,3,3,3,3,3,3,3,3,3} 옥티펜티스테리루네이트화9-단순								655200	100800
193		t_0,1,2,6,8{3,3,3,3,3,3,3,3,3,3} 옥티옥시칸티크루티드9-단순화								604800	75600
194		t_0,1,3,6,8{3,3,3,3,3,3,3,3,3,3} Octihexiruncitruncated 9-simplex								1285200	151200
195		t_0,2,3,6,8{3,3,3,3,3,3,3,3,3,3} 옥티헥시룬시칸텔화9-단순화								1134000	151200
196		t_0,1,4,6,8{3,3,3,3,3,3,3,3,3,3} 옥티헥시스테리트런치 9-단순								1209600	151200
197		t_0,2,4,6,8{3,3,3,3,3,3,3,3,3,3} 옥티헥시스테리칸텔라티드9-단순								1814400	226800
198		t_0,1,5,6,8{3,3,3,3,3,3,3,3,3,3} 옥티헥시펜트런컷 9-단순								491400	75600
199		t_0,1,2,7,8{3,3,3,3,3,3,3,3,3,3} 옥티헥티안티트런컷된 9-단순								196560	30240
200		t_0,1,3,7,8{3,3,3,3,3,3,3,3,3,3} 옥티펩티룬시트룬 9-단순화								604800	75600
201		t_0,1,4,7,8{3,3,3,3,3,3,3,3,3,3} 옥티프리스테리트레이트 9-단순화								856800	100800
202		t_0,1,2,3,4,5{3,3,3,3,3,3,3,3,3,3} Pentisteriruncicantruncuted 9-simplex								680400	151200
203		t_0,1,2,3,4,6{3,3,3,3,3,3,3,3,3,3} 헥시스터리런시칸티트런컷 9-단순								1814400	302400
204		t_0,1,2,3,5,6{3,3,3,3,3,3,3,3,3,3} 헥시펜티룬시칸티트런 9-단순화								1512000	302400
205		t_0,1,2,4,5,6{3,3,3,3,3,3,3,3,3,3} 헥시펜티스테리칸티트런컷 9-단순								1512000	302400
206		t_0,1,3,4,5,6{3,3,3,3,3,3,3,3,3,3} 헥시펜티스테리룬시트화9-단순화								1512000	302400
207		t_0,2,3,4,5,6{3,3,3,3,3,3,3,3,3,3} 헥시펜티스터리룬시칸텔화9-단순화								1512000	302400
208		t_1,2,3,4,5,6{3,3,3,3,3,3,3,3,3,3} Bipentisteriruncicantruncated 9-simplex								1360800	302400
209		t_0,1,2,3,4,7{3,3,3,3,3,3,3,3,3,3} 헵티스터리룬시칸티트런컷 9-단순화								1965600	302400
210		t_0,1,2,3,5,7{3,3,3,3,3,3,3,3,3,3} 헵티펜티룬시칸티트런 9-단순화								2948400	453600
211		t_0,1,2,4,5,7{3,3,3,3,3,3,3,3,3,3} 헵티펜티스테리칸티트런 9-단순화								2721600	453600
212		t_0,1,3,4,5,7{3,3,3,3,3,3,3,3,3,3} 헵티펜티스테룬시트런 9-단순화								2721600	453600
213		t_0,2,3,4,5,7{3,3,3,3,3,3,3,3,3,3} 헵티펜티스테룬시칸텔화9-단순화								2721600	453600
214		t_1,2,3,4,5,7{3,3,3,3,3,3,3,3,3,3} Bihexisteriruncicantitruncuted 9-simplex								2494800	453600
215		t_0,1,2,3,6,7{3,3,3,3,3,3,3,3,3,3} 헵티헥시룬시칸티트런 9단순								1663200	302400
216		t_0,1,2,4,6,7{3,3,3,3,3,3,3,3,3,3} 헵티헥시스테리칸티트런 9-단순화								2721600	453600
217		t_0,1,3,4,6,7{3,3,3,3,3,3,3,3,3,3} 헵티헥시스테리룬시트레이트 9-단순								2494800	453600
218		t_0,2,3,4,6,7{3,3,3,3,3,3,3,3,3,3} 헵티헥시스테룬시칸텔화9-단순화								2494800	453600
219		t_1,2,3,4,6,7{3,3,3,3,3,3,3,3,3,3} Bihexipentiruncicantitruncated 9-simplex								2268000	453600
220		t_0,1,2,5,6,7{3,3,3,3,3,3,3,3,3,3} 헵티헥시펜티칸티칸티칸티칸티칸티칸티칸티칸티칸티칸티칸티칸티칸티칸티칸								1663200	302400
221		t_0,1,3,5,6,7{3,3,3,3,3,3,3,3,3,3} 헵티헥시펜티룬시트락토9-단순								2721600	453600
222		t_0,2,3,5,6,7{3,3,3,3,3,3,3,3,3,3} 헵티헥시펜티룬시칸텔화9-단순화								2494800	453600
223		t_1,2,3,5,6,7{3,3,3,3,3,3,3,3,3,3} 비헥시펜티스테리칸티트런컷 9-단순								2268000	453600
224		t_0,1,4,5,6,7{3,3,3,3,3,3,3,3,3,3} 헵티헥시펜티스테리컷 9-단순								1663200	302400
225		t_0,2,4,5,6,7{3,3,3,3,3,3,3,3,3,3} 헵티헥시펜티칸텔화9-단순화								2721600	453600
226		t_0,3,4,5,6,7{3,3,3,3,3,3,3,3,3,3} 헵티헥시펜티리스테룬산염 9-단순								1663200	302400
227		t_0,1,2,3,4,8{3,3,3,3,3,3,3,3,3,3} 옥티스터리런시칸트런컷 9-단순								907200	151200
228		t_0,1,2,3,5,8{3,3,3,3,3,3,3,3,3,3}								2116800	302400
229		t_0,1,2,4,5,8{3,3,3,3,3,3,3,3,3,3} 9-simplex								1814400	302400
230		t_0,1,3,4,5,8{3,3,3,3,3,3,3,3,3,3}								1814400	302400
231		t_0,2,3,4,5,8{3,3,3,3,3,3,3,3,3,3} 9-단순화								1814400	302400
232		t_0,1,2,3,6,8{3,3,3,3,3,3,3,3,3,3} 9-simplex --9-simplex oct oct oct--9- oct oct oct oct oct oct oct oct oct oct oct oct oct oct oct oct oct oct oct oct oct oct								2116800	302400
233		t_0,1,2,4,6,8{3,3,3,3,3,3,3,3,3,3} 9-단순화								3175200	453600
234		t_0,1,3,4,6,8{3,3,3,3,3,3,3,3,3,3} 9-simplex 9-contracted								2948400	453600
235		t_0,2,3,4,6,8{3,3,3,3,3,3,3,3,3,3} 9-단순화								2948400	453600
236		t_0,1,2,5,6,8{3,3,3,3,3,3,3,3,3,3} 9-simplex - oct--9-순 oct oct oct oct oct oct oct oct oct oct oct9-단순 oct oct oct oct oct oct oct oct oct oct oct oct								1814400	302400
237		t_0,1,3,5,6,8{3,3,3,3,3,3,3,3,3,3} 9-단순 옥티헥시펜티룬시트형 9-단순								2948400	453600
238		t_0,2,3,5,6,8{3,3,3,3,3,3,3,3,3,3} 9-단순화								2721600	453600
239		t_0,1,4,5,6,8{3,3,3,3,3,3,3,3,3,3}								1814400	302400
240		t_0,1,2,3,7,8{3,3,3,3,3,3,3,3,3,3} 9-simplex 9-simplex								907200	151200
241		t_0,1,2,4,7,8{3,3,3,3,3,3,3,3,3,3} 9-단순화								2116800	302400
242		t_0,1,3,4,7,8{3,3,3,3,3,3,3,3,3,3} 9-simplex								1814400	302400
243		t_0,1,2,5,7,8{3,3,3,3,3,3,3,3,3,3} 9-simplex								2116800	302400
244		t_0,1,3,5,7,8{3,3,3,3,3,3,3,3,3,3} 9-simplex 9-simplex								3175200	453600
245		t_0,1,2,6,7,8{3,3,3,3,3,3,3,3,3,3} 옥티헥시칸티옥시칸티클라우티드9-단순화								907200	151200
246		t_{0,1,2,3,4,5,6}{3,3,3,3,3,3,3,3,3,3} 헥시펜티스터리룬시칸티트런컷9-단순화								2721600	604800
247		t_{0,1,2,3,4,5,7}{3,3,3,3,3,3,3,3,3,3} 헵티펜티스테룬시칸티트런 9-단순화								4989600	907200
248		t_{0,1,2,3,4,6,7}{3,3,3,3,3,3,3,3,3,3} 헵티헥시스터런시칸티트런 9-단순								4536000	907200
249		t_{0,1,2,3,5,6,7}{3,3,3,3,3,3,3,3,3,3} 헵티헥시펜티룬시칸티트런 9-단순화								4536000	907200
250		t_{0,1,2,4,5,6,7}{3,3,3,3,3,3,3,3,3,3} 헵티헥시펜티시스테리칸티트런치 9단순								4536000	907200
251		t_{0,1,3,4,5,6,7}{3,3,3,3,3,3,3,3,3,3} 헵티헥시펜티리스테룬시트루나카미9-단순								4536000	907200
252		t_{0,2,3,4,5,6,7}{3,3,3,3,3,3,3,3,3,3} 헵티헥시펜티리스테룬시칸텔화9-단순화								4536000	907200
253		t_{1,2,3,4,5,6,7}{3,3,3,3,3,3,3,3,3,3} Bihexipentisteriruncicantitruncated 9-simplex								4082400	907200
254		t_{0,1,2,3,4,5,8}{3,3,3,3,3,3,3,3,3,3} 옥티펜티스터라이런시칸티트런컷 9-단순								3326400	604800
255		t_{0,1,2,3,4,6,8}{3,3,3,3,3,3,3,3,3,3} Octihexisteriruncicantitruncated 9-simplex								5443200	907200
256		t_{0,1,2,3,5,6,8}{3,3,3,3,3,3,3,3,3,3} Octihexipentiruncicantitruncated 9-simplex								4989600	907200
257		t_{0,1,2,4,5,6,8}{3,3,3,3,3,3,3,3,3,3} 옥티헥시스테리칸티클라우티드9-단순화								4989600	907200
258		t_{0,1,3,4,5,6,8}{3,3,3,3,3,3,3,3,3,3} 옥티헥시펜티리스테룬시트라우닝 9-단순								4989600	907200
259		t_{0,2,3,4,5,6,8}{3,3,3,3,3,3,3,3,3,3} 옥티헥시펜티스테룬시칸텔화9-단순화								4989600	907200
260		t_{0,1,2,3,4,7,8}{3,3,3,3,3,3,3,3,3,3} 옥티프리스테리룬시칸티트런치드9-단순화								3326400	604800
261		t_{0,1,2,3,5,7,8}{3,3,3,3,3,3,3,3,3,3} 옥티펩티펜티룬시칸티트런 9-단순화								5443200	907200
262		t_{0,1,2,4,5,7,8}{3,3,3,3,3,3,3,3,3,3} 옥티펩티스테리칸티크루티드9-단순화								4989600	907200
263		t_{0,1,3,4,5,7,8}{3,3,3,3,3,3,3,3,3,3} 옥티프티펜티리스테룬시트라우닝 9-단순화								4989600	907200
264		t_{0,1,2,3,6,7,8}{3,3,3,3,3,3,3,3,3,3} 옥티펩티헥시룬시칸트런치 9-단순화								3326400	604800
265		t_{0,1,2,4,6,7,8}{3,3,3,3,3,3,3,3,3,3} 옥티펩티헥시스테리칸티트런치9-단순화								5443200	907200
266		t_{0,1,2,3,4,5,6,7}{3,3,3,3,3,3,3,3,3,3} 헵티헥시펜티리스테룬시칸티트런컷9-단순화								8164800	1814400
267		t_{0,1,2,3,4,5,6,8}{3,3,3,3,3,3,3,3,3,3} Octihexipentisteriruncicantruncated 9-단순화								9072000	1814400
268		t_{0,1,2,3,4,5,7,8}{3,3,3,3,3,3,3,3,3,3} 옥티프티펜티리스테룬시칸티트란치 9-단순화								9072000	1814400
269		t_{0,1,2,3,4,6,7,8}{3,3,3,3,3,3,3,3,3,3} 옥티펩티헥시스테룬시칸티칸트런컷9-단순화								9072000	1814400
270		t_{0,1,2,3,5,6,7,8}{3,3,3,3,3,3,3,3,3,3} 옥티펩티헥시펜티룬시칸트런컷 9-단순화								9072000	1814400
271		t_{0,1,2,3,4,5,6,7,8}{3,3,3,3,3,3,3,3,3,3} 옴니트런치 9-심플렉스								16329600	3628800

B가족₉

하나 이상의 고리가 있는 콕서터-다인킨 다이어그램의 모든 순열을 기반으로 511개의 형식이 있습니다.

11가지 사례를 다음에 나타냅니다.9개의 교정된 형태와 2개의 절단.Bowers 스타일의 머리글자 이름은 상호 참조를 위해 괄호로 둘러싸여 있습니다.Bowers 스타일의 머리글자 이름은 상호 참조를 위해 괄호로 둘러싸여 있습니다.

#	그래프	콕서터-딘킨 도표 슐레플리 기호 이름.	요소수
#	그래프	콕서터-딘킨 도표 슐레플리 기호 이름.	8면	7면	6면	5면	4면	셀	얼굴	가장자리	꼭지점
1		t₀{4,3,3,3,3,3,3,3,3} 9 큐브(enne)	18	144	672	2016	4032	5376	4608	2304	512
2		t_0,1{4,3,3,3,3,3,3,3,3} 잘린 9 큐브(10)								2304	4608
3		t₁{4,3,3,3,3,3,3,3,3} 정류된 9 큐브(렌)								18432	2304
4		t₂{4,3,3,3,3,3,3,3,3} 양방향 9 큐브(barn)								64512	4608
5		t₃{4,3,3,3,3,3,3,3,3} Triregated 9-cube (tarn)								96768	5376
6		t₄{4,3,3,3,3,3,3,3,3} 4등분된 9큐브(nav) (4등분된 9등분)								80640	4032
7		t₃{3,3,3,3,3,3,3,4} 3정류된 9정압(tarv)								40320	2016
8		t₂{3,3,3,3,3,3,3,4} 쌍방향 9정압선(브레이브)								12096	672
9		t₁{3,3,3,3,3,3,3,4} 수정 완료 9-ORTOPLEX(리뷰트)								2016	144
10		t_0,1{3,3,3,3,3,3,3,4} 잘라낸 9개의 직각(tiv)								2160	288
11		t₀{3,3,3,3,3,3,3,4} 9 - ORTOPLEX (VE)	512	2304	4608	5376	4032	2016	672	144	18

D₉ 패밀리

D₉ 제품군의 대칭 차수는 92,897,280(9⁸ 요인 × 2)입니다.

이 계열은 D 콕서터-다인킨 다이어그램의₉ 하나 이상의 노드를 표시하여 생성된 3×128-1=383 와이토피아 균일한 폴리토페를 가진다.이 중 255(2×128-1)는 B 패밀리에서₉ 반복되며 128은 이 패밀리에서 고유하며, 8개의 1 또는 2개의 링형 형식이 아래에 나열되어 있습니다.Bowers 스타일의 머리글자 이름은 상호 참조를 위해 괄호로 둘러싸여 있습니다.

#	콕서터 평면 그래프											콕서터-딘킨 도표 슐레플리 기호	기준점 (대체 서명)	요소수									서클라드
#	B₉.	D₉.	D₈.	D₇.	D₆.	D₅.	D₄.	D₃.	A₇.	A₅.	A₃.	콕서터-딘킨 도표 슐레플리 기호	기준점 (대체 서명)	8	7	6	5	4	3	2	1	0	서클라드
1												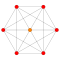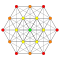9-데미큐브(헨)	(1,1,1,1,1,1,1,1,1)	274	2448	9888	23520	36288	37632	21404	4608	256	1.0606601
2								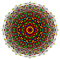				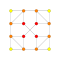잘린 9-데미큐브(thene)	(1,1,3,3,3,3,3,3,3)								69120	9216	2.8504384
3								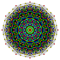				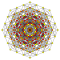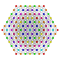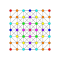캔텔레이트된 9-데미큐브	(1,1,1,3,3,3,3,3,3)								225792	21504	2.6692696
4		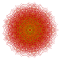										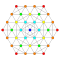룬케이티드9-데미큐브	(1,1,1,1,3,3,3,3,3)								419328	32256	2.4748735
5												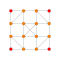입체화 9-데미큐브	(1,1,1,1,1,3,3,3,3)								483840	32256	2.2638462
6												펜텔라티드 9-데미큐브	(1,1,1,1,1,1,3,3,3)								354816	21504	2.0310094
7												헥시드 9-데미큐브	(1,1,1,1,1,1,1,3,3)								161280	9216	1.7677668
8								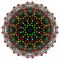				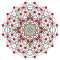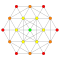헵텔식 9단 반구	(1,1,1,1,1,1,1,1,3)								41472	2304	1.4577379

규칙적이고 균일한 벌집

Coxeter-Dynkin 다이어그램은 패밀리 간의 대응성과 다이어그램 내의 높은 대칭성입니다.각 행의 동일한 색상의 노드가 동일한 미러를 나타냅니다.검은색 노드는 통신에서 활성화되지 않습니다.

8공간에서 규칙적이고 균일한 테셀레이션을 생성하는 5가지 기본 아핀 콕서터 그룹이 있다.

#	콕서터군		폼
1	$(\displaystyle {A}}_{8})$	[3^[9]]	45
2	$(\displaystyle {C}}_{8})$	[4,3⁶,4]	271
3	$(\displaystyle {B}}_{8})$	h[4,3⁶,4] [4,3⁵,3^1,1]	383 (128 신규)
4	$(\displaystyle {D}}_{8})$	q[4,3⁶,4] [3^1,1,3⁴,3^1,1]	155 (15 신규)
5	$(\displaystyle {E}}_{8})$	[3^5,2,1]	511

규칙적이고 균일한 테셀레이션에는 다음이 포함됩니다.

${\tilde {A}}_{8}$ ~ $($ 스타일 ${A}_$ 45개의 고유 링 형식
- 840x 벌집: {3^[9]}
${\tilde {C}}_{8}$ ~ ${\tilde {C}}_{8}$ ({ $displaystyle { C$ }} $_{8})$ 271 ${\tilde {C}}_{8}$ 고유 호출음 형식
- 일반 8큐브 벌집: {4,3⁶,4}
${\tilde {B}}_{8}$ 8 $({$ 383개의 고유 호출음 형식, ${\tilde {C}}_{8}$ ~8({ $displaystyle {C}}_{8$ 128 신규
- 8-데미큐브 벌집: h{4,3⁶,4} 또는 {3^1,1,4⁵} 또는
${\tilde {D}}_{8}$ D ${\tilde {D}}_{8}$ ~ $({$ [3^1,1,3⁴,3^1,1]): 155개의 고유한 링 배열, 그리고 15개는 Q{4,3⁶,4} 또는 q₉†로 표현되는 쿼터 8 큐빅 허니콤이라고 불리는 새로운 ${\tilde {D}}_{8}$ 입니다.
${\tilde {E}}_{8}$ ~ 8 $($ 스타일 ${E}_{8})$ 511 ${\tilde {E}}_{8}$ 폼
- 5₂₁ 벌집:
- 2₅₁ 벌집:
- 벌집₅₂ 1개:

규칙적이고 균일한 쌍곡선 벌집

랭크 9의 콤팩트 쌍곡선 콕서터 군, 모든 유한 패싯을 가진 허니콤을 생성할 수 있는 군 및 유한 정점 도형이 없습니다.단, 등급 9의 4개의 비콤팩트 쌍곡선 콕서터 그룹이 있으며, 각 그룹은 콕서터 다이어그램의 링 순열로 8개의 공간에서 균일한 벌집을 생성한다.

${\bar {P}}_{8}$ ${\bar {P}}_{8}$ $($ 스타일 {P $}}_{8})$ = ${\bar {P}}_{8}$ [3^[8],3]:	${\bar {Q}}_{8}$ ${\bar {Q}}_{8}$ $($ 스타일 ${Q}_{8})$ = ${\bar {Q}}_{8}$ [3^1,1,3³,3^2,1]:	${\bar {S}}_{8}$ ${\bar {S}}_{8}$ $($ 스타일 ${S}_{8})$ = ${\bar {S}}_{8}$ [4,3⁴,3^2,1]:	${\bar {T}}_{8}$ ${\bar {T}}_{8}$ $($ 스타일 {T} $_{8})$ = ${\bar {T}}_{8}$ [3^4,3,1]:

레퍼런스

^ ^a ^b ^c 루손, D.; 오일러의 보석: 다면체 공식과 토포로지 탄생, 프린스턴, 2008.

T. 고셋:N차원 공간의 정칙 및 반정규 도형에 대하여, 맥밀런, 1900
A. Boul Stott: 정규 폴리토프와 공간 채우기에서 반규칙의 기하학적 차감, Koninklijke Academy van Wetenschappen 폭 단위 Amsterdam, Eerste Sepie 11, 1, Amsterdam, 1910년
H.S.M. 콕서터:
- H.S.M. Coxeter, M.S. Longuet-Higgins und J.C.P. Miller:Uniform Polychedra, Londne, 1954년 런던 왕립학회 철학거래
- H.S.M. Coxeter, Regular Polytopes, 제3판, 도버 뉴욕, 1973년
만화경: H.S.M. 콕서터 선정필, F. 편집자 F.S.M. 콕서터.아서 셔크, 피터 맥멀런, 앤서니 CThompson, Asia Ivic Weiss, Wiley-Intercience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (페이퍼 22) H.S.M. 콕서터, 정규 및 준정규 폴리토피스 I, [수학]Zeit.46 (1940) 380 ~ 407, MR 2,10]
- (페이퍼 23) H.S.M. 콕서터, 정규 및 반정규 폴리토피스 II, [수학]Zeit. 188 (1985) 559-591]
- (문서 24) H.S.M. 콕서터, 정규 및 반정규 폴리토피스 III, [수학]Zeit. 200 (1988) 3-45]
N.W. 존슨:균일한 폴리토피와 허니콤의 이론,1966년 토론토 대학교 논문
Klitzing, Richard. "9D uniform polytopes (polyyotta)".

외부 링크

폴리토프 이름
다양한 차원의 폴리토퍼스, 조나단 바우어스
다차원 용어집
하이퍼 스페이스 용어집, 조지 올셰프스키

v t 치수 2-10의 기본 볼록 정규 및 균일한 폴리토프
가족	A_n	B_n	I₂(p) / D_n	E₆/E₇/E₈/F₄/G₂	H_n
정다각형	삼각형	광장	p곤	육각형	펜타곤
균일한 다면체	사면체	8면체 • 큐브	데미큐브		12면체 • 이십면체
균일한 폴리코론	펜타코론	16 셀 • 테서랙트	데모테서랙트	24 셀	120 셀 • 600 셀
균일한 5 폴리토프	51200x	5 - ORTOPLEX • 5 - 큐브	5 데미큐브
균일한 6 폴리토프	61200x	6-정류 • 6-큐브	6-데미큐브	1₂₂ • 2₂₁
균일한 7 폴리토프	71200x	7-정류 • 7-큐브	7 데미큐브	1₃₂ • 2₃₁ • 3₂₁
균일한 8 폴리토프	8180x	8-정류 • 8-큐브	8개의 데미큐브	1₄₂ • 2₄₁ • 4₂₁
균일한 9-폴리토프	9169x	9-정류 • 9-입방체	9데미큐브
균일한 10 폴리토프	10-1996x	10 - ORTOPLEX • 10 - 큐브	10 데미큐브
균일한 n-폴리토프	n-1996x	n-ortoplex • n-입방체	n-데미큐브	1_k2 • 2_k1 • k₂₁	n-오각형 폴리토프
주제: 폴리토프 패밀리 • 일반 폴리토프 • 일반 폴리토프 및 화합물 목록

v t 치수 2-9의 기본 볼록 규칙적이고 균일한 벌집
공간	가족	$({displaystyle {A}}_{n-1})$	$({displaystyle {C}}_{n-1})$	$(\displaystyle {B}}_{n-1})$	$({displaystyle {D}}_{n-1})$	$($ 스타일 ${G}_{2})$ / $($ 스타일 { $F}_{4})$ / $($ 스타일 ${E}_{n-1})$
E².	균일한 타일링	{3^[3]}	δ₃	할₃ 수 있다	문제₃	육각형
E³.	균일한 볼록한 벌집	{3^[4]}	δ₄	할₄ 수 있다	문제₄
E⁴.	균일한 4-허니콤	{3^[5]}	δ₅	할₅ 수 있다	문제₅	24셀 벌집
E⁵.	균일한 5벌집	{3^[6]}	δ₆	할₆ 수 있다	문제₆
E⁶.	균일한 6벌집	{3^[7]}	δ₇	할₇ 수 있다	문제₇	2개₂₂
E⁷.	균일한 7벌집	{3^[8]}	δ₈	할₈ 수 있다	문제₈	1₃₃ • 3₃₁
E⁸.	균일한 8벌집	{3^[9]}	δ₉	할₉ 수 있다	문제₉	1₅₂ • 2₅₁ • 5₂₁
E⁹.	균일한 9벌집	{3^[10]}	δ₁₀	할₁₀ 수 있다	문제₁₀
E¹⁰.	균일한 10벌집	{3^[11]}	δ₁₁	할₁₁ 수 있다	문제₁₁
E^n-1.	균일한 (n-1)-벌집	{3^[n]}	δ_n	할_n 수 있다	문제_n	1_k2 • 2_k1 • k₂₁

[richeson-1] 루손, D.; 오일러의 보석: 다면체 공식과 토포로지 탄생, 프린스턴, 2008.

[1]

Search

균일한 9-폴리토프

네임스페이스

더

목차

표준 9-폴리토프

오일러 특성

기본 콕서터군별 균일한 9-폴리토피스

A가족₉

B가족₉

D₉ 패밀리

규칙적이고 균일한 벌집

규칙적이고 균일한 쌍곡선 벌집

레퍼런스

외부 링크


9169x						수정 완료 9-심플렉스
잘라낸 9-심플렉스						9개의 심플렉스(cantellated
Runcated 9 심플렉스						입체화 9-심플렉스
펜텔레이티드 9-심플렉스						9단독화
헵텔레이트 9-단형						옥텔레이티드 9-단순
9직교						9큐브
잘린 9직선						잘린 9 큐브
수정 완료 9-ORTOPLEX						정류된 9-큐브
9데미큐브						잘려나간 9단기

Search

균일한 9-폴리토프

표준 9-폴리토프

오일러 특성

기본 콕서터군별 균일한 9-폴리토피스

A가족9

B가족9

D9 패밀리

규칙적이고 균일한 벌집

규칙적이고 균일한 쌍곡선 벌집

레퍼런스

외부 링크

A가족₉

B가족₉

D₉ 패밀리