데카르트 정리

기하학에서 데카르트 정리는 네 개의 키스 또는 서로 접선하는 원에 대해 원의 반지름이 특정 2차 방정식을 만족한다는 것을 말합니다.이 방정식을 풀면 주어진 세 개의 서로 접선하는 네 번째 원을 만들 수 있습니다.이 정리는 1643년 르네 데카르트의 이름을 따서 지어졌습니다.

프레데릭 소디(Frederick Soddy)의 1936년 시 키스 정밀(The Kiss Precision)은 이 정리를 네 원의 굴곡(역반지름)으로 요약합니다.

4개의 모든 곡선의 합
그들의^[1] 반은 그들의 금액의 제곱입니다.

이 정리의 특수한 경우는 원 중 하나 또는 두 개가 직선으로 바뀌었을 때(곡면이 0인 경우) 또는 곡선이 정수 또는 제곱수일 때 적용됩니다.복소수를 사용하는 정리의 버전은 원의 반지름뿐만 아니라 중심을 계산할 수 있게 합니다.적절한 곡률 정의를 사용하면 구면 기하학 및 쌍곡 기하학에서도 이 정리가 적용됩니다.고차원에서 유사한 2차 방정식은 쌍방향 접선 구 또는 초구 시스템에 적용됩니다.

역사

접선원과 관련된 기하학적인 문제들은 수 천년 동안 숙고되어 왔습니다.기원전 3세기의 고대 그리스에서, 페르가의 아폴로니오스는 이 주제에 대한 책 전체를 바쳤습니다.그것은 소실되었고, 주로 알렉산드리아의 파푸스에 의해 그것의 내용에 대한 설명과 중세 이슬람 ^[2]수학에서 그것에 대한 단편적인 언급을 통해 알려져 있습니다.하지만, 그리스 기하학은 주로 직선과 나침반 구조에 집중되어 있었습니다.예를 들어, 데카르트의 정리와 밀접하게 관련된 아폴로니우스의 문제는 세 개의 주어진 원에 접하는 원의 구성을 요구하는데, 이 원들은 그들 자신이 ^[3]접할 필요가 없습니다.대신, 데카르트의 정리는 기하학적 형태를 설명하는 수들 사이의 대수적 관계를 사용하여 공식화됩니다.이것은 17세기 ^[4]전반에 르네 데카르트와 피에르 드 페르마가 개척한 분야인 분석 기하학의 특징입니다.

데카르트는 1643년 팔츠의 ^[5]엘리자베스 공주에게 보낸 두 통의 편지에서 접선원 문제에 대해 간단히 논의했습니다.데카르트는 처음에 아폴로니우스의 문제를 공주에게 제기했습니다.엘리자베스의 부분적인 결과들이 전체 문제를 해석적으로 푸는 것이 너무 지루할 것이라는 것을 알게 된 후, 그는 문제를 주어진 세 개의 원이 서로 접하는 경우로 단순화시켰고, 이 단순화된 문제를 푸는 과정에서 그는 반지름들 사이의 관계, 즉 곡률들을 묘사하는 방정식을 생각해 냈습니다.4개의 쌍방향 접선원의.이 결과는 데카르트의 ^[6][7]정리로 알려지게 되었습니다.불행하게도 데카르트가 이 관계를 발견한 이유는 ^[8]사라졌습니다.

1751년 일본 수학자 누시즈미 야마지가 데카르트의 원 정리의 한 형태를 언급하면서, 일본 수학자들은 원과 ^[9]그 접선에 관한 문제를 자주 다루었습니다.데카르트처럼, 그는 그것을 곡률이 ^[10][11]아닌 반지름에 대한 다항식으로 표현했습니다.이 정리의 특수한 경우는 1824년부터 ^[12]일본의 상가쿠 석판에 기록되어 있습니다.

데카르트의 정리는 1826년 야코프 ^[13]슈타이너에 의해, 1842년 필립 ^[14]비크로프트에 의해, 1936년 프레드릭 소디에 의해 재발견되었습니다.Soddy는 그의 정리의 형식을 시 "The Kiss Precise"로 정했고, 그것을 Nature에 출판했습니다.이 문제의 키스 서클은 때때로 소디 서클로 알려져 있습니다.소디는 또한 이 정리를 ^[1]구들로 확장했고, 또 다른 시에서 각각 이웃에 접하는 6개의 구들과 현재 소디의 [15]육각형이라고 불리는 3개의 주어진 상호 접선 구들의 사슬을 묘사했습니다.소롤드 고셋은 그 정리와 시를 임의의 ^[16]차원으로 확장시켰습니다.일반화는 때때로 소디-고셋 ^[17]정리라고 불리기도 하지만, 육각형과 3차원 버전 모두 일찍이 Sangaku와 Robert Lachlan의 ^[12][18][19]1886년 연구에서 알려져 있습니다.

파푸스 사슬의 원의 높이를 묻는 데카르트 정리와 관련된 문제는 소련에서 유대인들을 모스크바 주립대학 수학 ^[20]프로그램에서 제외시키기 위해 구술 시험에 사용된 많은 "킬러" 문제 중 하나였습니다.

그 정리의 여러 가지 증명들이 출판되었습니다.슈타이너의 증명은 파푸스 사슬과 비비아니의 정리를 사용합니다.필립 비크로프트와 H. S. M. 콕서터의 증명은 원래 세 원의 접선의 세 배를 통과하는 네 개의 원을 더 포함합니다. 콕서터는 또한 역기하학을 사용하여 증명을 제공했습니다.추가적인 증명에는 대칭성에 기초한 논쟁, 외부 대수학에서의 ^[21][22]계산 또는 헤론 공식의 대수적 조작이 포함됩니다.

진술

데카르트의 정리는 원의 ^[23]곡률로 가장 쉽게 표현됩니다.원의 부호 있는 곡률(또는 굽힘)은 k = ± ${\displaystyle 1}$/ ${\displaystyle r}${\$displaystyle$ k =\$pm$ 1$/r$로 정의되며, $여기$서 r$${\$displaystyle$ r$}$은(는) 원의 반지름입니다.원이 클수록 곡률의 크기가 작으며, 그 반대의 경우도 마찬가지입니다.k = ± ${\displaystyle 1}$/ ${\displaystyle r}$ ${\displaystyle$ k =\$pm$ 1$/r}$ 기호$(±$ ${\displaystyle$ \$pm$ 기호로 표시)는 다른 원과 외부적으로 접하는 원에 대해 양수입니다.다른 원을 둘러싸는 커다란 빨간색 원과 같은 내부 접선 원의 경우 부호가 음수입니다.직선이 곡률이 0인 축퇴 원으로 간주되면 데카르트 정리는 선과 세 개의 서로 접선하는 원에도 적용됩니다(일반화 ^[1]원 참조).

i = ${\displaystyle 1,}$ ${\displaystyle \dots ,}$ 4$${\$displaystyle$ i = $1,\n2,4$에 $대해$ $곡률$ ${\displaystyle {키}_{}}${\$displaystyle k_{i}}$을 갖는 6개의 서로 다른 점에서 서로 접하는 4개의 원에 대해 데카르트 정리는 다음과 같이 말합니다.

네 개의 곡률 중 하나가 변수이고 나머지가 상수라고 간주되면 이는 2차 방정식입니다.3개의 주어진 키싱 원에 접하는 네 번째 원의 반지름을 구하기 위해, 2차 방정식은 다음과^[13][24] 같이 풀 수 있습니다.

$\pm {\displaystyle }$ ${\displaystyle \pm}$ 기호는$$ 일반적으로 이 방정식에 두 개의 해가 있고 접선원의 세 배는 두 개의 접선원(또는 축퇴 직선)이 있음을 나타냅니다.문제별 기준은 주어진 ^[21]문제에서 이 두 솔루션 중 하나를 다른 솔루션보다 선호할 수 있습니다.

이 정리는 동일한 점에서 두 개 이상의 원이 서로 접하는 원 시스템에는 적용되지 않습니다.접선점이 ^[8]구별되어야 합니다.한 점에서 두 개 이상의 원이 접하면 임의의 곡률을 가진 원이 무한히 많이 있을 수 있습니다. ^[25]원의 연필을 참조하십시오.

원 중심 위치 찾기

원을 완전히 결정하려면 원의 반지름(또는 곡률)뿐만 아니라 원의 중심도 알아야 합니다.데카르트 좌표$({\displaystyle x,y}$)$${\$displaystyle(x,y)}$을(를) ${\displaystyle \mathrm{복소수}}$ z${\displaystyle }$= x + i {\$displaystyle$ z =$x$ + $iy$로 해석하면 관련 방정식이 가장 명확하게 표현됩니다.그 다음 방정식은 데카르트의 정리와 비슷해 보이고 따라서 복잡한 데카르트 정리라고 불립니다.i ∈ {${\displaystyle 1,}$ ${\displaystyle 2,}$ ${\displaystyle 3,}$ ${\displaystyle 4\}}$ ${\displaystyle$ i$\in \{1, 2, 3, 4$에 대해 $곡률$ ${\displaystyle {키}_{}}${\$displaystyle k_{i$}와 $중심$ ${\displaystyle {zi}_{}}${\$displaystyle z_{i}$가 있는 네 개의 원이 주어지면 식 (1) 외에 다음과 같은 동등함이 성립합니다.

식 (2)를 사용하여 ${\displaystyle {k\mathrm{}}_{}}$ 4 ${\$가 $발견$되면 식 (3)을 2차 방정식으로 풀어 z 4$${\$displaystyle z_{4}}$를 $계산$하고 식 (2)와 유사한 형태로 이어집니다.

다시 말하지만, 일반적으로 ${\displaystyle {k4\mathrm{}}_{}}${\$displaystyle k_{4$에 대한 두 솔루션에 ${\displaystyle {대응}_{}}$하는$$z4 {\$displaystyle z_{$4$$}}에 대한 두 솔루션이 있습니다.${\displaystyle {z4\mathrm{}}_{}}$ ${\$의 위 수식에서 플러스/마이너스 기호가 ${\displaystyle {k4\mathrm{}}_{}}$ ${\$^[17][26][27]의 수식에서 플러스/마이너스 기호와 반드시 일치하는 것은 아닙니다.

특수한 경우

합동원 3개

네 개의 원들 중 세 개가 합동일 때, 그들의 중심은 그들의 접선점들처럼 정삼각형을 형성합니다.세 개 모두에 접하는 네 번째 원에 대한 두 가지 가능성은 동심원이며, 식 (2)는 다음과 같이 감소합니다^[28].

하나 이상의 직선

세 개의 원 중 하나가 나머지 원과 접하는 직선으로 바뀌면 곡률은 0이고 식 (1)에서 탈락합니다.예를 들어, k ${\displaystyle 3_{}}$ = ${\displaystyle 0}${\$displaystyle k_{3$}=$0$인 $경우$, 식 (1)을 다음과 같이 인수분해할 수 있습니다.

식 (2)는 다음과 같이 단순화됩니다^[30].

양변의 제곱근을 취하면 이 경우의 다른 대체 공식이 됩니다(${\displaystyle {k\mathrm{}}_{}}$ 1 ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}${\$displaystyle k_{1}\geq k_{2$}}).$$

이것은 "피타고라스 ^[23]정리의 일종의 훼손된 버전"으로 묘사되어 왔습니다.

두 개의 원이 선으로 교체된 경우 교체된 두 원 사이의 접선이 두 교체 선 사이의 평행선이 됩니다.이 경우, ${\displaystyle k_{}}$ 2 = ${\displaystyle k_{}}$ 3 = ${\displaystyle 0}${\$displaystyle k_{2$} =$k_{3$} = $0$일 때, 식 (2)는 사소한 것으로 줄어듭니다.

이는 네 개의 곡선이 모두 상호 접선 상태를 유지하려면 다른 두 원이 ^[17][24]합동이어야 한다는 관측치에 해당합니다.

정수곡률

식 (2)에 의해 기술된 4개의 접선 원이 모두 정수 곡률을 가질 때, 식의 두 번째 해에 의해 기술된 대체 4번째 원도 정수 곡률을 가져야 합니다.이것은 두 해 모두 정수와 정수의 제곱근이 다르기 때문에, 이 제곱근이 정수일 경우에만 어느 해도 정수가 될 수 있고, 따라서 다른 해도 정수가 될 수 있기 때문입니다.데카르트 정리에서 방정식을 만족하는 정수 4개마다 4개의 ^[31]접선원의 곡률을 형성합니다.이 유형의 정수 4배는 변과 넓이가 정수인 헤로니아 삼각형,^[32] 삼각형과도 밀접한 관련이 있습니다.

임의의 4개의 상호 접선원에서 시작하여, 모든 가능한 방법으로 4개 중 하나를 대체해(비에타 점프) 반복적으로 대체하면 아폴론 개스킷이라고 불리는 무한히 많은 접선원의 시스템으로 이어집니다.처음 네 개의 원이 정수 곡률을 가지면 교체마다 마찬가지이며 따라서 개스킷의 모든 원이 정수 곡률을 갖습니다.정수 곡률을 갖는 임의의 4개의 접선원은 가장 큰 4개의 원과 가장 작은 4개의 곡률을 갖는 근 4중주로 유일하게 설명되는 개스킷에 속합니다.이 4중 원은 동일한 개스킷의 다른 4중 원에서 시작하여, 가장 작은 원을 동일한 데카르트 방정식을 푸는 더 큰 원으로 반복적으로 교체하여 그러한 감소가 ^[31]불가능할 때까지 찾을 수 있습니다.

근 4중주는 중요하지 않은 공약수를 가지지 않는다면 원시적이라고 합니다.모든 원시 근 4중항은 두${\displaystyle {}^{}{}^{}}$의 ${\displaystyle {합}^{}}$ n $2{\displaystyle {}^{}}$+ ${\displaystyle m}$2 = $de$ {\$displaystyle$n^{2} + m$^{2$}에서 찾을 수 있습니다.}$=$$de$$\}:$ 4중 ${\displaystyle (-n,d}$ + ${\displaystyle n,e}$ + ${\displaystyle n,d}$ +${\displaystyle e}$ +${\displaystyle n}$ - $)$ {\$displaystyle$ (-${\displaystyle n}$$,\, d$ + $n,\, e$ + $n,\, d + e$ + n - $2m$ 프리미티브가 되려면 추가 조건${\displaystyle gcd}$ ($,$ d${\displaystyle ,}$ ${\displaystyle e}$ )${\displaystyle }$$=$ 1 ${\displaystyle$ \$gcd(n, d, e)$$=$ 1$\},$ - ${\displaystyle n}{\displaystyle \le }$ ${\displaystyle 0}$≤ 2 m ${\displaystyle \le }$ ${\displaystyle d}$ $≤$e {\$displaystyle -n\leq 0\leq 2m\leq$ d$\$leq e$\}$를 만족해야 합니다$.$두 제곱의 합 인수분해는 두 제곱의 합 정리를 사용하여 구할 수 있습니다.임의의 다른 정수 아폴론 개스킷은 원시 루트 4중체에 임의의 정수를 곱하여 형성할 수 있으며, 이러한 개스킷 중 하나의 4중체(즉, 데카르트 방정식의 임의의 정수 해)는 루트 4중체를 찾는 데 사용되는 대체 프로세스를 반대로 하여 형성할 수 있습니다.예를 들어, 그림에 표시된 루트$$쿼드러플${\displaystyle (-10,}$ ${\displaystyle 18,}$ ${\displaystyle 23,}$ ${\displaystyle 27)}${\$displaystyle$(-$10, 18, 23, 27$인 개스킷은 두 ${\displaystyle {정사각형}^{}}$ ${\displaystyle {102}^{}}$+ ${\displaystyle {22}^{}}$= ${\displaystyle 8}$ ⋅ ${\displaystyle 13}${\$displaystyle$ 10$^{2}$ + $2^{2$} = $8\cdot$ 13$\}$의 인수합에서 이러한 방식으로 생성됩니다.

포드 서클

하나의 직선과 정수 곡선의 특수한 경우가 포드 원 안에서 결합됩니다.이들은 직각좌표계의 x {\$displaystyle$ x$$$}$ $축$에 접하는 무한 원군이며, 이들은 그 유리한 점에서 직각좌표계의 x ${\displaystyle$ x} 축에 접합니다.각 $분수{\displaystyle }$ p${\displaystyle /q}$ ${\displaystyle$p/$q}($가장 낮은 용어로)는 점${\displaystyle (p/\mathrm{q}}$,0$)$ {\$displaystyle(p/q,0$)}의$$ 선과 접하는 원으로 $곡률{\displaystyle \mathrm{}}$ ${\displaystyle {2q\mathrm{}}^{}}$ 2${\$를 갖습니다. 이 중 세 개의 곡률은 축의 곡률 0과 함께,두 개의 대응하는 분수의 분모가 세 번째 분모에 합해질 때마다 데카르트 정리의 조건을 만족시킵니다.분수 p / q {\displaystyle p/q} 및 r / s {\displaystyle r/s}(둘 다 가장 낮은 용어)에 대한 두 포드 원은 ps - q r = 1 {\displaystyle ps-qr = 1}일 때 접한다. 접하면 x {\displaystyle x} 축과 중간자 (p + r ) / ( q + s ) {\displaystyle (p)에 접한다$+r)/(q+s$^[33]

포드 원은 루트$$쿼드러플(0, 0, 1$,$ 1${\displaystyle )}${\$displaystyle(0, 0, 1, 1$ x$${\displaystyle x} 축 및 y = ${\displaystyle 1}$ ${\displaystyle$ y =$1$ $선$으로 선택할 수 있는 두 평행선 사이에 경계가 있는 특수 아폴론 개스킷에 속합니다.이 개스킷은 직선을 포함하는 유일한 Apollonian 개스킷이며 음의 곡률을 가진 원 내에 국한되지 않습니다.포드 원은 이 개스킷의 x ${\displaystyle$ x$}$ ^[31]축에 접하는 원입니다.

기하학적 진행

데카르트 정리에서 원의 4개 반지름이 $비율{\displaystyle }$≥ ${\displaystyle$ \$rho$인 기하학적 진행 상태라고 가정할 때, 곡률 또한 동일한 진행 상태에 있습니다.이 비율을 정리에 대입하면 다음과 같은 식을 얻을 수 있습니다.

오직 하나의 실제 해가 1보다 더 큰, 비율을 가지고 있는.

여기서 φ ${\displaystyle \varphi}$는 황금 비율입니다.만약 같은 진행이 양방향으로 계속된다면, 각각의 연속된 네 개의 숫자는 데카르트 정리에 따르는 원들을 묘사합니다.원의 이중 끝 기하학적 진행은 콕서터의 접선원의 복소로믹 시퀀스라고 불리는 접선원의 단일 나선형 패턴으로 배열될 수 있습니다.1968년 ^[34][35]H. S. M. 콕서터에 의해 고차원의 유사한 구조와 함께 처음 기술되었습니다.

삼각형의 구불구불한 원.

평면에 있는 모든 삼각형에는 꼭짓점에 중심을 둔 세 개의 외부 접선 원이 있습니다.A, B, C {\displaystyle A,B,C}를 세 점이라 하고, a, b, c {\displaystyle a,b,c}를 반대변의 길이, s = 12 (a + b + c) {\tfrac {1}{2}}(a + b + c)라고 하면, 이 세 원은 반지름 s - a, s - b, s - c {\displaystyle s-a,s-b,s-c}를 갖는다. 데카르트 정리에 따르면, 두 개의 원이 더 있고, 때로는 두 개의 원이 더 있다Soddy circle이라고 불리는 es는 이 세 원에 접합니다.그것들은 원형과 내부 그리고 ^[36][37][38]외부로 분리되어 있습니다.데카르트 정리를 사용하여 내부 소디 원의 곡률이$$($\mathrm{4R}$+$r$ + $\mathrm{2s})$ / δ ${\$textstyle ($4R + r$ + $2s)/\$임을 나타낼 수 $있습니다.$$델타$ $\}($여기서 $\Delta {\displaystyle \mathrm{}}${\$displaystyle \Delta }$은 삼각형의 면적,$$R {\$displaystyle$R}은$$(는) 그 원반지름, $r{\displaystyle }$ ${\displaystyle$ r$}$은(는) 그 반지름입니다.바깥쪽 소디 원의$$곡률은 ($\mathrm{4R}$ $+r$ - $\mathrm{2s})$ / δ ${\textstyle (4R$+ r - 2s) /\$Delta$ $\}$이며, 안쪽 곡률은 항상 양수이지만 바깥쪽 곡률은 양수, 음수, 0일 수 있습니다.바깥쪽 원이 곡률이 0인 직선으로 퇴화하는 삼각형은 "소디안 삼각형"^[39]이라고 불립니다.

데카르트 정리의 많은 증명들 중 하나는 삼각형 기하학과의 연관성과 삼각형의 변의 길이에 대한 헤론의 넓이에 대한 헤론의 공식에 근거한 것입니다.반지름이 1, r2, r3, {\displaystyle r_{1}, r_{2}, r_{3}인 세 개의 원이 외부에서 접하면 중심 P1, P2, P3 {\displaystyle P_{1}, P_{2}, P_{3}}는 변의 길이가 r1 + r2인 삼각형의 꼭짓점을 이룬다. {\displaystyle r_{1} + r_{2}, r1 + r_{2}, r3, {\displaystyle r_{1} + r_{3}, r2 + r3, {\displaystyle r_{2} + r_{3}$,}$그리고 $반지름$ ${\displaystyle r_{}}$ 1${\displaystyle {}_{}}$+ ${\displaystyle 2_{}}$ + ${\displaystyle r_{}}$ 3${\displaystyle {}_{}}${\$displaystyle r_{1}$ + $r_{2}$ + $r_{3}}$ 헤론의 공식에 의해, 이 삼각형 $△$ ${\displaystyle P_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle P_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle P_{}}$3 {\$displaystyle$\displaystyle \$displayp_{1}P_{2}P_{3}}$의 넓이를 갖습니다.

이제 삼각형 내부의 $점{\displaystyle {}_{}}$ ${\displaystyle {P\mathrm{}}_{}}$ 4$${\$displaystyle P_{4}}$에 $반지름{\displaystyle {}_{}}$ ${\displaystyle {r\mathrm{}}_{}}$ 4${\displaystyle {}_{}}$ ${\displaystyle r_{4}}$이 있는 내부 소디 원을 생각해 보십시오.삼각형 △ P 1 P 2 P 3 {\displaystyle \displaystyle \display_{1}P_{2}P_{3}}개의 더 작은 삼각형 △ P 1 P 2 P 4, {\displaystyle \displaytyle \displayp_{1}P_{2}P_{4}P_{4}P_{3}, △ P 1 P 4 P 3, {\displaystyle \displayp_{1}P_{4}P_{3},$}$${\displaystyle {R4\mathrm{}}_{}}$ ${\$을(를) 위의 면적 공식에서 다른 반지름 중 하나로 $대체$하여 얻을 수 있는$$ 면적.첫 번째 삼각형의 면적은 다음 세 영역의 합과 같습니다.

세심한 대수적 조작은 이 공식이 데카르트의 ^[21]정리인 식 (1)과 동등하다는 것을 보여줍니다.

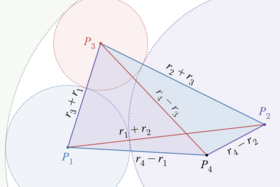
이 분석에서는 네 개의 원이 외부에서 접하게 되는 모든 경우를 다룹니다. 하나는 항상 다른 세 개의 원의 내부 소디 원입니다.원들 중 하나가 다른 세 개와 내부적으로 접하며 바깥쪽 소디 원을 형성하는 경우도 유사합니다.다시 네 중심 P 1, P 2, P 3, P 4 {\displaystyle P_{1}, P_{2}, P_{3}, P_{4}가 네 개의 삼각형을 이루지만 (P 4 {\displaystyle P_{4}}가 바깥쪽 소디 원의 중심이라고 하자) P 4에 입사하는 삼각형 변 {\displaystyle P_{4}}은 반지름의 차이, r 4 - r 1, {\displaystyle r_{4} - r 1, {\displa$ystyle r_{4}-r_{1},$ ${\displaystyle {r4}_{}}$ - ${\displaystyle {r3\mathrm{}}_{}}$ ${\displaystyle r_{4}-r_{3$$}}.$${\displaystyle {P4\mathrm{}}_{}}$ ${\$ P_${4}}$는 다른 세 중심에 의해 형성된 삼각형의 안쪽 또는 바깥쪽에 놓일 수 ${\displaystyle {\mathrm{있습니다}}_{}}$. 그 삼각형이 안쪽에 있을 때 이 삼각형의 넓이는 위와 같이 다른 세 삼각형의 넓이의 합과 같습니다.바깥에 있을 때, 네 중심에 의해 형성된 사변형은 대각선으로 두 삼각형으로, 두 삼각형 영역의 합과 다른 두 삼각형 영역의 합 사이에 동일성을 부여할 수 있습니다.모든 경우에 면적 방정식은 데카르트 정리로 줄어듭니다.이 방법은 원 중 하나가 선으로 퇴화되는 경우에는 직접 적용되지 않지만 ^[21]원의 제한적인 경우로 처리할 수 있습니다.

일반화

임의의 4원 구성

데카르트의 정리는 행렬 방정식으로 표현된 다음 행렬을 변경하여 4개의 방향 원으로 구성된 다른 형태로 일반화할 수 있습니다.k ${\$을(를) 네 원 곡률의 열 벡터라고 $하고{\displaystyle \mathbf{}}$, Q ${\$을(를) 계수 ${\displaystyle {\mathrm{qi},}_{}}$j {\$displaystyle q_{i,$j$$}가 교차점에서 i번째 원과 j번째 원 사이의 상대적인 방향을 나타내는 대칭 행렬이라고 합니다.

그러면 식 (1)을 행렬식으로^[17][40] 다시 쓸 수 있습니다.

데카르트 정리의 일반화로서, 수정된 $대칭행렬{\displaystyle \mathbf{}}$ Q ${\$는 다음과 같이 정의되는 두 원 사이의 $기울기{\displaystyle {}_{}}$ ${\displaystyle {qi,j}_{}}$ ${\$로 각 계수를 대체함으로써 네 원의 원하는 구성을 나타낼 수 있습니다.

$여기$서 ${\displaystyle {}_{}{}_{}}$ ${\displaystyle {rj}_{}}$ ${\$},$r_{j}$는 원의 각각의 반지름이고, ${\displaystyle {di,j}_{}}$ ${\$는 중심 ^[41][42][43]사이의 유클리드 거리입니다.원들이 $교차$할 때,${\displaystyle {\mathrm{qi}}_{}}$, ${\displaystyle j{}_{}}$= cos${\displaystyle }$⁡ ( θ${\displaystyle i_{}}$ j$$) {\$displaystyle q_{i$,j$}$=$\cos$(\$theta _{i,$j$\}\}),$ 원들 사이의 교차각의 코사인.원이 접선점에서 같은 방향으로 향할 때의 기울기는 1 {\displaystyle 1}이고, 두 원이 접선점에서 접선점과 반대 방향으로 향할 때의 기울기는 1 {\displaystyle -1}이고, 직교원의 경우 0 {\displaystyle 0}이며, 간격 [-1, 1] {\dis]입니다$재생$ 스타일 $[-1,1]}$을(를) 선택하고, 하나의 원이 한 ^[40][35]점으로 축퇴함에 따라 제한값 ${\displaystyle \infty}$을$({\displaystyle \mathrm{}}$를) 선택합니다.

${\displaystyle {}^{}}$$$${\displaystyle {\mathrm{k}}^{}}$T - 1 $k$= 0 {\$displaystyle$$\mathbf$ {k}$^{\mathsf {T$$}}\$$mathbf$ {$Q}^{-1}\mathbf$ {k}$$= 0$}$은(는) 평면에 있는 4개 원의 임의 구성에 대해 만족합니다.

구면 및 쌍곡 기하학

데카르트 정리는 j ${\displaystyle$ j$}$ 원의 곡률이 k $j_{}$ = $\cot$ ⁡ $j_{}$ ${\textstyle k_{j$}=\$cot \rho$ _${j},$ 배향된 고유 반지름 ρ j${\displaystyle {}_{}}$ {\$displaystyle \rho$ _${j}$의 공접점인 $경우$ 구면 기하학에서 큰 원 또는 작은 원을 상호 접하게 일반화합니다$.$$}$그러면$$:^[42][17]

곡률 중 하나를 나머지 세 개로 풀어보면

행렬 방정식으로,

$수량$ 1${\displaystyle }$/ ${\displaystyle {kj}_{}}$ = ${\displaystyle \tan }$ ⁡ ${\displaystyle j_{}}${\$displaystyle$ 1 / $k_{j$}=\$tan \rho_{j}}$는 작은 원의 "영문 지름"입니다.원의 어떤 점이 원점에 투영될 때 입체 투영 평면에서 지름의 유클리드 길이입니다.대원의 경우, 이러한 입체 사영은 원점을 통과하는 $직선$이므로, ${\displaystyle {kj}_{}}$ = ${\displaystyle 0}${\$displaystyle k_{j$}=$0$입니다.

마찬가지로, 만약 $j${\$displaystyle$ j$}$번째 사이클의 곡률이 $k_{}$ j = $\coth$ ⁡ $j_{}$ ${\textstyle k_{j$}=\$coth \rho$_{$j},$ 배향된 고유 반지름 ρ${\displaystyle {}_{}}$j의 쌍곡 공접점, {\$displaystyle \rho$ _${j}$로 정의된다면, 이 정리는 쌍곡 기하학에서 상호 접선원으로 일반화됩니다$.$$}$그러면$$:^[17][42]

곡률 중 하나를 나머지 세 개로 풀어보면

행렬 방정식으로,

이 공식은 또한 ${\displaystyle {kj}_{}}${\$displaystyle k_{j}}$를 사이클의 입체 직경의 역수로 할 $경우{\displaystyle {}_{}}$ 하이퍼사이클 및 호로사이클을 포함한 쌍곡 기하학에서 상호 접선 구성을 유지합니다.지름의 한 끝점을 ^[45]원점에 투영할 때 입체 투영(Poincaré 디스크 모델)하는 지름입니다.쌍곡선은 중심이나 고유반지름이 잘 정의되어 있지 않으며, 쌍곡선은 중심과 무한 고유반지름에 이상적인 점을 가지고 있지만, 쌍곡선 원의 경우 kj > 1 {\displaystyle k_{j} > 1, kj = 1 {\displaystyle k_{j} = 1}, 쌍곡선의 경우 kj < 1 {\displaystyle k_{j} < 1},측지선인 경우 ${\displaystyle {kj}_{}}$ = ${\displaystyle 0}${\$displaystyle k_{j$}=$0}$입니다.

고차원

n개의 ${\displaystyle$ n$}$차원 유클리드 공간에서 $상호{\displaystyle }$ 접선 초구의 최대 수는 ${\displaystyle \mathrm{n}}$+ 2 ${\displaystyle$ n$+2$입니다.예를 들어, 3차원 공간에서는 5개의 구체가 상호 접선할 수 있습니다.초구의 곡률은 다음을 만족합니다.

$케이스$ ${\displaystyle {ki}_{}}$ = ${\displaystyle 0}$ ${\displaystyle k_{i$}=$0}$이 평평한 초평면에 해당하여 2차원 버전의 정리를 일반화합니다.복소수의 3차원 유사체는 없지만 중심 위치 간의 관계는 행렬 방정식으로 다시 표현할 수 있으며$,$ 이 방정식은 n개의 {\$displaystyle$ n$}$으로도 ^[17]일반화됩니다.

3차원에서, 3개의 상호 접선 구가 고정되어 있고, 3개의 고정 구에 접선하는 4번째 $구{\displaystyle {}_{}}$ ${\displaystyle {S1\mathrm{}}_{}}${\$displaystyle$ S_${1}}$이 주어졌다고 가정합니다.데카르트 정리의 3차원 버전은 S1 {\displaystyle S_{1}}에 접하는 구 S2 {\displaystyle S_{2}}와 고정 구를 구하는데 적용한 후, 다시 S2 {\displaystyle S_{2}에 접하는 새로운 구 S3 {\displaystyle S_{3}와 고정 구를 구하는데 적용할 수 있다.그 결과,^[15][47] 1936년에 소디가 발견하고 다른 시의 형태로 출판한 후, 그 수열에서 각각 이웃한 구와 세 개의 고정된 구에 접하는 여섯 개의 순환열과 소디의 육각형이라고 불리는 구성이 되었습니다.

구면 또는 쌍곡 기하학에서 상호 접선 초구의 고차원 구성은 위와 같이 정의된 곡률을 만족합니다.

$구면$ 기하학에서 C = ${\displaystyle 2}${\$displaystyle$ C=2$}, 쌍곡$ 기하학에서 C = - 2$${\$displaystyle$ C=-$2}.$

참고 항목

• 원 안에 원 패킹(circle packing
• 오일러의 4제곱 항등식
• 말파티 서클

참고문헌