입체 사영
Stereographic projection
| 시리즈의 일부(on) |
| 그래픽 프로젝션 |
|---|
 |
수학에서 입체 사영은 구의 특정 지점(극 또는 사영의 중심)을 지나 그 지점을 지나는 지름에 수직인 평면(사영면)으로 구를 원근법으로 투영하는 것입니다.투영 중심을 제외한 구 전체에서 평면 전체에 이르기까지 매끄럽고 투영적인 기능입니다.구면의 원을 평면의 원 또는 선에 매핑하고 등각형이며, 곡선이 만나는 각도를 보존하므로 국소적으로 대략적인 모양을 보존합니다.등각(거리 보존)도 아니고 등각(면적 보존)도 아닙니다.[1]
입체 사영은 평면으로 구를 표현하는 방법을 제공합니다.평면에서 구면으로의 역입체 투영에 의해 유도된 메트릭은 평면 내의 점들 사이의 지오데식 거리를 표현하는 구면 점들 사이의 구면 거리와 동일하게 정의합니다.입체 평면의 2차원 좌표계는 구형 극좌표나 3차원 데카르트 좌표 대신 구형 분석 기하학의 대안적인 설정입니다.이것은 쌍곡면의 푸앵카레 원반 모델의 구형 유사체입니다.
직관적으로, 입체 사영은 피할 수 없는 타협이 있는 구를 평면으로 묘사하는 방법입니다.구와 평면은 수학과 그 응용의 많은 분야에서 나타나기 때문에 입체 사영 또한 마찬가지입니다. 그것은 복잡한 분석, 지도 제작, 지질학, 사진학을 포함한 다양한 분야에서 사용됩니다.때때로 입체 연산은 입체망이라고 불리는 특수한 종류의 그래프 종이를 사용하여 그래픽으로 수행되며, 입체망 또는 울프망으로 단축됩니다.
역사

입체 사영은 히파르코스, 프톨레마이오스 그리고 아마도 더 이른 이집트인들에게 알려져 있었습니다.그것은 원래 평면구 투영으로 알려져 있었습니다.[2]프톨레마이오스에 의한 플라니스파륨은 현존하는 가장 오래된 문서입니다.그것의 가장 중요한 용도 중 하나는 천체도의 표현이었습니다.[2]평면구(Planisphere)라는 용어는 여전히 이러한 차트를 지칭하는 데 사용됩니다.
16세기와 17세기에, 입체 사영의 적도적인 측면은 동서양의 지도에 일반적으로 사용되었습니다.이미 1507년에 Gualterius Lud에[3] 의해 만들어진 지도가 입체 사영으로 되어 있었고, 후에 Jean Roze (1542), Rumold Mercator (1595), 그리고 다른 많은 사람들의 지도들도 마찬가지였다고 믿어집니다.[4]항성 도표에서, 이 적도적인 면조차도 프톨레마이오스와 같은 고대 천문학자들에 의해 이미 활용되었습니다.[5]
프랑수아 다길론(François d'Aguilon)은 1613년 그의 작품인 Opticorum librix philosis junstaac mathematicalisutiles (광학 여섯 권, 철학자와 수학자 모두에게 유용함)에서 입체 사영에 현재의 이름을 부여했습니다.[6]
16세기 후반, 토마스 해리엇은 입체 사영이 등각적이라는 것을 증명했습니다. 그러나, 이 증명은 결코 출판되지 않았고 3세기 이상 동안 그의 논문들 가운데 상자 안에 있었습니다.[7]1695년 Edmond Halley는 별 차트에 대한 그의 관심에 자극을 받아 증명을 처음으로 발표했습니다.[8]그는 그의 친구 아이작 뉴턴에 의해 발명된 최근에 만들어진 미적분학 도구를 사용했습니다.
정의.
제1제식

3차원 공간 R의 단위 구 S는 x + y + z = 1이 되는 점 (x, y, z)의 집합입니다. N = (0, 0, 1)을 "북극"이라 하고, M을 구의 나머지라고 합니다.평면 z = 0은 구의 중심을 지나며, "equator"은 이 평면과 구의 교차점입니다.
임의의 점 P에 대하여 N과 P를 통한 고유한 선이 존재하며, 이 선은 평면에 대한 P의 입체 사영으로 알려진 정확히 한 점 P'에서 평면 z = 0과 교차합니다.
구면의 직각좌표 (x, y, z)와 평면의 (X, Y)에서, 사영과 그 역은 공식으로 주어집니다.
구면 상의 구면 좌표(φ, θ)(제니스 각도 φ, 0≤φ ≤π, 방위각 θ, 0≤θ ≤2π) 및 평면 상의 극좌표(R, θ)에서 투영과 그 역은
여기서 φ는 R = 0일 때 값 π을 갖는 것으로 이해됩니다. 또한 삼각 항등식을 이용하여 이 수식들을 다시 쓰는 방법은 여러 가지가 있습니다.구면의 원통좌표(r, θ, z)와 평면의 극좌표(R, θ)에서 투영과 그 역은
기타 규약
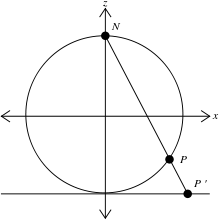
일부 저자는 북극(0, 0, 1)에서 남극(0, 0, -1)의 단위 구와 접하는 평면 z = -1로의 입체 사영을 정의합니다.이것은 위에서 설명한 적도면에 대한 투영, 그리고 그것으로부터 극면까지의 동형성의 구성으로 설명될 수 있습니다.동형성은 이미지를 2배(구면의 반지름에 대한 지름의 비율)만큼 축척하므로, 이 투영에 의해 생성된 값 X와 Y는 앞 절에서 설명한 적도 투영에 의해 생성된 값의 정확히 두 배입니다.예를 들어, 이 투영은 적도를 원점에 중심을 둔 반지름 2의 원으로 보냅니다.적도 투영은 적도를 따라 무한소 면적 왜곡을 일으키지 않지만, 극 접선 투영은 대신 남극에서 무한소 면적 왜곡을 일으키지 않습니다.
다른 저자들은 반지름 1/2의 구와 평면 z = -1/2를 사용합니다.이 경우 공식은

일반적으로 구면의 임의의 점 Q로부터 임의의 평면 E로의 입체 사영을 정의할 수 있습니다.
- E는 Q를 통해 직경에 수직이고,
- E는 Q를 포함하지 않습니다.
E가 이러한 조건을 만족하는 한, Q를 제외한 임의의 점 P에 대해 P와 Q 사이의 선은 정확히 한 점 P'에서 E를 만납니다. 이것은 P에서 E로의 입체 사영으로 정의됩니다.[11]
일반화
보다 일반적으로 입체 사영은 (n + 1)차원 유클리드 공간 E의n+1 단위 n-sphere S에n 적용될 수 있습니다.만약 Q가 S의 점이고 E가 E의 초평면이라면, 점 P ∈ S - {Q}의 입체 사영은 선 QP와 E의 교차점 P'입니다.S의 직각좌표 (x, i는 0에서 n까지)와 E의 (X, i는 1에서 n까지)에서 Q = (1, 0, 0, ..., 0) ∈ S로부터의 사영은 다음과 같이 주어집니다.
좀 더 일반적으로, S가 투영 공간n+1 P에 있는 (비단수) 쿼드릭 초표면이라고 가정합니다.다시 말해, S는 동차 좌표i x에서 비단수 이차 형식 f(x0, ..., xn+1)의 0의 궤적입니다. S의 임의의 점 Q와 Q를 포함하지n+1 않는 P의 초평면 E를 고정시키십시오.그렇다면 S - {Q}에서 점 P의 입체 사영은 QP와 E의 독특한 교점입니다.이전과 마찬가지로, 입체 투영은 "작은" 집합 밖에서 등각적이고 가역적입니다.입체 사영법은 쿼드릭 초표면을 합리적인 초표면으로 보여줍니다.[12]이 구조는 대수기하학과 등각기하학에서 역할을 합니다.
특성.
앞 절에서 정의한 첫 번째 입체 사영은 단위구의 "남극" (0, 0, -1)을 (0, 0)으로 보내고, 적도는 단위 원으로, 남반구는 원 안의 영역으로, 북반구는 원 밖의 영역으로 보냅니다.
투영점 N = (0, 0, 1)에서는 투영이 정의되지 않습니다.이 점의 작은 이웃들은 (0, 0)에서 멀리 떨어진 비행기의 부분집합으로 보내집니다.P가 (0, 0, 1)에 가까울수록 이미지가 평면에서 (0, 0)으로부터 더 멀리 떨어져 있습니다.이러한 이유로 (0, 0, 1)을 평면에서 "무한"으로 매핑하고, 구를 무한대에 점을 추가하여 평면을 완성하는 것으로 말하는 것이 일반적입니다.이 개념은 투영 기하학과 복잡한 분석에서 유용성을 발견합니다.단지 위상학적 수준에서, 그것은 구가 평면의 1점 압축과 어떻게 동형인지를 보여줍니다.
데카르트 좌표에서 구면 위의 점 P(x, y, z)와 평면 위의 점 P'(X, Y)는 둘 다 유리점이거나 둘 중 하나도 아닙니다.


입체 사영은 등각이며, 곡선이 서로 교차하는 각도를 보존한다는 의미입니다(그림 참조).반면에, 입체 사영은 면적을 보존하지 않습니다; 일반적으로, 구의 한 영역의 면적은 평면에 대한 사영의 면적과 동일하지 않습니다.면적 요소는 다음과 같이 (X,Y) 좌표로 제공됩니다.
X + Y = 1인 단위 원을 따라 한계 내의 면적 팽창이 없으므로 척도 인자가 1이 됩니다.(0, 0) 근처의 영역은 4배의 인자로 팽창되고, 무한대 근처의 영역은 임의로 작은 인자로 팽창됩니다.
메트릭은 다음과 같이 (X,Y) 좌표로 제공됩니다.
베른하르트 리만의 기하학 기초에 관한 하빌리츠 문서에서 발견되는 독특한 공식으로, 1854년 괴팅겐에서 전달되었고, "위베르 다 가설의 우물가 기하학자"라는 제목이 붙여졌습니다.
구에서 평면으로의 어떤 지도도 등각적이고 면적을 보존할 수 없습니다.그렇다면 국소 등각법이 되고 가우스 곡률을 보존할 수 있습니다.구와 평면은 가우스 곡률이 다르기 때문에 불가능합니다.
투영 지점을 통과하지 않은 구면의 원은 평면의 원으로 투영됩니다.[13][14]투영점을 통과하는 구면 위의 원은 평면 위의 직선으로 투영됩니다.이 선들은 때때로 무한대의 점을 통과하는 원 또는 무한반지름의 원으로 간주됩니다. 속성은 §에 주어진 X의 표현식을 X,Z의 표현식을 사용하여 확인할 수 있습니다. 첫 번째 공식화: 구면 위의 원을 포함하는 평면의 + - = + cz - d = 의 치환을 위해 이 표현식을 사용합니다.inators는 원의 방정식, 즉 -)( + ) - d) ( + )와 함께 2차 방정식을 얻습니다.를 그 이차 부분으로 합니다. = c = 인 경우, 즉 평면이 투영점을 통과하는 경우 방정식은 선형이 됩니다.
평면의 모든 선은 입체 사영의 역순으로 구면 위의 원으로 변환될 때 투영점에서 만납니다.평면에서 교차하지 않는 평행선은 투영점에서 접선하는 원으로 변환됩니다.교차하는 선들은 구면의 두 점에서 가로로 교차하는 원들로 변환되는데, 그 중 하나가 투영점입니다. (유사한 발언은 실제 투영면에 대한 것이지만, 그곳의 교차 관계는 다릅니다.)

형상의 평면에서 구면 지도에서 곡선까지의 로코드롬
여기서 매개변수 a는 록소드롬의 "긴박함"을 측정합니다.따라서 loxodromes는 로그 나선에 해당합니다.이 나선형들은 평면의 방사상 선들과 동일한 각도로 교차합니다. 마치 복소형들이 구면의 자오선들과 동일한 각도로 교차하는 것처럼 말입니다.

입체 사영은 평면 반전과 간단한 방법으로 관련이 있습니다.P와 Q를 구면 위의 두 점과 평면 위에 P'와 Q'를 투영한다고 가정합니다.그렇다면 P'와 Q'는 적도면에서 P와 Q가 서로의 반사일 경우에만 적도원의 이미지에서 서로의 역상입니다.
즉, 다음과 같은 경우:
- P는 구의 한 점이지만, '북극' N이 아니고, 대극인 '남극' S가 아닙니다.
- P'는 투영점 N을 갖는 입체 사영에서의 P의 이미지이고,
- P ″는 투영점 S를 갖는 입체 사영에서의 P의 이미지,
그러면 P'와 P ″는 단위 원에서 서로의 역상입니다.
울프넷

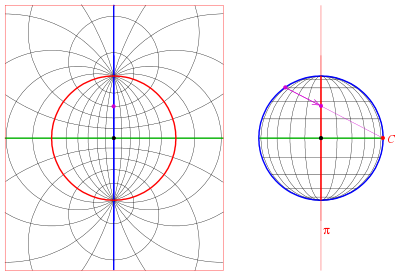
입체 투영도는 위에 제시된 명시적 공식을 사용하여 컴퓨터에서 수행할 수 있습니다.그러나 손으로 그래프를 그리는 경우에는 이러한 공식이 실행 불가능합니다.대신 작업을 위해 특별히 설계된 그래프 용지를 사용하는 것이 일반적입니다.이 특별한 그래프 종이는 러시아 광물학자 George (유리 빅토로비치) Wulff의 이름을 따 입체망 또는 Wulff 그물이라고 불립니다.[15]
여기에 표시된 울프망은 적도의 한 점(예를 들어 행성의 동쪽 또는 서쪽 반구)에 중심을 둔 반구의 평행선 및 자오선 격자의 입체 투영입니다.
그림에서 입체 투영의 영역 왜곡 특성은 그물 중앙 근처의 그리드 섹터와 맨 오른쪽 또는 왼쪽의 그리드 섹터를 비교하면 알 수 있습니다.두 부문은 구면에서 동등한 면적을 가지고 있습니다.디스크에서 후자는 전자의 4배에 가까운 면적을 가지고 있습니다.그리드를 더 미세하게 만들면 이 비율은 정확히 4에 가깝습니다.
울프 네트에는 평행선과 자오선의 상이 직각으로 교차합니다.이 직교성 특성은 입체 투영의 각도 보존 특성의 결과입니다.(단, 각도 보존 특성은 이 특성보다 강합니다.평행선과 자오선의 직교성을 보존하는 모든 투영이 각도 보존적인 것은 아닙니다.
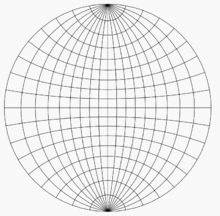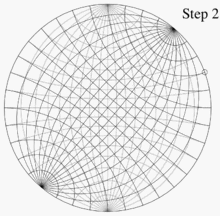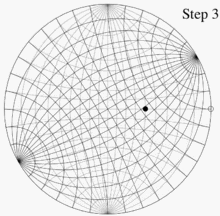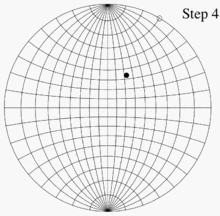
예를 들어, Wulff net을 사용하는 예를 들어, 얇은 종이 위에 두 개의 Wulff net을 올려놓고 서로의 중심에 정렬하고 접착하는 것을 상상해 보세요.P를 구면 좌표가 (140°, 60°)이고 데카르트 좌표가 (0.321, 0.557, -0.766)인 하위 단위 반구 상의 점이라 합니다.이 점은 양의 x축으로부터 시계 반대 방향으로 60°(양의 y축으로부터 시계 방향으로 30°), 수평면 z = 0보다 아래쪽으로 50° 방향을 향하는 선 위에 놓여 있습니다. 이 각도를 알면 P를 표시하는 데 4단계가 있습니다.
- 여기 그림에서 10° 간격으로 배치된 격자선을 사용하여 그물 가장자리의 점을 (1, 0) 지점에서 시계 반대 방향으로 60°(또는 (0, 1) 지점에서 시계 반대 방향으로 30°)로 표시합니다.
- 이 지점이 아래쪽 그물의 (1, 0)과 정렬될 때까지 위쪽 그물을 돌립니다.
- 아래쪽 그물의 격자선을 사용하여 그 지점에서 중심을 향해 50°인 지점을 표시합니다.
- 상단 그물을 이전 방향과 반대 방향으로 돌려 하단 그물과 다시 정렬합니다.3단계에서 표시된 점은 우리가 원하는 투영입니다.
각도가 60° 및 50°와 같은 둥근 숫자가 아닌 다른 점을 표시하려면 가장 가까운 격자선 사이에 시각적으로 보간해야 합니다.간격이 10°이상으로 촘촘한 그물이 있으면 도움이 됩니다.2° 간격은 일반적입니다.
입체도를 기준으로 구 위의 두 점 사이의 중심각을 찾으려면 그림을 울프 그물 위에 겹쳐 놓고 두 점이 자오선 위 또는 자오선 근처에 놓일 때까지 중심을 중심으로 회전합니다.그런 다음 자오선을 따라 격자선을 세어 그들 사이의 각도를 측정합니다.
-
두 점 P와1 P는2 울프 네트의 원점에 부착된 투명 시트에 그려집니다.
-
투명 시트는 회전하고 중앙 각도는 공통 자오선을 따라 두 점 P와1 P로2 읽힙니다.
수학 내의 응용 프로그램
복합분석
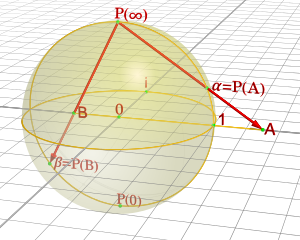
입체 투영에서는 구(투영점) 상의 한 점이 누락되지만, 서로 다른 투영점에서 두 개의 투영을 사용하여 전체 구를 매핑할 수 있습니다.즉, 구면은 평면으로부터 두 개의 입체 매개변수화(투영의 역)에 의해 커버될 수 있습니다.매개변수화는 구면에 동일한 방향을 유도하도록 선택할 수 있습니다.함께, 그들은 구를 배향된 표면(또는 2차원 다양체)으로 설명합니다.
이 구조물은 복합해석에 있어 특별한 의미를 갖습니다.실수 평면의 점 (X,Y)은 복소수 ζ = X + iY로 식별할 수 있습니다.북극에서 적도면으로의 입체 사영은 다음과 같습니다.
마찬가지로, ξ = X - iY를 또 다른 복잡한 좌표로 둔다면, 함수
남극에서 적도면으로의 입체 사영을 정의합니다.ζ coordin율과 ξ ξ율 사이의 전이 맵은 ζ = 1/ζ 및 ξ = 1/ξ이며, ζ이 무한대로 갈수록 0에 가까워지고, 그 반대도 마찬가지입니다.이것은 복소수에 대한 우아하고 유용한 무한 개념과 실제로 리만 구에 매핑되는 전체 형이상 함수 이론을 용이하게 합니다.단위구의 표준 메트릭은 리만 구의 푸비니-연구 메트릭과 일치합니다.
선과 평면의 시각화

3차원 공간에서 원점을 지나는 모든 선들의 집합은 실제 투영 평면이라고 불리는 공간을 형성합니다.이 평면은 3차원 공간에 내장될 수 없기 때문에 시각화하기가 어렵습니다.
그러나 다음과 같이 디스크로 시각화할 수 있습니다.원점을 통과하는 모든 선은 남반구 z ≤ 0과 한 점에서 교차하며, 이 점은 XY 평면에 있는 디스크의 한 점에 입체적으로 투영될 수 있습니다.원점을 통과하는 수평선은 적도를 따라 두 개의 반모달 지점에서 남반구와 교차하며 원반의 경계로 돌출합니다.두 투영점 중 하나는 디스크의 일부로 간주될 수 있습니다. 적도의 반모달 점은 3개 공간의 단일 선과 투영 디스크 경계의 단일 점을 나타내는 것으로 이해됩니다(계수 위상 참조).따라서 원점을 통과하는 선의 집합은 투영된 디스크의 점의 집합으로 나타낼 수 있습니다.그러나 경계점은 일반적인 2차원 디스크의 경계점과 다르게 작용하는데, 이들 중 하나는 디스크의 반대쪽 내부점에 동시에 가깝기 때문입니다(원점을 통과하는 거의 수평에 가까운 두 개의 선이 디스크의 반대쪽 점에 투영될 수 있는 것처럼).
또한 원점을 통과하는 모든 평면은 평면의 궤적이라 불리는 거대한 원 안에서 단위 구와 교차합니다.이 원은 입체 사영하에서 원에 매핑됩니다.따라서 투영을 통해 평면을 디스크의 원호로 시각화할 수 있습니다.컴퓨터가 보급되기 전에는, 원이 큰 입체 사영은 종종 빔 컴퍼스를 사용해야 하는 큰 반지름 호를 그리는 것을 포함했습니다.이제 컴퓨터가 이 작업을 훨씬 쉽게 해줍니다.
각각의 평면과 더 연관된 것은 원점을 통과하고 평면에 수직인 평면의 극이라고 불리는 독특한 선입니다.이 선은 원점을 통과하는 모든 선과 마찬가지로 디스크의 점으로 표시할 수 있습니다.따라서 입체 투영을 통해 평면을 디스크의 점으로 시각화할 수도 있습니다.많은 평면을 포함하는 그림의 경우 극을 그리는 것이 추적을 그리는 것보다 덜 산란된 그림을 만듭니다.
이 구조는 아래에 설명된 바와 같이 결정학 및 지질학에서 방향성 데이터를 시각화하는 데 사용됩니다.
기타 시각화
입체 사영법은 폴리토페의 시각화에도 적용됩니다.슐레겔 다이어그램에서, R의n+1 n차원 폴리토프는 n차원 구에 투영되고, 그 다음 R에n 입체적으로 투영됩니다.R에서n+1 R로n 줄이면 폴리토프를 시각화하고 이해하기 쉽게 만들 수 있습니다.
산술기하학

기초 산술 기하학에서 단위 원으로부터의 입체 사영은 모든 원시 피타고라스의 세 배를 설명하는 수단을 제공합니다.특히 북극(0,1)에서 x축으로의 입체 투영은 단위 원 위의 유리수 점(x, y)과 x축의 유리수 점 사이에 일대일 대응 관계를 제공합니다(y ≠ 1 포함).만약 (m/n, 0)이 x축의 유리점이라면, 그 역입체 투영은 점입니다.
유클리드의 피타고라스 3배 공식이 주어집니다.
접선반각치환
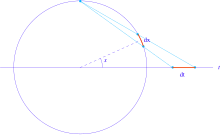
삼각 함수 쌍(sin x, cos x)은 단위 원을 매개 변수화하는 것으로 간주할 수 있습니다.입체 투영은 단위 원의 다른 매개 변수화를 제공합니다.
이 매개변수화 하에서 단위 원의 길이 요소 dx는
이러한 치환은 삼각함수를 포함하는 적분을 단순화할 수 있습니다.
기타 분야에 적용
지도 제작
지도 제작의 근본적인 문제는 구체에서 평면까지의 어떤 지도도 각도와 영역을 정확하게 나타낼 수 없다는 것입니다.일반적으로 지역 보존형 지도 투영은 통계적 응용에 선호되고, 각도 보존형(conformal) 지도 투영은 탐색에 선호됩니다.
입체 사영은 두 번째 범주에 속합니다.프로젝션이 지구의 북극 또는 남극에 중심을 맞출 경우 다음과 같은 추가적인 바람직한 특성이 있습니다.그것은 기원에서 뿜어져 나오는 광선에 경락을 보내고, 기원에서 중심이 되는 원에 평행을 이룹니다.
-
30°S 이북 세계의 입체 사영.15° 격자.
-
티샷의 변형 지표를 이용한 입체 사영.
행성학

입체는 구면의 모든 원을 평면의 원에 매핑하는 유일한 투영입니다.이 특성은 분화구가 전형적인 특징인 행성 지도 제작에 유용합니다.투영점을 통과하는 원들의 집합은 무한한 반지름을 가지므로 선으로 퇴화됩니다.
결정학

결정학에서, 3차원 공간에서 결정 축과 면의 방향은 X선 및 전자 회절 패턴의 해석과 같은 중심 기하학적 관심사입니다.위의 선 및 평면 시각화 섹션에서와 같이 이러한 방향을 시각화할 수 있습니다.즉, 결정축과 극에서 결정면까지 북반구와 교차한 다음 입체 사영을 사용하여 플롯합니다.극의 플롯은 극 도형이라고 불립니다.
전자 회절에서 키쿠치 선쌍은 격자 평면 흔적과 에발트 구 사이의 교차점을 장식하는 띠로 나타나 결정의 입체 사영에 대한 실험적 접근을 제공합니다.상호 공간의 모델 키쿠치(Kikuchi) 맵과 [16]직접 공간의 벤드 윤곽과 함께 사용하기 위한 프린지 가시성 맵은 투과 전자 현미경의 결정으로 방향 공간을 탐색하기 위한 로드 맵으로 작용합니다.[17]
지질학

구조 지질학의 연구자들은 여러 가지 이유로 평면과 선의 방향에 관심을 갖습니다.암석의 엽리는 평면 형상으로, 종종 선형 형상이라 불리는 선형 형상을 포함합니다.마찬가지로 결함 평면은 슬리큰 측면과 같은 선형 특징을 포함할 수 있는 평면 특징입니다.
위의 선 및 평면 시각화 섹션의 방법을 사용하여 다양한 스케일의 선 및 평면 방향을 플롯할 수 있습니다.결정학에서와 마찬가지로 평면은 일반적으로 극으로 표시됩니다.결정학과 달리, 남반구는 북반구 대신에 사용됩니다. (문제의 지질학적 특징이 지구 표면 아래에 있기 때문입니다.)이러한 맥락에서 입체 사영은 종종 등각 하반구 사영으로 언급됩니다.Lambert 방위각 등면적 투영법에 의해 정의된 등면적 저반구 투영법도 사용되며, 특히 플롯이 밀도 등고선화와 같은 후속 통계 분석의 대상이 될 때 사용됩니다.[18]
포토그래피


일부 어안 렌즈는 광각 시야를 포착하기 위해 입체 투영을 사용합니다.[19]동일한 면적의 프로젝션을 사용하는 기존의 어안 렌즈에 비해 가장자리에 가까운 부분은 모양을 유지하고 직선은 덜 휘어져 있습니다.그러나 입체 어안 렌즈는 일반적으로 제조 비용이 더 비쌉니다.[20]Panotools와 같은 이미지 재매핑 소프트웨어는 동일한 면적의 어안에서 입체 투영으로 사진을 자동 재매핑할 수 있습니다.
입체 사영은 1779년 호레이스 베네딕트 드 소슈르를 시작으로 구면 파노라마 지도를 그리는 데 사용되었습니다.이로 인해 작은 행성(투영 중심이 나디르일 때)과 튜브(투영 중심이 제니스일 때)로 알려진 효과가 발생합니다.[21]
입체 투영을 사용하여 다른 방위 투영에 비해 파노라마를 매핑하는 인기는 투영의 적합성으로 인한 형상 보존에 기인합니다.[21]
참고 항목
- 지도 투영도 목록
- 아스트롤라베
- 천문시계
- Poincaré 디스크 모델, 쌍곡면의 유사한 매핑
- 지도 제작에서의 입체 사영
참고문헌
- ^ 평면의 유클리드 미터법 아래에서.
- ^ a b 스나이더 (1993).
- ^ (Snyder 1993)에 따르면, 비록 그가 그것을 개인적으로 보지 않았다고 인정하지만,
- ^ 스나이더 (1989)
- ^ Brown, Lloyd Arnold : 지도 이야기, p.59
- ^ 에케르트를 언급하는 엘킨스(Ekins, 1988)에 따르면, 1921년 베를린, 121-123쪽
- ^ Lohne, John (1979). "Essays on Thomas Harriot". Archive for History of Exact Sciences. 20 (3/4): 189–312. doi:10.1007/BF00327737. S2CID 118095486.
- ^ 티모시 페이먼.2002년 "지구의 초상: 지도를 보는 수학자"미국 수학 학회.
- ^ Cf. Apostol (1974) p. 17.
- ^ 겔판드, 민로스 & 샤피로 1963
- ^ Cf. Pedoe (1988).
- ^ Cf. Shafarevich (1995).
- ^ Ahlfors, Lars (1966). Complex Analysis. McGraw-Hill, Inc. p. 19.
- ^ Conway, John; Doyle, Peter; Gilman, Jane; Thurston, Bill (1994-04-12), "Stereographic Projection", Geometry and the Imagination in Minneapolis, Minnesota University, arXiv:1804.03055, archived from the original on 2021-04-19, retrieved 2022-04-26
- ^ 울프, 조지, 운터수충겐 임 게비에테 데 옵티셴 아이겐샤프텐 이소모르퍼 크리스탈레: 자이트.Krist.,36,1-28 (1902)
- ^ M. von Heimendahl, W. Bell 그리고 G.Thomas (1964) 전자현미경에서의 키쿠치 선 분석의 응용, J. Appl. 신체검사 35:12, 3614–3616
- ^ P. 프라운도르프, 웬타오친, P.Moeck and Eric Mandell (2005) 나노결정 격자무늬의 이해, J. Appl. 신체검사 98:114308
- ^ Lisle, R.J.; Leyshon, P.R. (2004). Stereographic Projection Techniques for Geologists and Civil Engineers (2 ed.). Cambridge University Press. ISBN 9780521535823.
- ^ 삼양 8mm f/3.5 어안 CS 웨이백 머신에서 보관 2011-06-29
- ^ "Samyang 8 mm f/3.5 Aspherical IF MC Fish-eye". lenstip.com. Retrieved 2011-07-07.
- ^ a b 독일 외.(2007).
원천
- Apostol, Tom (1974). Mathematical Analysis (2 ed.). Addison-Wesley. ISBN 0-201-00288-4.
- Brown, James & Churchill, Ruel (1989). Complex variables and applications. New York: McGraw-Hill. ISBN 0-07-010905-2.
- Casselman, Bill (2014), Feature column February 2014:Stereographic Projection, AMS, retrieved 2014-12-12
- German, Daniel; Burchill, L.; Duret-Lutz, A.; Pérez-Duarte, S.; Pérez-Duarte, E.; Sommers, J. (June 2007). "Flattening the Viewable Sphere". Proceedings of Computational Aesthetics 2007. Banff: Eurographics. pp. 23–28.
- Gelfand, I.M.; Minlos, R.A.; Shapiro, Z.Ya. (1963), Representations of the Rotation and Lorentz Groups and their Applications, New York: Pergamon Press
- Do Carmo; Manfredo P. (1976). Differential geometry of curves and surfaces. Englewood Cliffs, New Jersey: Prentice Hall. ISBN 0-13-212589-7.
- Elkins, James (1988). "Did Leonardo Develop a Theory of Curvilinear Perspective?: Together with Some Remarks on the 'Angle' and 'Distance' Axioms". Journal of the Warburg and Courtauld Institutes. The Warburg Institute. 51: 190–196. doi:10.2307/751275. JSTOR 751275. S2CID 193430645.
- Oprea, John (2003). Differential geometry and applications. Englewood Cliffs, New Jersey: Prentice Hall. ISBN 0-13-065246-6.
- Pedoe, Dan (1988). Geometry. Dover. ISBN 0-486-65812-0.
- Shafarevich, Igor (1995). Basic Algebraic Geometry I. Springer. ISBN 0-387-54812-2.
- Snyder, John P. (1987). Map Projections − A Working Manual, Professional Paper 1395. US Geological Survey.
- Snyder, John P. (1989). An Album of Map Projections, Professional Paper 1453. US Geological Survey.
- Snyder, John P. (1993). Flattening the Earth. University of Chicago. ISBN 0-226-76746-9.
- Spivak, Michael (1999). A comprehensive introduction to differential geometry, Volume IV. Houston, Texas: Publish or Perish. ISBN 0-914098-73-X.
외부 링크
- Weisstein, Eric W. "Stereographic projection". MathWorld.
- Wayback Machine on Planet Math에서 2013-03-10 스테레오그래픽 프로젝션 아카이브
- 절단된 매듭으로부터의 입체 사영과 반전
- DoITPoMS 교수 학습 패키지 - "The Stereographic Projection"
비디오
소프트웨어
- Rick Allmender의 구조 지질학 소프트웨어 도구 Stereonet.
- PTCLab, 상변환 결정학 실험실
- 스페리카, 입체 투영 디스플레이 옵션을 포함한 구면의 직선 및 나침반 구축을 위한 소프트웨어
- 3차원 자바 애플릿
- Estereografica Web, Ernesto Cristallini의 구조 지질학 및 단층 운동학에서의 입체 사영을 위한 웹 애플리케이션.










 그 이차 부분으로 합니다.
그 이차 부분으로 합니다.












