이산 라플라스 연산자

이 글은 검증을 위해 인용구가 추가로 필요하다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선할 수 있도록 도와주십시오. 공급되지 않은 재료는 도전하여 제거할 수 있다. 출처 찾기: "Discrete Laplace Operator" – 뉴스 · 신문 · 책 · 학자 · JSTOR (2007년 12월) (이 템플릿 메시지를 제거하는 방법과 시기 학습)

수학에서 이산형 라플라스 연산자는 연속형 라플라스 연산자의 아날로그로, 그래프나 이산형 그리드에 의미를 가지도록 정의된다.유한 치수 그래프의 경우(가장자리와 꼭지점의 수가 한정되어 있음) 이산 라플라스 연산자를 더 흔히 라플라스 행렬이라고 부른다.

이산 라플라스 연산자는 이산 동력학 시스템의 연구뿐만 아니라 Ising 모델과 루프 양자 중력과 같은 물리학 문제에서 발생한다.연속 라플라스 연산자를 위한 스탠드인(stand-in)으로서 수치해석에서도 사용된다.일반적인 응용 프로그램으로는 라플라스 필터로 ^[1]알려진 이미지 처리와 클러스터링용 머신러닝, 근린 그래프의 준감독 학습 등이 있다.

정의들

그래프 라플라시안

부호 및 척도 인자에 따라 다르며, 그래프에 대한 이산 라플라시아어의 정의는 다양하다(때로는 주변 정점에 대한 평균 한 개, 때론 단순히 합쳐서 한 개, 이것은 일반 그래프에 대해 아무런 차이가 없다).아래 주어진 그래프의 전통적인 정의는 자유경계가 있는 도메인에서 음의 연속성 라플라시안에 해당한다.

$G{\displaystyle }$=${\displaystyle }$( ${\displaystyle V}$, E${\displaystyle }$) ${\displaystyle G=(V,E)}$은 $정점{\displaystyle }$ V$${\$displaystyle V}$과 $가장자리{\displaystyle }$ E$${\$displaystyle E}$을(를) 가진 그래프$$$.$ let $\varphi {\displaystyle }$: ${\displaystyle V}$→ ${\displaystyle R}$ ${\displaystyle \colon V\to R}$은 정점 값을 갖는 정점 함수.그런 다음 $discrete{\displaystyle }$ ${\displaystyle \$$Delta }$에 작용하는$$ 이산 Laplacian $\Delta {\displaystyle \mathrm{}}$ ${\displaystyle \$$pi }$에 의해 정의된다.

${\delta \phi )(v)=\sum _{w:\,d(w,v)=1}왼쪽[\phi(v)-\phi(w)\오른쪽]}$

여기서 $d{\displaystyle }$( ${\displaystyle w}$, ${\displaystyle v}$) ${\displaystyle d(w,v)}$은 정점 w와 v 사이의 그래프 거리입니다.따라서 이 합계는 정점 v의 가장 가까운 이웃에 걸쳐 있다.에지와 정점의 수가 유한한 그래프의 경우, 이 정의는 라플라시안 행렬의 정의와 동일하다.That is, ${\displaystyle \phi }$ can be written as a column vector; and so ${\displaystyle \Delta \phi }$ is the product of the column vector and the Laplacian matrix, while ${\displaystyle (\Delta \phi )(v)}$ is just the v'th entry of the product vector.

그래프에 가중 에지, 즉 가중치 함수 $function{\displaystyle }$ :${\displaystyle }$E →${\displaystyle R}$ ${\displaystyle \gamma \colon$ E$\to$ R$}$이(가) 주어지면$$ 정의는 다음과 같이 일반화될 수 있다.

${\deltayle (\Delta _{\gamma }\phi )(v)=\sum _{w:\,d(w,v)=1}\gamma _{wv}\phi(v)-\phi(w)\right]}}$

여기서 $\gamma {\displaystyle {}_{}}$ ${\displaystyle w_{}}$ ${\displaystyle v_{}}$ ${\$은(는)$display$ E {\$displaystyle wv\in$ E$}$인 가장자리의 중량 값이다$.$

이산 Laplacian과 밀접하게 관련된 평균 연산자는 다음과 같다.

${\displaystyle (M\phi )(v)={\frac {1}{\deg v}\sum _{w:\,d(w,v)=1}\phi(w).}$

메쉬 라플라시안

메쉬 라플라스 연산자는 그래프에서 노드와 에지의 연결을 고려할 뿐만 아니라 표면의 기하학(예: 노드의 각도)을 고려한다.다지관 삼각망사의 경우, 정점 $i{\displaystyle }$ ${\displaystyle i}$에서 스칼라 함수 $u{\displaystyle }$ ${\displaystyle u}$의 라플라스-벨트라미 연산자는 다음과 같이 근사하게 추정할 수 있다$$.

${\displaystyle(\Delta u)_{i}\약 {\frac {1}{2A_{i}}}\sum _{j}(\cot \alpha _{ij}+\cot \beta _{ij})(u_{i}-u_{j}),}$

여기서 합계가 $i{\displaystyle }$ ${\displaystyle$ $i$$\},$ $\alpha {\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\displaystyle j_{}}$ ${\$ 및$$ $\beta {\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\displaystyle j}$ ${\displaystyle$ $\beta _{ij}$의 모든$$ 인접 $정점{\displaystyle }$ j ${\$$displaystytyle$ $ij$ $A_{i}$의 정점 영역이다$.$$playstyle i$ 즉, $i{\displaystyle }${\$displaystyle i$}에 발생한 삼각형 합계의 3분의 1이 된다$.$위의 등사 공식은 조각처럼 선형의 유한요소, 유한체적(유아에 대한 참조), 이산형 외부 미적분([1] 참조) 등 다양한 방법을 사용하여 도출할 수 있다.

To facilitate computation, the Laplacian is encoded in a matrix ${\displaystyle L\in \mathbb {R} ^{ V \times V }}$ such that ${\displaystyle Lu=(\Delta u)_{i}}$. Let ${\displaystyle C}$ be the (sparse) cotangent matrix with entries

${\displaystyle C_{ij}={\begin{cases}-{\frac {1}{2}}(\cot \alpha _{ij}+\cot \beta _{ij})&ij{\text{ is an edge}},\\-\sum \limits _{k\in N(i)}$$C_{ik}&i=j,\\0&{\\text{datawise,}\end{case}}$ 여기서 $){\displaystyle$ N$(i)}$은(는$)$ $i{\displaystyle }$ {\$displaystyle i}$의 주변을 가리킨다$$$.$

$그리고{\displaystyle }$ $M{\displaystyle }$ ${\displaystyle M}$을(를) 대각선 질량 행렬 $M{\displaystyle }$ ${\displaystyle i}$ -th번째 항목이$$ 대각선을 따라 정점 영역 ${\displaystyle A_{}}$ i ${\$인 대각선 질량 행렬 M {\$displaystystyle M}$이 되도록 한다$.$그${\displaystyle }다음{\displaystyle }$ ${\displaystyle {}^{}}$= ${\displaystyle {\mathrm{M}}^{}}$ - 1 ${\displaystyle {}^{}}$ ${\displaystyle L=M^{-1}C}$는 라플라시안을 탈고하고자 하는 것이다.

메쉬 오퍼레이터에 대한 보다 일반적인 개요가 에 제시되어 있다.^[3]

유한차이

유한차분법 또는 유한요소법에 의해 얻은 라플라시안 근사치는 이산 라플라시안이라고도 할 수 있다.예를 들어, 2차원의 라플라시안(Laplacian)은 5점 스텐실 유한차분법을 사용하여 근사하게 추정할 수 있어 다음과 같은 결과를 얻을 수 있다.

${\displaystyle \Delta f(x,y)\약 {\f(x-h,y)+f(x,y-h)+f(x,y+h)+f(x,y+h)-4f(x,y)}{h^{2}}}$

여기서 격자 크기는 두 치수 모두 h이므로 격자 내 점(x, y)의 5점 스텐실

${\displaystyle \{(x-h,y),(x,y),(x+h,y),(x,y-h),(x,y+h)\}.}$

격자 크기 h = 1이면 그래프의 음의 이산 라플라시안이 정사각형 격자 격자인 것이다.격자 격자의 경계에는 함수 f(x, y)의 값에 대한 제약조건이 없기 때문에, 이는 경계에서 선원이 없는 경우, 즉 무플렉스 경계조건(일명, 절연 또는 동질 Neumann 경계조건)이다.경계에서 상태 변수의 제어는 격자 경계(일명 디리클레 경계 조건)에 주어진 f(x, y)로서 그래프 라플라시안에게는 거의 사용되지 않지만 다른 용도에서 공통적이다.

직사각형 큐빅 정규 그리드의 다차원 이산 라플라시안에는 매우 특별한 특성이 있다. 예를 들어, 그것들은 1차원 이산 라플라시안들의 크로네커 합이다. 이 경우 모든 고유값과 고유 벡터를 명시적으로 계산할 수 있다.

유한요소법

이 접근법에서 도메인은 더 작은 원소, 흔히 삼각형 또는 사방형 원소로 분해되지만, 직사각형이나 큐보이드와 같은 다른 원소들은 가능하다.그런 다음 솔루션 공간은 사전 정의된 수준의 소위 형태 기능을 사용하여 대략적으로 계산된다.그런 다음 라플라스 연산자를 포함하는 미분 방정식을 변이 공식으로 변환하고 방정식의 시스템을 구성한다(선형 또는 고유값 문제).결과 행렬은 대개 매우 희박하며 반복적인 방법으로 해결할 수 있다.

이미지 처리

이산 라플라스 연산자는 에지 검출 및 모션 추정 애플리케이션과 같은 이미지 처리에서 종종 사용된다.^[4]이산 라플라시안은 두 번째 파생상품인 라플라스 연산자#코디네이트 표현식의 합으로 정의되며 중심 픽셀의 가장 가까운 이웃에 대한 차이의 합으로 계산된다.파생 필터는 이미지의 노이즈에 민감한 경우가 많기 때문에, 파생 모델을 계산하기 전에 노이즈를 제거하기 위해 라플라스 연산자는 스무딩 필터(가우스 필터 등)를 선행하는 경우가 많다.스무딩 필터와 라플라스 필터는 종종 단일 필터로 결합된다.^[5]

운영자 분리를 통한 구현

1차원, 2차원 및 3차원 신호의 경우, 이산 라플라시안은 다음과 같은 커널을 가진 콘볼루션으로 주어질 수 있다.

1D 필터: → =[ 1- 2 ${\$

2D 필터: =[ - 4 ${\$\&#$1&#1&#1&0\end${bmatrix

${\displaystyle {\mathbf{D}}_{}^{}}$ ${\displaystyle {}_{}^{}}$ ${\displaystyle y_{}^{}}$ ${\displaystyle {\mathrm{}}_{}^{}}$ ${\$은 앞에서 본 (5점 스텐실) 유한차 공식에 해당한다$$.매우 다양한 분야에서 안정적이지만, 용액이 빠르게 변화하는 방정식의 경우 대각선을 포함하는 9점 스텐실처럼 ^[6]라플라시안 연산자의 안정적이고 등방성 형태가 필요하다.

2D filter: ${\displaystyle \mathbf {D} _{xy}^{2}={\begin{bmatrix}0.25&0.5&0.25\\0.5&-3&0.5\\0.25&0.5&0.25\end{bmatrix}}}$,

3D 필터: $D{\displaystyle {\mathbf{}}_{}^{}}$ x ${\displaystyle y_{}^{}}$ ${\displaystyle {\mathrm{}}_{}^{}}$ ${\displaystyle 2_{}^{}}$ ${\$ 7포인트 스텐실을 사용하여$$ 다음을 제공한다.

첫번째 비행기)[000010000]{\displaystyle{\begin{bmatrix}0&, 0&, 0\\0&, 1&, 0\\0&, 0&, 0\end{bmatrix}}};두번째 비행기)[0101−를 6대 1010]{\displaystyle{\begin{bmatrix}0&, 1&, 0\\1&, -6&, 1\\0&, 1&, 0\end{bmatrix}}};세번째 평면= -LSB- 000010000입니다. ${\$&0\0$&0\\0&0\end{bmatrix$

그리고 27 포인트 스텐실을 사용하는 방법:^[7]

첫번째 비행기)126[232363232]{\displaystyle{\frac{1}{26}}{\begin{bmatrix}2&, 3&, 2\\3&, 6&, 3\\2&, 3&, 2\end{bmatrix}}};두번째 비행기)126[3636− 886363]{\displaystyle{\frac{1}{26}}{\begin{bmatrix}3&, 6&, 3\\6&, -88&. 6.\\3&, 6&, 3\end{bmatrix}}};세번째 평면) [ ${\$

nD 필터:요소의$$ ${\displaystyle {경우{}_{}}_{}}$ 커널 $D{\displaystyle {\mathbf{}}_{}^{}}$ ${\displaystyle {{x\mathrm{}}_{}}_{}^{}}$ 1,${\displaystyle {{}_{}{}_{}}_{}}$${\displaystyle {{}_{}{}_{}}_{}^{}}$ ,${\displaystyle {{}_{}}_{}}$ ${\displaystyle {2_{}}_{}}$ , x n$${$x_{1},$${\displaystyle {{x\_\mathrm{}}_{}}_{}^{}}$${2},\dots,$${\displaystyle {{x\_}_{}}_{}^{}}$${n}},$$\displaystyle \mathbf {D} _{x_{1}, \dots,x_{n^{$n1},},{$n^},},},},},}$

${\displaystyle a_{x_{1},x_{2},\message,x_{n}=\loss}-2n&{{\loss{n},\1&{\text}{{if{s=n=n,\0&{\text},\end{array}}\rig}\rig}\rig}\right}}}}}}}}}}}}}}}}}}}}}오른쪽.}$

여기서 는 낟알에 있는 요소의 위치(-1, 0 또는 1)이다.i-th direction, 그리고 0이 되는 방향 수입니다.

라플라시안의 그래프 일반화에 기초하는 nD 버전은 모든 이웃이 동일한 거리에 있다고 가정하고, 따라서 위의 버전이 아닌 대각선이 포함된 다음과 같은 2D 필터로 이어진다는 점에 유의한다.

2D 필터: y =[ - 1 . ${\displaystyle \mathbf {D} _{xy}^{2}={\begin{bmatrix}1&1&1\1&$1\&#1$&1\end{bmatrix}.$$}$

이러한 커널은 이산형 차등 인용구를 사용하여 추론한다.

차동 연산자의 볼록한 조합으로서 2차원 라플라크 연산자의 다음과 같은 이산 근사치를 알 수 있다^[8][9].

${\displaystyle \nabla _{\gamma }^{2}=(1-\gamma )\nabla _{5}^{2}+\gamma \nabla _{\times }^{2}=(1-\gamma ){\begin{bmatrix}0&1&0\\1&-4&1\\0&1&0\end{bmatrix}}+\gamma {\begin{bmatrix}1/2&0&1/2\\0&-2&0\\1/2&0&1/2\end{bmatrix}}}$

γ의 경우, ∈ [0, 1]은 이산 스케일 공간 특성과 호환되며, 여기서 특히 γ = 1/3 값은 회전 대칭의 가장 좋은 근사치를 제공한다.^[8][9][10]3차원 신호와 관련하여, 라플라크 연산자는 2-모수 차이 연산자 계열에 의해 근사치 될 수 있음을 보여준다^[9].

${\displaystyle \nabla _{\gamma _{1},\gamma _{2}}^{2}=(1-\gamma _{1}-\gamma _{2})\,\nabla _{7}^{2}+\gamma _{1}\,\nabla _{+^{3}}^{2}+\gamma _{2}\,\nabla _{\times ^{3}}^{2}),}$

어디에

${\displaystyle (\nabla _{7}^{2}f)_{0,0,0}=f_{-1,0,0}+f_{+1,0,0}+f_{0,-1,0}+f_{0,+1,0}+f_{0,0,-1}+f_{0,0,+1}-6f_{0,0,0},}$

${\displaystyle (\nabla _{+^{3}}^{2}f)_{0,0,0}={\frac {1}{4}}(f_{-1,-1,0}+f_{-1,+1,0}+f_{+1,-1,0}+f_{+1,+1,0}+f_{-1,0,-1}+f_{-1,0,+1}+f_{+1,0,-1}+f_{+1,0,+1}+f_{0,-1,-1}+f_{0,-1,+1}+f_{0,+1,-1}+f_{0,+1,+1}-12f_{0,0,0}),}$

${\displaystyle (\nabla _{\times ^{3}}^{2}f)_{0,0,0}={\frac {1}{4}}(f_{-1,-1,-1}+f_{-1,-1,+1}+f_{-1,+1,-1}+f_{-1,+1,+1}+f_{+1,-1,-1}+f_{+1,-1,+1}+f_{+1,+1,-1}+f_{+1,+1,+1}-8f_{0,0,0}).}$

지속적인 재구성을 통한 구현

${\displaystyle 영상}$을 구성하는 이산 신호는 좌표 벡터 $r{\displaystyle \stackrel{}{}\in }$ ${\displaystyle {}^{}}$ ${\displaystyle n^{}}$ ${\$이(가) 있고 값 $도메인$이 ${\displaystyle \mathrm{실제}}$ f$display$ R {\$displaystyle f\in$ R$}$인 연속 함수 $("){\displaystystyle$f$\in$ R$}$의 이산 표현으로 볼 수 있다$.$ 여기서 파생 작업이 이루어진다.연속 기능인 $f{\displaystyle }$ ${\displaystyle f}$에 직접 적용할 수 있는 예$.$ 특히 탈소화 과정에 대한 합리적인 가정을 가진 이산형 영상, 예를 들어 밴드 제한 기능 또는 파장 확장 기능 등은 재구성의 기초가 되는 적절한 행동 보간 기능을 통해 재구성할 수 있다.이온 제형,^[11]

${\displaystyle f({\bar {r})=\sum _{k\in K}f_{k}\mu _{k}{\bar {r}}}}}$

여기서 ${\displaystyle f_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle R}$ ${\displaystyle f_{k}\in R}$은(는) $그리드{\displaystyle }$ K ${\displaystyle K}$에 $대한{\displaystyle }$ f ${\displaystyle f}$의 이산 표현이고 ${\displaystyle {\mu k}_{}}$ ${\$$displaystyle$ $\mu_{k}$은 그리드 $}$에 대한 보간 기능이다$.$ 이미지, 대역 제한 $기능$ 등 균일한 그리드에서 인터폴라.tion functions are shift invariant amounting to ${\displaystyle \mu _{k}({\bar {r}})=\mu ({\bar {r}}-{\bar {r}}_{k})}$ with ${\displaystyle \mu }$ being an appropriately dilated sinc function defined in ${\displaystyle n}$-dimensions i.e. ${\displaystyle \overline{r}=(x_1,x_{}}$${\$$x_{n}^{T$ 균일한 그리드에 있는$$ $\mu {\displaystyle }$ ${\displaystyle \mu }$의 기타 근사치는 $n{\displaystyle }$ ${\displaystyle n}$ -dimens로$$ 적절하게 확장된 가우스 함수를 사용한다.이에 따라 이산 라플라시안은 ${\displaystyle 연속\stackrel{}{}}$f${\displaystyle (\text{'}\text{'}}$ $){\displaystyle$ f$({\bar {r})}$의 이산형 라플라시안 버전이 된다.

${\displaystyle \nabla ^{2}f({\bar{r}_{k}}=\sum_{k'}{k'}(\nabla ^{2}\bar{r}-{r}-{r}}\bar{r}}) _{{r={r_{}}}}}}}}}}}}}}}$

즉, 균일한 (이미지) $그리드{\displaystyle }$ K ${\displaystyle K}$에 있는 보간 기능의 라플라크안과의 경합이다$.$ 보간 기능으로 가우스인을 사용하는 이점은 $f{\displaystyle }$ ${\displaystate$} 좌표 프레임의 회전 아티팩트가 없는 라플라크안을 포함한 선형 연산자를 산출한다는 것이다.$yle f}$은(는) $f{\displaystyle {}_{}}$ k ${\$ f_${k}$를 통해 $n{\displaystyle }$ ${\displaystyle n}$ -messages로$$ 표시되며$,$ 정의에$$ 따라 주파수를 인식한다.$선형{\displaystyle \stackrel{}{}}$ 연산자는 r$`{\$ 도메인에서$$ 제한된 범위를 가질 뿐만 아니라, 원칙적인 방식으로 가우스 영역의 분산을 통해 명시적으로 제어할 수 있는 주파수 영역(대안 가우스 스케일 공간)에서도 유효 범위를 가진다.$결과{\displaystyle }$ 필터링은 n ${\displaystyle n}$ -dimens의$$ 추가 계산 효율을 위해 분리 가능한 필터와 소멸(신호 처리)/피라미드(이미지 처리) 표현을 통해 구현할 수 있다.즉, 어떤 크기의 이산형 라플라시안 필터는 공간적 크기를 가진 가우스인의 라플라시안 표본이 분산에 의해 제어되는 특정 애플리케이션의 요구에 적합하게 샘플링됨으로써 편리하게 생성될 수 있다.비선형 연산자인 단원형도 신호가 충분히 과표본된 경우 유사한 재구성 및 근사치 접근방식을 사용하여 구현할 수 있다.따라서 그러한 비선형 연산자(예:방향 추정에 있어 전체 최소 제곱 최적성을 패턴 인식에 사용하는 Structure Tensor와 General Structure Tensor를 실현할 수 있다.

스펙트럼

무한 그리드 상의 이산 라플라시안 스펙트럼은 핵심 관심사로서, 자체 적응 연산자이기 때문에 실제 스펙트럼을 가진다.$Z$ ${\displaystyle Z}$의 Δ${\displaystyle }$= ${\displaystyle I}$- M ${\displaystyle \Delta =I-M}$ 규약의 경우 스펙트럼은${\displaystyle }$[ 0${\displaystyle ,}$ ${\displaystyle 2}$ ${\displaystyle ]}$ ${\displaystyle [0,$${\displaystyle 2}$$]}$ 내에 있다$($$$평균 연산자는${\displaystyle }$[${\displaystyle }$- ${\displaystyle 1}$,${\displaystyle ]}$ ${\displaystystyle [-1]}).$이는 푸리에 변환을 적용함으로써도 알 수 있다.무한 격자의 이산 라플라시안에는 순수하게 절대적으로 연속적인 스펙트럼이 존재하므로 고유값이나 고유특성은 없다는 점에 유의한다.

정리

그래프가 무한 사각 격자 격자라면, 라플라시아인의 이 정의는 무한정 미세한 격자 한계에서 연속적인 라플라시아어와 일치한다고 보여줄 수 있다.예를 들어, 1차원 그리드에서는

${\displaystyle {\frac {\partial ^{2}F}{\partial x^{2}}=\lim_{\epsilon \rightarrow 0}{{\frac {}{\epsilon )-F(x)]+[F(x-\epsilon )-F(x)}{\epsilon ^{2}}}}}.}$

라플라시안의 이 정의는 일반적으로 수치 분석과 이미지 처리에서 사용된다.이미지 처리에서, 그것은 디지털 필터의 한 종류, 더 구체적으로는 라플라스 필터라고 불리는 에지 필터로 간주된다.

이산열방정식

${\textstyle \phi}$이(가) 그래프 전체의 열 분포를 설명한다고$$ 가정합시다. 여기서 $\varphi {}_{}$ $i_{}$ ${\$는 $정점$ i ${\textstyle$ $i$$}$의 열입니다$.$ 뉴턴의 냉각 법칙에 따르면 노드 $i$ ${\$$textstyle i$$}$에서 노드 $j$ ${\$te$}$로 전달된 열은$$ $i_{}$ -${}_{}{}_{}$ $j_{}$에 비례합니다$.$$xtstyle \phi _{i}-\phi$ $\_$${j}$ 노드 i ${\textstyle i}$와 j ${\textstyle j}$이(가) 연결된 경우$$(연결되지 않은 경우 열이 전달되지 않음)그런 다음, 열 $용량$ k$${\$textstyle k}$의 경우$,$

${\displaystyle{\begin{정렬}{\frac{d\phi_{나는}}{dt}}&=-k\sum _ᆯA_ᆰ\left(\phi_{나는}-\phi_{j}\right)\\&, =-k\left(\phi_{나는}\sum_{j}A_{ij}-\sum_{j}A_{ij}\phi_{j}\right)\\&, =-k\left(\phi_{나는})\deg(v_{나는})-\sum _{j}A_{ij}\phi _{j}\right)\\&, =-k\sum _ᆴ\left(\delta_{ij})\deg(v_{나는})-A_{ij}\right)\phi _{j}\\&, =-k\sum _{j}\left(.L_{ij}\right)\phi_{j}.\end{aigned}}$

행렬 벡터 표기법에서,

${\displaystyle {\begin{aigned}{\frac {d\phi }{dt}&=-k(D-A)\phi \&=-kL\phi ,\ended{aigned}}}}$

어떤 것을 주는지

${\displaystyle {\frac {d\phi }{dt}+kL\phi =0.}$

이 방정식은 열 방정식과 동일한 형태를 취한다는 점에 유의하십시오. 여기서 매트릭스 -L은 라플라시안 연산자 $\nabla {\mathrm{}}^{}$ ${\$ 따라서 "그래프 라플라시안"을 대체한다.

이 미분 방정식의 해결책을 찾으려면 1차 행렬 미분 방정식을 해결하기 위한 표준 기법을 적용하십시오.That is, write ${\textstyle \phi }$ as a linear combination of eigenvectors ${\textstyle \mathbf {v} _{i}}$ of L (so that ${\textstyle L\mathbf {v} _{i}=\lambda _{i}\mathbf {v} _{i}}$) with time-dependent coefficients, ${\textstyle \phi$$(t)=\sum _{i}c_{i}(t)\mathbf {v} _{i}.$$}$

원래 식에 연결(L은 대칭 행렬이므로 단위 표준 고유 벡터 v ${}_{}$ ${\$은 직교함:

${\displaystyle {\begin}0={}&#{\frac {d\left(\sum _{i_{i}})({i}\right)}{dt}+kL\left(\sum _{i}c_{i}(t)\mathbf {v} _{i}\rigin_{i}\rig}\rig}\right)\i}\right)\right)\c}\i}\night)\c}\night)\\{}={}&\sum _{i}\왼쪽[{\frac {dc_{i}(t)}{dt}}\mathbf {v} _{i}+kc_{i}(t)L\mathbf {v} _{i}\ri}\right]\\\{}={}&\sum _{i}\left[{\frac {dc_{i}(t)}{dt}}\mathbf {v} _{i}+kc_{i}(t)\lambda _{i}\mathbf {v} _{i}\right]\\\Rightarrow 0={}&{\frac {dc_{i}(t)}{dt}}+k\lambda _{i}c_{i}(t),\\\end{aligned}}}$

누구의 해결책인가.

${\displaystyle c_{i}(t)=c_{i}(0)e^{-k\lambda _{i}t}.}$

앞에서 보듯이 L의 고유값 $\lambda {}_{}$ $i_{}$ ${\$는 음이 아닌 것으로서, 확산방정식의 용액이 평형에 근접한다는 것을 알 수 있는데, 이는 기하급수적으로 소멸하거나 일정하게 유지되기 때문이다.이는 또한 $given{}_{}$ $i_{}$ ${\$와 초기$$ 조건 $c{}_{}$ $i_{}$($){\textstyle c_{i}(0$이 주어진 경우 언제든지 솔루션을 찾을 수 있음을 보여준다.^[12]

${전체}_{}$ $초기$ 조건 $\varphi$ ($0$$){\$$textstyle i}$에 대해$$$$ 각 $i{}_{}$${\$$textstyle$ c_{i}(0$)$를$찾으려면$$\varphi$( 0$$) ${\textstyle$ $\$$pi (0)$를 단위 표준 고유 벡터 $v{\mathbf{}}_{}$ ${}_{}$ ${\$$i}}$에 투영하면 된다.

${\displaystyle c_{}}$ ${\displaystyle i_{}}$( ${\displaystyle 0}$)${\displaystyle }$= ${\displaystyle ⟨}$ ${\displaystyle \mathrm{\varphi }}$( 0${\displaystyle }$)${\displaystyle }$, v ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ ${\$v$} _{i}\right\angle$ $\}.$

이 접근방식은 구조화되지 않은 그리드의 정량적 열전달 모델링에 적용되었다.^[13][14]

비방향 그래프의 경우 $L$ ${\textstyle L}$이(가) 대칭이기 때문에, 스펙트럼 정리에 의해 그 고유 벡터는 모두 직교하기 때문에 이것이 작용한다.따라서 $L$ ${\textstyle L}$의 고유 벡터에 대한 투영은 단순히 초기 조건을 기하급수적으로 서로 독립적으로 붕괴하는 좌표 집합으로 직교 좌표 변환일 뿐이다$$.

평형행동

To understand ${\textstyle \lim _{t\to \infty }\phi (t)}$, the only terms ${\textstyle c_{i}(t)=c_{i}(0)e^{-k\lambda _{i}t}}$ that remain are those where ${\textstyle \lambda _{i}=0}$, since

${\displaystyle \lim _{t\to \ft }e^{-k\boda _{i}t}={\case}0,&{\cext{if}}\now\cH00\1,&\text{i}=0\end{case}}}}}}}}}}}$

즉, 시스템의 평형 상태는 $L$ ${\textstyle L}$의 커널에 의해 완전히 결정된다$.$

정의상 $\sum \underset{j}{}$ L $i_{}$ $\mathrm{j}{}_{}$= 0 ${\textstyle \sum _{j}L_{ij}=0},$벡터 $v{\mathbf{}}^{}$ ${\mathrm{}}^{}$ ${\$1}가$$ 커널 안에 있다.그래프에 $k$ ${\textstyle k}$ 분리된$$ 연결 구성요소가 있는 경우, 모든 $구성요소$의 이 벡터는 k$${\$textstyle k}$ 독립$$ $independent$= $0$ ${\textstyle \lambda =0}$ 고유$$ 벡터의 합으로 분할할 수 있으며, 여기서 각 연결된 구성요소는 커넥터의 요소에 있는 고유 벡터에 해당한다.d 성분과 0은 다른 곳에 있다.

$그$ 결과, N ${\textstyle N}$ 정점이$$ 있는 그래프에 대해$$ 지정된 초기 $조건$ c$$($0$) ${\textstyle$ c$(0)$

${\displaystyle \lim_{t\to \inflight }\phi(t)=\left\langle c(0),\mathbf {v^{1} \rigle \mathbf {v^{1}}}}}}$

어디에

${\displaystyle \mathbf {v^{1} ={\frac {1}{\sqrt{N}[1,1,\ldots,1}}$

element ${\textstyle \$$pi$ $}$의 각 요소 $\varphi {}_{}$ $j_{}$ ${\$ \$pi$ $_{j},$$$즉 그래프에 있는$$ 각 꼭지점 $j$ ${\textstyle j}$에 대해 다시 쓸 수 있다.

${\displaystyle \underset{}{림}}$ ${\displaystyle \underset{}{t}}$ → ${\displaystyle \underset{}{\infty \mathrm{}}{j}_{}}$ j${\displaystyle {}_{}}$(${\displaystyle t}$) = ${\displaystyle 1\frac{\mathrm{}}{}}$ ${\displaystyle \frac{N}{}\underset{i}{\overset{}{}}}$i = ${\displaystyle \underset{}{\overset{}{}}}$ N ${\displaystyle c_{}}$ ${\displaystyle \underset{}{\overset{}{}}{}_{}}$ ( ${\displaystyle 0}$)${\displaystyle \lim _{t\t$\to $\inflt }\phi _{j}(t)={{n}}}}}={i=1}c_{i}(0$

즉, 안정상태에서 $\varphi$ ${\textstyle \phi$} 값은 그래프의 각 정점에서 동일한 값으로$$ 수렴되는데, 이는 모든 정점에서의 초기 값의 평균이다.이것이 열 확산 방정식의 해결책이기 때문에, 이것은 직관적으로 완벽하게 이치에 맞는다.우리는 그 에너지가 서로 연결된 모든 요소들에 고르게 퍼져나갈 때까지 그래프의 이웃 요소들이 에너지를 교환할 것으로 기대한다.

그리드의 연산자 예제

이 GIF는 그래프 라플라시안 기법으로 해결된 확산의 진행과정을 보여준다.그래프는 그리드를 통해 생성되며, 그래프의 각 픽셀은 8개의 경계 픽셀에 연결된다.그 후 영상의 값은 이러한 연결을 통해 시간이 지남에 따라 이웃에게 부드럽게 확산된다.이 특별한 이미지는 이웃들에게 천천히 전해지는 세 가지 강점 가치로 시작한다.전체 체계는 결국 평형 상태에서 같은 값으로 안정된다.

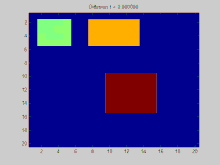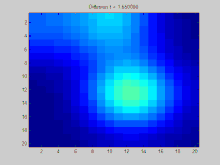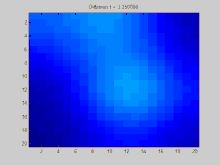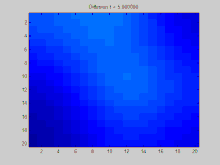
이 섹션에서는 그래프를 통해 시간에 따라 확산되는$$ 함수 ${\textstyle \phi }$의 예를 보여 준다.이 예제의 그래프는 그리드의 점이 8개의 이웃에 연결된 2D 이산 그리드에 생성된다.세 개의 초기 지점은 양의 값을 가지도록 지정되어 있는 반면, 그리드의 나머지 값은 0이다.시간이 지남에 따라 지수 붕괴는 이들 지점의 값을 전체 그리드에 걸쳐 균등하게 분배하는 작용을 한다.

이 애니메이션을 생성하는 데 사용된 전체 Matlab 소스 코드는 다음과 같다.초기 조건을 명시하고, 이러한 초기 조건을 라플라시안 매트릭스의 고유값에 투영하며, 이러한 예상 초기 조건의 지수적 붕괴를 시뮬레이션하는 과정을 보여준다.

N = 20; % 이미지 차원에 따른 픽셀 수 A = 0(N, N); % 이미지 보조 = 0(N * N, N * N); % 인접 행렬  이웃 8개를 사용하고 인접 행렬을 채우십시오. dx = [- 1, 0, 1, - 1, 1, - 1, 0, 1]; dy = [- 1, - 1, - 1, 0, 0, 1, 1, 1]; 을 위해 x = 1:N     을 위해 y = 1:N         색인을 달다 = (x - 1) * N + y;         을 위해 네 = 1:길이(dx)             뉴옥스 = x + dx(네);             뉴리의 = y + dy(네);             만일 뉴옥스 > 0 && 뉴옥스 <= N && 뉴리의 > 0 && 뉴리의 <= N                 지수2 = (뉴옥스 - 1) * N + 뉴리의;                 보조(색인을 달다, 지수2) = 1;             종지부를 찍다         종지부를 찍다     종지부를 찍다 종지부를 찍다  아래 %는 미분방정식에 대한 솔루션을 계산하는 핵심 코드다. 디그 = 검열하다(합계를 내다(보조, 2)); % 도 행렬 계산 L = 디그 - 보조; % 정도 및 인접 행렬의 측면에서 라플라시안 행렬 계산 [V, D] = 아이그(L); % 라플라시안 행렬의 고유값/벡터 계산 D = 검열하다(D);  % 초기 조건(큰 양의 값 몇 개를 주변에 배치) % 다른 모든 항목을 0으로 설정) C0 = 0(N, N); C0(2:5, 2:5) = 5; C0(10:15, 10:15) = 10; C0(2:5, 8:13) = 7; C0 = C0(:);  C0V = V'*C0; % 초기 조건을 좌표계로 변환 고유 벡터의 백분율 을 위해 t = 0:0.05:5     % 반복 시간 및 각 초기 구성 요소의 붕괴     피 = C0V .* 생략하다(- D * t); 각 성분에 대한 지수 붕괴 비율     피 = V * 피; % 고유 벡터 좌표계에서 원래 좌표계로 변환     피 = 모양을 바꾸다(피, N, N);     % 결과 표시 및 GIF 파일에 쓰기     imagesc(피);     축축([0, 10]);      칭호를 붙이다(단거리 경주('확산 t = %3f', t));     액자에 넣다 = 틀이 잡히다(1);     나는 = 틀2im(액자에 넣다);     [본을 뜨다, cm] = rgb2ind(나는, 256);     만일 t == 0         imwrite(본을 뜨다, cm, 'out.properties', 'gif', '루프카운트', 바 조로, 'DelayTime', 0.1);     다른         imwrite(본을 뜨다, cm, 'out.properties', 'gif', 'WriteMode', 'append', 'DelayTime', 0.1);     종지부를 찍다 종지부를 찍다 

이산 슈뢰딩거 연산자

$P{\displaystyle }$: ${\displaystyle V}$→ ${\displaystyle R}$ ${\displaystyle P\colon V\rightarrow R}$을(를) 그래프에 정의된 잠재적 함수가 되도록$$ 한다.참고로 P는 $\varphi {\displaystyle }$ ${\displaystyle \pi$}에 대각선으로 작용하는 곱셈 연산자로 간주할 수 있다.

$[\displaystyle (P\phi )(v)=P(v)\phi(v)]}$

$그{\displaystyle }$ 다음${\displaystyle }$H = ${\displaystyle \Delta }$+ P ${\displaystyle$ H$=\Delta +P}$는 이산 슈뢰딩거 연산자로, 연속 슈뢰딩거 연산자의 아날로그다.

정점에서 만나는 가장자리 수가 균일하게 경계되고, 전위가 경계가 되면 H는 경계가 되어 자기 성찰이 된다.

이 해밀턴인의 스펙트럼 특성은 스톤(Stone)의 정리로 연구할 수 있다; 이것은 양자와 부울 알헤브라스 사이의 이중성의 결과물이다.

일반 선반에서 운영자는 일반적으로 잠재력이 주기적인지 무작위인지에 따라 앤더슨 지역화 솔루션뿐만 아니라 여행파도 둘 다 가지고 있다.

이산 슈뢰딩거 연산자의 그린의 기능은 다음과 같은 분해 형식주의에 주어진다.

${\displaystyle G(v,w;\lambda )=\left\langle \delta _{v}\frac {1}{H-\lambda }}}}\right \delta _{w}\right\rangle }$

여기서 $\Delta {\displaystyle {}_{}}$ ${\displaystyle w_{}}$ ${\$는 그래프에서 크론커 델타 함수로 이해된다$$: $\Delta {\displaystyle {}_{}}$ ${\displaystyle w_{}}$(${\displaystyle v}$)${\displaystyle }$= ${\displaystyle {\Delta }_{}}$ w ${\displaystyle v_{}}$ ${\$ 즉, v=w와 0이면 1과 같다.

${\displaystyle \mathrm{고정}}$ $w{\displaystyle }${$$V {\$displaystyle w\in$ V$}$ $및{\displaystyle }$ $\$ {\$displaystyle \lambda }$ 복합$$ 번호인 경우, v의 함수로 간주되는 Green의 기능은 다음과 같은 고유한 솔루션이다.

${\displaystyle (H-\lambda )G(v,w;\lambda )=\delta _{w}(v).}$

ADE 분류

이산 라플라시안과 관련된 특정 방정식은 단순 레이싱된 Dynkin 다이어그램(모든 가장자리 다중성 1)에만 해법이 있으며 ADE 분류의 예다.특히, 동종 방정식에 대한 유일한 양성 해법은 다음과 같다.

${\displaystyle \Delta \phi =\phi ,}$

말로 하자면

"어떤 라벨의 2배는 인접 정점에 있는 라벨의 합이다."

확장(아핀) ADE Dynkin 다이어그램에 표시되며, 이 중 2개의 무한 패밀리(A와 D)와 3개의 예외(E)가 있다.그 결과 번호 매기는 스케일까지 고유하며, 가장 작은 값이 1로 설정되어 있으면 다른 숫자는 최대 6에 이르는 정수다.

일반 ADE 그래프는 다음과 같은 특성을 가진 양의 라벨링을 허용하는 유일한 그래프다.

두 배의 레이블에서 두 개의 레이블을 뺀 것은 인접한 정점에 있는 레이블의 합이다.

라플라크의 관점에서, 비균형 방정식에 대한 양성 해법은 다음과 같다.

${\displaystyle \Delta \phi =\phi -2.}$

결과 번호 매기는 고유하며("2"로 지정됨), 정수로 구성된다₈. E의 경우 범위는 58 ~ 270이며, 빠르면 1968년에 관측되었다.^[15]

참고 항목

• 스펙트럼 형상해석
• 전기망
• 이산 라플라시아인의 크로네커 합
• 이산 미적분학

참조

• T.Sunada, 이산 기하학적 분석, 순수 수학에서의 심포비아의 진행(ed. by P.엑너, J. P. 키팅, P. 쿠치먼트, T. 수나다, A.텔리야예프, 77(2008), 51-86

외부 링크

• 스펙트럼 갭에 대한 정의 및 적용