곱셈 알고리즘
Multiplication algorithm곱셈 알고리즘은 두 숫자를 곱하는 알고리즘(또는 방법)이다. 숫자의 크기에 따라 다른 알고리즘이 사용된다. 효율적인 곱셈 알고리즘은 십진법이 출현한 이후부터 존재해왔다.
격자법
격자법(또는 상자법)은 초등학교나 초등학교에서 학생들에게 자주 가르치는 다자리 곱셈의 입문법이다. 1990년대 후반부터 잉글랜드와 웨일스의 국민소학교 수학 커리큘럼의 표준 부분이었다.[1]
두 요인은 모두 수백, 수십, 단위 부품으로 분할되고 부품의 생산물은 비교적 단순한 곱셈 전용 단계에서 명시적으로 계산된 후, 이러한 기여도를 합산하여 별도의 추가 단계에서 최종 답을 제시한다.
예를 들어 계산 34 × 13은 그리드를 사용하여 계산할 수 있다.
300 40 90 + 12 ———— 442
| × | 30 | 4 |
|---|---|---|
| 10 | 300 | 40 |
| 3 | 90 | 12 |
그 다음, 442를 획득하기 위해 단일 합으로(오른쪽 참조) 또는 연속 합계를 형성하여(300 + 40) + (90 + 12) = 340 + 102 = 442를 얻는다.
이 계산 접근법(명시적인 그리드 배열은 반드시 그렇지는 않지만)은 부분적인 제품 알고리즘이라고도 한다. 그것의 본질은 단순 곱셈의 계산이며, 모든 덧셈은 최종 집합 단계에 맡겨진다.
격자법은 자릿수가 증가함에 따라 하위제품의 수가 번거로워지지만 어떤 크기의 요인에 대해서도 원칙적으로 적용할 수 있다. 그럼에도 불구하고, 이것은 여러 자리 수 승수의 개념을 도입하는 유용하게 명시적인 방법으로 보여진다; 그리고 대부분의 곱셈 계산이 계산기나 스프레드시트를 사용하여 수행되는 시대에, 그것은 실제로 일부 학생들에게 필요한 유일한 곱셈 알고리즘이 될 수도 있다.
긴 곱하기
위치수 체계를 사용한다면 학교에서 자연적으로 숫자를 곱하는 방법을 가르치게 되는데, 때로는 학년 곱하기라고 불리기도 하고, 때로는 표준 알고리즘이라고 불리기도 한다: 곱하기와 곱하기의 각 자릿수를 곱한 다음 적절하게 이동된 모든 결과를 합산한다. 한 자리 숫자에 대한 곱셈표를 암기해야 한다.
이것은 베이스 10에서 손으로 큰 숫자를 곱하기 위한 일반적인 알고리즘이다. 컴퓨터는 처음에 베이스 2에서 매우 유사한 시프트와 추가 알고리즘을 사용했지만, 현대의 프로세서는 보다 복잡한 하드웨어 실현의 가격으로 보다 효율적인 알고리즘을 사용하여 빠른 증식에 대한 회로를 최적화했다. 긴 곱셈을 하는 사람은 모든 제품을 종이에 적은 다음 그것들을 합할 것이다; 주판 사용자들은 각각의 제품이 계산되는 즉시 그 제품들을 합할 것이다.
예
이 예에서는 긴 곱셈을 사용하여 23,958,233(복수)에 5,830(복수)을 곱하고 결과(제품)에 대해 139,676,498,390에 도달한다.
23958233 × 5830 ——————————————— 00000000 ( = 23,958,233 × 0) 71874699 ( = 23,958,233 × 30) 191665864 ( = 23,958,233 × 800) + 119791165 ( = 23,958,233 × 5,000) ——————————————— 139676498390 ( = 139,676,498,390 )
아래 유사음식은 위의 곱셈 과정을 설명한다. 그것은 결국 결과가 되는 합계를 유지하기 위해 한 줄만 유지한다. '+=' 연산자는 콤팩트함을 위해 기존 값과 저장 작업(Java, C와 같은 언어에 해당)의 합을 나타내는 데 사용된다는 점에 유의하십시오.
곱셈을 하다(a[1..p], b[1..q], 밑의) // 색인 1에서 가장 오른쪽 자릿수를 포함하는 피연산자 상품 = [1..p+q] // 결과에 대한 공간 할당 을 위해 b_i = 1 로 q // b 단위의 모든 숫자에 대해 나르다 = 0 을 위해 a_i = 1 로 p // 의 모든 숫자에 대해 상품[a_i + b_i - 1] += 나르다 + a[a_i] * b[b_i] 나르다 = 상품[a_i + b_i - 1] / 밑의 상품[a_i + b_i - 1] = 상품[a_i + b_i - 1] 모드의 밑의 상품[b_i + p] = 나르다 // 마지막 숫자는 최종 운반에서 나온다. 돌아오다 상품 공간 복잡성 최적화
n을 베이스 D의 두 입력 번호에 있는 총 자릿수로 한다. 결과를 메모리에 저장해야 하는 경우 공간 복잡성은 사소한 ((n)이다. 그러나 특정 애플리케이션에서는 전체 결과를 메모리에 보관할 필요가 없으며 대신 결과의 자릿수는 계산되는 대로 스트리밍할 수 있다(예: 시스템 콘솔이나 파일로). 이러한 시나리오에서 긴 곱셈은 로그 공간 알고리즘, 즉 입력의 자릿수 로그(LOG n)에 비례하는 작업 공간만 필요한 알고리즘으로 쉽게 공식화할 수 있다는 장점이 있다. 이것은 스스로 곱하는 숫자의 이중 로그(로그 로그 N)이다. 피연산자 자체는 여전히 메모리에 저장되어야 하며, 피연산자의 space(n) 공간은 이 분석에서 고려되지 않는다.
이 방법은 이전 단계의 이월만 알고도 결과의 각 자릿수를 오른쪽에서 왼쪽으로 계산할 수 있다는 관측에 근거한 것이다. a와i b를i 피연산자의 i번째 자리, a와 b를 0으로 패딩하여 길이 n으로 하고, r은i 결과의 i번째 자리i, c는i r에 대해 생성된 캐리어가 되도록 한다(i=1은 오른쪽 가장자리임).
또는
간단한 귀납적 논거는 캐리어가 n을 절대 초과할 수 없고 r의i 총합이 D * n을 절대 초과할 수 없다는 것을 보여준다: 첫 번째 열로의 캐리어는 0이며, 다른 모든 열의 경우 컬럼에는 최대 n자리의 숫자가 있으며, 이전 열(유도 가설에 의한)에서 최대 n개의 캐리어가 있다. 합계는 최대 D * n이고, 다음 열까지의 운반은 최대 D * n / D 또는 n이다. 따라서 이 두 값은 모두 O(log n) 숫자로 저장할 수 있다.
유사 코드에서 로그 공간 알고리즘은 다음과 같다.
곱셈을 하다(a[1..p], b[1..q], 밑의) // 색인 1에서 가장 오른쪽 자릿수를 포함하는 피연산자 합계를 내다 = 0 을 위해 ri = 1 로 p + q - 1 // 결과의 각 자릿수에 대해 을 위해 bi = 맥스.(1, ri - p + 1) 로 분(ri, q) // 고려해야 할 b의 숫자 ai = ri − bi + 1 // 다음 "대칭"의 숫자 합계를 내다 = 합계를 내다 + (a[ai] * b[bi]) 상품[ri] = 합계를 내다 모드의 밑의 합계를 내다 = 마루를 깔다(합계를 내다 / 밑의) 상품[p+q] = 합계를 내다 모드의 밑의 // 결과의 마지막 자릿수는 마지막 운반에서 나온다. 돌아오다 상품 컴퓨터 사용량
일부 칩은 다양한 정수 및 부동 소수점 단어 크기에 대해 하드웨어 또는 마이크로코드로 긴 곱셈을 구현한다. 임의정밀 산술에서는 비교적 적은 숫자에 곱하기 위해 베이스가 2로w 설정된 긴 곱셈을 사용하는 것이 일반적이다.
이 방법을 사용하여 두 숫자를 n자리로 곱하려면 n자2 연산을 해야 한다. 좀 더 형식적으로: 숫자의 숫자의 자연 크기 측정법을 사용하여 긴 곱셈을 사용하여 두 개의 n자리 숫자를 곱하는 시간 복잡성은 θ(n2)이다.
소프트웨어에서 구현될 때 긴 곱셈 알고리즘은 추가 시 오버플로를 처리해야 하며, 비용이 많이 들 수 있다. 일반적인 해결책은 작은 베이스 b로 숫자를 표시하는 것이다. 예를 들어, 8b는 표현 가능한 기계 정수다. 그런 다음 오버플로가 발생하기 전에 몇 가지 추가 작업을 수행할 수 있다. 숫자가 너무 커지면 그 일부를 결과에 추가하거나, 나머지 부분을 다시 b보다 작은 숫자로 옮겨 매핑한다. 이 과정을 정상화라고 한다. 리처드 브렌트는 자신의 포트란 패키지인 MP에서 이런 접근법을 사용했다.[2]
격자 곱하기
격자, 즉 체에 의한 곱셈은 알고리즘적으로 긴 곱셈과 같다. 계산을 안내하고 모든 승수를 첨가물에서 분리하는 격자(종이에 그린 격자)를 준비해야 한다. 1202년 피보나찌의 리베르 아바시(Liber Abaci)에서 유럽에 소개되었다. 피보나찌는 그 수술을 정신적으로 묘사했는데, 그의 오른손과 왼손은 중간 계산을 운반하는 데 사용했다. 마트락처 나스흐는 이 16세기 책인 엄데툴 히삽에서 이 방법의 6가지 다른 변형을 제시했다. 오스만 제국 전역의 엔데룬 학교에서 널리 사용되었다.[3] 네이피어의 뼈, 즉 네이피어의 막대기도 그가 죽은 해인 1617년에 낸 것처럼 이 방법을 사용했다.
예시와 같이 격자 또는 체의 위와 오른쪽에 승수와 승수가 표기되어 있다. 2002년 '피보나치의 자유 아바시'의 저자 시글러가 언급한 레오나르도의 출처 중 하나인 무함마드 이븐 무사 알-크화리즈미의 '산술'에서 찾아볼 수 있다.[citation needed]
- 곱셈 단계 동안 격자는 각 행과 열에 해당하는 숫자의 두 자릿수 제품으로 채워진다. 즉, 왼쪽 상단 모서리에 수십 자릿수가 들어간다.
- 덧셈 단계에서 격자는 대각선으로 요약된다.
- 마지막으로 운반 단계가 필요한 경우, 긴 덧셈이나 곱셈처럼 10자리의 숫자를 옮겨 격자의 왼쪽과 아래쪽을 따라 표시된 답을 정상 형태로 변환한다.
예
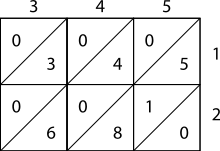
오른쪽의 그림은 격자 곱셈을 사용하여 345 × 12를 계산하는 방법을 보여준다. 보다 복잡한 예로서 아래 그림에 23,958,233의 계산에 5,830(복수)을 곱한 것을 고려해 보십시오. 결과는 139,676,498,390이다. 공지 23,958,233호는 격자 상단에, 5,830호는 우측에 있다. 제품들은 격자를 채우고 그 제품들의 합은 (대각선으로) 왼쪽과 아래쪽을 따라 있다. 그리고 그 총액은 그림과 같이 합산된다.
2 3 9 5 8 2 3 3 +---+---+---+---+---+---+---+---+- 1 / 1 / 4 / 2 / 4 / 1 / 1 / 1 / / / / / / / / / 5 01 / 0 / 5 / 5 / 5 / 0 / 0 / 5 / 5 +---+---+---+---+---+---+---+---+- 1 / 2 / 7 / 4 / 6 / 1 / 2 / 2 / / / / / / / / / 8 02 / 6 / 4 / 2 / 0 / 4 / 6 / 4 / 4 +---+---+---+---+---+---+---+---+- 0 / 0 / 2 / 1 / 2 / 0 / 0 / 0 / / / / / / / / / 3 17 / 6 / 9 / 7 / 5 / 4 / 6 / 9 / 9 +---+---+---+---+---+---+---+---+- 0 / 0 / 0 / 0 / 0 / 0 / 0 / 0 / / / / / / / / / 0 24 / 0 / 0 / 0 / 0 / 0 / 0 / 0 / 0 +---+---+---+---+---+---+---+---+- 26 15 13 18 17 13 09 00 | 01 002 0017 00024 000026 0000015 00000013 000000018 0000000017 00000000013 000000000009 0000000000000 ————————————— 139676498390 |
= 139,676,498,390 |
이진 또는 농민 곱하기
이항법은 농민 곱셈이라고도 하는데, 농민으로 분류되는 사람들에 의해 널리 사용되어 왔기 때문에 긴 곱셈에 필요한 곱셈표를 외우지 않았기 때문이다.[4][failed verification] 이 알고리즘은 고대 이집트에서 사용되고 있었다.[5][6] 종이와 연필이 없을 경우 빠르게 학습할 수 있고 암기가 필요 없으며 포커칩 등 토큰을 이용해 수행할 수 있는 것이 큰 장점이다. 단점은 긴 곱셈보다 더 많은 스텝을 밟기 때문에 큰 숫자로서는 감당하기 힘들 수 있다는 점이다.
설명
종이에 나머지 부분은 무시하고 승수를 반복해서 반으로 줄였을 때 얻은 숫자를 한 열에 적어라; 그 옆에 있는 열에는 승수를 두 배로 늘린다. 첫 번째 숫자의 마지막 숫자가 짝수인 각 행을 지우고, 두 번째 열에 나머지 숫자를 더하면 제품을 얻을 수 있다.
예
이 예는 농민 곱셈을 사용하여 11에 3을 곱하여 33의 결과를 얻는다.
십진수: 이진수: 11 3 1011 11 5 6 101 110 2 1211001 24 1 11000 - - - - - - - 33 100001
단계를 명시적으로 설명:
- 맨 위에 11과 3이 적혀 있다.
- 11은 절반(5.5), 3은 2배(6)이다. 부분적인 부분은 버려진다(5.5는 5가 된다).
- 5는 반감(2.5), 6은 2배(12)이다. 부분적인 부분은 버려진다(2.5는 2가 된다). 왼쪽(2)열의 수치는 짝수이므로 오른쪽(12)열의 그림은 폐기된다.
- 2는 반감(1) 12는 2배(24)이다.
- 검색되지 않은 모든 값은 합계가 3 + 6 + 24 = 33이다.
이 방법은 곱셈이 분배적이기 때문에 효과가 있다.
더 복잡한 예시, 앞의 예시(23,958,233 및 5,830)의 수치를 사용:
십진수: Binary: 583023958233101101100011010110110110010010110110012915 47916466 101101100011 10110110110010010110110010 1457 95832932 10110110001 101101101100100101101100100 72819166586410110110001011011011001001011011001000364383331728101101100101101101100100101101100100001827666634561011011010110110110010010110110010000091 1533326912 1011011 1011011011001001011011001000000 45 3066653824 101101 10110110110010010110110010000000 2261333076481011010110110110010010110110010000000011 12266615296 1011 1011011011001001011011001000000000 5 24533230592 101 10110110110010010110110010000000000 249066461184101011011011001001011011001000000000001 98132922368 1 1011011011001001011011001000000000000 ———————————— 1022143253354344244353353243222210110 (before carry) 139676498390 10000010000101010111100011100111010110
컴퓨터의 이진 곱하기
이것은 농민의 곱셈의 변형이다.
베이스 2에서 긴 곱셈은 거의 사소한 작업으로 줄어든다. 승수의 각 '1' 비트에 대해 승수를 적절한 양만큼 이동한 다음 이동한 값을 합하십시오. 일부 프로세서에서는 곱셈 지시보다 비트 이동과 추가 기능을 사용하는 것이 더 빠르며, 특히 곱셈이 작거나 항상 같은 경우에는 더욱 그러하다.
Shift and add
역사적으로 컴퓨터는 작은 정수를 곱하기 위해 "shift and add" 알고리즘을 사용했다. 염기 2 긴 곱셈과 염기 2 농민의 곱셈은 모두 이 같은 알고리즘으로 줄어든다. 베이스 2에서 승수의 한 자릿수를 곱하면 논리 AND 연산의 단순한 시리즈로 줄어든다. 각 부분 제품은 각 부분 제품이 계산되는 즉시 실행 합계에 추가된다. 현재 이용 가능한 대부분의 마이크로프로세서는 하드웨어 멀티플라이어 또는 마이크로코드의 다양한 정수 및 부동 소수점 크기에 대해 이것 또는 기타 유사한 알고리즘(부스 인코딩 등)을 구현한다.
현재 사용 가능한 프로세서에서 비트 와이즈 시프트 명령은 곱셈 명령보다 빠르며, 2의 힘으로 곱하기(좌회전)와 나누기(우회전)에 사용할 수 있다. 상수에 의한 곱셈과 상수에 의한 나누기는 일련의 교대조 및 덧셈 또는 뺄셈을 사용하여 실행할 수 있다. 예를 들어 비트 시프트와 추가만 사용하여 10을 곱하는 몇 가지 방법이 있다.
(x << 2> + x) < 1 # 여기서 10*x는 (x*2^2 + x)*2 (x < 3) + (x < 1) # 여기서 10*x는 x*2^3 + x*2로 계산된다.
어떤 경우에는 그러한 이동 및 추가 또는 차감 순서가 하드웨어 승수 및 특히 분할자를 능가할 것이다. 또는 ± 형식에 의한 분할은 종종 이렇게 짧은 시퀀스로 변환될 수 있다.
이러한 유형의 시퀀스는 "다중" 명령이 없는 컴퓨터에는 항상 사용되어야 하며,[7] 논리적으로 동등하기 때문에 x+x로 2*x의 계산으로 교대조정을 대체하는 경우 부동 소수점 번호로 확장하여 사용할 수도 있다.
4분의 1 제곱 곱하기
일부 출처가[8][9] 바빌로니아 수학(2000–1600 BC)에 귀속되는 바닥 함수와 관련된 다음과 같은 정체성을 채택하여 쿼터 사각형을 사용하여 두 양을 곱할 수 있다.
x+y와 x-y 중 하나가 홀수일 경우, 다른 것도 홀수여서 사각형이 1모드 4인 다음, 바닥이 4분의 1로 줄어들고, 뺄셈이 4분의 1로 줄어들며, 뺄셈이 4분의 1을 취소하고, 잔여물을 버리는 것은 바닥 기능이 없는 동일한 표현과 비교되는 어떤 차이도 일으키지 않는다. 아래는 0에서 18까지의 숫자에 대해 나머지가 버려진 쿼터 사각형의 조회표다. 이것은 9×9까지의 숫자의 곱셈을 허용한다.
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| ⌊n2/4⌋ | 0 | 0 | 1 | 2 | 4 | 6 | 9 | 12 | 16 | 20 | 25 | 30 | 36 | 42 | 49 | 56 | 64 | 72 | 81 |
예를 들어, 9에 3을 곱하려면 합과 차이가 각각 12와 6이라는 것을 관찰하십시오. 이 두 값을 모두 표에 올리면 36과 9가 나오고, 그 차이는 27이 되는데, 9와 3의 산물이다.
앙투안 보이신은 곱셈의 원조로 1817년 1부터 1000까지 4분의 1 정사각형 표를 발표했다. 1856년 사무엘 빨래방에 의해 1에서 10만까지의 4분의 1 정사각형 테이블이,[10] 1888년 조셉 블레이터에 의해 1에서 20만까지의 테이블이 발행되었다.[11]
쿼터 사각형 승수는 아날로그 컴퓨터에서 두 개의 아날로그 입력 신호의 산물인 아날로그 신호를 형성하기 위해 사용되었다. 이 애플리케이션에서는 작동 증폭기를 사용하여 두 입력 전압의 합과 차이를 형성한다. 이들 각각의 정사각형은 조각으로 된 선형 회로를 사용하여 근사치한다. 마지막으로 두 사각형의 차이는 또 다른 작동 증폭기를 사용하여 1/4의 인수로 형성되고 확장된다.
1980년에 에버렛 L. 존슨은 디지털 멀티플라이어로 쿼터 스퀘어 방식을 사용할 것을 제안했다.[12] 예를 들어 두 8비트 정수의 곱을 형성하기 위해 디지털 장치는 합과 차이를 형성하고, 정사각형 표에서 두 수량을 모두 올려다보고, 결과의 차이를 취하며, 오른쪽으로 두 비트를 이동하여 4로 나눈다. 8비트 정수의 경우 쿼터 사각형 표는 2-19=511 항목(전체 범위 0에 대해 하나의 항목).510개의 가능한 합계로, 0.209) 또는 2-19=511개 항목(차이의 부호를 시험하지 않는 2개 항목과 9비트 마스킹의 음의 차이에 사용), 각 항목은 16비트 폭이다(입력 값은 (0²/4)=0부터 (162²/4)=25까지).
쿼터 사각형 승수 기술은 하드웨어 승수를 지원하지 않는 8비트 시스템에도 혜택을 주었다. 찰스 퍼트니가 6502호에 이것을 구현했다.[13]
대용량 입력을 위한 빠른 곱셈 알고리즘
복합 곱셈 알고리즘
복잡한 곱셈은 보통 네 개의 곱셈과 두 개의 덧셈을 포함한다.
아니면
그러나 승수를 3으로 줄이는 방법이 있다.[14]
제품(a + bi) · (c + di)은 다음과 같은 방법으로 계산할 수 있다.
- k1 = c · (a + b)
- k2 = a · (d − c)
- k3 = b · (c + d)
- 실제1 부품 = k3 - k
- 상상의 부품 = k1 + k2.
이 알고리즘은 4개가 아닌 3개의 승수만을 사용하고, 2개가 아닌 5개의 추가나 소급만 사용한다. 만약 곱셈이 손으로 계산할 때처럼 3 더하기 또는 빼기보다 더 비싸다면, 속도의 증가가 있다. 현대의 컴퓨터에서는 곱셈과 덧셈이 거의 같은 시간이 걸릴 수 있기 때문에 속도 증가가 없을 수도 있다. 부동소수점 사용 시 정밀도가 다소 떨어질 수 있다는 점에서 절충이 있다.
빠른 푸리에 변환(FFT) (또는 모든 선형 변환)의 경우 복합 승수는 일정한 계수 c + di(FFT에서 트위들 인자라고 함)에 의해 이루어지며, 이 경우 추가 계수 중 두 가지(d-c 및 c+d)를 미리 계산할 수 있다. 따라서 3승 3패만 추가하면 된다.[15] 그러나 이러한 방식으로 곱셈을 더하기 위해 거래하는 것은 현대의 부동 소수점 단위에는 더 이상 이롭지 않을 수 있다.[16]
카라츠바 곱하기
컴퓨터 대수 체계나 비그넘 라이브러리처럼 수천 자리수 범위에서 숫자를 곱해야 하는 시스템의 경우 긴 곱셈이 너무 느리다. 이러한 시스템은 1960년(62년 출판)에 발견된 카라츠바 곱셈을 채용할 수 있다. 카라츠바 방법의 핵심은 두 자리 곱셈이 고전적으로 필요한 네 곱셈이 아니라 세 자리만 가지고 할 수 있다는 관측에 있다. 이것은 현재 분업-금융 알고리즘이라고 불리는 것의 한 예다. x1 m + x2 및 y1 m2 + y: 두 개의 기본 m 숫자를 곱한다고 가정합시다.
- 계산1 x · y1, 결과 F로 호출
- 계산2 x · y2, 결과 G를 호출한다.
- 계산(x1 + x2) · (y12 + y), 결과 H로 호출
- H - F - G를 계산하고 결과 K를 호출한다. 이 숫자는 x1 · y + x · y와21 같다2.
- 계산 F · m2 + K · m + G
기본 m 숫자의 이 세 가지 제품을 계산하기 위해, 우리는 재귀법을 효과적으로 사용하여 같은 기술을 다시 사용할 수 있다. 일단 수치가 계산되면 그것들을 함께 추가해야 하는데(4단계와 5단계) 이 작업은 n개 정도 걸린다.
카라츠바 곱셈은 O(nlog23) ≈ O(n1.585)의 시간 복잡성을 가지고 있어 이 방법이 긴 곱셈보다 현저하게 빠르다. 재귀의 오버헤드 때문에 카라츠바의 곱셈은 n의 작은 값에 대한 긴 곱셈보다 느리다. 따라서 일반적인 구현은 n의 작은 값에 대한 긴 곱셈으로 전환된다.
카라츠바의 알고리즘은 긴 곱셈보다 점증적으로 빠른 곱셈에 대한 최초의 알려진 알고리즘으로,[17] 따라서 빠른 곱셈 이론의 출발점으로 볼 수 있다.
1963년에 피터 언가르는 복잡한 곱셈 알고리즘의 비슷한 축소를 얻기 위해 m을 i로 설정할 것을 제안했다.[14] (a + b i) · (c + d i)를 곱하려면 다음 단계를 수행하십시오.
- 계산 b · d, 결과를 F라고 한다.
- a · c를 계산하고, 결과 G를 호출한다.
- 계산(a + b) · (c + d), 결과 H를 호출한다.
- 결과의 가상 부분은 K = H - F - G = a · d + b · c이다.
- 결과의 실제 부분은 G - F = a · c - b · d이다.
앞 절의 알고리즘과 마찬가지로, 여기에는 3개의 승수와 5개의 추가 또는 소급이 필요하다.
툼-쿡
또 다른 곱셈 방법은 Toom-Cook 또는 Toom-3이다. Toom-Cook 방법은 곱하기 위해 각 숫자를 여러 부분으로 나눈다. 툼-쿡 방법은 가라쓰바 방식의 일반화 중 하나이다. 텀-쿡의 3방향은 5가지 N배율 비용으로 3N배율을 할 수 있다. 이것은 9/5의 계수만큼 작동을 가속하는 반면, 가라쓰바 방법은 4/3까지 가속한다.
부품을 점점 더 많이 사용하면 재귀적 곱셈에 소비되는 시간을 더욱 줄일 수 있지만, 추가와 숫자 관리로 인한 오버헤드 또한 증가한다. 이러한 이유로 푸리에 변환 방법은 일반적으로 수천 개의 숫자를 가진 숫자의 경우 더 빠르고, 심지어 더 큰 숫자의 경우에는 점증적으로 더 빠르다.
푸리에 변환 방법

Strassen(1968)에 의한 기본적인 생각은 빠른 다항식 곱셈을 사용하여 빠른 정수 곱셈을 수행하는 것이다. 이 알고리즘은 쇤네게와 스트라센에 의해 1971년에 실용적이고 이론적인 보증이 제공되어 쇤네게-스트라센 알고리즘이 만들어졌다.[18] 자세한 내용은 다음과 같다. 우리는 아래에 설명된 과정 중에 오버플로를 유발하지 않는 가장 큰 정수 w를 선택한다. 그리고 나서 우리는 두 숫자를 다음과 같이 w비트의 m 그룹으로 나누었다.
이 숫자를 x의 다항식(다항식)으로 보고 여기서 x = 2를w 구하면
그러면 우리는 그렇게 말할 수 있다.
분명히 위의 설정은 두 다항식 a와 b의 다항식 곱셈에 의해 실현된다. 지금 중요한 단계는 다항식의 Fast Fourier 곱셈을 사용하여 위의 곱셈을 순진한 O(m2) 시간보다 빠르게 실현하는 것이다.
푸리에 변환의 모듈형 설정으로 유지하기 위해, 우리는 통합의 (2m) 루트를 가진 고리를 찾는다. 따라서 우리는 곱셈모듈로 N (따라서 Z/NZ 링에서)을 한다. 또한 N은 반드시 'wrap around'가 발생하지 않도록 선택되어야 하며, 본질적으로 감산 모듈로 N이 발생하지 않도록 해야 한다. 따라서 N의 선택이 결정적이다. 예를 들어, 다음과 같이 할 수 있다.
따라서 링 Z/NZ는 통합의 (2m)번째 뿌리 즉, 8을 가질 것이다. 또한k c < N을 확인할 수 있어 랩이 발생하지 않는다.
알고리즘은 θ(n log(n) log(n) log(n))의 시간 복잡성을 가지며, 10,000 ~ 40,000자리 이상의 숫자에 대해 실제로 사용된다. 2007년에 이것은 복잡한 숫자에 대한 푸리에 변환을 사용하여 n log(n) 2의Θ(log*(n)) 시간 복잡성을 주기 위해 Martin Fürer(총통의 알고리즘)[19]에 의해 개선되었다. 아닌디야 데, 찬단 사하, 피유시 쿠루르, 람프라사드 사파리시는[20] 같은 러닝타임을 달성한 2008년 모듈러 산수를 이용한 유사한 알고리즘을 부여했다. 위의 자료의 맥락에서, 이들 후자의 저자들이 달성한 것은 2 + 1보다3k 훨씬 적은 N을 찾아 Z/NZ가 (2m)의 통합의 뿌리를 가지도록 하는 것이다. 이것은 계산 속도를 높이고 시간 복잡성을 줄인다. 그러나 이러한 후자의 알고리즘은 실용적으로 큰 입력의 경우 Schönhage-Strassen보다 빠를 뿐이다.
2019년 3월 데이비드 하비와 조리스 반 데어 호이븐은 O(n log n) 곱셈 알고리즘을 발견했다고 발표했다.[21] 2021년 수학 연보에 실렸다.[22]
이산 푸리에 변환 대신 숫자-이론적 변환을 사용하면 부동 소수점 산술 대신 모듈식 산술을 사용하여 반올림 오류 문제를 방지할 수 있다. FFT가 작동할 수 있는 인수인자를 적용하기 위해서는 변환의 길이가 작은 소수점까지 인자가 되어야 하며 여기서 N은 필드 크기인 N - 1의 인자가 되어야 한다. 특히 k가 메르센 프라임인 갈루아 필드 GF(k2)를 사용한 계산에서는 2의 검정력에 해당하는 변환을 사용할 수 있다31. 예: k = 2 - 1은 최대 2의32 변환 크기를 지원한다.
하한
단일 프로세서에 두 개의 n비트 숫자를 곱하는 데 Ω(n)의 사소한 하한이 있다. 일치하는 알고리즘(기존 기계에, 튜링 등가 기계에 있음)이나 더 날카로운 하한이 알려져 있지 않다. 곱셈은 모든 prime p에 대해 AC0[p] 외부에 위치하며, 이는 제품을 계산할 수 있는 AND, OR, NOT 및p MOD 게이트를 사용하는 일정한 깊이, 다항식(또는 하위 표준) 크기의 회로가 없다는 것을 의미한다. 이는 MOD를q 지속적으로 심층적으로 축소하여 곱셈으로 바꾼 데서 비롯된다.[23] 곱셈 하한은 분기 프로그램의 일부 클래스에서도 알려져 있다.[24]
다항식 곱하기
위의 모든 곱셈 알고리즘도 다항식 곱셈으로 확장할 수 있다. 예를 들어 다항식 곱셈에[25] Strassen 알고리즘을 사용할 수 있다. 또는 Kronecker 대체 기법을 사용하여 다항식 곱셈의 문제를 단일 이항 곱셈으로 변환할 수 있다.[26]
대수적 공식의 곱셈을 허용하기 위해 긴 곱셈 방법을 일반화할 수 있다.
14ac - 3ab + 2 곱하기 ac - ab + 1
14ac -3ab 2 ac -ab 1 ———————————————————— 14a2c2 -3a2bc 2ac -14a2bc 3 a2b2 -2ab 14ac -3ab 2 ——————————————————————————————————————— 14a2c2 -17a2bc 16ac 3a2b2 -5ab +2 =======================================[27]
칼럼 기반 곱셈의 추가 예로서, 23 롱톤(t), 1200 중량(cwt), 2 쿼터(qtr)에 47을 곱하는 것을 고려한다. 이 예에서는 1 t = 20 cwt, 1 cwt = 4 qtr 등 아보오아르두푸아 측정법을 사용한다.
t cwt qtr 23 12 2 47 x ———————————————— 141 94 94 940 470 29 23 ———————————————— 1110 587 94 ———————————————— 1110 7 2 ================= Answer: 1110 ton 7 cwt 2 qtr
먼저 분기에 47을 곱하면 94가 첫 번째 작업 공간에 기록된다. 다음으로 cwt 12*47 = (2 + 10)*47을 곱하되, 부분적인 결과(94, 470)는 아직 합산하지 않는다. 마찬가지로 23에 47을 곱한다(141, 940). 쿼터 컬럼을 집계하고 그 결과를 두 번째 작업영역에 배치한다(이 경우 사소한 움직임). 94쿼터는 23 cwt, 2 qtr이니 2쿼터를 답안에 넣고 23쿼터를 왼쪽의 다음 칸에 넣으세요. 이제 587을 주는 cwt 컬럼에 3개의 항목을 추가한다. 이것은 29 t 7 cwt이니, 7은 답안에, 29는 왼쪽에 써라. 이제 톤수 기둥을 더해라. 조정할 수 없으니 결과는 그대로 베끼기만 한다.
구 영국 £sd 시스템과 같은 모든 전통적인 측정과 십진수 이외의 통화에 동일한 레이아웃과 방법을 사용할 수 있다.
참고 항목
- 이항 승수
- 분할 알고리즘
- 로그
- 멘탈 계산
- 프로스트하패레시스속
- 슬라이드 규칙
- 트라히텐베르크 제도
- 다항식 평가를 위한 호너 계획
- 나머지 번호 시스템 § 또 다른 빠른 곱셈 알고리즘을 위한 곱셈, 선형대수처럼 많은 연산이 순차적으로 수행될 때 특히 효율적임
- 다다승수
- 월리스 트리
참조
- ^ 개리 이슨, 2000년 2월 13일 BBC 뉴스, 학부모 학교로 돌아가다
Rob Eastaway, 왜 부모들은 오늘날 수학을 하지 못하는가, BBC 뉴스, 2010년 9월 10일 - ^ Brent, Richard P (March 1978). "A Fortran Multiple-Precision Arithmetic Package". ACM Transactions on Mathematical Software. 4: 57–70. CiteSeerX 10.1.1.117.8425. doi:10.1145/355769.355775. S2CID 8875817.
- ^ M. S. Burlbaw. L. M. Capraro, R. M. Corlu, M. A.&Han, S. (2010) 오스만 궁전 학교 엔데룬과 다재다능한 남자, 마트락처 나수. 한국수학교육학회지 D: 수학교육 연구. 14(1)페이지 19~31페이지.
- ^ Bogomolny, Alexander. "Peasant Multiplication". www.cut-the-knot.org. Retrieved 2017-11-04.
- ^ D. Wells (1987). The Penguin Dictionary of Curious and Interesting Numbers. Penguin Books. p. 44.
- ^ Cool Multiplication Math Trick, archived from the original on 2021-12-11, retrieved 2020-03-14
- ^ G의 "Novel Methods of 정수 곱셈과 나눗셈" 라이히본켄네루드
- ^ McFarland, David (2007), Quarter Tables Revisited: Earlier Tables, Division of Labor in Table Construction, and Later Implementations in Analog Computers, p. 1
- ^ Robson, Eleanor (2008). Mathematics in Ancient Iraq: A Social History. p. 227. ISBN 978-0691091822.
- ^ "Reviews", The Civil Engineer and Architect's Journal: 54–55, 1857.
- ^ Holmes, Neville (2003), "Multiplying with quarter squares", The Mathematical Gazette, 87 (509): 296–299, doi:10.1017/S0025557200172778, JSTOR 3621048, S2CID 125040256.
- ^ Everett L., Johnson (March 1980), "A Digital Quarter Square Multiplier", IEEE Transactions on Computers, Washington, DC, USA: IEEE Computer Society, vol. C-29, no. 3, pp. 258–261, doi:10.1109/TC.1980.1675558, ISSN 0018-9340, S2CID 24813486
- ^ Putney, Charles (Mar 1986), "Fastest 6502 Multiplication Yet", Apple Assembly Line, vol. 6, no. 6
- ^ a b Knuth, Donald E. (1988), The Art of Computer Programming volume 2: Seminumerical algorithms, Addison-Wesley, pp. 519, 706
- ^ P. Duhamel과 M. Verterli, Fast Fourier 변환: 자습서 검토 및 기술 상태" 웨이백 머신에 보관된 2014-05-29, 신호 처리 19, 페이지 259–299(1990), 섹션 4.1.
- ^ S. G. 존슨과 M. 프리고, "산술 연산이 적은 수정된 스플릿-라믹스 FFT," IEEE Trans. 신호 프로세스. 제55권, 페이지 111–119(2007), 섹션 IV.
- ^ D. Knuth, The Art of Computer Programming, vol. 2, sec 4.3.3 (1998년)
- ^ A. Shönhage와 V. Strassen, "Schnelle Multiquisation grozer Zahlen", Computing 7 (1971), 페이지 281–292.
- ^ 총통, M. (2007) 2007년 6월 11~13일 미국 캘리포니아주 샌디에이고에서 열린 제39회 컴퓨팅 이론 ACM 심포지엄의 진행 중 "빠른 정수 곱하기"
- ^ 아닌디야 데, 피유시 P 쿠루르, 찬단 사하, 람프라사드 사파리시 모듈식 산술을 사용한 빠른 정수 곱하기. 2008년 계산 이론 심포지엄
- ^ Hartnett, Kevin (2019-04-11). "Mathematicians Discover the Perfect Way to Multiply". Quanta Magazine. Retrieved 2019-05-03.
- ^ Harvey, David; van der Hoeven, Joris (2021). "Integer multiplication in time ". Annals of Mathematics. Second Series. 193 (2): 563–617. doi:10.4007/annals.2021.193.2.4. MR 4224716.
- ^ Sanjev Arora와 Boaz Barak, Computing Complex: A Modern Access, Cambridge University Press, 2009.
- ^ Farid Ablayev와 Marek Karpinski, 임의로 주문된 읽기-한 번 분기 프로그램, Information and Computing 186(2003, 78–89).
- ^ "Strassen algorithm for polynomial multiplication". Everything2.
- ^ von zur Gathen, Joachim; Gerhard, Jürgen (1999), Modern Computer Algebra, Cambridge University Press, pp. 243–244, ISBN 978-0-521-64176-0.
- ^ Castle, Frank (1900). Workshop Mathematics. London: MacMillan and Co. p. 74.
추가 읽기
- Warren Jr., Henry S. (2013). Hacker's Delight (2 ed.). Addison Wesley - Pearson Education, Inc. ISBN 978-0-321-84268-8.
- Savard, John J. G. (2018) [2006]. "Advanced Arithmetic Techniques". quadibloc. Archived from the original on 2018-07-03. Retrieved 2018-07-16.
- Johansson, Kenny (2008). Low Power and Low Complexity Shift-and-Add Based Computations (PDF) (Dissertation thesis). Linköping Studies in Science and Technology (1 ed.). Linköping, Sweden: Department of Electrical Engineering, Linköping University. ISBN 978-91-7393-836-5. ISSN 0345-7524. No. 1201. Archived (PDF) from the original on 2017-08-13. Retrieved 2021-08-23. (x+268 pages)