휠 인자화

이 기사는 위키피디아의 품질 기준을 충족시키기 위해 정리가 필요할 수 있다. 구체적인 문제는 다음과 같다. 컴퓨터 구현 알고리즘, 유사 코드, 추가 성능 분석, 계산 복잡성이 완전하지 않다. 가능한 경우 이 문서를 개선하는 데 도움을 주십시오. (2015년 2월) (이 템플리트 메시지를 제거하는 방법과 시기 알아보기)

휠 인자화는 정수 인자화를 위한 시험분할법의 개선이다.

시험분할방법은 제1정수(2, 3, 4, 5, ...)로 연속적으로 인자화할 숫자를 제1정수(2, 3, 4, 5, ...)로 나눈다. 바퀴 인자화의 경우, 일반적으로 처음 몇 개의 소수 소수 소수인 기초라고 불리는 작은 숫자의 리스트에서 시작하여 모든 기본 숫자와 일치하는 정수의 목록을 생성한다. 그런 다음, 인수할 숫자의 가장 작은 점을 찾기 위해, 기초와 바퀴에 있는 숫자로 연속적으로 나눈다.

{2, 3}을(를) 기준으로 이 방법은 재판분할에 필요한 수의 3분의 1 < 34%로 분할을 줄인다. 베이스가 클수록 이 비율은 더욱 감소한다. 예를 들어, 베이스가 {2, 3, 5}에서 8/30 < 27%로, 베이스가 {2, 3, 5, 7}에서 48/210 < 23%로 감소한다.

대표적인 예

처음 소수 소수 소수 소수 소수점 {2, 3, 5}의 주어진 기준으로 휠의 "첫 번째 턴"은 다음과 같이 구성된다.

7, 11, 13, 17, 19, 23, 29, 31.

두 번째 턴은 첫 번째 턴의 숫자에 기초의 산물인 30을 더해서 얻는다. 세 번째 턴은 두 번째 턴에 30을 더하면 얻어진다.

이 방법을 실행하기 위해서는 바퀴의 연속적인 두 요소 사이의 증분, 즉 다음과 같이 말할 수 있다.

inc = [4, 2, 4, 2, 4, 6, 6, 6],

한 바퀴씩 돌고도 변하지 않다

다음에 제시된 구현은 n이 k로 균등하게 분할되는지 여부를 시험하는 보조 함수 div(n, k)를 사용하며, 이 경우 true를 반환하며, 그렇지 않으면 거짓이다. 이 구현에서, 인수할 숫자는 n이며, 프로그램은 n의 가장 작은 구분자를 반환하며, 소수점인 경우에는 n을 반환한다.

div(n, 2) = true이면 2를 반환하고, div(n, 3) = true이면 3을 반환하고, div(n, 5) = true이면 5 k := 7을 반환하고, div(n, k) = true이면 k := k + inc[i]를 반환하고, "8"이면 k : = i + 1을 반환한다. 

정수의 완전한 인자화를 얻기 위해, 초기에는 휠을 다시 시작하지 않고 계산을 계속할 수 있다. 이것은 완전한 요소화를 위해 다음과 같은 프로그램으로 이어지고, 여기서 함수 "add"는 반드시 리스트가 되어야 하는 두 번째 인수의 끝에 첫 번째 인수를 추가한다.

factors := [ ] while div(n, 2) = true do     factors := add(2, factors)     n := n / 2 while div(n, 3) = true do     factors := add(3, factors)     n := n / 3 while div(n, 5) = true do     factors := add(5, factors)     n := n / 5 k := 7; i := 0 while k * k ≤ n do if div(n, k) = true then          add(k, factors)         n := n / k else k := k + inc[i] i < 8이면 i := i + 1 다른 i := 1 n > 1이면 반환 인자를 더한다(n, 요인). 

또 다른 발표

휠 인자화는 간단한 수학 공식과 첫 번째 소수보다 훨씬 작은 리스트에서 대부분의 소수 목록을 생성하는 데 사용된다. 이 목록은 시험 분할 또는 체에 사용될 수 있다. 이 목록에 있는 모든 숫자가 소수인 것은 아니기 때문에, 그렇게 하는 것은 비효율적인 중복 운영을 도입한다. 그러나 발전기 자체는 순수한 소수 목록을 유지하는 것에 비해 기억력이 거의 필요하지 않다. 초기 소수 목록은 목록의 나머지 부분을 생성하기 위한 알고리즘의 완전한 매개변수를 구성한다. 이러한 발전기를 바퀴라고 한다. 각 휠은 무한히 많은 수의 목록을 생성할 수 있지만, 특정 지점을 지나면 숫자가 대부분 소수점 이하가 된다.

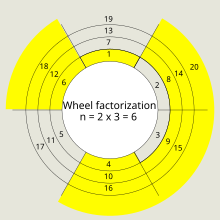
이 방법은 보다 정확한 휠을 생성하기 위해 소수 휠 체로 재귀적으로 적용할 수 있다. 휠 팩터화, 휠 팩터화를 사용하는 체, 휠 체에 관한 많은 결정적인 작업은 폴^[1][2][3][4] 프리처드가 일련의 다른 알고리즘을 형성하는 과정에서 수행했다. 인자화 휠의 사용을 시각화하기 위해, 인접한 도표와 같이 원을 중심으로 자연수를 쓰는 것으로 시작할 수 있다. 대변인의 수는 소수 대변인에 축적되는 경향을 가질 수 있도록 선택된다.

샘플 그래픽 절차

1. 인자화 휠의 기초를 형성하기 위해 처음 몇 개의 소수 소수 소수점을 찾아라. 이러한 휠은 이전의 소형 인자화 휠 적용 또는 Eratosthenes의 체를 사용하여 신속하게 발견함으로써 알려지거나 결정된다.
2. 기본 소수점 수를 함께 곱하여 인자화 휠의 둘레에 해당하는 n 결과를 제공한다.
3. 숫자 1부터 n까지 원을 그리며 써라. 이것은 바퀴의 한 바퀴 회전을 나타내는 가장 안쪽의 원이 될 것이다.
4. 가장 안쪽 원의 숫자 1에서 n까지, 2단계에서 적용되는 것처럼 1단계부터 베이스 프리임의 모든 배수를 스트라이크한다. 이 복합 번호 제거는 체(Ceet of Eratosthenes)와 같은 체(Ceet)를 사용하거나 더 작은 인자화 휠을 적용하여 수행할 수 있다.
5. x를 지금까지 쓰여진 원의 수로 가져가면 xn + 1 ~ xn + n을 가장 안쪽 원 주변의 동심원 안에 계속 쓰면서, xn + 1이 (x - 1)n + 1과 같은 위치에 있게 된다.
6. 가장 큰 회전 원이 가장 큰 숫자에 걸쳐 원시성을 테스트할 때까지 5단계를 반복하십시오.
7. 숫자 1을 잘라내라.
8. 1단계에서 찾은 대로 가장 안쪽 원(1번 원)에서 가장 안쪽 원(원)의 소수점을 제거하지 않고 모든 바깥 원(원)에서 2단계에 적용된 소수점 대변을 잘라내십시오.
9. 8단계에서 베이스 프리타임의 스포크를 타격하는 것과 같은 방법으로 4단계에서 1번 내부 서클에서 타격된 모든 소수 배수의 스포크를 타격한다.
10. 바퀴에 남아 있는 숫자는 대부분 소수(일괄적으로 "상대적" 소수)이다. Eratosthenes의 체 또는 더 큰 인자화 휠의 추가 적용과 같은 다른 방법을 사용하여 나머지 비임상 시간을 제거하십시오.

예

1. 처음 두 개의 소수: 2와 3을 찾아라.

2. n = 2 × 3 = 6

3.

 1  2  3  4  5  6 

4. 2와 3의 스트라이크오프 요인 4와 6은 2의 요인으로, 6은 3의 유일한 요인으로 이미 영향을 받고 있다.

 1  2  3  4  5  6 

5. x = 1.
xn + 1 = 1 · 6 + 1 = 7.
(x + 1)n = (1 + 1) · 6 = 12.
7을 1로 정렬하고 7을 7에서 12로 쓰시오.

 1  2  3  4  5  6  7  8  9 10 11 12 

6. x = 2.
xn + 1 = 2 · 6 + 1 = 13.
(x + 1)n = (2 + 1) · 6 = 18.
13부터 18까지 쓰세요.
다음 몇 줄에 대해 반복하십시오.

 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 

7번과 8. 체빙

 1  2  3  4  5  6  7  8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 

9. 체빙

 1  2  3  4  5  6  7  8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 

10. 결과 목록에는 5인² 25의 비우량 번호가 포함되어 있다. 체 등의 다른 방법을 사용하여 제거하여 도착하게 한다.

2 3 5 7 11 13 17 19 23 29 

다음 5개 휠 사이클의 소수점 이하를 정확히 사용하고 그 소수점 이하(그리고 소수점 이하만 해당)의 배수를 결과 목록에서 제거함으로써, 기본 소수점 2, 3, 5의 인수 휠에 대해 4단계에 따라 기본 휠을 확보했다는 점에 유의하십시오. 이 휠은 이전 2/3 인수 휠보다 1개 앞선 휠입니다. 그 다음에 이어지는 7 사이클의 프라임을 사용하여 10단계를 실행하고 10단계의 결과 목록에서 7의 배수를 제거할 수 있다(이 경우 일부 "상대적" 프리마임을 제거하고 모든 연속적인 경우(즉, 일부 완전하지 않은 프리마임)는 다음 추가 고급 휠을 확보하여 단계를 반복적으로 반복할 수 있다.s 연속적으로 더 큰 바퀴를 얻기 위해 필요한 만큼.

분석 및 컴퓨터 구현

형식적으로 이 방법은 다음과 같은 통찰력을 이용한다. 첫째, 기본 소수 집합이 그 (무한) 복사 집합과 결합한 것은 소수 집합의 상위 집합이다. 둘째, 무한의 조합 집합은 2와 기본 집합 제품 사이의 조합 집합에 이르기까지 쉽게 열거할 수 있다. (참고 1은 특별한 취급이 필요하다.)

위의 예에서 볼 수 있듯이, 4단계부터 10단계까지 위의 반복적 적용의 결과는 원하는 체이빙 범위(절단할 수 있는 범위)에 걸쳐 있는 휠 목록이 될 수 있으며, 그 결과 목록은 마지막으로 사용한 베이스 프리타임 이후의 프리타임의 배수만 포함한다.

휠이 원하는 체이빙 범위의 상한에 도달하면 추가 휠 생성을 중지하고 해당 휠의 정보를 사용하여 마지막 휠 목록에서 나머지 합성 숫자를 도태할 수 있지만 중복 도태를 방지하기 위해 휠 고유의 간격 패턴을 사용한다. 일부 최적화(다음 섹션에서 입증될) 합성수의 반복적인 도태가 없다는 사실에 기초하여 (각 나머지 합성물은 정확히 한 번 도태될 것이다.)를 기초로 할 수 있다. 또는 원하는 체 범위의 제곱근까지 자른 값을 사용하여 잘린 휠 목록을 계속 생성할 수 있으며, 이 경우 휠에 남아 있는 모든 숫자 표시가 주기가 된다. 그러나 이 방법은 합성수를 두 번 이상 도태하지 않을 정도로 효율적이지만 노마 외부에서 많은 시간을 손실한다.휠 스위프를 연속적으로 처리할 때 훨씬 더 오래 걸릴 수 있도록 도태 작업을 고려했다. 인자화 바퀴에 의한 복합수의 제거는 다음과 같은 것에 근거한다: 숫자 k > n을 주어 k mod n과 n이 상대적으로 prime이 아니라면 k가 prime이 아니라는 것을 우리는 알고 있다. 그로부터, 휠 체가 제거하는 수의 분율을 1 - phi (n) / n으로 결정할 수 있다(모든 것을 물리적으로 차단할 필요는 없지만, 더 작은 휠을 더 큰 휠로 복사하는 작업에서 다수가 자동으로 도태될 수 있다). 이것이 체의 효율이기도 하다.

라고 알려져 있다.

${\displaystyle \lim \inf {\frac {\varphi (n)}{n}\log n=e^{-\required }\sim 0.56145948,}$

여기서 γ은 오일러의 상수다.^[5] 따라서 phi(n) / n은 n이 무한대로 증가함에 따라 천천히 0으로 가고 무한히 큰 n에 대해서는 이 효율이 매우 느리게 100%로 상승함을 알 수 있다. phi의 속성에서 보면 x보다 작은 체가 = p 2.. . . < < ${\displaystyle n=p_{1}p_{2}...$라는 것을 쉽게 알 수 있다.$p_{i}<x}$ 및 $n{\displaystyle }$ ${\displaystyle p_{}}$ ${\displaystyle {}_{}}$+ ${\displaystyle 1}$ ${\displaystyle {}_{}}$ x ${\displaystyle np_{i+1}\geq x}($즉, 마지막 바퀴가 지나갈 때 휠 생성이 중지되거나 체이빙 범위에 가장 높은 숫자를 포함하기에 충분한 원주가 있을 때 휠 생성이 중지될 수 있다).

컴퓨터에서 최대한 활용하기 위해 n보다 작고 비교적 소수인 숫자를 집합으로 하고 싶다. 몇 개의 관측치를 사용하여 세트를 쉽게 생성할 수 있다.

1. S ${\displaystyle {1\mathrm{}}_{}}$=${\displaystyle }${ ${\displaystyle 1}$ ${\displaystyle \}}$ ${\displaystyle S_{1}=\{1\}$ 로 시작하십시오$.$ 이 설정은 $n{\displaystyle }$= 1 ${\displaystyle n=1}$에 대한 설정이며, ${\displaystyle 2}$는 첫 번째 프라이밍으로 설정된다. 이 초기 세트는 바퀴의 둘레가 1이기 때문에 두 개에서 시작하는 모든 숫자가 "상대적" 프리타임으로 포함됨을 의미한다.
2. Following sets are ${\displaystyle S_{2}=\{1\}}$ which means that it starts at 3 for all odd numbers with the factors of 2 eliminated (circumference of 2), ${\displaystyle S_{6}=\{1,5\}}$ has the factors of 2 and 3 eliminated (circumference of 6) as for the initial base wheel in the example above and 등등
3. ${\displaystyle {Sn}_{}}$+ ${\displaystyle k}$ ${\displaystyle S_{n}+k}$을(를) $S{\displaystyle {}_{}}$ ${\displaystyle n_{}}$ ${\$의 각 요소에 k가 추가된 세트가 되도록$$ 한다$.$
4. 그러면 ${\displaystyle {{\mathrm{Sn}}_{}}_{}}$ ${\displaystyle {p_{}}_{}}$ i${\displaystyle {{}_{}}_{}}$+ 1${\displaystyle {{}_{}}_{}}$= ${\displaystyle {{\mathrm{F}}_{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {i_{}}_{}}$+ 1${\displaystyle {{}_{}}_{}}$[ ${\displaystyle S_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ S ${\displaystyle n_{}}$+ n ${\displaystyle \cup }$ ${\displaystyle S_{}}$ ${\displaystyle {}_{}}$+ ${\displaystyle 2}$ ${\displaystyle \mathrm{n}}$ ${\displaystyle \cup }$. .${\displaystyle \cup }$ ${\displaystyle {}_{}}$ n${\displaystyle {}_{}}$+ n (${\displaystyle p}$ ${\displaystyle i_{}}$+ ${\displaystyle 1_{}}$- ${\displaystyle 1}$) ${\displaystyle ]}$ ${\displaystyle S_{np_{i+1$}:1$}}=$$F_{p_{i+1}}[$$S_{n}\cup S_{n}+n\cup S_{n}+{n}+2n\cup ...$$\cup S_{n}+n(p_{i+1}-1)]}$ 여기서$$ ${\displaystyle F_{}}$ x ${\$은 x의 모든 배수를 제거하는 작업을 나타낸다$$.
5. 알고리즘이 후속 집합에 더 이상 포함되지 않는 모든 제거된 베이스 프리타임 기록을 유지해야 하지만 > 2 ${\displaystyle n>2}$을(를) 별도로 계산할 필요가 없는 경우$$ 1 ${\displaystyle {및}_{}}$ ${\displaystyle p_{}}$ $i{\displaystyle {}_{}}$+ ${\displaystyle 1_{}}$ ${\$ $p_{n}$의 두 개 $중$에서 가장 작은 값이 된다$$.
6. 원주 n > 2가 $n{\displaystyle }$/ 2 ${\displaystyle n/2$}을$($를$)$ 중심으로 대칭되는 모든 세트로 스토리지 요구사항 감소 다음 알고리즘은 이 사실을 사용하지 않지만, 각 집합의 연속된 숫자 사이의 간격이 중간점을 중심으로 대칭적이라는 사실에 기초한다.

참고 항목

• 순다람의 체
• 앳킨의 체
• 체 이론

참조

외부 링크

• 휠 인자화
• Paul Pricchard에 의한 증분 소수점 Sieves 개선