하디-바인베르크 원리

이 문서에는 일반 참조 목록이 포함되어 있지만 해당 인라인 인용이 충분하지 않습니다. 좀 더 정확한 인용문을 소개하여 이 기사를 개선하는 데 도움을 주시기 바랍니다. (2020년 4월) (이 템플릿 메시지를 제거하는 방법과 시기에 대해 알아보십시오.)

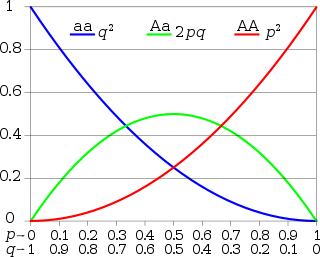
집단 유전학에서 하디-바인베르크 평형, 모델, 정리 또는 법칙으로도 알려진 하디-바인베르크 원리는 다른 진화적 영향이 없을 때 집단의 대립유전자 및 유전자형 빈도가 세대 간 일정하게 유지된다는 것을 말합니다. 이러한 영향에는 유전적 드리프트, 짝 선택, 다양한 교배, 자연 선택, 성적 선택, 돌연변이, 유전자 흐름, 감수분열 드라이브, 유전적 히치하이킹, 개체군 병목 현상, 창시자 효과, 근친 교배 및 외래종 우울증이 포함됩니다.

각각 빈도 (A) = p 및 (a) = q를 갖는 A 및 a로 표시된 2개의 대립유전자를 갖는 단일 유전자좌의 가장 간단한 경우, 무작위 교배 하에서 예상되는 유전자형 빈도는 AA 동형 접합체의 경우 (AA) = p, aa 동형 접합체의 경우 (Aa) = q, 이형 접합체의 경우 (Aa) = 2pq입니다. 선택, 돌연변이, 유전적 드리프트 또는 기타 힘이 없는 경우 대립유전자 빈도 p와 q는 세대 간에 일정하므로 평형에 도달합니다.

이 원리는 수학적으로 처음 증명한 G. H. Hardy와 Wilhelm Weinberg의 이름을 따서 명명되었습니다. 하디의 논문은 지배적인 대립유전자가^[1] 자동적으로 빈도가 증가하는 경향이 있을 것이라는 견해(강의에서 잘못 해석된 질문에 기초한 견해)를 밝히는 데 초점을 맞췄습니다. 오늘날, 하디-바인버그 유전자형 빈도에 대한 테스트는 주로 집단 계층화 및 다른 형태의 비-랜덤 교배에 대한 테스트에 사용됩니다.

파생

각 유기체가 동일한 빈도로 수컷과 암컷의 배우자를 생성하고 각 유전자 유전자좌에 두 개의 대립유전자를 갖는 단일성 이배체 집단을 생각해 보십시오. 우리는 개체 수가 너무 많아서 무한대로 취급될 수 있다고 가정합니다. 생물은 생식세포의 무작위 결합("유전자 풀" 집단 모델)에 의해 번식합니다. 이 모집단의 유전자좌에는 각각 초기 주파수 f(A) = p 및 f(a) = q에서 발생하는 두 개의 대립유전자 A 및 a가 있습니다. 각 세대의 대립유전자 빈도는 동형 접합체 및 이형 접합체 유전자형의 예상 기여도에 따라 동일한 세대의 각 유전자형의 대립유전자를 함께 풀링하여 얻어지는데, 각각 1 및 1/2입니다.

${\displaystyle f_{t}({\text})A})=f_{t}({\text{AA}})+{\tfrac {1}{2}}f_{t}({\text{Aa}})}$

(1)

${\displaystyle f_{t}({\text{a}})=f_{t}({\text{aa}})+{\tfrac {1}{2}}f_{t}({\text{Aa}})}$

(2)

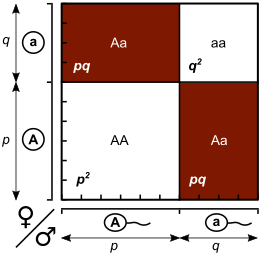
다음 세대의 유전자형을 형성하는 다양한 방법은 Punnet Square에서 보여질 수 있으며, 여기서 각 유전자형의 비율은 현재 세대의 행 및 열 대립 유전자 빈도의 곱과 같습니다.

표 1: 하디-와인버그의 퍼넷 제곱

		여성
		A(p)	a (q)
남성	A(p)	AA(p2)	Aa(pq)
	a (q)	Aa(qp)	aa(q2)

유전자형 빈도는 1로 합해야 하므로 항목의 합은 p + 2pq + q = 1입니다.

p + q = 1로서 (p + q) = p + 2pq + q = 1의 이항 전개가 동일한 관계를 제공한다는 점에 다시 주목합니다.

Punnet 제곱 또는 이항 전개의 요소를 합하면 단일 세대 후 자손 사이에서 예상되는 유전자형 비율을 얻을 수 있습니다.

${\displaystyle f_{1}({\text})AA}})=p^{2}=f_{0}({\text{A})^{2}}$

(3)

${\displaystyle f_{1}({\text{Aa}})=pq+qp=2pq=2f_{0}({\text{A})f_{0}({\text{a}}}$

(4)

${\displaystyle f_{1}({\text{aa}})=q^{2}=f_{0}({\text{a}})^{2}}$

(5)

이러한 주파수는 하디-바인베르크 평형을 정의합니다. 1세대 이후의 유전자형 빈도는 f(AA) ≠ f(AA)와 같이 초기 세대의 유전자형 빈도와 동일할 필요는 없습니다. 그러나 모든 미래 시간에 대한 유전자형 주파수는 t > 1에 대한 f(AA) = f(AA)와 같은 하디-와인버그 주파수와 동일합니다. 다음 세대의 유전자형 주파수는 식 (1) 및 (2)에 의해 계산된 대로 초기 세대에서 보존되는 현재 세대의 대립 유전자 주파수에만 의존하기 때문에 다음과 같습니다.

${\displaystyle {\begin{aligned}f_{1}({\text})A})&=f_{1}({\text{AA}})+{\tfrac {1}{2}}f_{1}({\text{Aa}})=p^{2}+pq=p(p+q)=p=f_{0}({\text{A}})\\f_{1}({\text{a}})&=f_{1}({\text{aa}})+{\tfrac {1}{2}}f_{1}({\text{Aa}})=q^{2}+pq=q(p+q)=q=f_{0}({\text{a}})\end{aligned}}}$

개체의 무작위 교배에 의해 번식하는 더 일반적인 경우 [생물은 수컷 또는 암컷이다]의 경우, 각 성별에서 각 모체 유전자형(AA, Aa 및 Aa) 사이의 가능한 9개의 교배에서 유전자형 빈도를 계산하고 이러한 교배의 예상 유전자형 기여도로 가중치를 부여해야 합니다.^[2] 마찬가지로 6가지 고유한 이배체-이배체 조합을 고려합니다.

${\displaystyle \left[({\text{)]AA}},{\text{AA}),({\text{AA}},{\text{Aa}},({\text{AA}},{\text{aa}},({\text{Aa}},({\text{Aa}},({\text{aa}}),({\text{aaa}},({\text{aa}}),({\text{aaa})\right]}$

그리고 각각의 Punnet square를 구축하여 다음 세대의 유전자형에 대한 기여를 계산합니다. 이러한 기여도는 k = 3인 다항 분포를 따르는 각 이배체- dip체 조합의 확률에 따라 가중치가 부여됩니다. 예를 들어, 짝짓기 조합(AA,aa)의 확률은 2f(AA)f(aa)이며, Aa 유전자형([0,1,0])만을 초래할 수 있습니다. 전체적으로 결과 유전자형 빈도는 다음과 같이 계산됩니다.

${\displaystyle {\begin{aligned}&\left[f_{t+1}({\text})AA}}),f_{t+1}({\text{Aa}}),f_{t+1}({\text{aa}})\right]=\\&\qquad =f_{t}({\text{AA})f_{t}({\text{AA}})\left[1,0,0\right]+2f_{t}({\text{AA}})f_{t}({\text{Aa}})\left[{\tfrac {1}{2}},{\tfrac {1}{2}},0\right]+2f_{t}({\text{AA}})f_{t}({\text{aa}})\left[0,1,0\right]\\&\qquad \qquad +f_{t}({\text{Aa}})f_{t}({\text{Aa}})\left[{\tfrac {1}{4}},{\tfrac {1}{2}},{\tfrac {1}{4}}\right]+2f_{t}({\text{Aa}})f_{t}({\text{aa}})\left[0,{\tfrac {1}{2}},{\tfrac {1}{2}}\right]+f_{t}({\text{aa}})f_{t}({\text{aa}})\left[0,0,1\right]\\&\qquad =\left[\left(f_{t}({\text{AA}})+{\tfrac {1}{2}}f_{t}({\text{Aa}})\right)^{2},2\left(f_{t}({\text{AA}})+{\tfrac {1}{2}}f_{t}({\text{Aa}})\right)\left(f_{t}({\text{aa}})+{\tfrac {1}{2}}f_{t}({\text{Aa}})\right),\left(f_{t}({\text{aa}})+{\tfrac {1}{2}}f_{t}({\text{Aa}})\right)^{2}\right]\\&\qquad =\left[f_{t}({\text{A})^{2},2f_{t}({\text{A}})f_{t}({\text{a}}),f_{t}({\text{a}})^{2}\right]\end{aligned}}}$

이전과 마찬가지로 시간 t + 1에서의 대립유전자 주파수는 시간 t에서의 대립유전자 주파수와 같으므로 시간에 일정하다는 것을 보여줄 수 있습니다. 마찬가지로 유전자형 빈도는 대립유전자 빈도에만 의존하므로 시간 t = 1 이후에도 시간이 일정합니다.

단독성 또는 난독성 유기체에서 대립유전자 또는 유전자형 비율이 처음에는 성별 중 하나에서 동일하지 않은 경우 한 세대의 무작위 교배 후에 일정한 비율이 얻어짐을 보여줄 수 있습니다. 난치성 유기체가 이종 생식이고 유전자 유전자좌가 X 염색체에 위치하는 경우, 대립 유전자 빈도가 처음에는 두 성별(예: 인간의 경우와 같이 XX 암컷과 XY 수컷)에서 동일하지 않은 경우, 이전 세대의 동종 생식 성별에서 이종 생식 성별 '추격'(a)의 ''(a), 두 초기 주파수의 가중 평균에서 평형에 도달할 때까지.

하디-바인베르크 평형으로부터의 편차

하디-바인베르크 평형의 기초가 되는 7가지 가정은 다음과 같습니다.^[3]

• 유기체는 이배체입니다.
• 성적 생식만이 일어나는 것입니다.
• 세대가 겹치지 않습니다.
• 짝짓기는 무작위입니다.
• 인구 규모가 무한히 큽니다.
• 모든 유전자 주파수는 남녀가 같습니다.
• 이동, 유전자 흐름, 혼합물, 돌연변이 또는 선택이 없습니다.

하디-와인버그 가정을 위반하면 예상에서 벗어날 수 있습니다. 이것이 모집단에 어떤 영향을 미치는지는 위반되는 가정에 달려 있습니다.

• 랜덤 짝짓기. HWP는 모집단 내에서 무작위 교배를 한 세대 한 후 모집단이 주어진 유전형 빈도(Hardy-Weinberg proportions라고 함)를 가질 것이라고 말합니다. 랜덤 교배 가정이 위반되면 모집단은 하디-바인버그 비율을 갖지 않습니다. 무작위가 아닌 짝짓기의 흔한 원인은 모든 유전자의 동형접합 증가를 유발하는 근친교배입니다.

모집단이 다음 네 가지 가정 중 하나를 위반할 경우 모집단은 각 세대에서 하디-바인버그 비율을 계속 가질 수 있지만 대립 유전자 빈도는 시간이 지남에 따라 변경됩니다.

• 일반적으로 선택은 모든 대립 유전자 주파수를 매우 빠르게 변화시킵니다. 방향 선택은 결국 선호하는 대립유전자를 제외한 모든 대립유전자의 손실로 이어지지만(이 경우 열성 대립유전자는 낮은 주파수에서 생존할 수 있음), 균형 선택과 같은 일부 형태의 선택은 대립유전자의 손실 없이 평형으로 이어집니다.
• 돌연변이는 집단에 새로운 대립유전자를 도입함으로써 대립유전자 빈도에 매우 미묘한 영향을 미칠 것입니다. 돌연변이율은 10에서⁻⁴ 10⁻⁸ 정도이며 대립유전자 빈도의 변화는 기껏해야 같은 순서일 것입니다. 반복적인 돌연변이는 그들에 대한 강력한 선택이 있더라도 집단 내 대립유전자를 유지할 것입니다.
• 이주는 두 개 이상의 집단을 유전적으로 연결합니다. 일반적으로 대립유전자 주파수는 모집단 사이에서 더 균질해질 것입니다. 마이그레이션에 대한 일부 모델은 본질적으로 비랜덤 교배(예: Wahlund effect)를 포함합니다. 이러한 모형의 경우 일반적으로 하디-와인버그 비율은 유효하지 않습니다.
• 모집단 크기가 작으면 대립유전자 빈도가 무작위로 변경될 수 있습니다. 이것은 샘플링 효과 때문이며, 유전적 드리프트라고 불립니다. 표본 추출 효과는 대립유전자가 적은 수의 사본에 존재할 때 가장 중요합니다.

실제 유전자형 데이터에서 하디-바인베르크 평형으로부터의 편차는 유전자형 오류의 징후일 수 있습니다.^[4][5][6]

성연관

A 유전자가 성에 연결되어 있는 경우, 이종 생식 성별(예: 포유류 수컷, 조류 암컷)은 유전자의 사본이 하나만 있는 반면, 동종 생식 성별(예: 인간 암컷)은 두 개의 사본을 가지고 있습니다. 평형 상태의 유전자형 빈도는 이종 생식 성별의 경우 p와 q이지만 동종 생식 성별의 경우² p, 2pq 및 q입니다².

예를 들어, 인간의 경우 적녹색맹은 X-연관 열성 형질입니다. 서유럽 남성의 경우, 이 특성은 약 12명 중 1명(q = 0.083)에 영향을 미치는 반면, 여성 200명 중 1명(q = 0.007에 비해 0.005)에 영향을 미치며, 이는 하디-바인베르크 비율에 매우 가깝습니다.

각 하위 집단(남성 또는 여성)에서 대립 유전자 빈도가 다른 남녀 집단을 모으면, 각 아들이 어머니로부터 X 염색체를 받기 때문에 다음 세대 남성 집단의 대립 유전자 빈도는 여성 집단의 대립 유전자 빈도를 따라가게 됩니다. 인구는 매우 빠르게 균형에 수렴합니다.

일반화

위의 단순 유도는 2개 이상의 대립유전자 및 배수체에 대해 일반화할 수 있습니다.

두 개 이상의 대립유전자에 대한 일반화

추가 대립유전자 빈도를 생각해 보세요, r. 2-알레르기 경우는 (p + q)의 이항 전개이고,² 따라서 3-알레르기 경우는 (p + q + r)의 삼항 전개입니다.²

${\displaystyle (p+q+r)^{2}=p^{2}+q^{2}+r^{2}+2pq+2pr+2qr\,}$

보다 일반적으로, 대립유전자 빈도₁ p에_1n 의해 주어진 대립유전자 A, ..., A를_n 고려합니다.

${\displaystyle(p_{1}+\cdots +p_{n})^{2}\,}$

모든 동형 접합체에 대해 다음을 제공합니다.

${\displaystyle f(A_{i}A_{i})=p_{i}^{2}\,}$

그리고 모든 이형 접합체에 대해:

${\displaystyle f(A_{i})A_{j})=2p_{i}p_{j}\,}$

배수체에 대한 일반화

하디-바인버그 원리는 배수체 시스템, 즉 각 염색체의 사본이 2개 이상인 유기체에 대해서도 일반화될 수 있습니다. 두 개의 대립유전자만 다시 고려합니다. 이배체 케이스는 다음의 이항 팽창입니다.

${\displaystyle (p+q)^{2}\,}$

따라서 배수체 케이스는 다음의 이항 팽창입니다.

${\displaystyle (p+q)^{c}\,}$

여기서 c는 배수체(c = 4)와 같은 배수체입니다.

표 2: 4배체에 대한 예상 유전자형 빈도

유전자형	빈도수.
아아아.	${\displaystyle p^{4}}$
아아아.	${\displaystyle 4p^{3}q}$
아아아.	${\displaystyle 6p^{2}q^{2}}$
아아아.	${\displaystyle 4pq^{3}}$
아아아.	${\displaystyle q^{4}}$

이 유기체가 '진정한' 4배체인지 아니면 양배체인지는 개체군이 하디-바인베르크 평형에 도달하는 데 얼마나 걸릴지를 결정할 것입니다.

완전 일반화

$c$ ${\displaystyle$ $c$$}-$ploids의 n ${\displaystyle$ n$}$개의 별개의 대립유전자에 대해 하디-바인베르크 평형의 유전자형 빈도는$$(${\displaystyle {p1}_{}{}_{}}$+ ⋯ +$$ n) c ${\displaystyle (p_${1$}+\cdots$+ $p_{$n$\})^\{$c}의 다항식 확장에서 개별 항으로 제공됩니다.

${\displaystyle (p_{1}+\cdots +p_{n})^{c}=\sum _{k_{1},\ldots ,k_{n}\ \in \mathbb {N} :k_{1}+\cdots +k_{n}=c}{c \choose k_{1},\ldots ,k_{n}}p_{1}^{k_{1}}\cdots p_{n}^{k_{n}}}$

편차에 대한 유의성 검정

HWP로부터의 편차 테스트는 일반적으로 데이터에서 얻은 관찰된 유전자형 빈도와 HWP를 사용하여 얻은 예상 유전자형 빈도를 사용하여 Pearson의 카이제곱 테스트를 사용하여 수행됩니다. 많은 수의 대립유전자가 있는 시스템의 경우 가능한 많은 유전자형이 비어 있고 유전자형 수가 적은 데이터가 발생할 수 있습니다. 왜냐하면 샘플에 모든 유전자형 클래스를 적절하게 나타내기에 충분한 개체가 존재하지 않는 경우가 많기 때문입니다. 그렇다면 카이제곱 분포의 점근적 가정은 더 이상 유지되지 않을 것이며, 컴퓨터가 해결해야 하는 피셔의 정확한 검정의 형태를 사용해야 할 수도 있습니다. 최근에는 HWP로부터의 편차에 대한 MCMC 테스트 방법이 많이 제안되었습니다(Guo & Thompson, 1992; Wigginton et al. 2005).

편차에 대한 카이제곱 검정 예제

이 자료는 EB에서 나온 것입니다. 붉은 호랑이 나방에 대한 포드(1971)는 모집단 표본의 표현형을 기록했습니다. 유전자형-표현형 구별은 무시할 수 없을 정도로 작은 것으로 추정됩니다. 귀무 가설은 모집단이 하디-와인버그 비율에 있다는 것이고, 다른 가설은 모집단이 하디-와인버그 비율에 있지 않다는 것입니다.

표 3: 예제 하디-와인버그 원리 계산

표현형	흰점박이(AA)	중급(Aa)	작은 점 (aa)	총
번호	1469	138	5	1612

이를 통해 모든 대립 유전자 주파수를 계산할 수 있습니다.

${\displaystyle {\aligned}p&={2\times \mathrm {obs}({\text{AA})+\mathrm {obs}({\text{Aa}}) \2\time(\mathrm {obs}({\text{AA}})+\mathrm {obs}({\text{Aa}}+\mathrm {obs}({\text{aa}})}\\\\&={2\times 1469+138 \2\times (1469+138+5)}\\\\\&={3076 \over 3224}\\\&=0.954\end{aligned}}$

그리고.

${\displaystyle {begin{aligned}q&=1-p\&=1-0.954\\&=0.046\end{aligned}}$

따라서 하디-와인버그의 예상은 다음과 같습니다.

${\displaystyle {\begin{aligned}\mathrm {Exp}({\text{AA}})&=p^{2}n=0.954^{2}\times 1612=1467.4\\\mathrm {Exp} ({\text{Aa}})&=2pqn=2\times 0.954\times 0.046\times 1612=141.2\\\mathrm {Exp} ({\text{aa}})&=q^{2}n=0.046^{2}\times 1612=3.4\end{align}}}$

Pearson의 카이제곱 검정은 다음과 같습니다.

${\displaystyle {\begin{aligned}\chi ^{2}&=\sum {(O-E)^{2} \over E}\\&={(1469-1467.4)^{2} \over 1467.4}+{(138-141.2)^{2} \over 141.2}+{(5-3.4)^{2} \over 3.4}\\&=0.001+0.073+0.756\\&=0.83\end{aligned}}}$

자유도는 1입니다(하디-와인버그 비율에 대한 검정의 자유도는 #유전자형 - # 대립유전자). 자유도 1에 대한 5% 유의 수준은 3.84이며, χ 값이 이보다 작으므로 모집단이 하디-바인베르크 주파수에 있다는 귀무 가설은 기각되지 않습니다.

Fisher의 정확한 검정(확률 검정)

Fisher의 정확한 검정은 Hardy-Weinberg 비율에 대한 검정에 적용될 수 있습니다. 검사는 대립유전자 빈도인 p와 q를 조건으로 하므로 문제는 적절한 이형접합체 수에 대한 검사로 볼 수 있습니다. 이러한 방법으로 이형접합체의 수가 너무 많거나 적으면 하디-와인버그 비율의 가설은 기각됩니다. Emmigh(1980)에서 대립유전자 빈도가 주어진 이형접합체에 대한 조건부 확률은 다음과 같습니다.

${\displaystyle \operatorname {prob} [n_{12}\mid n_{1}]={\frac {\binom {n}{n_{11},n_{12},n_{22}}}{\binom {2n}{n_{1},n_{2}}}}2^{n_{12}},}$

여기서 n, n, n은 각각 AA, Aa 및 Aa의 세 가지 유전자형의 관찰된 수이고, n은 A 대립유전자의 수이며, 여기서 ${\displaystyle n_{}}$ 1 = ${\displaystyle 2}$ n ${\displaystyle {11}_{}}$+$$n 12 {\display n_{1} = 2 n_{11}+ n_{12}}입니다.

예제 Emigh(1980)의 예제 중 하나를 사용하여 n = 100이고 p = 0.34인 경우를 고려할 수 있습니다. 관찰 가능한 이형 접합체 및 정확한 유의 수준은 표 4에 나와 있습니다.

표 4: N = 100, p = 0.34에 대한 Fisher의 정확한 검정 예제.

이형접합체의 수	유의수준
0	0.000
2	0.000
4	0.000
6	0.000
8	0.000
10	0.000
12	0.000
14	0.000
16	0.000
18	0.001
20	0.007
22	0.034
34	0.067
24	0.151
32	0.291
26	0.474
30	0.730
28	1.000

이 표를 사용하면 관찰된 이형 접합체 수를 기준으로 검정의 유의 수준을 확인할 수 있습니다. 예를 들어, 20개의 이형 접합체를 관찰한 경우 검정의 유의 수준은 0.007입니다. 작은 표본에 대한 Fisher의 정확한 검정에서 일반적인 것처럼 유의 수준의 그라데이션은 매우 조잡합니다.

그러나 표는 n과 p에 모두 의존하기 때문에 모든 실험에서 이와 같은 표를 만들어야 합니다.

동등성 검정

동등성 테스트는 관찰된 유전자형 빈도와 하디 와인버그 평형의 충분히 좋은 일치를 확립하기 위해 개발됩니다. $M{\displaystyle \mathcal{}}$ ${\$이(가) 하디 와인버그 평형 가정 하에서 유전자형 분포의 계열을 나타낸다고$$ 가정합니다. 유전자형 분포 $p$ ${\displaystyle$ p$}$와 하디 와인버그 평형 사이의 거리는 $d{\displaystyle (p,}$ M${\displaystyle )}$ = ${\displaystyle \underset{}{min}}$ ${\displaystyle q}$ ∈${\displaystyle }$Md$($$p$, q) {\$displaystyle$ d(p, {\mathcal {M}} =\min _{q\in {\mathcal {M}} d(p,q)}로 정의되며, 여기서 d {\displaystyle d}는 어느 정도의 거리입니다. The equivalence test problem is given by ${\displaystyle H_{0}=\{d(p,{\mathcal {M}})\geq \varepsilon \}}$ and ${\displaystyle H_{1}=\{d(p,{\mathcal {M}})<\varepsilon \}}$, where ${\displaystyle \varepsilon >0}$ is a tolerance parameter. 가설 $H{\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\$이 기각될$$ 수 있는 경우 모집단은 높은 확률로 하디 와인버그 평형에 가깝습니다. Biallelic 사례에 대한 동등성 테스트는 Welllek(2004)의 다른 것들 중에서 개발되었습니다.^[8] Ostrovski(2020)에서는 다중 대립유전자의 경우에 대한 동등성 테스트를 제안합니다.^[9]

근친교배계수

근친교배 계수인 $F{\displaystyle }$ ${\displaystyle F}($F-통계 참조)는 하디-바인베르크 평형에서 예상되는 것보다 관찰된 이형접합체의 빈도를 뺀 값입니다.

${\displaystyle F={\frac {\operatorname {E} {(f({\text{Aa}})}-\operatorname {O}(f({\text{Aa}})}{\operatorname {E}(f({\text{Aa})}}}=1-{\frac {\operatorname{O}(f({\text{Aa}))}{\operatorname {E} (f({\text{Aa}}))}},}$

여기서 하디-바인베르크 평형으로부터 기대되는 값은 다음에 의해 주어집니다.

${\displaystyle \operatorname {E}(f({\text{Aa}})=2pq}$

예를 들어, 위의 포드 데이터의 경우:

${\displaystyle F=1-{138 \over 141.2}=0.023.}$

두 대립유전자의 경우 하디-와인버그 비율에 대한 카이-squared 적합도 검정은 근친 교배 ${\displaystyle \mathrm{검정}}$인 F = 0$${\$displaystyle F$ = 0$\}$과 같습니다.

근친교배 계수는 기대값이 0에 가까워짐에 따라 불안정하므로 희귀하고 매우 일반적인 대립유전자에는 유용하지 않습니다. ${\displaystyle {}_{}}$ = $,$ O = 0 = - ∞ {\displaystyle F{\big}_{E = 0, O = 0} = -\infty}의 경우 FE = 0, O > 0 {\displaystyle F{\big}_{E = 0, O > 0}이(가) 정의되지 않았습니다.

역사

멘델의 유전학은 1900년에 재발견되었습니다. 그러나 어떻게 지속적인 특성을 유발할 수 있는지 그때는 알려지지 않았기 때문에 몇 년 동안 다소 논란의 여지가 있었습니다. 우디 율레(Udny Yule, 1902)는 지배적인 대립유전자가 개체수에서 증가할 것이라고 생각했기 때문에 멘델주의에 반대했습니다.^[10] 미국인 윌리엄 E. Castle(1903)은 선택이 없으면 유전자형 빈도가 안정적으로 유지됨을 보여주었습니다.^[11] 칼 피어슨(1903)은 p = q = 0.5의 값을 갖는 하나의 평형 위치를 찾았습니다. 율레의 지적을 반박할 수 없었던 레지널드 퍼넷(Reginald Punnett)은 영국 수학자 G. H. 하디(G. Hardy)에게 문제를 소개했고, 그는 크리켓 경기를 함께 했습니다. 하디는 순수한 수학자였고 응용수학을 경멸했습니다. 생물학자들의 수학 사용에 대한 그의 관점은 1908년 논문에서 발견되었는데, 그는 이것을 "매우 단순하다"고 설명했습니다.^[13]

과학 편집자에게: 저는 전문 지식이 없는 문제에 대한 토론에 끼어들기를 꺼리고, 생물학자들에게 친숙하기를 바라는 아주 간단한 점을 예상했어야 합니다. 하지만, R. C. Punnett씨가 제 주의를 환기시킨 Udny Yule씨의 몇몇 발언은, 그것이 여전히 가치가 있을지도 모른다는 것을 암시합니다.

Aa가 멘델 문자의 쌍이고, A가 우세하며, 어떤 세대에서 순수한 지배자(AA), 이형접합체(Aa) 및 순수 열성(Aa)의 수가 p:2q:r이라고 가정합니다. 마지막으로, 짝짓기를 무작위로 간주할 수 있도록 그 수가 상당히 많고, 성별이 세 가지 품종 사이에 고르게 분포되어 있으며, 모든 것이 똑같이 비옥하다고 가정합니다. 곱셈표 유형에 대한 약간의 수학은 다음 세대에서 숫자가 (p + q):²2(p + q)(q + r):(q + r),² 또는₁ p:2q₁:r₁, 예를 들어 다음과 같이 될 것이라는 것을 보여주기에 충분합니다.

흥미로운 질문은 이 분포가 어떤 상황에서 이전 세대의 분포와 같을까 하는 것입니다. 이에 대한 조건이 q = pr임을 쉽게 알 수 있습니다. 그리고 q = pr이기 때문에 p, q, r 값이 무엇이든 간에 분포는 2세대 이후에도 변하지 않고 계속됩니다.

따라서 이 원리는 1943년 커트 스턴이 독일 의사 빌헬름 와인버그에 의해 최초로 독립적으로 공식화되었다고 지적할 때까지 영어권에서 하디의 법칙으로 알려졌습니다.^[14][15] 1903년 윌리엄 성은 대립유전자 빈도가 동일한 특수한 경우에 대한 비율을 도출하기도 했으며, 때때로 (거의) 하디-바인베르크-성 법칙이라고 불립니다.

하디 방정식의 유도

하디의 진술은 주파수 p, 2q, r에 대한 반복 관계로 시작됩니다. 이러한 재발 관계는 확률, 구체적으로 독립성 및 조건부 확률의 기본 개념을 따릅니다. 예를 들어, ${\$ t$}$ 세대의 자손이 동형접합 $우성일$ 확률을 생각해 보십시오. 대립 유전자는 각 부모로부터 독립적으로 상속됩니다. 우성 대립유전자는 확률이 1인 동형 접합 우성 부모로부터 또는 확률이 0.5인 이형 접합 부모로부터 유전될 수 있습니다. 이 추론을 수식으로 나타내기 위해 ${\displaystyle {At}_{}}$ ${\$가 상위 대립유전자의 상속을 나타낸다고$$ 합니다. 또한 ${\displaystyle {Aat}_{}}$- ${\displaystyle 1_{}}$ ${\$ 및$$ ${\displaystyle {Aat}_{}}$- ${\displaystyle 1_{}}$ ${\$\textstyle $Aa_{t-1}}$은 이전 세대의 잠재적인 부모 유전자형을 나타냅니다$$.

${\displaystyle {\begin{aligned}p_{t}&=P(A_{t},A_{t})=P(A_{t})^{2}\\&=\left(P(A_{t}\mid AA_{t-1})P(AA_{t-1})+P(A_{t}\mid Aa_{t-1})P(Aa_{t-1})\right)^{2}\\&=\left((1)p_{t-1}+(0.5)2q_{t-1}\right)^{2}\\&=\left(p_{t-1}+q_{t-1}\right)^{2}\end{aligned}}}$

다른 유전자형에 적용된 동일한 추론은 나머지 두 개의 재발 관계를 산출합니다. 균형은 각 비율이 후속 세대 사이에서 일정할 때 발생합니다. 좀 더 공식적으로, $모집단$은$${\$displaystyle \textstyle$t} 생성 시 평형 상태에 있습니다.

${\displaystyle \mathrm{}0}$ = p$$${\displaystyle }$- $p$ $t$- 1 ${\displaystyle \textsty$${\displaystyle \mathrm{l}}$$e$ 0 = p_{$t}-$p_${t-1}$${\displaystyle \mathrm{\}}}$$,$ 0 = q t - q t - 1 {\displaystyle \textsty${\displaystyle \mathrm{l}}$e 0 = q_{t}-q_{t-1}${\displaystyle \mathrm{\}}}$, 0 = r t - r t - 1 {\displaystyle \textsty${\displaystyle \mathrm{l}}$e 0 = r_{t}-r_{t-1}}

이 방정식들을 풀면 평형이 일어나기 위한 필요조건과 충분한 조건을 결정할 수 있습니다. 다시, 동형접합 우성 동물의 빈도를 고려합니다. 평형은 다음을 의미합니다.

${\displaystyle {\begin{aligned}0&=p_{t}-p_{t-1}\\&=p_{t-1}^{2}+2p_{t-1}q_{t-1}+q_{t-1}^{2}-p_{t-1}\end{aligned}}}$

$먼저$ p ${\displaystyle {\mathrm{t}}_{}}$- 1 = ${\$displaystyle$\textstyle$ p_${t-1$}=$0}$인 대소문자를 고려하고 q t - 1 = 0 {\displaystyle \textstyle q_{t-1}= 0} 및 r t - 1 {\displaystyle \textstyle r_{t-1}= 1}인 경우를 고려합니다. 이제 나머지 대소문자를 고려합니다. 여기서 ${\displaystyle p_{}}$- $1$≠ 0 ${\displaystyle$ \$textstyle p_${t-1}\n$eq \textstyle$ 0$\}:$

${\displaystyle {\begin{aligned}0&=p_{t-1}(p_{t-1}+2q_{t-1}+q_{t-1}^{2}/p_{t-1}-1)\\&=q_{t-1}^{2}/p_{t-1}-r_{t-1}\end{aligned}}}$

대립유전자 비율이 1을 합산해야 하기 때문에 최종적으로 동일성이 유지되는 경우. 두 경우 모두 $q$ ${\displaystyle t_{}^{}}$- ${\displaystyle {}_{}^{}}$ = ${\displaystyle p_{}}$ t$$- 1 r t - 1 {\displaystyle \textstyle q_{t-1}^{2} = p_{t-1}r_{t-1}}입니다. 다른 두 평형 조건이 동일한 방정식을 내포한다는 것을 알 수 있습니다. 세 가지 평형 방정식의 해는 평형에 대한 하디 조건의 충분성을 의미합니다. 그 조건이 항상 2세대에게 적용되기 때문에, 모든 후속 세대는 동일한 비율을 가지고 있습니다.

수치 예제

유전자형 분포 추정

하디의 원래 방정식에 의해 주어진 유전자형 분포의 예시적인 계산은 유용합니다. 상기 표 3의 표현형 분포는 하디의 초기 유전자형 분포를 계산하는 데 사용될 것입니다. 하디가 사용한 p와 q 값은 위에서 사용한 값과 같지 않습니다.

${\displaystyle {\begin{aligned}{\text{sum}}&={\mathrm {obs}({\text{AA})+2\times \mathrm {obs}({\text{Aa}}+\mathrm {obs}({\text{aa}}}={1469+2\times 138+5}\[5pt]&=1750\end{aligned}}$

${\displaystyle {begin{aligned}p&={1469 \over 1750}= 0.83943\\[5pt]2q&={2\times 138 \over 1750}=0.15771\[5pt]r&={5 \over 1750}=0.00286\end{aligned}}}$

분포를 확인할 때 계산

${\displaystyle p+2q+r=0.83943+0.15771+0.00286=1.00000\,}$

그리고.

${\displaystyle E_{0}=q^{2}-pr=0.00382.\,}$

다음 세대를 위해 하디의 방정식은

${\displaystyle {\begin{aligned}q&={0.15771 \over 2}=0.07886\\\\p_{1}&=(p+q)^{2}=0.84325\\[5pt]2q_{1}&=2(p+q)(q+r)=0.15007\\[5pt]r_{1}&=(q+r)^{2}=0.00668.\end{align}}}$

분포에 대한 검사로 다시 계산합니다.

${\displaystyle p_{1}+2q_{1}+r_{1}=0.84325+0.15007+0.00668=1.00000\,}$

그리고.

${\displaystyle E_{1}=q_{1}^{2}-p_{1}r_{1}=0.00000\,}$

이 값은 기대 값입니다. 독자는 3세대에 대해 2세대 값을 후속적으로 사용하면 동일한 결과를 얻을 수 있음을 입증할 수 있습니다.

반송파 주파수 추정

하디-와인버그 원리는 또한 고통의 빈도를 기반으로 집단에서 상염색체 열성 상태의 보균자의 빈도를 추정하는 데 사용될 수 있습니다.

$추정{\displaystyle \frac{\mathrm{}}{}}$ 1,${\displaystyle \frac{2500}{}}$ ${\$명의$$ 아기가 낭포성 섬유증을 가지고 태어난다고 가정해 보겠습니다. 이는 북유럽 인구에서 관찰되는 동형접합 개체의 빈도에 대한 것입니다. 우리는 하디-와인버그 방정식을 사용하여 반송파 주파수, 이형접합 개체의 주파수, ${\displaystyle \mathrm{2p}}$ ${\displaystyle q}${\$displaystyle$ \$textstyle 2pq}$를 추정할 수 있습니다$.$

${\displaystyle {\begin{aligned}&q^{2}={\frac {1}{2500}}\\[5pt]&q={\frac {1}{50}\[5pt]&p=1-q\end{aligned}}$

${\displaystyle \frac{150}{}}$ ${\$이(가) 작으므로 p${\displaystyle ,}$ $- 150$ {\displaystyle \$textstyle 1-{\frac {1$$50}}$을 1로 할 수 있습니다.

${\displaystyle {\begin{aligned}2pq=2\cdot {\frac {1}{50}}\\[5pt]2pq={\frac {1}{25}}\end{aligned}}}$

따라서 저희는 반송파 $속도$를 북유럽 인구에서 관찰되는 빈도와$$${\displaystyle \frac{\mathrm{유사}}{}}$한$$125 {\$displaystyle$ \$textstyle${\$frac${1}{25$}}$로 추정합니다.

이는 반송 주파수가 출생 주파수의 제곱근의 약 2배인 것으로 단순화될 수 있습니다.

그래픽 표현

de Finetti 다이어그램을 사용하여 모집단 내의 bi-allic locus에 대한 유전자형 빈도 분포를 그래픽으로 나타낼 수 있습니다. 이것은 삼각형 그림(삼선형, 삼축 또는 삼원형 그림이라고도 함)을 사용하여 서로에 대한 세 유전자형 빈도의 분포를 나타냅니다. 축 중 하나의 방향이 반대로 바뀐다는 점에서 다른 많은 그림과 다릅니다.^[16] 다이어그램에서 곡선은 하디-바인베르크 포물선이며 대립유전자가 하디-바인베르크 평형에 있는 상태를 나타냅니다. 자연 선택의 효과와 대립유전자 빈도에 미치는 영향을 이러한 그래프에 나타낼 수 있습니다.^[17] 드 피네티 다이어그램은 A가 개발하고 광범위하게 사용했습니다. W.F. 에드워즈는 ^[18]그의 책 수학적 유전학의 기초에서

참고 항목

• 평균에 대한 회귀
• 다항 분포(Hardy–Weinberg는${\displaystyle {}^{}}$확률$($θ 2, 2${\displaystyle {}^{}}$θ${\displaystyle (1}$ - θ${\displaystyle )),}$ (1 -$$θ$) 2)$ {\$displaystyle(\theta$ ^{2$},$ 2\$theta$(1-$\backslash$theta), (1-\theta )^{2}}
• 가산 불균형 및 z 통계량
• 집단유전학
• 유전적 다양성
• 창시자효과
• 인구병목
• 유전자 드리프트
• 근친 우울증
• 자연선택
• 피트니스
• 유전자 부하

메모들

참고문헌

인용

원천

외부 링크

• Evolution 솔루션(페이지 하단)
• 하디-바인베르크 평형계산기
• 유전자 집단 유전학 시뮬레이터^{[영구적 데드링크]}
• 1992년 궈앤톰슨의 HARDI C 시행
• Wigginton et al. 2005의 소스 코드(C/C++/Fortran/R)
• Online de Finetti Diagram Generator와 Hardy-Weinberg 평형 검정
• 2015년 5월 26일 Wayback Machine에서 온라인 하디-와인버그 평형 테스트 및 de Finetti 다이어그램 그리기
• 하디-바인베르크 평형계산기