힐버트의 여덟 번째 문제

힐버트의 여덟 번째 문제는 1900년에 제기된 데이비드 힐버트의 열린 수학 문제 목록 중 하나이다.그것은 숫자 이론, 특히 리만 가설과 관련이 있지만 골드바흐 추측과도 관련이 있다.^[1]언급된 문제는 프라임을 대신하는 다른 고리에 프라임과 리만 가설을 일반화하는 것에 대한 더 많은 작업을 요구하였다.

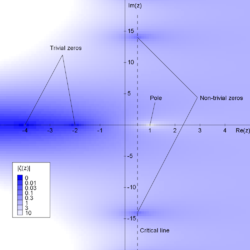
ζ 함수의 절대값.힐버트의 여덟 번째 문제에는 리만 가설이 포함되어 있는데, 이 가설은 이 함수가 x = 1/2 선에 비종교적 영점만을 가질 수 있다는 것을 명시하고 있다.

하위 주제

힐버트는 리만 가설에 대한 해결책을 요구하는데, 이 가설은 오랫동안 수학에서 가장 깊이 열려 있는 문제로 여겨져 왔다.해법으로 볼 때 리만의 제타 기능과 프라임 넘버 정리에 대해 좀 더 철저한 조사를 요구하는 것이다.^[2]

그는 고정된 선형 디오판틴 방정식을 풀어나가는 무한히 많은 쌍의 프라임들을 찾아내는 것과 같은 더 일반적인 문제들뿐만 아니라 골드바흐 추측에 대한 해결책을 요구한다.

마지막으로, 그는 수학자들이 리만 가설에 대한 사상을 숫자 분야에서 주요한 이상을 세는 것으로 일반화할 것을 요구한다.

Bombieri, Enrico (2006), "The Riemann Hypothesis", The millennium prize problems, Clay Mathematics Institute Cambridge, MA: 107--124
Moxley, Frederick (2021), "Complete solutions of inverse quantum orthogonal equivalence classes", Examples and Counterexamples, 1: 100003