힐버트의 네 번째 문제
Hilbert's fourth problem수학에서 1900년 힐버트의 문제 목록에서 힐버트의 네 번째 문제는 기하학에서 기초적인 질문이다.원문에서 도출된 한 진술에서, 그것은 이소모르피즘까지, 고전 기하학(유클리드, 쌍곡선, 타원형)의 자명적 체계를 가진 모든 기하학적 구조를 찾는 것이었으며, 각도의 개념을 포함하는 일치성의 공리와 공리로 간주되는 '삼각 불평등'이 추가되었다.
만약 어떤 사람이 연속성 공리를 추가로 가정한다면, 유클리드 비행기의 경우, 우리는 장 가스통 다부스가 제기하는 문제에 도달한다: "해법이 모두 평면 직선인 평면의 모든 변동 문제의 미적분을 결정하기 위해서"[1]
데이비드 힐버트의 원문에 대해서는 몇 가지 해석이 있다.그럼에도 불구하고, 독일 수학자 게오르크 하멜이 힐베르트의 네 번째 문제 해결에 가장 먼저 기여하는 것으로 해법이 모색되었다.[2]
인정된 해결책은 1973년 우크라이나 수학자 알렉세이 포고로프(Aleksie Pogorelov)에 의해 제시되었다.[3][4]1976년 아르메니아의 수학자 루벤 5세. Ambartzumian은 힐버트의 네 번째 문제에 대한 또 다른 증거를 제시했다.[5]
원문
힐버트는 비유클리드 기하학과 비아키메데스 기하학의 존재를 논한다.
...일반적인 유클리드 기하학의 모든 공리, 특히 삼각형의 합치 중 하나를 제외한 모든 합치 공리(또는 이소체 삼각형의 염기 각도의 동일성의 정리를 제외한 모든 것)와, 게다가 모든 삼각형에서 양면의 합이 더 크다는 명제가 들어 있는 기하학.한 세 번째 공리는 특정한 공리로 가정된다.[6]
'직선'이 두 점 사이의 최단 경로로 정의된다는 생각 때문에, 그는 평면상의 직선이 두 점 사이의 최단 거리라는 유클리드(유클리드)의 입증에 삼각형의 합치가 어떻게 필요한지를 언급한다.그는 다음과 같이 요약한다.
두 점 사이의 최단거리로서의 직선의 정리와 삼각형의 측면에 대한 유클리드(유클리드)의 본질적으로 동등한 정리는 숫자 이론뿐만 아니라 표면 이론과 변동의 미적분학에서도 중요한 부분을 담당한다.이 때문에, 그리고 이 정리의 타당성을 위한 조건의 철저한 조사가 거리라는 개념뿐만 아니라, 다른 기초적인 관념, 예를 들어 비행기의 관념에 대해서도, 직선, 건설, 그리고 그 정의의 가능성에 대해서도 새로운 빛을 던질 것이라고 믿기 때문이다.여기서 가능한 기하학적 구조의 체계적 처리가 내게는 바람직해 보인다.[6]
플랫 메트릭
삼각형의 해당 정점을 연결하는 선들이 한 점에서 만나는 평면에 두 개의 삼각형이 놓여 있다면, 삼각형의 해당 면의 세 쌍의 연장선이 교차하는 세 개의 점이 한 선에 놓여 있다.
힐버트의 네 번째 문제를 해결하는 데 필요한 조건은 이 문제의 공리를 만족시키는 미터법 공간은 데스투게시안이 되어야 한다는 요건이다.
- 공간이 차원 2인 경우, 데스아게스의 정리와 그 역은 유지되어야 한다.
- 공간이 2보다 크면 세 개의 점이 한 평면에 놓여 있어야 한다.
데스카게스 공간에 대해 게오르크 하멜은 힐버트의 네 번째 문제의 모든 해결책이 실제 투영 공간 R 또는 특수 측정 기준에서 길이의 동일성에 의해 세그먼트의 합치를 결정하는 경우 P 의 볼록 영역으로 표현될 수 있음을 증명했다.투사 공간의 선은 지질학이다.
이러한 유형의 측정 기준을 플랫 또는 투영이라고 한다.
따라서 힐버트의 네 번째 문제 해결은 모든 완전한 평편한 측정기준의 건설적인 결정의 문제 해결로 축소되었다.
하멜은 미터법의 높은 규칙성을 가정하여 이 문제를 해결했다.[2]그러나 단순한 예에서 알 수 있듯이, 일반 플랫 메트릭의 클래스는 모든 플랫 메트릭의 클래스보다 작다.고려 중인 기하학의 공리는 지표의 연속성만을 의미한다.따라서 힐버트의 네 번째 문제를 완전히 해결하기 위해서는 모든 연속적인 플랫 메트릭스를 건설적으로 결정할 필요가 있다.
힐베르트의 네 번째 문제의 선사시대
1900년 이전에는 단위 디스크에서 로바체프스키 기하학의 케이리-클레인 모델이 알려져 있었는데, 이에 따라 지오데틱 선은 디스크의 화음이고 지점 사이의 거리는 4중 교차 비율의 로그로 정의된다.2차원 리만 지표에 대해, Eugenio Beltrami(1835–1900)는 플랫 지표가 일정한 곡률의 지표라는 것을 증명했다.[7]
다차원 리만 지표에 대해 이 진술은 1930년 E. Cartan에 의해 증명되었다.
1890년, 숫자 이론의 문제를 해결하기 위해 헤르만 민코프스키가 오늘날 유한차원 바나흐 공간이라고 불리는 공간의 개념을 도입했다.[8]
민코스키 공간
F 은(는) 에 의해 정의된 유클리드 공간에서 콤팩트 볼록한 하이퍼러페이스가 되도록 한다.
여기서 = F( ) 함수가 다음 조건을 만족한다.
- 그리고 F y i j> 의 형식은 확실히 정해져 있다.
벡터 OA의 길이는 다음과 같이 정의된다.
이 지표가 있는 공간을 민코스키 공간이라고 한다.
하이퍼페이스 은 볼록하며 불규칙할 수 있다.정의된 메트릭은 평탄하다.
지느러미 공간
= {( x, ) x ,y x xM\}}}}은(는) 각각 매끄러운 유한차원 다지관과 접선다발이다., y): T →[ 0,+ ) 은 다음과 같은 경우 핀슬러 메트릭이라고 한다.
- ( , y) k { ),
- 임의의 지점 x M에 대해 M 에 F ){\의 제한은 민코스키 표준이다.
, ) (M은 핀슬러 공간이다.
힐베르트의 기하학
(+ , . ) U을(를) 등급 C의2 경계와 양의 정규 곡선으로 경계된 개방 볼록 집합으로 두십시오.로바체프스키 공간과 유사하게 하이퍼페이스 는 힐베르트의 기하학의 절대적이라 불린다.[9]
힐버트의 거리(그림 참조)는 다음과 같이 정의된다.
d U 은(는) 에 Hilbert-Finsler 메트릭 및 y x 을(를) 유도한다.
미터법은 대칭적이고 평평하다.1895년 힐버트는 로바체프스키 기하학의 일반화로서 이 지표를 도입하였다.하이퍼페이스 이(가) 타원체라면 Lobachevsky 지오메트리가 있다.
펑크 미터법
1930년에 펑크는 비대칭 측정법을 도입했다.닫힌 볼록초면에 의해 경계된 영역으로 정의되며 또한 평평하다.
σ-metrics
플랫 메트릭스를 위한 충분한 조건
게오르크 하멜은 힐버트의 네 번째 문제 해결에 처음으로 기여했다.[2]그는 다음과 같은 진술을 증명했다.
정리.일반 핀들러 F,) = , ,x , , , …,) 다음 조건을 만족하는 경우에만 평탄하다.
크로프톤식
평면의 모든 방향 선 세트를 고려하십시오.각 선은 {\} {, {\에 의해 정의되며 여기서 은 원점에서 선까지의 거리, }은 선과 x 축 사이의 각도이다.그러면 모든 방향 선 세트가 면적 = d φ { \d=d을(를) 가진 반지름 1의 원형 실린더에 대해 동형이다. 은(는) 평면에서 수리가 가능한 곡선이다.그러면 의 길이는
여기서 은(는) 을를 교차하는 선들의 집합이며 n (, )}은 {\displaystyle\을(으)[10]로 한 선의 교차로 수입니다 크로프톤은 1870년에 이 진술을 증명했다.
유사한 진술이 투영적인 공간을 차지한다.
블래쉬케-부세만 측도
1966년 모스크바에서 열린 국제수학회의 강연에서 허버트 부세만은 새로운 종류의 평판 지표를 도입했다.투사 평면 개의 선 세트에서 그는 다음 조건을 만족하는 완전히 첨가된 비음극 측정 을를) 소개했다.
- ( P)= 여기서 P 은 P 지점을 통과하는 직선의 집합이다.
- ( )> 여기서 는 직선 세그먼트를 포함하는 어떤 집합 X를 통과하는 직선의 집합이다.
- ( ) 은(는) 유한하다.
If we consider a -metric in an arbitrary convex domain of a projective space , then condition 3) should be replaced by the following: for any set H such that H is contained in and the closure of H does not i 의 경계 불평등
- ( )< H hold.[11]
이 측정을 사용하여 R 의 -metric on P 2 에 의해 정의된다.
여기서 [ x, 은(는) 세그먼트 [ , y ] 을(를) 교차하는 직선의 집합이다
이 측정기준에 대한 삼각불평등은 파슈의 정리로부터 따온 것이다.
정리. 2 평평하다. 즉, 지오데틱은 투사 공간의 직선이다.
그러나 Busemann은 메트릭스가 모든 평탄한 메트릭스를 소진한다는 생각과는 거리가 멀었다.그는 "지오디컬이 주어진 지오디컬을 가진 지표를 선택하는 자유는 비 리만 지표가 너무 커서 모든 데스카게스적 공간에 대한 설득력 있는 특성화가 실제로 존재하는지 의심받을 수 있다"고 썼다.[11]
2차원 케이스
포고렐로프의 정리
다음의 훌륭한 정리는 1973년[3][4] 포고렐로프에 의해 증명되었다.
정리.모든 2차원 연속 전체 평면 메트릭은 -metric이다.
이리하여 힐버트의 4번째 2차원 사건 문제는 완전히 해결되었다.
그 결과 동일한 평면형 볼록형 모양의 두 복사본에 경계를 접착할 수 있으며, 그 사이에 각도가 꼬이면 주름선이 없는 3D 물체를 얻을 수 있으며, 두 얼굴을 현상할 수 있다.
암바츠미안의 교정쇄
1976년 암바르트수미안은 힐버트의 네 번째 문제에 대한 또 다른 증거를 제시했다.[5]
그의 증거는 2차원 사례에서 전체 측도는 비앙글에 대한 값에 의해 복원될 수 있고, 따라서 삼각형의 영역이 구체에 정의되는 것과 같은 방식으로 삼각형에 정의될 수 있다는 사실을 이용한다.삼각형 불평등이 유지되기 때문에, 이 측정치는 비감속 삼각형에서 양성이며 모든 보렐 집합에서 결정된다.그러나 이 구조는 힐버트의 세 번째 문제 때문에 더 높은 차원으로 일반화할 수 없다.
2차원 사례에서 같은 부피의 폴리곤은 가위 겸용이다.Dehn에 의해 보여진 것처럼 이것은 더 높은 차원에 대한 사실이 아니다.
입체 케이스
3차원 사례에 대해 포고렐로프는 다음과 같은 정리를 증명했다.
정리. 모든 3차원 정규 완전 평면 메트릭은 -metric이다.
그러나 3차원 사례 - 측정은 양수 또는 음수 값을 취할 수 있다.집합 의 함수로 정의한 일반 메트릭이 평탄해지도록 하기 위해 필요한 조건과 충분한 조건은 다음과 같은 세 가지 조건이다.
- 모든 평면에서 값 \ \은(는) 0이며,
- 모든 원뿔의 값 }은(는) 음수가 아니며,
- 콘에 내부 포인트가 포함되어 있으면 값 \ \}이가) 양수임.
더욱이 포고렐로프는 3차원 사례에서 완전한 연속 평면 메트릭은 메트릭스 도메인의 모든 소형 하위 도메인에서 균일한 수렴을 갖는 정규 metrics의 한계임을 보여주었다.그는 그것들을 일반화된 \sigma - 미터법이라고 불렀다.
이리하여 포고렐로프는 다음과 같은 진술을 증명할 수 있었다.
정리. 3차원 사례에서 완전한 연속 평면 메트릭은 일반화된 의미의 메트릭이다.
부세만은 포고렐로프의 저서 '힐버트의 네 번째 문제'에 대한 평론에서 "힐버트가 자신을 n = 2, 3으로 제한했던 시대정신 속에서 포고렐로프도 그렇게 한다.하지만, 이것은 의심할 여지 없이 교육학적인 이유가 있는데, 그는 폭넓은 독자들을 다루고 있기 때문이다.실제 차이는 n = 2와 n >2이다.포고렐로프의 방법은 n>3에 효과가 있지만 더 큰 기술력을 필요로 한다."[12]
다차원 케이스
제4 힐베르트 문제의 다차원적인 경우는 스자보가 연구했다.[13]1986년 그는 글을 쓰면서 포고렐로프 일반화 정리를 증명했다.
정리.클래스 + , > 의 각 n차원 데카게스 공간은 Blaschke-Buzeman 시공에 의해 생성된다.
측정값을 생성하는▼ {\ -측정에는 다음과 같은 속성이 있다.
- 고정 지점을 통과하는 하이퍼플레인의 - -은 0과 같다.
- 두 세그먼트[x, y, [y, z]를 교차하는 하이퍼플레인 세트의 -measure은 양의 값이다. 여기서 x, y, тissa z는 colinar가 아니다.
Blaschke-Busemann 건설에 의해 생성되지 않은 평평한 미터법의 예가 주어졌다.Szabo는 일반화된 함수의 관점에서 모든 연속적인 플랫 메트릭스를 설명했다.
힐버트의 네 번째 문제와 볼록한 몸
힐버트의 네 번째 문제는 볼록한 신체의 성질과도 밀접한 관련이 있다.볼록한 다면체는 민코프스키의 세그먼트 합이라면 조노토프라고 불린다.블래쉬케-하우스도르프 미터법에서 조노토프의 한계인 볼록한 몸을 조노이드라고 부른다.조노이드의 경우 서포트 함수는
여기서 ( 는 S- - 에 대한 짝수 양의 보렐 측정값이다
민코스키 공간은 인디케이터릭스의 지원 기능이 (1)의 형태를 갖는 경우에만 블래쉬케-부세만 건설에 의해 생성되며, 여기서 스타일 는 반드시 포지티브 보렐 측정치가 아니며, 반드시 그렇지는 않다.[14]그러한 초자극에 의해 둘러싸인 몸을 일반화된 조노이드라고 부른다.
유클리드 + + 1\leqslant 은는) 일반화된 조노이드()가 아니다.위의 문장에서 표준 x = { x , , \1}, x_{\}}}}}}을(를) 가진 민코스키 공간의 평탄한 메트릭은 Blaschke-Busemann 건설에 의해 생성되지 않는다는 것을 따른다.
힐버트의 네 번째 문제 일반화
Planar n-차원 핀슬러 측정 기준과 Grassmann G(+ ,2) в + n+1}에서 관련성이 발견되었다[15]
힐버트의 네 번째 문제에는 주기적인 해결책이 고려되었다.
1) (M, g) 지역 유클리드 리만 다지관이 되게 한다. g에서와 동일한 지오데틱을 가진 M에 C 2 핀슬러 메트릭이 주어진다고 가정합시다.그 다음 핀슬러 메트릭은 로컬 민코프스키 메트릭과 닫힌 1-폼의 합이다.[16]
2) (M, g) 1위 이상의 콤팩트한 대칭 리만 공간이 되게 한다.F가 리만 메트릭 g의 지오디컬과 일치하는 지오디컬 핀슬러 메트릭인 경우, (M, g)는 대칭 핀슬러 공간이다.[16]상위 1위 대칭 공간에 대한 이 정리의 유사성은 아직 입증되지 않았다.
힐베트르트의 네 번째 문제에 대한 또 다른 설명은 파이바의 작품에서 찾을 수 있다.[17]
미해결 문제
- 비대칭 핀슬러 지표에 대한 힐버트의 네 번째 문제는 아직 해결되지 않았다.
- k-plane이 k-area를 최소화하는 에 대한 메트릭 설명(Busemann)[18]
참조
- ^ G. Darboux, Lecons sur ra theory general des surface, V.III, 파리, 1894년
- ^ a b c G. 하멜, 우버 다이 지오메트리엔 데넨 다이 제라덴 다이 커제스틴 신드, 수학앤 57 (1903), 221 - 264.
- ^ a b а. п. п. п. п п п iv п п п п п п п п п п п е е е е е 208 208 208 208 208 208 208 208 208 208 208 р 1 р р р р 1 1 208 208 46 46 46 46 46 46 46 46 46 46 46 46 46 46 46 46 46 46 46 – 46 46 46 46 46 46 46영어 번역: A.V. 포고렐로프, "힐버트의 네 번째 문제, 도클"의 완전한 해결책.Acad. Nauk SSR, Vol. 208, № 1 (1973), 48–52.
- ^ a b А. В. Погорелов, Четвертая Проблема Гильберта.Наука, 1974.영어 번역: A.V. 포고렐로프, 힐버트의 네 번째 문제, 수학에서의 스크립타 시리즈, 윈스턴과 슨, 1979.
- ^ a b R. V. Ambartzumian, 비행기의 유사 메트릭스에 관한 노트, Zeitschrift für Wahrscheinlichtheori und Verwandte Gebiete 1976, 제37권, 제2호, 페이지 145–155
- ^ a b 힐버트, 데이비드, "마테마티슈 푸르메" 괴팅거 나흐리히텐, (1900), 페이지 253–297, 아르키브 데르 수티크 und 피식, (3) 1 (1901), 44–63 및 213–237.Published in English translation by Dr. Maby Winton Newson, Bulletin of the American Mathematical Society 8 (1902), 437–479 [1] [2] doi:10.1090/S0002-9904-1902-00923-3. [A fuller title of the journal Göttinger Nachrichten is Nachrichten von der Königl.게셀샤프트 데르 위스주 괴팅겐.]
- ^ E. Beltrami, Risoluzione del Sublica: Riportare i punti di una superficie sobra in modo le linee geodetiche Vengano rapresentate da line, Annali di Matematea Pura Ed Applitata, №a 7(1865), 185), 185—185204.
- ^ H. 민코프스키, 지오메트리 데어 자일렌, Lpz.-B, 1953.
- ^ D. Hilbert, Uber die gerade Linie als kurzeste Bubindung zweier Punkte, Math.앤, 46세 (1895년), 91-96세.
- ^ L. A. 산탈로 "통합 기하학"In: Global Geometry and Analysis (S. S. Chenger, ed.) Washington, D. C.: 수학.아소크, 아머, 147, 195.
- ^ a b H. Busemann, The Geometry of Geodics, New York, Academic Press, 1955.
- ^ H. Busemann, Review of: A. V. Pogorelov, 힐버트의 네 번째 문제, Bull.아머. 수학.Soc. (N. S.) 제4권, № 1 (1981), 87-90.
- ^ Z. I. Szabo, 힐버트의 네 번째 문제 I, Adv. Math. 59 (1986), 185 - 301.
- ^ R. 알렉산더, 조노이드 이론과 힐버트 네 번째 문제, 검.데디카타 28, № 2 (1988), 199—211.
- ^ J. C. 알바레스 파이바, Symplexic 기하학과 Hilbert 네 번째 문제 J. Different.검. 69, № 2 (2005), 353—378.
- ^ a b J. C. 알바레즈 파비아와 J. 바르보사 곰즈, 힐베르트의 주기적 해결책 네 번째 문제, 20 pp. arXiv:1809.02783v1[math.MG], 2018.
- ^ 파이바, JC 알바레스"힐버트의 네 번째 문제 2차원의." MASS 선택가(2003년): 165–183.
- ^ A. 파파도풀로스, 온 힐버트 네 번째 문제, 1 대 43.힐버트 기하학 핸드북(A. Papadopoulos and M)Troyanov, ed.), 유럽 수학 협회, IRMA 수학 및 이론 물리학 강의, lectures 22 (2014), 페이지 460.
추가 읽기
- Busemann, Herbert (1976). "Problem IV. Desarguesian spaces". In Browder, Felix E. (ed.). Mathematical Developments Arising from Hilbert Problems. Proceedings of Symposia in Pure Mathematics. Vol. XXVIII. American Mathematical Society. pp. 131–141. ISBN 0-8218-1428-1. Zbl 0352.50010.
- Papadopoulos, Athanase (2014). "Hilbert's fourth problem". Handbook of Hilbert geometry (A. Papadopoulos and M. Troyanov, ed.). IRMA Lectures in Mathematics and Theoretical Physics. Vol. 22. European Mathematical Society. pp. 391–432. ISBN 978-3-03719-147-7.



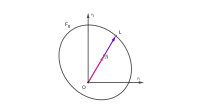








 볼록하며 불규칙할 수 있다.정의된 메트릭은 평탄하다.
볼록하며 불규칙할 수 있다.정의된 메트릭은 평탄하다. 



 제한은
제한은






 Hilbert-Finsler 메트릭
Hilbert-Finsler 메트릭 











 (는)
(는) 



 P 지점을 통과하는 직선의 집합이다.
P 지점을 통과하는 직선의 집합이다.



![{\displaystyle |x,y|=\sigma \left(\tau [x,y]\right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6872ab5eca8f90f7820fe8dbc2abc8b025425bb3)
![{\displaystyle \tau [x,y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b0435a0a01c1fe8c7b5c94a211b11ee5aadba01)
![[x,y]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b7bd6292c6023626c6358bfd3943a031b27d663)













