산술 논리 단위
Arithmetic logic unit| 시리즈의 일부 |
| 산술 논리 회로 |
|---|
| 빠른 네비게이션 |
| 구성 요소들 |
컴퓨팅에서 산술논리유닛(ALU)은 정수 이진수에 [1][2][3]대해 산술연산과 비트연산을 실행하는 조합 디지털 회로입니다.부동소수점수로 동작하는 부동소수점 유닛(FPU)과는 대조적입니다.컴퓨터의 중앙 처리 장치(CPU), FPU, 그래픽 처리 장치(GPU)[4] 등 다양한 유형의 컴퓨팅 회로에 대한 기본 구성 요소입니다.
ALU에 대한 입력은 오퍼랜드라고 불리는 조작 대상 데이터 및 실행할 조작을 나타내는 코드입니다.ALU의 출력은 실행된 조작의 결과입니다.많은 설계에서 ALU는 또한 ALU와 외부 상태 레지스터 간에 각각 이전 동작 또는 현재 동작에 대한 정보를 전달하는 상태 입력 또는 출력 또는 둘 모두를 가진다.
신호.
ALU에는 ALU와 외부 회로 간에 디지털 신호를 전달하는 데 사용되는 전기 도체인 다양한 입력 및 출력 네트가 있습니다.ALU가 동작하고 있는 경우, 외부 회로는 ALU 입력에 신호를 인가하고, ALU는 그 출력을 통해 신호를 생성하여 외부 회로에 전달합니다.
데이터.
기본 ALU는 2개의 입력 오퍼랜드(A, B)와 결과 출력(Y)으로 이루어진 3개의 병렬 데이터 버스를 가진다.각 데이터 버스는 1개의 이진 정수 번호를 전달하는 신호 그룹입니다.일반적으로 A, B 및 Y 버스 폭(각 버스를 구성하는 신호의 수)은 동일하며 외부 회로의 네이티브 워드 크기(예: 캡슐화 CPU 또는 기타 프로세서)와 일치합니다.
오퍼코드
opcode 입력은 ALU에 동작 선택 코드를 전달하는 병렬버스입니다.이것은 ALU에 의해 실행되는 산술 연산 또는 논리 연산을 지정하는 열거치입니다.opcode 크기(버스 폭)에 따라 ALU가 실행할 수 있는 고유 동작의 최대 수가 결정됩니다.예를 들어 4비트의 opcode는 최대 16개의 다른 ALU 동작을 지정할 수 있습니다.일반적으로 ALU opcode는 기계어 opcode와 동일하지 않지만 기계어 opcode 내에서 비트필드로 직접 인코딩되는 경우도 있습니다.
상황
출력
상태 출력은 현재 ALU 작동 결과에 대한 보충 정보를 전달하는 다양한 개별 신호입니다.범용 ALU에는 일반적으로 다음과 같은 상태 신호가 있습니다.
- 반출: 덧셈 연산에 의한 반송, 감산 연산에 의한 차입 또는 바이너리 시프트 연산에 의한 오버플로 비트를 전달합니다.
- 제로: Y의 모든 비트가 로직제로임을 나타냅니다.
- Negative: 산술 연산 결과가 음수임을 나타냅니다.
- 오버플로: 산술 연산의 결과가 숫자 범위인 Y를 초과했음을 나타냅니다.
- 패리티: Y의 짝수 또는 홀수 비트가 로직1인지 여부를 나타냅니다.
각 ALU 연산이 완료되면 상태 출력 신호는 보통 외부 레지스터에 저장되며, 향후 ALU 연산(예를 들어 다중 정밀 산술 구현) 또는 조건부 분기를 제어하기 위해 사용할 수 있습니다.상태 출력을 저장하는 비트 레지스터 컬렉션은 종종 단일 멀티비트 레지스터로 처리되며, 이를 "상태 레지스터" 또는 "상태 코드 레지스터"라고 합니다.
입력
상태 입력을 통해 작업을 수행할 때 ALU에서 추가 정보를 사용할 수 있습니다.일반적으로 이것은 이전 ALU 작업에서 저장된 반출인 단일 "반입" 비트입니다.
회로 동작
ALU는 조합 논리 회로로, 입력 변화에 따라 출력이 비동기적으로 변경됩니다.통상의 동작에서는, 안정된 신호가 모든 ALU 입력에 적용되어 신호가 ALU 회로를 개입시켜 전파되는 데 충분한 시간(「전파 지연」이라고 불린다)이 경과하면, ALU 동작의 결과가 ALU 출력에 표시됩니다.ALU에 접속되어 있는 외부 회로는 동작 전체에서 ALU 입력 신호의 안정성을 확보하고 ALU 결과를 샘플링하기 전에 신호가 ALU를 통해 전파될 때까지 충분한 시간을 허용합니다.
일반적으로 외부 회로는 ALU의 입력에 신호를 가함으로써 ALU를 제어합니다.일반적으로 외부 회로는 시퀀셜 로직을 사용하여 ALU 동작을 제어합니다.이 동작은 ALU 출력이 최악의 상황에서 안정될 때까지 충분한 시간을 확보하기 위해 충분히 낮은 주파수의 클럭 신호에 의해 페이싱됩니다.
예를 들어 CPU는 ALU의 오퍼랜드 입력을 소스(통상 레지스터)에서 ALU의 오퍼랜드 입력으로 라우팅함으로써 ALU의 추가 동작을 시작하고 제어부는 ALU의 opcode 입력에 값을 동시에 적용하여 ALU가 추가를 수행하도록 설정합니다.동시에 CPU는 ALU 결과 출력도 합계를 수신하는 수신처 레지스터에 라우팅합니다.ALU의 입력 신호는 다음 클럭까지 안정적으로 유지되며 CPU가 다음 클럭을 기다리는 동안 ALU와 수신처 레지스터를 통해 전파될 수 있습니다.다음 클럭이 도착하면 수신인 레지스터는 ALU 결과를 저장하고 ALU 동작이 완료되었으므로 다음 ALU 동작을 위해 ALU 입력을 설정할 수 있습니다.
기능들
많은 기본적인 산술 및 비트 논리 함수는 일반적으로 ALU에서 지원됩니다.기본 범용 ALU는 일반적으로 [1][2][3][5]다음 작업을 레퍼토리에 포함합니다.
산술 연산
- 추가: A와 B가 합산되어 Y와 반출에 표시됩니다.
- 캐리와 함께 추가: A, B 및 반입이 합산되고 Y 및 반출 시 합계가 표시됩니다.
- 감산: B는 A에서 감산되고(또는 그 반대), 차이는 Y와 반출에서 나타납니다.이 기능에서 반출은 사실상 "차입" 지표입니다.이 연산은 A와 B의 크기를 비교하기 위해서도 사용할 수 있습니다.이 경우 프로세서에 의해 Y 출력이 무시될 수 있습니다.프로세서는 이 연산에 의해 발생하는 상태 비트(특히 0과 음)에만 관심이 있습니다.
- 차입으로 감산: B는 차입으로 A에서 감산(또는 그 반대)되고 차이는 Y와 반출로 나타납니다.
- 2의 보완(음수):A(또는 B)를 0에서 빼면 차이는 Y에서 나타납니다.
- 증분: A(또는 B)가 1씩 증가하고 결과 값이 Y로 표시됩니다.
- 감소: A(또는 B)는 1 감소하며 결과 값은 Y로 표시됩니다.
- 패스스루: A(또는 B)의 모든 비트는 Y에서 변경되지 않은 것으로 보입니다.이 연산은 일반적으로 피연산자의 패리티 또는 피연산자가 0인지 음인지 여부를 확인하거나 피연산자를 프로세서 레지스터에 로드하는 데 사용됩니다.
비트 논리 연산
- AND: A와 B의 비트 AND는 Y에 표시됩니다.
- OR: A와 B의 비트 OR은 Y에 표시됩니다.
- Exclusive-OR: A와 B의 비트 단위 XOR이 Y에 표시됩니다.
- 1의 보완: A(또는 B)의 모든 비트가 반전되어 Y에 표시됩니다.
비트 시프트 조작
| 유형 | 왼쪽 | 맞다 |
|---|---|---|
| 산술 시프트 |  |  |
| 논리 시프트 |  |  |
| 회전 |  |  |
| 캐리를 통해 회전 |  |  |
ALU 시프트 조작으로 피연산자 A(또는 B)가 (opcode에 따라) 왼쪽 또는 오른쪽으로 시프트하고 시프트된 피연산자가 Y에 표시됩니다.단순 ALU는 일반적으로 피연산자를 1비트 위치만 이동할 수 있는 반면, 더 복잡한 ALU는 피연산자를 한 번의 조작으로 임의의 비트 수만큼 이동할 수 있는 배럴 시프터를 사용합니다.모든 싱글비트 시프트 동작에서 오퍼랜드에서 시프트된 비트는 실행 시 표시됩니다. 오퍼랜드로 시프트된 비트의 값은 시프트 유형에 따라 달라집니다.
- 산술 이동: 피연산자는 2의 보완 정수로 처리되며, 이는 최상위 비트가 "부호" 비트이며 보존됨을 의미합니다.
- 논리적 이동: 논리 0이 피연산자로 이동됩니다.부호 없는 정수를 이동하는 데 사용됩니다.
- 회전: 피연산자는 비트의 원형 버퍼로 처리되므로 피연산자의 최소 및 최대 유효 비트가 효과적으로 인접해 있습니다.
- Rotate through Carry: 캐리 비트와 피연산자는 비트의 원형 버퍼로 일괄 처리됩니다.
적용들
다중 정밀도 산술
정수 연산에서 다중 정밀도 산술은 ALU 워드 크기보다 큰 정수에 대해 연산하는 알고리즘입니다.이를 위해 알고리즘은 각 오퍼랜드를 Most-Significant(MS; 최상위)에서 Last-Significant(LS; 최하위)로 정렬된 ALU 크기의 fragment 집합으로 취급합니다.예를 들어 8비트 ALU의 경우 24비트 정수는0x123456는 3개의 8비트 fragment의 집합으로 취급됩니다.0x12(MS),0x34,그리고.0x56(LS). 조각의 크기가 ALU 단어 크기와 정확히 일치하기 때문에 ALU는 이 피연산자의 "조각"에서 직접 작동할 수 있습니다.
알고리즘은 ALU를 사용하여 특정 피연산자 fragment를 직접 조작하고, 따라서 대응하는 fragment(부분)를 복수 정밀도 결과의 fragment(부분)를 생성합니다.각 부분은 생성될 때 다중 정밀도 결과에 대해 지정된 스토리지의 관련 영역에 기록됩니다.이 처리는 모든 오퍼랜드프래그먼트에 대해 반복되며, 이는 다중 정밀도 연산의 결과인 파셜의 완전한 컬렉션을 생성합니다.
연산(예를 들어 덧셈, 뺄셈)에서 알고리즘은 피연산자의 LS fragment에 대한 ALU 연산을 호출함으로써 LS 부분 및 실행 비트를 모두 생성한다.알고리즘은 지정된 스토리지에 부분적으로 쓰는 반면 프로세서의 상태 머신은 일반적으로 실행 비트를 ALU 상태 레지스터에 저장합니다.그 후 알고리즘은 각 오퍼랜드 컬렉션의 다음 단편으로 진행되며 이전 ALU 연산에서 저장된 캐리 비트와 함께 이들 단편에서 ALU 연산을 호출하여 다른 (더 중요한) 부분 및 실행 비트를 생성합니다.종래와 같이 상태 레지스터에 캐리 비트를 격납하고, 그 일부를 지정된 격납장치에 쓴다.이 프로세스는 모든 피연산자 fragment가 처리될 때까지 반복되며, 결과적으로 스토리지 내의 파셜이 완전히 수집되어 다중 정밀도 산술 결과를 구성합니다.
다중 정밀도 시프트 동작에서는 피연산자 fragment 처리의 순서는 시프트 방향에 따라 달라집니다.왼쪽 시프트 동작에서는 각 부분(저장된 캐리 비트를 통해 전송됨)의 LS 비트는 이전에 왼쪽 시프트된 덜 중요한 피연산자의 MS 비트로부터 취득해야 하기 때문에 fragment가 먼저 LS 처리됩니다.반대로 각 부분의 MS 비트는 이전에 오른쪽 시프트된 보다 중요한 피연산자의 LS 비트로부터 취득해야 하기 때문에 피연산자는 오른쪽 시프트 동작에서 먼저 MS가 처리됩니다.
비트 단위 논리 연산(예를 들어 논리 AND, 논리 OR)에서 피연산자 fragment는 각 파셜이 대응하는 피연산자 fragment에만 의존하기 때문에 임의의 순서로 처리될 수 있다(이전 ALU 연산으로부터의 기억된 캐리 비트는 무시된다).
복잡한 운용
ALU는 복잡한 기능을 수행하도록 설계할 수 있지만, 결과적으로 회로 복잡성, 비용, 전력 소비 및 대규모로 인해 많은 경우 실용적이지 않습니다.따라서 ALU는 종종 매우 빠른 속도로 실행할 수 있는 단순한 기능(즉, 매우 짧은 전파 지연)으로 제한되며, 외부 프로세서 회로는 일련의 단순한 ALU 연산을 조정함으로써 복잡한 기능을 수행합니다.
예를 들어 ALU의 복잡도에 따라 숫자의 제곱근 계산은 다양한 방법으로 구현될 수 있습니다.
- 1개의 클럭으로 계산: 1개의 연산으로 제곱근을 계산하는 매우 복잡한 ALU.
- 계산 파이프라인: ALU를 통과하는 중간 결과가 공장 생산 라인처럼 배치되어 있는 단계별로 제곱근을 계산하는 단순 ALU 그룹입니다.이 회로는 이전 피연산자를 완료하기 전에 새로운 피연산자를 받아들일 수 있으며 매우 복잡한 ALU만큼 빠르게 결과를 얻을 수 있습니다.단, 결과는 ALU 스테이지의 전파 지연의 합계에 의해 지연됩니다.자세한 내용은 명령 파이프라인에 대한 문서를 참조하십시오.
- 반복 계산: 제어 유닛의 지시에 따라 여러 단계를 거쳐 제곱근을 계산하는 간단한 ALU.
위의 구현은 가장 빠르고 비용이 많이 드는 구현에서 가장 느리고 비용이 적게 드는 구현으로 전환됩니다.제곱근은 모든 경우에 계산되지만 단순 ALU를 사용하는 프로세서는 여러 ALU 연산을 수행해야 하므로 계산 수행에 시간이 오래 걸립니다.
실행
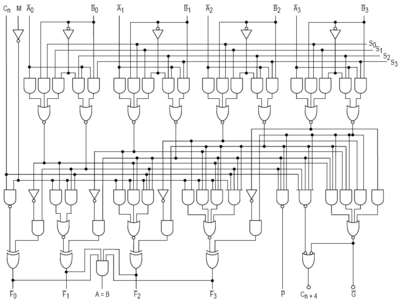
ALU는 보통 74181과 같은 독립형 집적회로(IC) 또는 보다 복잡한 IC의 일부로 구현됩니다.후자의 경우 ALU는 일반적으로 VHDL, Verilog 또는 기타 하드웨어 기술 언어로 작성된 기술에서 ALU를 합성함으로써 인스턴스화됩니다.예를 들어, 다음 VHDL 코드는 매우 단순한 8비트 ALU를 나타냅니다.
독립체 알루 이 항구 ( -- 외부 회로에 대한 alu 연결: A : 에 서명된(7 까지 0); -- 오퍼랜드 A B : 에 서명된(7 까지 0); -- 오퍼랜드 B 동작 : 에 서명되어 있지 않다(2 까지 0); --opcode Y : 나가. 서명된(7 까지 0)); -- 작업 결과 끝. 알루; 아키텍처 동작의 의 알루 이 시작한다. 사례. 동작 이 -- opcode를 디코딩하고 다음 작업을 수행합니다. 언제 "000" => Y <=> A + B; --추가 언제 "001" => Y <=> A - B; -- 뺄셈 언제 "010" => Y <=> A - 1; --감소 언제 "011" => Y <=> A + 1; -- 증분 언제 "100" => Y <=> 것은 아니다. A; -- 1의 보완물 언제 "101" => Y <=> A 그리고. B; -- 비트 AND 언제 "110" => Y <=> A 또는 B; -- 비트 단위 OR 언제 "111" => Y <=> A xor B; -- 비트 단위 XOR 언제 다른이들 => Y <=> (다른이들 => 'X'); 끝. 사례.; 끝. 동작의; 역사
수학자 존 폰 노이만은 1945년 EDVAC라고 불리는 [6]새로운 컴퓨터의 기초에 대한 보고서에서 ALU 개념을 제안했다.
전자회로의 비용, 크기 및 소비전력은 정보화 시대 초기 내내 상대적으로 높았습니다.그 결과, 모든 시리얼 컴퓨터와 PDP-8과 같은 많은 초기 컴퓨터들은 프로그래머들에게 더 넓은 워드 크기를 제공하긴 했지만, 한 번에 하나의 데이터 비트로 작동하는 단순한 ALU를 가지고 있었다.여러 개의 개별 단일 비트 ALU 회로를 갖춘 최초의 컴퓨터 중 하나는 1948년 Wirlwind I로, 16비트 단어로 작동하기 위해 16개의 "수학 단위"를 사용했습니다.
1967년 Fairchild는 집적회로로서 구현된 최초의 ALU인 Fairchild 3800을 도입했습니다.Fairchild 3800은 축전지 [7]8비트의 ALU로 구성되어 있습니다.Am2901 및 74181과 같은 4비트 ALU를 포함한 다른 집적회로 ALU가 곧 등장했습니다.이 장치들은 일반적으로 "비트 슬라이스"가 가능했습니다. 즉, 서로 연결된 여러 개의 ALU 칩을 사용하여 더 넓은 워드 크기의 ALU를 만들 수 있는 "carry look ahead" 신호를 가지고 있었습니다.이 장치들은 빠르게 대중화되었고 비트슬라이스 미니컴퓨터에 널리 사용되었다.
마이크로프로세서는 1970년대 초에 등장하기 시작했다.트랜지스터가 작아졌음에도 불구하고, 종종 완전한 단어 폭의 ALU를 위한 다이 공간이 부족했고, 그 결과 일부 초기 마이크로프로세서는 기계어 명령당 여러 사이클이 필요한 좁은 ALU를 사용했습니다.그 예로는 4비트의 [8]ALU를 사용하여 8비트를 추가한 Zilog Z80이 있습니다.시간이 지남에 따라 트랜지스터의 형상은 무어의 법칙에 따라 더욱 축소되어 마이크로프로세서에 보다 넓은 ALU를 구축할 수 있게 되었습니다.
현대의 집적회로(IC) 트랜지스터는 초기 마이크로프로세서보다 크기가 작기 때문에 매우 복잡한 ALU를 IC에 장착할 수 있습니다.오늘날 많은 현대 ALU는 단어 폭이 넓고 배럴 시프터 및 바이너리 멀티플라이어와 같은 아키텍처가 개선되어 이전 ALU에서 여러 번의 연산이 필요했던 연산을 단일 클럭 사이클로 실행할 수 있습니다.
ALU는 기계 회로, 전기 기계 회로 또는 전자[9][failed verification] 회로로 실현될 수 있으며, 최근에는 생물학적 ALU에 대한 연구(예: 액틴 기반)[12]가 수행되고[10][11] 있다.
「 」를 참조해 주세요.
레퍼런스
- ^ a b A.P.Godse; D.A.Godse (2009). "3". Digital Logic Design. Technical Publications. pp. 9–3. ISBN 978-81-8431-738-1.
- ^ a b Leadership Education and Training (LET) 2: Programmed Text. Headquarters, Department of the Army. 2001. pp. 371–.
- ^ a b A.P.Godse; D.A.Godse (2009). "Appendix". Digital Logic Circuits. Technical Publications. pp. C–1. ISBN 978-81-8431-650-6.
- ^ "1. An Introduction to Computer Architecture - Designing Embedded Hardware, 2nd Edition [Book]". www.oreilly.com. Retrieved 2020-09-03.
- ^ Horowitz, Paul; Winfield Hill (1989). "14.1.1". The Art of Electronics (2nd ed.). Cambridge University Press. pp. 990–. ISBN 978-0-521-37095-0.
- ^ Philip Levis (November 8, 2004). "Jonathan von Neumann and EDVAC" (PDF). cs.berkeley.edu. pp. 1, 3. Archived from the original (PDF) on September 23, 2015. Retrieved January 20, 2015.
- ^ Lee Boysel (2007-10-12). "Making Your First Million (and other tips for aspiring entrepreneurs)". U. Mich. EECS Presentation / ECE Recordings. Archived from the original on 2012-11-15.
- ^ 켄 쉬리프."Z-80은 4비트 ALU를 탑재하고 있습니다.이렇게 동작합니다." 2013, righto.com
- ^ Reif, John H. (2009), "Mechanical Computing: The Computational Complexity of Physical Devices", in Meyers, Robert A. (ed.), Encyclopedia of Complexity and Systems Science, New York, NY: Springer, pp. 5466–5482, doi:10.1007/978-0-387-30440-3_325, ISBN 978-0-387-30440-3, retrieved 2020-09-03
- ^ Lin, Chun-Liang; Kuo, Ting-Yu; Li, Wei-Xian (2018-08-14). "Synthesis of control unit for future biocomputer". Journal of Biological Engineering. 12 (1): 14. doi:10.1186/s13036-018-0109-4. ISSN 1754-1611. PMC 6092829. PMID 30127848.
- ^ Gerd Hg Moe-Behrens. "The biological microprocessor, or how to build a computer with biological parts".
- ^ Das, Biplab; Paul, Avijit Kumar; De, Debashis (2019-08-16). "An unconventional Arithmetic Logic Unit design and computing in Actin Quantum Cellular Automata". Microsystem Technologies. doi:10.1007/s00542-019-04590-1. ISSN 1432-1858. S2CID 202099203.
추가 정보
- Hwang, Enoch (2006). Digital Logic and Microprocessor Design with VHDL. Thomson. ISBN 0-534-46593-5.
- Stallings, William (2006). Computer Organization & Architecture: Designing for Performance (7th ed.). Pearson Prentice Hall. ISBN 0-13-185644-8.