동위 원소형
Isotoxal figure기하학에서 폴리토프(예를 들어 폴리곤 또는 다면체) 또는 타일링은 그것의 대칭이 그것의 가장자리에서 전이적으로 작용하는 경우 동위원소 또는 에지 변환이다. 비공식적으로, 이것은 물체에 하나의 가장자리 유형만 있다는 것을 의미한다: 두 개의 가장자리가 주어진다면, 물체가 점유한 지역을 변경하지 않고 한 가장자리를 다른 가장자리로 이동하는 번역, 회전 및/또는 반사가 있다.
동위원소라는 용어는 호를 의미하는 그리스어 τόξν에서 유래되었다.
동위원소 폴리곤
동위원소 폴리곤은 균일한 면의 등각 폴리곤이지만, 모든 등각 폴리곤이 동위원소인 것은 아니다. 동위원소 폴리곤의 이중은 등각 폴리곤이다. 4n-곤은 중앙 대칭이므로 조노곤도 있다.
일반적으로 동위원소 2n-곤은 Dn(*n) 이면 대칭을 가진다. rhombus는 D2(*22) 대칭을 갖는 동위원소 폴리곤이다. 모든 정규 다각형(등각 삼각형, 정사각형 등)은 동위원소로서 최소 대칭 순서의 두 배가 된다: 일반 n-곤은 Dn(*n) 이면 대칭이 있다.
동위원소 2n-곤은 바깥쪽 가장 내부 각도가 α인 {nα}이라고 라벨을 붙일 수 있다. 두 번째 내부 각도 β는 볼록하거나 오목한 다각형을 만들면서 180도보다 크거나 작을 수 있다. 또한 별 폴리곤은 q<n-1과 gcd(n,q)=1을 가진 동위원소({(n/q)})α로, q를 회전수 또는 밀도로 사용할 수 있다.[1] 오목한 내부 정점은 q<n/2>에 대해 정의할 수 있다. a와 같이 가장 큰 공통점이 있는 경우 {(na/qa)}α을(를) 복사된 회전으로 화합물 a{(n/q)}α로 줄일 수 있다.
균일한 기울기 세트는 동위원소 폴리곤으로 보다 낮은 유형의 정규 면으로 정의할 수 있다.
| 면(2n) | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
|---|---|---|---|---|---|---|---|
| {nα} 볼록 β<180 오목 β>180 | {2α} |   {3α} |   {4α} |   {5α} |   {6α} |   {7α} |   {8α} |
| 2회전 {(n/2)α} | -- |  {(3/2)α} |  2{2α} | 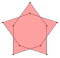  {(5/2)α} |   2{3α} |   {(7/2)α} |   2{4α} |
| 3회전 {(n/3)α} | -- | -- |  {(4/3)α} |  {(5/3)α} |  3{2α} |   {(7/3)α} |   {(8/3)α} |
| 4회전 {(n/4)α} | -- | -- | -- |  {(5/4)α} |  2{(3/2)α} |  {(7/4)α} |  4{2α} |
| 5회전 {(n/5)α} | -- | -- | -- | -- |  {(6/5)α} |  {(7/5)α} |  {(8/5)α} |
| 6회전 {(n/6)α} | -- | -- | -- | -- | -- |  {(7/6)α} |  2{(4/3)α} |
| 7회전 {(n/7)α} | -- | -- | -- | -- | -- | -- |  {(8/7)α} |
동위원소 다면체 및 기울기
일반 다면체는 등면체(얼굴-변환), 이소곤체(Vertex-변환), 동위원소(에지-변환)이다.
큐오크타헤드론이나 이코시다데카헤드론처럼 퀘이레곤 다면체는 등면체 및 동위원소지만 등면체는 아니다. Rhombic 도데카헤드론과 Rhombic 3권각체(Rhombic dodecheadron), Rhombic 3권각체(Rhombic triacontahedron)를 포함한 이들의 이중은 등면체 및 동위원소(Is
| 퀘이레굴라속 다면체 | 쿼이레겔러 이중 다면체 | 퀘이레굴라속 별 다면체 | 쿼이레겔러 이중 별 다면체 | 퀘이레굴라속 타일링 | 쿼이레겔러 이중 타일링 |
|---|---|---|---|---|---|
 큐옥타헤드론은 이산화 및 동위원소 다면체다. |  Rhombic dodecheadron은 등면체 및 동위원소 다면체다면체다면체 |  위대한 이코시다데카헤드론은 이소질 및 동위원소 항성 다면체다. |  대범한 삼정삼면체(大 rh三面)는 등면체(등면체)와 동위원소 별 다면체(東方體)이다. |  3헥사각 타일링은 이소각 및 동위원소 타일링이다. |  롬빌 타일링은 p6m(*632) 대칭이 있는 등면 및 동위원소 타일링이다. |
일반 폴리곤으로 구성된 모든 다면체나 2차원 테셀레이션이 동위원소인 것은 아니다. 예를 들어 잘린 이코사헤드론(익숙한 축구공)은 육각-헥사곤과 육각-펜타곤의 두 가지 가장자리 유형을 가지고 있으며, 육각-헥사곤 가장자리를 육각-펜타곤 가장자리로 이동하는 고체의 대칭은 불가능하기 때문에 동위원소성이 아니다.
동위원소 다면체는 모든 가장자리에서 동일한 이면각을 가진다.
볼록 다면체의 이중도 역시 볼록 다면체다.[2]
비콘벡스 다면체의 이중도 역시 비콘벡스 다면체다.[2] (대립에 의해)
동위원소 다면체의 이중도 역시 동위원소 다면체다.(이중 다면체 기사 참조)
볼록 동위원소 다면체에는 5개의 (정규) 플라토닉 고형물, 2개의 이중 플라토닉 고형물의 공통 코어(정규)와 2개의 듀얼이 있다.
비콘벡스 동위원소 다면체는 14개로 이중 케플러-Poinsot 다면체, 이중 케플러-Poinsot 다면체의 공통 코어 2개와 그 이중 2개에 4개의 4개의 4개의 4개의 4개의 4개의 4개의 4개의 4개의 4개의 2개의 2개의 2개의 2개의 2개의 2개의 2개의 2개의 2개의 2개의 2개의 2개의 2개의 2개의 2개의 2개의 2개의 2개의 2개의 2개의 항성체면체면체면체가 있다.
최소 5개의 동위원소 다면 화합물이 있다: 5개의 정규 다면 화합물; 5개의 이중화합물 또한 5개의 정규 다면화합물이다.
유클리드 평면의 동위원소 폴리곤 기울기가 최소 5개 있고, 쌍곡면의 동위원소 폴리곤 기울기가 무한히 많으며, 여기에는 일반 쌍곡선 기울기 {p,q} 및 비우측(p q r) 그룹의 와이토프 구조물이 포함된다.
참고 항목
참조
- 피터 R. Cromwell, Polyhedra, Cambridge University Press 1997, ISBN 0-521-55432-2, 페이지 371 Transitivity
- Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. New York: W. H. Freeman. ISBN 0-7167-1193-1. (6.4 동위원소 기울기, 309-321)
- Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954), "Uniform polyhedra", Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences, 246 (916): 401–450, Bibcode:1954RSPTA.246..401C, doi:10.1098/rsta.1954.0003, ISSN 0080-4614, JSTOR 91532, MR 0062446, S2CID 202575183


