잠재 디리클레 할당

이 기사는 대부분의 독자들이 이해하기에는 너무 전문적일 수 있다. 기술적인 세부사항을 삭제하지 않고 비전문가도 쉽게 이해할 수 있도록 개선해주시기 바랍니다. (2017년 8월) (이 템플릿 메시지 삭제 방법 및 삭제 시기 확인)

자연어 처리에서 잠재 디리클레 할당(LDA)은 관찰되지 않은 그룹을 통해 관측치 집합을 설명하는 생성 통계 모델이며, 각 그룹은 데이터의 일부 부분이 유사한 이유를 설명합니다.LDA는 주제 모형의 예입니다.여기서 관찰(예: 단어)은 문서로 수집되고 각 단어의 존재는 문서의 주제 중 하나에 기인합니다.각 문서에는 소수의 주제가 포함되어 있습니다.

역사

집단 유전학의 맥락에서 LDA는 J. K. 프리처드, M. 스티븐스, P에 의해 제안되었다. 2000년에 ^[1][2]도넬리.

LDA는 2003년 ^[3]David Blei, Andrew Ng 및 Michael I. Jordan에 의해 기계학습에 적용되었습니다.

개요

진화생물학과 바이오의학

진화생물학과 바이오의학에서 모델은 개인의 집단에서 구조화된 유전자 변이의 존재를 감지하기 위해 사용된다.이 모델은 연구 대상 개인이 가지고 있는 대립 유전자가 다양한 현존 또는 과거 집단에서 기원한다고 가정한다.모델과 다양한 추론 알고리즘은 과학자들이 연구 대상 개체군의 대립 유전자의 빈도와 연구 대상 개체들이 가지고 있는 대립 유전자의 기원을 추정할 수 있게 해준다.선원 모집단은 다양한 진화 시나리오의 관점에서 사후 해석될 수 있다.연합 연구에서 유전자 구조의 존재를 감지하는 것은 교란 요인을 피하기 위해 필요한 예비 단계로 간주된다.

기계 학습

머신러닝에서의 LDA의 응용 프로그램 중 하나는, 특히 토픽 검출, 자연어 처리의 서브 문제 등입니다.이러한 토픽은 문서 컬렉션 내의 토픽을 검출하고, 검출된 각 토픽에 대한 「관련」의 관점에서, 컬렉션내의 개개의 문서를 자동적으로 분류하는 것입니다.주제는 하나의 용어 집합(즉, 개별 단어 또는 구)으로 간주되며, 함께 취합되어 공유 주제를 제안합니다.

예를 들어 애완 동물과 관련된 문서 컬렉션에서 dog, spaniel, beagle, golden retriver, puppy, bark, woof라는 용어는 DOG_ 관련 테마를 제안하고 cat, siamese, maine coon, tabbby, manx, 야옹, purr 및 kitten이라는 용어는 CAT_ 관련 테마를 제안합니다.컬렉션에는 단순함을 위해 논의하지 않는 다이어트, 몸단장, 의료, 행동 등과 같은 더 많은 주제가 있을 수 있습니다.(예를 들어 "the", "an", "that", "are", "is" 등 언어에서 정지어라고 불리는 매우 일반적인 단어는 주제를 구분하지 않으며 보통 LDA가 수행되기 전에 사전 처리를 통해 걸러진다.또한 전처리는 용어를 "근원" 어휘 형식으로 변환합니다. 예를 들어 "barks", "barking", "barked"는 "barked"는 "bark"로 변환됩니다).

문서 수집이 충분히 큰 경우, LDA는 개별 주제에 의미 있는 라벨을 할당하는 작업(즉, 모든 용어가 DOG_관련)은 사용자의 몫이며 종종 수집에 대한 전문 지식(예, 주제)을 필요로 하지만 개별 용어의 공존에 기초하여 그러한 용어 집합을 발견한다.기술 문서)를 참조해 주세요.LDA 접근방식은 다음과 같이 가정한다.

1. 문서의 의미적 내용은 하나 이상의 주제에서 하나 이상의 용어를 결합하여 구성됩니다.
2. 어떤 용어는 애매하고, 여러 주제에 속하며, 다른 가능성을 가지고 있다. (예를 들어, 훈련이라는 용어는 개와 고양이 모두에게 적용될 수 있지만, 개를 지칭하는 경우가 더 많다. 그들은 일하는 동물로 쓰이거나 복종이나 기술 경쟁에 참가한다.)단, 문서에서는 특정 인접 용어(하나의 토픽에만 속하는 용어)가 함께 존재하면 용법이 명확해집니다.
3. 대부분의 문서에는 비교적 적은 수의 주제만 포함되어 있습니다.예를 들어, 컬렉션에서 개별 토픽은 다른 빈도로 발생합니다.즉, 확률 분포를 가지므로 특정 문서가 다른 문서보다 일부 주제를 포함할 가능성이 높습니다.
4. 주제 내에서 특정 용어는 다른 용어보다 훨씬 더 자주 사용됩니다.즉, 항목 내의 항에도 자체 확률 분포가 있습니다.

LDA 기계 학습을 사용할 때, 베이지안 방법과 기대 최대화 알고리즘을 사용하여 훈련 단계 동안 확률의 두 세트가 모두 계산된다.

LDA는 확률론적 잠재의미분석(pLSA)의 오래된 접근방식의 일반화이다. pLSA 모델은 균일한 디리클레 사전 분포 ^[4]하에서의 LDA와 동일하다. pLSA는 위의 처음 두 가정에만 의존하며 나머지는 신경 쓰지 않는다.두 방법 모두 원칙적으로 유사하며 사용자가 훈련을 시작하기 전에 검색할 주제 수를 지정해야 하지만(K-평균 클러스터링과 마찬가지로) LDA는 pLSA에 비해 다음과 같은 이점이 있습니다.

• LDA는 단어를 더 잘 명확하게 하고 주제에 문서를 더 정확하게 할당할 수 있습니다.
• 확률 계산은 원래 수집의 통계적 특성을 밀접하게 반영하는 새로운 "합성 문서" 수집을 생성할 수 있는 "생성적" 프로세스를 가능하게 한다.
• LDA와 달리 pLSA는 특히 말뭉치의 크기가 증가할 때 과적합에 취약하다.
• LDA 알고리즘은 컴퓨팅 클러스터의 MapReduce 접근방식을 사용하여 대규모 데이터 세트를 쉽게 확장할 수 있습니다.

모델

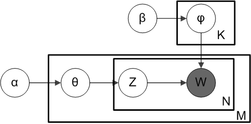
확률론적 그래픽 모델(PGM)을 나타내는 데 자주 사용되는 플레이트 표기법을 사용하면 여러 변수 간의 의존성을 간결하게 포착할 수 있다.상자는 반복된 도면요소인 반복실험을 나타내는 "플레이트"입니다.바깥쪽 판은 문서를 나타내며 안쪽 판은 주어진 문서에서 반복되는 단어 위치를 나타냅니다. 각 위치는 주제 및 단어 선택과 관련이 있습니다.변수 이름은 다음과 같이 정의됩니다.

M은 문서 수를 나타냅니다.

N은 특정 문서 내의 단어 수(문서 i에는 $(\$}) 단어가$$ $있습니다{\displaystyle {}_{}}$)

α는 문서별 주제 분포에 앞서 Dirichlet의 매개변수이다.

β는 주제별 단어 분포 이전의 Dirichlet 매개변수이다.

$§$ $i(\displaystyle\theta_{$i$$})는 문서 i의 토픽 배포입니다.

$§$ $k(\displaystyle$ \$varphi _{$k$$$})$는 토픽 k의 단어 분포입니다.

${\displaystyle z_{}}$ ${\displaystyle i_{}}$j(\$displaystyle z_{ij})$는 문서 i의 j번째 단어의 주제입니다.

${\displaystyle w_{}}$ i$$ { $display$ style $w$_ { $ij$} ${\displaystyle w_{}}$ w 。

W가 회색으로 표시되어 있다는 것은 ${\displaystyle {wi}_{}}$ $(\$ 단어만이$$ 관측 가능한 변수이고 다른 변수는 잠재 변수임을 의미합니다.원본 ^[3]논문에서 제안했듯이, 주제의 단어에 대한 확률 분포가 왜곡되어 소수의 단어 세트만 높은 확률을 갖는다는 직관에 따라, 희소 디리클레를 사용하여 주제-단어 분포를 모델링할 수 있다.결과 모델은 현재 가장 널리 적용되는 LDA 변형입니다.이 모델의 플레이트 표기법은 오른쪽에 표시되어 있습니다.$K{\displaystyle }$${\displaystyle \{\backslash }$$displaystyle$K }는${\displaystyle }$토픽의 수를 나타내고 있습니다.K${$ displaystyle $\varphi _{$1} \$dots$, \$varphi _{$K$$}는 디리클레 분산된 토픽의 파라미터를 저장하는 V$${\$displaystyle$ V$}$차원$$ $$입니다.$ystyle$ V$}$는 어휘의 단어 수입니다).

$【\displaystyle \theta】$와 $【\displaystyle \varphi】$로 표현되는 엔티티는 모델링되는 문서의 말뭉치를 나타내는 원래의 문서-워드 매트릭스를 분해하여 작성된 매트릭스라고 생각하면 도움이 됩니다.$이{\displaystyle }$ 뷰에서 ${\$ { $displaystyle \theta$}는$$ 문서와 토픽으로 정의된 열로 구성되며, ${\$ { \ $displaystyle$\ $varphi$}는 토픽으로 정의된 열과 단어로 정의된 열로 구성됩니다.${\displaystyle {따라서\mathrm{}}_{}}$ "$1{\displaystyle {}_{}\dots ",}$ "${\displaystyle K_{}}$\$displaystyle \varphi _{1},\dots",$ "\$varphi _{$K$$}"는 각각 단어에 대한 분포인 행 또는 벡터 집합을 나타내며$,$ "1, ${\displaystyle ...",}$ "${\displaystyle M_{}}$\$display$ style $\theta _{1$},\$dots,\ta$ _${M$}}"는$$ 각 행 집합을 나타냅니다.

생성 과정

실제로 말뭉치 내의 주제를 추론하기 위해 우리는 문서가 생성되는 생성 과정을 상상하고, 이를 추론하거나 역설계할 수 있습니다.우리는 그 생성 과정을 다음과 같이 상상한다.문서는 잠재 주제에 대한 무작위 혼합으로 표현되며, 각 주제는 모든 단어에 대한 분포로 특징지어집니다.LDA는 각각 ${\displaystyle {길이}_{}}$ Ni$({$i$\})$의$$M개의 문서({$displaystyle$M})로 구성된$$ $말뭉치{\displaystyle }$D(\$displaystyle$ D$)$에 대해 다음과 같은 생성 프로세스를 가정한다.

1. ${\displaystyle i_{}}$~ ${\displaystyle \mathrm{Dir}}$ ${\displaystyle (}$ (${\displaystyle }$α$$) \ $displaystyle \theta$ { $i$} \$sim$ \$operatorname${$Dir$}$$( \ $alpha$)를$$ 선택합니다.${\displaystyle \mathrm{여기}}$서 i ${\displaystyle \{}$ 1${\displaystyle }$, ${\displaystyle ...}$ , M$}$ { $displaystyle$i \ $in$ \$1$ , \$dots$,$M$ \ $}$ 、 ${\displaystyle \mathrm{Dir<img\; alt="i\backslash in\; \backslash \{1,\backslash dots\; ,M\backslash \}"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/e3c343e4a3e656e75d8e4e47c9d623a4beff6ad7"\; style="vertical-align:\; -0.838ex;\; width:14.751ex;\; height:2.843ex;">}}$ \ $display$ style \ dots \ $mathrm${$dir$ $）$} ） 。e (< \ $displaystyle \alpha$$< 1$)

$2{\displaystyle {}_{}}$. [${\displaystyle {}_{}}$] k ~ [ ${\displaystyle \mathrm{Dir}}$ ${\displaystyle ]}$ ($β$) \$displaystyle$ \ $varphi$_ { k } \ $sim \operatorname$ { Dir$$$}$ ( \$beta$ )$$]를 선택합니다.$여기$서 k ${\displaystyle \{}$ { ${\displaystyle 1}$, $...$, $}$ { $displaystyle$$$k$\$$in$ \ { 1, \$dots$ ,$$K\} 및$$}는 일반적으로 sparse입니다.

3. 각 단어 $위치{\displaystyle }$ i$, j$${\displaystyle \mathrm{여기}}$서 i $i{\displaystyle }$ { ${\displaystyle 1}$, ${\displaystyle ...}$,${\displaystyle }$M $}$ { $displaystyle$i \ $in$ \$1,$ $\ dots$ , ${\displaystyle {}_{}}$$$\$$} , $j{\displaystyle }$ ${\displaystyle \{}$ {${\displaystyle 1}$, ...${\displaystyle }$, ${\displaystyle N_{}}$ i $}$ { $displaystyle$j \ $in$\$$1$,$ \ $dots$, N$i }$ ) 。

(a) $항목{\displaystyle {}_{}}$ ${\displaystyle z_{}}$ i${\displaystyle {,}_{}}$ ${\displaystyle j_{}}$~ ${\displaystyle \mathrm{다항식}}$ ( ${\displaystyle i_{}}$i )${\displaystyle }$.$${ $displaystyle z_{i,j}\sim \operatorname {Multinal}(\theta$ _${i})$을 선택합니다.$}$

(b) 단어 ${\displaystyle w_{}}$ i${\displaystyle {,}_{}{j}_{}}$ ~ ${\displaystyle \mathrm{다항식}(}$ ( ${\displaystyle {z{}_{}}_{}}$ z${\displaystyle {i_{}}_{}}$ ,${\displaystyle {{}_{}}_{}{j_{}}_{}}$) .$${ $displaystyle w_{i$ , j$}\sim \operatorname${ $Multinodanal }$ ( \ $varphi _$ { $z$_ {$i$ , $j}$ )를 선택합니다.$}$

(여기서 다항 분포는 범주형 분포라고도 하는 시행이 하나만 있는 다항 분포를 가리킵니다.)

$길이{\displaystyle {}_{}}$ $(\$는 다른 모든 데이터 생성 변수$(\displaystyle$ w$$$)$ 및$z{\displaystyle }$(\$displaystyle$ z$)$와는 무관한 것으로 취급됩니다.여기에 표시된 플레이트 다이어그램과 같이 첨자가 자주 떨어집니다.

정의.

LDA에 대한 공식적인 설명은 다음과 같습니다.

모형의 변수 정의

변수	유형	의미.
${\displaystyle K}$	정수	주제 수(예: 50)
${\displaystyle V}$	정수	어휘의 단어 수(예: 50,000 또는 100,000)
${\displaystyle M}$	정수	문서수
${\displaystyle N_{d=1\dots M}}$	정수	문서 d의 단어 수
${\displaystyle N}$	정수	모든 문서의 총 단어 수: 모든 $N{\displaystyle {}_{}}$ { $displaystyle$ $N$$$_ { $d$} ${\displaystyle =}$ $1{\displaystyle }$ ${\displaystyle M_{}}$ N d$=$ \ $sum$_ { d$$=$1$}^{$M _$ { $d$} } N _ { d } 。
${\displaystyle \alpha _{k=1\display K}}$	정의 실수	문서의 주제 k의 이전 가중치. 일반적으로 모든 주제에 대해 동일하며, 일반적으로 1보다 작은 숫자(예: 0.1)는 희박한 주제 분포를 선호한다. 즉, 문서당 몇 개의 주제
$(\displaystyle\boldsymbol\alpha })$	양의 실수의 K차원 벡터	$모든{\displaystyle {}_{}}$ ${\displaystyle {\alpha }_{}}$ k$(\$ _${k})$ 값$$ 집합, 단일 벡터로 표시
$\displaystyle \display_{w=1\display V}$	정의 실수	토픽에서 단어 w의 이전 가중치. 보통 모든 단어에 대해 동일하며, 일반적으로 1보다 훨씬 적은 수(예: 0.001)는 희박한 단어 분포를 강하게 선호한다. 즉, 주제당 단어 수
$(*displaystyle\boldsymbol\class})$	양의 실수의 V차원 벡터	$모든{\displaystyle {}_{}}$ ${\displaystyle {\beta }_{}}$ w$$\ $displaystyle$\ $display$ style _ { $w$} 값$$ 집합, 단일 벡터로 표시
$\displaystyle \varphi _{k=1\dots K,w=1\dots V}$	확률(0과 1) 사이의 실수	항목 k에서 단어 w가 발생할 확률
$(\displaystyle\boldsymbol\varphi}}_{k=1\displayK})$	확률의 V차원 벡터. 합계는 1이어야 합니다.	토픽 k의 단어 분포
$\displaystyle \theta _{d=1\dots M,k=1\dots K}$	확률(0과 1) 사이의 실수	문서 d에서 주제 k가 발생할 확률
$(\displaystyle\boldsymbol\theta\}_{d=1\displayM})$	K차원 확률 벡터, 합계는 1이어야 합니다.	문서 d의 주제 분포
${\displaystyle z_{d=1\dots M,w=1\dots N_{d}}$	1과 K 사이의 정수	문서 d의 단어 w의 주제 동일성
${\displaystyle\mathbf {Z}$	1과 K 사이의 정수의 N차원 벡터	모든 문서에서 모든 단어의 주제 동일성
$({displaystyle w_{d=1\dots M,w=1\dots N_{d}})$	1과 V 사이의 정수	문서 d의 단어 w의 동일성
$\displaystyle \mathbf {W}$	1과 V 사이의 정수의 N차원 벡터	모든 문서에 포함된 모든 단어의 동일성

그런 다음 랜덤 변수를 다음과 같이 수학적으로 설명할 수 있습니다.

${\displaystyle {\boldsymbol {varphi }}_{k=1\sim K}&\sim \operatorname {Dirichlet}_{V}(\boldsymbol {theta }}}_{\boldsimbol {d =1\m}}\opericlet M}_{V}\sim Dirame }\\w_{d=1\dots M,w=1\dots N_{d}}&\sim \operatorname {Categoryical}_{V}({\boldsymbol {varphi }}}_{z_{narg}})\end{aligned}}}$

추론

다양한 분포(주제의 집합, 연관된 단어 확률, 각 단어의 주제 및 각 문서의 특정 주제 혼합)를 배우는 것은 통계적 추론의 문제이다.

몬테카를로 시뮬레이션

Pritchard ^[1]등의 오리지널 논문.몬테카를로 시뮬레이션에 의한 후방 분포의 근사치를 사용했다.추론 기법의 대안적 제안에는 깁스 ^[5]표본 추출이 포함된다.

변이 베이즈

원래의 ML 논문은 후방 ^[3]분포의 변형 베이즈 근사치를 사용했다.

우도 최대화

블록 완화 알고리즘을 사용하여 우도를 직접 최적화하는 것이 MCMC의 ^[6]빠른 대안임을 증명한다.

모집단/토픽 수를 알 수 없습니다.

실제로 최적의 모집단 또는 주제 수는 사전에 알려져 있지 않습니다.이는 가역 점프 마르코프 연쇄 몬테 ^[7]카를로의 후방 분포 근사치로 추정할 수 있다.

대체 어프로치

대안적 접근법에는 기대 ^[8]전파가 포함된다.

최근의 연구는 다수의 문서에서 방대한 수의 주제를 포착하는 것을 지원하기 위해 잠재된 디리클레 할당의 추론을 가속화하는 데 초점을 맞추고 있다.앞에서 언급한 접힌 깁스 샘플러의 업데이트 방정식은 그 안에 이용할 수 있는 자연스러운 희소성을 가지고 있다.직관적으로 각 문서에는 ${\displaystyle {토픽K}_{}}$ d$$\ $display style$ K _ { $d$ 의 서브셋만이 포함되어 있고, ${\displaystyle {토픽K}_{}}$ w$$\ $display style$ K _ { $w$ 의 서브셋에만 단어가 표시되므로 위의 업데이트 방정식은 이 희소성을 ^[9]활용하기 위해 다시 작성할 수 있습니다.

${\displaystyle p(Z_{d,n}=k}\propto {C_{k}^{\neg n}+V\beta}}+{\frac {C_{k}^{d}\beta }{C_{k}^{\neg}+Beta }\frac {C}$

이 방정식에서는 세 개의 항이 있는데, 그 중 두 개는 희박하고 다른 하나는 작습니다.이$$ $용어들$을${\displaystyle \mathrm{각각}}$ a, b$,$ $b,$ $c$, $display style$c라고 부릅니다.모든 토픽을 요약하여 각 용어를 정규화하면 다음과 같은 결과가 나옵니다.

${\displaystyle A=\sum _{k=1}^{K}{C_{k}^{\neg n}+V\beta }}$

${\displaystyle B=\sum _{k=1}^{K}{\frac {C_{k}^{d}\beta}{C_{k}^{\neg n}+V\beta }}}$

${\displaystyle C=\sum _{k=1}^{K}{\frac {C_{k}^{w}(\alpha +C_{k}^{d}){C_{k}^{\neg n}+V\beta }}}$

여기서 B$(style$ B$)$는 $문서{\displaystyle }$ d$(style$ d$)$에 기재된 토픽의 합계이며, $(style$ C$)$도 단어 w$(style$ w$)$가 $말뭉치{\displaystyle }$ 전체에 걸쳐 할당되어 있는 토픽의 희박한 $합계임$을 알 수 있습니다.$A는$밀도가$$ 높지만 α$(디스플레이$ 스타일 \alpha$)$와$$β($디스플레이$스타일 \$beta$의 값이 작기 때문에 다른 두 항에 비해 값이 매우 작습니다.

토픽을 샘플링 할 때 랜덤 변수를 s${\displaystyle }$~${\displaystyle U}$ ( ${\displaystyle sa}$A +${\displaystyle B}$ +${\displaystyle C}$ )$$\ $displaystyle$s \ $sim$U ($s$ \ $mid$A +$B$ + $C$)에서 균일하게 샘플링하면 샘플이 어느 버킷에 도착하는지 확인할 수 있습니다.$A는$$$작기 $때문$에 이 버킷에 빠질 가능성은 거의 없습니다.단, 이 버킷에 빠졌을 경우 토픽을 샘플링하는 데 O$(K) 시간$이 $걸립니다$(원래 Collapse Gibbs Sampler와 동일).그러나 다른 두 버킷에 속할 경우 희박한 주제를 기록하면 일부 항목만 확인할 수 있습니다.토픽은 O${\displaystyle (K_{}}$ d$)$ $시간$에 $B{\displaystyle }$$(\$$displaystyle$B$)$ 버킷에서$$ 샘플링할 수 있으며, 토픽은 O$K$ w$)$ $시간$에 C$(\displaystyle$ C$)$ $버킷$에서 샘플링할 수 있습니다. ${\displaystyle {여기}_{}}$서 K$displaystyle$ O$(K_{w}$ 시간에는$$ $K_displaystyle$ K_${$$d$$}$ 시간 및 $K\_d{\displaystyle {}_{}}$$}$입니다.현재 문서와 현재 단어 유형에 각각 할당된 항목의 mber.

각 항목을 샘플링한 후 이러한 버킷을 업데이트하는 작업은 모두 $기본{\displaystyle }$O($)$ {$displaystyle$O($1)}$ 산술$$ 연산입니다.

컴퓨터 상세 측면

다음은 접힌 Gibbs 샘플링 방정식의 도출입니다. $즉{\displaystyle }$, {\$$\ $displaystyle$\ $varphi }$ 및 ${\$ \ $displaystyle \theta }$가 적분됨을 의미합니다.간단히 말하면, 이 파생 자료에서는 모든 문서의 $길이$가 N$(\$인 것으로 가정합니다. 문서의 길이가 다른 경우에도 파생 자료는 동일하게 유효합니다.

모형에 따르면 모형의 총 확률은 다음과 같습니다.

$\displaystyle P({\boldsymbol {W}), {\boldsymbol {Z}, {\boldsymbol {theta }}, {\boldsymbol {varphi }}, {\alpha},\balpha} =\boldsymbol _{K} P(\varphi_{i})_{i_{i}_{{{{i},\}_{{{{{\},\})_J}_{{{{{{P(W_{j,t}\mid \varphi _{Z_{j,t}}),}$

여기서 굵은 글씨로 표시된 변수는 변수의 벡터 버전을 나타냅니다.$먼저{\displaystyle \mathit{}}$, ${\(\$})과$display$(\displaystyle\$boldsymbol\theta })$를 통합해야 합니다.

${\displaystyle{\begin{정렬}&.P({\boldsymbol{Z}},{\boldsymbol{W}};\alpha ,\beta)=\int _{\boldsymbol{\theta}}\int _{\boldsymbol{\varphi}}P({\boldsymbol{W}},{\boldsymbol{Z}},{\boldsymbol{\theta}},{\boldsymbol{\varphi}};\alpha ,\beta)\,d{\boldsymbol{\varphi}}\,d{\boldsymbol{\theta}}\\={}&, \int _{\boldsymbol{\varphi}}\prod{_{i=1}^.K}P(\varphi _{i};\boldsy)\prod _{t=1}^{N}P(W_{j,t}\mid \varphi _{Z_{j,t}),d{boldsymbol {varphi }\int}\boldsymboltambolt}\end { aligned}}$

$모든{\displaystyle }$\$displaystyle$$$$\$는 $서로{\displaystyle }$ 독립적이며 모든 \$displaystyle$ \$varphi에$ 동일합니다$.$따라서 $(\displaystyle\theta)$과 $(\displaystyle\varphi)$을 개별적으로$$ 취급할 수 있습니다.$이제{\displaystyle }$ ${\(\display$ \$theta)$ 부분에만$$ 초점을 맞춥니다.

${\displaystyle \int _{\boldsymbol {\theta } {{M}P(\theta _{j};\alpha)\cisco _{t=1}{N}P(Z_{j,t}\mid \theta _{j}), displaystymboldsymbol {ta ={ta }{mbol {ta =}{m}{mbalphon}{m}{m}{m}{m}{m}{m}{m}{M}{m}$

다음과 같이 $(\displaystyle\theta)$에만 초점을 맞출 수 있습니다.

$\displaystyle \int _{\theta _{j}P(\theta _{j};\alpha)\cisco _{t=1}^{N}P(Z_{j,t}\mid \theta _{j}),d\theta _{j}.}$

사실 j ${\displaystyle t^{}}$(\$displaystyle j^{th$}) $문서$의 모델 숨겨진 부분입니다.이제 위의 방정식의 확률을 진정한 분포식으로 대체하여 명시적 방정식을 작성합니다.

$\displaystyle \int _{\theta _{j}P(\theta _{j};\alpha)\frc _{t=1}^{N}P(Z_{j,t}\mid \theta _{j}),d\int _{j}={\int _{\sum}\frac \theta _{{summa _1}_{sum}_i}}$

${\displaystyle n_{}^{}}$ j${\displaystyle {,}_{}^{}}$ ${\displaystyle {}_{}^{}}$ i$${\$displaystyle n_{j,r}^{i}$는 $j{\displaystyle {}^{}}$ ${\displaystyle t^{}}$h $문서$ 내의 단어 토큰의 수이며, 같은 단어 기호(어휘의 $r{\displaystyle {}^{}}$ ${\displaystyle t^{}}$h {$displaystyle$ r$^{th})$는 $i{\displaystyle {}^{}}$ ${\displaystyle t^{}}$h {$displaystyle$ i$^{th}}}$ 토픽에 할당됩니다.${\displaystyle {따라서}_{}^{}}$ n j${\displaystyle {,}_{}^{}}$ ${\displaystyle r_{}^{}}$ ${\displaystyle {}_{}^{}}$는$$3차원 n_{j_{$j,r}^{i}$는 3차원입니다.3차원 중 어느 것이 특정 값으로 제한되지 않는 경우 괄호 안에 있는 점$({\displaystyle }$ ${\displaystyle )}$)(\$displaystyle (\cdot$))을$$ 사용하여 나타냅니다.예를 들어 n${\displaystyle j_{}^{}}$ , (${\displaystyle {)}_{}^{}}$ )$$ \ $displaystyle n_{j,$ ( $cdot$)^{$i}$는 ${\displaystyle i^{}}$\$displaystyle$ i$^{th}$ 토픽에 $할당된j{\displaystyle {}^{}}$ ${\displaystyle {\mathrm{th}}^{}}$ ${\displaystyle {문서}^{}}$내의 $단어$ 토큰의 수를 나타냅니다.따라서 위의 방정식의 오른쪽 부분은 다음과 같이 고쳐 쓸 수 있습니다.

$\displaystyle _{t=1}^{N}P(Z_{j,t}\mid \theta _{j}=\display_{i=1}^{K}\theta _{j,i}^{i}}}.}$

따라서 ${\displaystyle j_{}}$j \$displaystyle \theta$ _${j}$ 통합식을$$ 다음과 같이 변경할 수 있습니다.

$\displaystyle \int _{j}{\frac {Gamma \left(\sum _{i=1}^{K}\alpha _{i}\gamma (\alpha _{i}}}}{i=1}^{K}\ta _{ji}_{i}}{\frac {gampa }_{i}}\param _{i=1}^{K}\theta _{j,i}^{n_{j,\cdot}^{i}+\alpha _{i}-1},d\theta _{j}.}$

적분 내부의 방정식은 디리클레 분포와 동일한 형태를 가집니다.디리클레 분포에 따르면

$({displaystyle \int _{j}{\frac {Gamma \left(\sum _{i=1}^{K_{j,\cdot})}{i}+\alpha _{i}\right}{\gamma (n_{j,\cdot})_i})}$

따라서,

${\displaystyle{\begin{정렬}&, \int _{\theta_{j}}P(\theta_{j};\alpha)\prod _ᆰ^ᆱP(Z_{j,t}\mid \theta_{j})\,d\theta _{j}=\int _{\theta_{j}}{\frac{\Gamma)}{\prod_{i=1}^{K}\Gamma(\alpha_{나는})}}\prod _{i=1}^{K}\theta _{j,i}^{n_{j,(\cdot)}^{나는}+\alpha _{나는}-1}\,d\theta _ᆽ\\[8pt]={}&,{\frac{\G.amma \left(\sum _{i=1}^{K}\alpha _{i}\right)}{{i=1}^{K}\Gamma(\alpha _{i})}{\frac {{i=1}^{K}\Gamma({j,\cdot}^i}\alpha_{i})\gama}a _{i}}}}\frac _{i=1}^{K}\theta _{j,\cdot}^{i}+\alpha _{i}-1}, d\theta _{j}\[8pt]={}&{Gamma \left(\sum _i=1}^{i}_alpha}_{i}_{i}_{i}_{i}_{i}_cdpa}_{i}_{i}_cdfrcdta}_{i}}_i}_{i}\end { aligned}}$

$이제{\displaystyle \mathit{}}$ ${\(*$style$\display\boldsymbol\varphi})$ 파트로$$ 시선을 돌립니다.실제로 $(\$ 파트의$$ 파생은 ${\(\$ $파트$와 매우 유사합니다.여기서는 파생 단계만 나열합니다.

${\displaystyle{\begin{정렬}&, \int _{\boldsymbol{\varphi}}\prod _ᆯ^ᆰP(\varphi_{나는};\beta)\prod _{j=1}^{M}\prod _ᆳ^ᆴP(W_{j,t}\mid \varphi_{Z_{j,t}})\,d{\boldsymbol{\varphi}}\\[8pt]={}&, \prod _{i=1}^{K}\int _{\varphi_{나는}}P(\varphi_{나는};\beta)\prod _ᆼ^ᆽP(W_{j,t}\mid \varphi_{Z_{j,t}})\,d\varphi _{나는}\ _{j=1}^{M}\prod.\[8pt]={}&\prod _{i=1}^{K}\int _{\varphi_{나는}}{\frac{\Gamma)}{\prod_{r=1}^{V}\Gamma(\beta_{r})}}\prod _{r=1}^{V}\varphi _{i,r}^{\beta_{r}-1}\prod _{r=1}^{V}\varphi _{i,r}^{n_{(\cdot),r}^{나는}}\,d\varphi _ᆼ\\[8pt]={}&, \prod _{i=1}^{K}\int _{\varphi_{나는}}{\frac{\Gamma)}.{\prod_{r=1}^{V}\Gamma(\beta_{r})}}\prod _{r=1}^{V}\varphi _{i,r}^{n_{(\cdot),r}^{나는}+\beta _{r}-1}\,d\varphi _ᆷ\\[8pt]={}&, \prod _{i=1}^{K}{\frac{\Gamma)}{\prod_{r=1}^{V}\Gamma(\beta_{r})}}{\frac{\prod_{r=1}^{V}\Gamma(n_{(\cdot),r}^{나는}+\beta _{r})}{\Gamma \left(\sum_{r=1}^{V}n_{(\cdot),r}^{나는}+\beta다.{r}\오른쪽)}}}.\end { aligned}}$

알기 쉽게 하기 위해 $다음$과 같은 최종 방정식을 ${\\$와 ${\\$ 모두$$ $적습니다{\displaystyle \mathit{}}$.

$\displaystyle P({\boldsymbol {Z}), {\boldsymbol {W};\alpha,\alpha}=\display_{j=1}^{M}{\frac {Gamma \left(\sum_i=1}^{K}\right){\gampa_{i}{i=K}{\K}{\K}{\K}{\K}{\}{\ma}Ambalpha}A}left(\sum _{r=1}^{V}\beta _{r}\오른쪽){\beta _{r=1}^{V}\Gamma (\frac _{r=1}^{V}\Gamma (n_{(\cdotr}^{i}+\r}\gama \ma \{{{r})})\gama \ma\{{{{{\}}}}}$

Gibbs 샘플링의 목표는 P${\displaystyle }$( ${\displaystyle Z\mathit{}w\mathit{}}$W ;${\displaystyle \alpha }$ ,${\displaystyle }$β$$) { $displaystyle$ P ( { \ $bold$ symbol {$Z$} } } \ $mid$ { \ $bold symbol${ W} ; \ alpha , \ $beta$} }$$。$이래{\displaystyle }$P (${\displaystyle W\mathit{}}$ ;${\displaystyle \alpha }$ ,$β$ ) \ $displaystyle$ P ( \ $symbold symbol$ { \ symbol { \ symbalphol { \ symbalphol } ) } } } ） } $β)$ $({\boldsymbol {Z},$ {\$boldsymbol {W}};\alpha,\beta})$ 직접$$${\displaystyle .}$요점은 다음과 같은 조건부 확률을 도출하는 것이다.

${\displaystyle P(Z_{(m,n)}\mid {boldsymbol {Z_{-(m,n)}}}, {\boldsymbol {W}}, {\alpha,\boldsymbol {P(Z_{(m,n}), {\boldsymbol}}}}}}, {\boldsymbol}}}}}, {Boldsymbol}}}, {Bol}}, {Bolflack}}, {Bold},$

where ${\displaystyle Z_{(m,n)}}$ denotes the ${\displaystyle Z}$ hidden variable of the ${\displaystyle n^{th}}$ word token in the ${\displaystyle m^{th}}$ document.또한 그 단어의 기호는 어휘 내의 ${\displaystyle v^{}}$ t $(\$ v$^{th$$})$ 단어라고 가정합니다.${\displaystyle {\mathit{Z}}_{\mathbf{}}}$-${\displaystyle {\mathbf{}}_{}}$(${\displaystyle {\mathbf{}\mathit{m}}_{}}$ ,${\displaystyle {\mathbf{}}_{}}$n$$) { $display style$ {$Z$$\_$$${ - ( m , n )$$} } $}$${\displaystyle {}_{}}denotes$ , ${\displaystyle Z_{}}$ (${\displaystyle {}_{}}$m$$, n )$$。 Gibbs ${\displaystyle {\mathrm{샘플링}}_{}}$은 ${\displaystyle Z_{}}$$($${\displaystyle {}_{}}$m , $n$)$a$ a a a for for for for for for for for for for for for for for for （ m , ${\displaystyle {\mathit{n}}_{}}$ )$$。

${\displaystyle P\left(Z_{m,n}\mid {Z_{-(m,n)}}}}, {\boldsymbol {W}};\alpha,\beta \right}}$

${\displaystyle {\mathrm{그러나}}_{}}$Z (${\displaystyle {}_{}}$m ,${\displaystyle n_{}}$) { $displaystyle$Z _ { ($m$ ,$n$ ) } } $can$ 。따라서 위의 방정식은 다음과 같이 단순화할 수 있습니다.

${\displaystyle {begin{(m,n)}P(&Z_{(m,n)}=v\mid {boldsymbol {Z_{-(m,n)}}}}, {\boldsymbol {W};\alpha},\propto P(Z_{m,n})={boldsym}}, {boldsym}}}}{M}\prod _{j\neq m}{\frac {i=1}^{K}\Gamma \left(n_{j,\cdot})^{i}+\alpha _{i}\right}{\Gamma \left(\sum _i=1}^{K}n_{j,\cdot}^{i}_i}_i}_{{{{\}_i}{{{{{\})}_i}{\gamma}{\gma}_}{{{{{{{t){\frac {{i=1}^{K}\Gamma \left(n_{m,\cdot)}^{i}+\alpha_{i}\right}{\Gamma \left(\sum _i=1}^{K}n_{m,\cdot}^i+alpha_{i}\right}_{{i}}_}_}_i}_}_}{{\}}}}}}}}{gamm}}}}}{gamm}}}}}}}}}}}}\\[8pt]&\propto {frac _{i=1}^{K}\Gamma \left (n_{m,\cdot)}^{i}+\alpha _{i}\right}{\Gamma \left (\sum _i=1}^{K_{m,\cdot}^{i}_i}_i}_i}_i}_i}_i}_n_i}_i}_i}_i_i}_i_i_{\i}_i}_i}_i}}}\\[8pt]&\propto \cdot _{i=1}^{K}\Gamma \left(n_{m,\cdot})^{i}+\alpha _{i}\right}\frac {Gamma \left(n_{\cdot}^{K}\i}_i}_{i}\fright}_v}_v}_{i}_{i}\fright}_bright}_{i}_{i}\fright}_{i}_{i}\end { aligned}}$

마지막으로 n ${\displaystyle {j,}_{}^{}}$ ${\displaystyle r_{}^{}}$ ${\displaystyle {,}_{}^{}}$- (${\displaystyle m_{}^{}}$ ,${\displaystyle n_{}^{}}$) { $displaystyle$ $n$_ {$j$ , $r$}^$i$, - ($m$ ,$$${\displaystyle n_{}}$) } $as$ ${\displaystyle {as}_{}^{}}$ 、 n${\displaystyle {}_{}^{}}$j , ${\displaystyle {}_{}^{}}$ $style$ $n$_ {$j$ , $r$}^{$$i } $as$$$ as $as{\displaystyle {}_{}}$ as 、${\displaystyle {}_{}}$Z $_$ { $（ m$, $n$ 。위의 방정식은 감마 함수의 특성을 이용하여 더욱 단순화할 수 있다.먼저 합계를 분할한 후 다시 합계를 병합하여$$k\$displaystyle$k-독립$$ $합계$를 구합니다. 이 합계는 폐기될 수 있습니다.

${\displaystyle{\begin{정렬}&,\propto \prod _{ki\neq}\Gamma \left(n_{m,(\cdot)}^{i,-(m,n)}+\alpha _{나는}\right)\prod _{ki\neq}{\frac{\Gamma)}^{i,-(m,n)}+\beta _{v}\right)}{\Gamma \left(\sum_{r=1}^{V}n_{(\cdot),r}^{i,-(m,n)}+\beta _{r}\right)}}\Gamma \left(n_{m,(\cdot)}^{k,-(m,n)}+\alpha _{k}+1\right){\frac{\Gamma \lef.t(n_{(\cdot),v}^{k,-(m,n)}+\gamma_left(\sum_r=1}^{V}n_{(\cdot),r}^{k,-(m,n)}+\gamma_{r}+1\right)}}\\[8pt]&, =\prod _{ki\neq}\Gamma \left(n_{m,(\cdot)}^{i,-(m,n)}+\alpha _{나는}\right)\prod _{ki\neq}{\frac{\Gamma)}^{i,-(m,n)}+\beta _{v}\right)}{\Gamma \left(\sum_{r=1}^{V}n_{(\cdot),r}^{i,-(m,n)}+\beta _{r}\right)}}\Gamma \left(n_{m,(\cdot)}^{k,-(m,n)}+\alpha _{k}\right){\frac{\Gamma)}^{k,-(m,n)}+\be.있을 거_{v}\right)}{\Gamma \left(\sum_{r=1}^{V}n_{(\cdot),r}^{k,-(m,n)}+\beta _{r}\right)}}\left(n_{m,(\cdot)}^{k,-(m,n)}+\alpha _{k}\right){\frac{n_{(\cdot),v}^{k,-(m,n)}+\beta _{v}}{\sum_{r=1}^{V}n_{(\cdot),r}^{k,-(m,n)}+\beta _{r}}}\\[8pt]&, =\prod _{나는}\Gamma \left(n_{m,(\cdot)}^{i,-(m,n)}+\alpha _{나는}\right)\prod _{나는}{\frac{\Gamma \left(n_{(cm이다.cdot),v}^{i,-(m,n)}+\beta _{v}\right)}{\Gamma \left(\sum_{r=1}^{V}n_{(\cdot),r}^{i,-(m,n)}+\beta _{r}\right)}}\left(n_{m,(\cdot)}^{k,-(m,n)}+\alpha _{k}\right){\frac{n_{(\cdot),v}^{k,-(m,n)}+\beta _{v}}{\sum_{r=1}^{V}n_{(\cdot),r}^{k,-(m,n)}+\beta _{r}}}\\[8pt]&, \propto \left(n_{m,(\cdot)}^{k,-(m,n)}+\alpha _{k}\right){\frac{n_{(\cdot),v}^.{k,-(m,n)}+\sum _{v}}{\sum _{r=1}^{V}n_{(\cdot ,r}^{k,-(m,n)}+\sum _{r}}\end{aligned}}}}}$

Note that the same formula is derived in the article on the Dirichlet-multinomial distribution, as part of a more general discussion of integrating Dirichlet distribution priors out of a Bayesian network.

Related problems

Related models

Topic modeling is a classic solution to the problem of information retrieval using linked data and semantic web technology.^[10] Related models and techniques are, among others, latent semantic indexing, independent component analysis, probabilistic latent semantic indexing, non-negative matrix factorization, and Gamma-Poisson distribution.

The LDA model is highly modular and can therefore be easily extended. The main field of interest is modeling relations between topics. This is achieved by using another distribution on the simplex instead of the Dirichlet. The Correlated Topic Model^[11] follows this approach, inducing a correlation structure between topics by using the logistic normal distribution instead of the Dirichlet. Another extension is the hierarchical LDA (hLDA),^[12] where topics are joined together in a hierarchy by using the nested Chinese restaurant process, whose structure is learnt from data. LDA can also be extended to a corpus in which a document includes two types of information (e.g., words and names), as in the LDA-dual model.^[13] Nonparametric extensions of LDA include the hierarchical Dirichlet process mixture model, which allows the number of topics to be unbounded and learnt from data.

As noted earlier, pLSA is similar to LDA. The LDA model is essentially the Bayesian version of pLSA model. The Bayesian formulation tends to perform better on small datasets because Bayesian methods can avoid overfitting the data. For very large datasets, the results of the two models tend to converge. One difference is that pLSA uses a variable ${\displaystyle d}$ to represent a document in the training set. So in pLSA, when presented with a document the model has not seen before, we fix ${\displaystyle \Pr(w\mid z)}$—the probability of words under topics—to be that learned from the training set and use the same EM algorithm to infer ${\displaystyle \Pr(z\mid d)}$—the topic distribution under ${\displaystyle d}$. Blei argues that this step is cheating because you are essentially refitting the model to the new data.

Spatial models

In evolutionary biology, it is often natural to assume that the geographic locations of the individuals observed bring some information about their ancestry. This is the rational of various models for geo-referenced genetic data.^[7][14]

Variations on LDA have been used to automatically put natural images into categories, such as "bedroom" or "forest", by treating an image as a document, and small patches of the image as words;^[15] one of the variations is called spatial latent Dirichlet allocation.^[16]

See also

• Variational Bayesian methods
• Pachinko allocation
• tf-idf
• Infer.NET

References

External links

This article's use of external links may not follow Wikipedia's policies or guidelines. Please improve this article by removing excessive or inappropriate external links, and converting useful links where appropriate into footnote references. (June 2016) (Learn how and when to remove this template message)

• jLDADMM A Java package for topic modeling on normal or short texts. jLDADMM includes implementations of the LDA topic model and the one-topic-per-document Dirichlet Multinomial Mixture model. jLDADMM also provides an implementation for document clustering evaluation to compare topic models.
• STTM A Java package for short text topic modeling (https://github.com/qiang2100/STTM). STTM includes these following algorithms: Dirichlet Multinomial Mixture (DMM) in conference KDD2014, Biterm Topic Model (BTM) in journal TKDE2016, Word Network Topic Model (WNTM ) in journal KAIS2018, Pseudo-Document-Based Topic Model (PTM) in conference KDD2016, Self-Aggregation-Based Topic Model (SATM) in conference IJCAI2015, (ETM) in conference PAKDD2017, Generalized P´olya Urn (GPU) based Dirichlet Multinomial Mixturemodel (GPU-DMM) in conference SIGIR2016, Generalized P´olya Urn (GPU) based Poisson-based Dirichlet Multinomial Mixturemodel (GPU-PDMM) in journal TIS2017 and Latent Feature Model with DMM (LF-DMM) in journal TACL2015. STTM also includes six short text corpus for evaluation. STTM presents three aspects about how to evaluate the performance of the algorithms (i.e., topic coherence, clustering, and classification).
• Lecture that covers some of the notation in this article: LDA and Topic Modelling Video Lecture by David Blei or same lecture on YouTube
• D. Mimno's LDA Bibliography An exhaustive list of LDA-related resources (incl. papers and some implementations)
• Gensim, a Python+NumPy implementation of online LDA for inputs larger than the available RAM.
• topicmodels and lda are two R packages for LDA analysis.
• MALLET Open source Java-based package from the University of Massachusetts-Amherst for topic modeling with LDA, also has an independently developed GUI, the Topic Modeling Tool
• LDA in Mahout implementation of LDA using MapReduce on the Hadoop platform
• Latent Dirichlet Allocation (LDA) Tutorial for the Infer.NET Machine Computing Framework Microsoft Research C# Machine Learning Framework
• LDA in Spark: Since version 1.3.0, Apache Spark also features an implementation of LDA
• LDA, exampleLDA MATLAB implementation