분자역학

Molecular mechanics
힘장은 이 에탄 분자의 결합 신장 에너지를 최소화하기 위해 사용된다.

분자역학은 고전역학을 이용하여 분자계를 모형화한다.Born-Oppenheimer 근사치는 유효하다고 가정하고 모든 시스템의 잠재적 에너지는 힘장을 사용하는 핵 좌표의 함수로 계산한다.분자역학은 크기가 작은 것부터 큰 것까지 다양한 분자 시스템이나 수천에서 수백만 개의 원자를 가진 물질 집합체를 연구하는데 사용될 수 있다.

전원자 분자역학 방법에는 다음과 같은 특성이 있습니다.

  • 각 원자는 하나의 입자로 시뮬레이션됩니다.
  • 각 입자는 반지름(일반적으로 반데르발스 반지름), 편광성 및 일정한 순 전하(일반적으로 양자 계산 및/또는 실험에서 도출됨)가 할당됩니다.
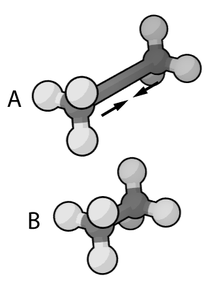
  • 결합 상호작용은 실험 또는 계산된 결합 길이와 동일한 평형 거리를 갖는 스프링으로 처리된다.

이 테마에 대한 변형도 가능합니다.예를 들어, 많은 시뮬레이션은 각 말단 메틸기 또는 중간 메틸렌 단위를 하나의 입자로 간주하는 통합 원자 표현을 사용해 왔으며, 대규모 단백질 시스템은 일반적으로 아미노산 당 2-4개의 입자를 할당하는 비즈 모델을 사용하여 시뮬레이션된다.

기능적 형태

분자역학 퍼텐셜 에너지는 연속체 용매와 함께 기능한다.

화학에서 원자간 전위함수 또는 힘장이라고 불리는 다음의 기능 추상화는 개별 에너지 용어의 합으로 주어진 구조에서 분자 시스템의 전위 에너지(E)를 계산합니다.

여기서 공유 및 비공유 기여의 구성요소는 다음과 같은 합계로 주어진다.

전위함수 또는 힘장의 정확한 기능 형태는 사용되는 특정 시뮬레이션 프로그램에 따라 달라집니다.일반적으로 결합항과 각도항은 가우스 등의 ab-initio형 계산을 하는 소프트웨어로 실행된 전자구조의 실험 또는 이론 계산에서 도출된 평형 결합 길이 값을 중심으로 한 고조파 전위로 모델링된다.진동 스펙트럼의 정확한 재생을 위해 계산 비용을 들여 모스 전위를 대신 사용할 수 있다.이면체 항 또는 비틀림 항은 일반적으로 여러 개의 최소값을 가지며, 따라서 구현에 따라 특정 기능 형태가 달라지지만 고조파 발진기로 모델링할 수 없습니다.이 등급의 용어에는 부적절한 이면체 항이 포함될 수 있으며, 이면체 항은 면외 편차에 대한 보정 계수로 기능합니다(예를 들어 벤젠 고리를 평면으로 유지하거나 연합 원자 표현에서 사면체 원자의 기하학적 구조와 키랄리티를 수정하는 데 사용할 수 있습니다).

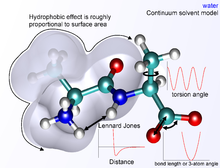
비결합 항은 전형적인 원자가 그 이웃의 몇 개에만 결합되어 있지만 분자의 다른 모든 원자와 상호작용하기 때문에 전체적으로 계산하기 위해 훨씬 더 많은 계산 비용이 든다.다행히도 판데르발스라는 용어는 빠르게 감소한다.일반적으로 6-12 레너드-존스 전위를 사용하여 모델링된다. 즉, 유인력은 r, 반발력은 r로−12 떨어져 나간다−6. 여기서 r은 두 원자 사이의 거리를 나타낸다.그러나 반발력은−12 기하급수적으로 증가하므로 반발 부품 r은 비물리적입니다.Lennard-Jones 6–12의 잠재력에 의한 반데르발스 힘 설명은 부정확성을 초래하며,[1] 이는 단거리에서 중요해진다.일반적으로 컷오프 반경은 컷오프보다 거리가 큰 원자쌍이 0의 반데르발스 상호작용 에너지를 갖도록 계산을 고속화하기 위해 사용된다.

정전기 항은 거리에 따라 빠르게 떨어지지 않기 때문에 잘 계산하기 어렵기로 악명 높으며, 장거리 정전기 상호작용은 종종 연구 대상 시스템(특히 단백질의 경우)의 중요한 특징이다.기본적인 기능 형태는 쿨롱 전위이며, 이는 r로만−1 떨어집니다.이 문제에 대처하기 위해서는 다양한 방법이 사용되며, 가장 간단한 방법은 van der Waals 용어에 사용되는 것과 유사한 컷오프 반지름입니다.그러나, 이것은 내부에 있는 원자와 반지름 바깥의 원자 사이에 급격한 불연속성을 초래한다.외관 정전기 에너지를 변조하는 스위칭 또는 스케일링 함수는 외부 및 내부 컷오프 반지름에서 0에서 1까지 매끄럽게 변화하는 스케일링 계수를 계산한 에너지를 곱하는 보다 정확한 방법입니다.그 밖에도 복잡하지만 계산 부하가 높은 방법으로는 파티클 메쉬 Ewald(PME)와 멀티폴 알고리즘이 있습니다.

각 에너지 항의 함수 형태 외에, 유용한 에너지 함수는 힘 상수, 판데르발스 승수 및 기타 상수 항에 대한 매개변수를 할당해야 한다.이러한 용어는 평형 결합, 각도 및 이면체 값, 부분 전하 값, 원자 질량과 반지름, 에너지 함수 정의와 함께 총칭하여 힘장이라고 한다.파라미터화는 일반적으로 실험값 및 이론적 계산결과와의 합치를 통해 이루어집니다.노먼 L. 마지막 MM4 버전에서 Allinger의 힘 장은 0.35 kcal/mol의 RMS 오차를 가진 탄화수소 발열, 24 cm의−1 RMS 오차를 가진 진동 스펙트럼, 2.2°의 회전 장벽, 0.004Ω 이내의 C-C 결합 길이 및 1°[2] 이내의 C-C-C 각도에 대해 계산한다.이후의 MM4 버전은 지방족 [3]아민과 같은 헤테로아톰을 가진 화합물도 포함한다.

각 힘 필드는 내부적으로 일치하도록 매개변수가 지정되지만, 일반적으로 한 힘장에서 다른 힘장으로 매개 변수를 전송할 수 없습니다.

응용 분야

분자역학의 주된 용도는 분자역학 분야이다.이것은 힘 필드를 사용하여 각 입자에 작용하는 힘을 계산하고 입자의 역학을 모델링하고 궤적을 예측하는 데 적합한 적분자를 사용합니다.충분한 샘플링이 주어지고 에르고드 가설에 따라 분자역학 궤적은 시스템의 열역학 파라미터를 추정하거나 반응속도 및 메커니즘과 같은 운동학적 특성을 탐사하는데 사용될 수 있다.

분자역학의 또 다른 적용은 에너지 최소화이며, 여기서 힘의 장은 최적화 기준으로 사용됩니다.이 방법은 국소 에너지 최소의 분자 구조를 찾기 위해 적절한 알고리즘(예: 가장 가파른 하강)을 사용한다.이러한 최소값은 분자의 안정적인 컨포머(선택된 힘장)에 해당하며 분자 운동은 이러한 안정적인 컨포머 간의 진동 및 상호 변환으로 모델링될 수 있다.따라서 글로벌 에너지 최소값(및 기타 낮은 에너지 상태)을 찾기 위해 글로벌 에너지 최적화와 결합된 로컬 에너지 최소화 방법을 찾는 것이 일반적입니다.한정된 온도에서 분자는 대부분의 시간을 이러한 낮은 상태의 분자 성질을 지배합니다.글로벌 최적화는 시뮬레이션 어닐링, 메트로폴리스 알고리즘 및 기타 몬테카를로 방법을 사용하거나 이산 또는 연속 최적화의 다른 결정론적 방법을 사용하여 달성할 수 있다.힘 장은 자유 에너지의 엔탈피 성분만을 나타내지만(그리고 이 성분만 에너지 최소화 중에 포함), 일반 모드 분석과 같은 추가 방법을 사용하여 엔탈로피 성분을 포함할 수 있다.

분자역학 퍼텐셜 에너지 함수는 결합 상수,[4][5][6][7][8] 단백질 접힘 속도론,[9] 양성자 평형,[10] 활성 부위 좌표 [6][11]및 결합 [12]부위의 설계에 사용되어 왔다.

환경과 솔루션

분자역학에서, 관심 있는 분자를 둘러싼 환경을 정의하는 몇 가지 방법이 존재합니다.시스템은 주변 환경이 없는 진공(기상 시뮬레이션)에서 시뮬레이션할 수 있지만, 분자 기하학, 특히 하전 분자에 아티팩트를 도입하기 때문에 일반적으로 바람직하지 않습니다.일반적으로 용제 분자와 상호작용하는 표면 전하가 대신 서로 상호작용하여 다른 환경에서는 존재할 수 없는 분자 형태를 생성합니다.시스템을 용해시키는 가장 정확한 방법은 명시적인 물 분자를 관심 분자와 함께 시뮬레이션 상자에 넣고 물 분자를 다른 분자의 분자와 같이 상호작용하는 입자로 처리하는 것입니다.물을 단순한 단단한 구체(연합 원자 모델), 고정된 결합 각도를 가진 세 개의 개별 입자 또는 산소 원자의 짝을 이루지 않은 전자를 설명하기 위한 네 개 또는 다섯 개의 개별 상호작용 중심으로서 나타내는 복잡성이 증가하는 다양한 물 모델이 존재합니다.물 모델이 복잡해짐에 따라 관련 시뮬레이션은 계산 집약도가 높아집니다.암묵적인 용매화에서 타협 방법이 발견되었는데, 이것은 명시적으로 표현된 물 분자를 물 분자(또는 지질과 같은 다른 용매)의 평균적인 행동을 재현하는 수학식으로 대체한다.이 방법은 진공 시뮬레이션에서 발생하는 아티팩트를 방지하고 벌크 용매 특성을 잘 재현하는데 유용하지만, 각각의 물 분자가 용매 모델에 의해 잘 포착되지 않은 용매와의 특정한 상호작용을 재현할 수 없습니다. 예를 들어, 물 분자는 수소 결합 네트워크의 일부입니다.단백질[13]

소프트웨어 패키지

주요 기사:분자역학 모델링 소프트웨어 비교

이것은 제한된 목록입니다. 더 많은 패키지를 사용할 수 있습니다.

「 」를 참조해 주세요.

레퍼런스

  1. ^ Zgarbova M, et al. (2010). "Large-scale compensation of errors in pairwise-additive empirical force fields: comparison of AMBER intermolecular terms with rigorous DFT-SAPT calculations". Phys. Chem. Chem. Phys. 12 (35): 10476–10493. Bibcode:2010PCCP...1210476Z. doi:10.1039/C002656E. PMID 20603660.
  2. ^ Allinger, N. L., Chen, K., Lii, J.-H. J. Compute. 화학: 1996, 17, 642 https://onlinelibrary.wiley.com/doi/abs/10.1002/%28SICI%291096-987X%28199604%2917%3A5/6%3C642%3A%3AAID-JCC6%3E3.0.CO%3B2-U
  3. ^ 궈샹첸, 젠후이리, 이판, 노먼 L.앨린저 J. 컴퓨터 화학 2007, 28, 2391 https://onlinelibrary.wiley.com/doi/full/10.1002/jcc.20737
  4. ^ Kuhn B, Kollman PA (October 2000). "Binding of a diverse set of ligands to avidin and streptavidin: an accurate quantitative prediction of their relative affinities by a combination of molecular mechanics and continuum solvent models". Journal of Medicinal Chemistry. 43 (20): 3786–91. doi:10.1021/jm000241h. PMID 11020294.
  5. ^ Huo S, Massova I, Kollman PA (January 2002). "Computational alanine scanning of the 1:1 human growth hormone-receptor complex". J Comput Chem. 23 (1): 15–27. doi:10.1002/jcc.1153. PMID 11913381. S2CID 10381457.
  6. ^ a b Mobley DL, Graves AP, Chodera JD, McReynolds AC, Shoichet BK, Dill KA (August 2007). "Predicting absolute ligand binding free energies to a simple model site". J Mol Biol. 371 (4): 1118–34. doi:10.1016/j.jmb.2007.06.002. PMC 2104542. PMID 17599350.
  7. ^ Wang J, Kang X, Kuntz ID, Kollman PA (April 2005). "Hierarchical database screenings for HIV-1 reverse transcriptase using a pharmacophore model, rigid docking, solvation docking, and MM-PB/SA". Journal of Medicinal Chemistry. 48 (7): 2432–44. doi:10.1021/jm049606e. PMID 15801834.
  8. ^ Kollman PA, Massova I, Reyes C, et al. (December 2000). "Calculating structures and free energies of complex molecules: combining molecular mechanics and continuum models". Acc Chem Res. 33 (12): 889–97. CiteSeerX 10.1.1.469.844. doi:10.1021/ar000033j. PMID 11123888.
  9. ^ Snow CD, Nguyen H, Pande VS, Gruebele M (November 2002). "Absolute comparison of simulated and experimental protein-folding dynamics". Nature. 420 (6911): 102–6. Bibcode:2002Natur.420..102S. doi:10.1038/nature01160. PMID 12422224. S2CID 1061159.
  10. ^ Barth P, Alber T, Harbury PB (March 2007). "Accurate, conformation-dependent predictions of solvent effects on protein ionization constants". Proc Natl Acad Sci USA. 104 (12): 4898–903. Bibcode:2007PNAS..104.4898B. doi:10.1073/pnas.0700188104. PMC 1829236. PMID 17360348.
  11. ^ Chakrabarti R, Klibanov AM, Friesner RA (July 2005). "Computational prediction of native protein ligand-binding and enzyme active site sequences". Proc Natl Acad Sci USA. 102 (29): 10153–8. Bibcode:2005PNAS..10210153C. doi:10.1073/pnas.0504023102. PMC 1177389. PMID 15998733.
  12. ^ Boas FE, Harbury PB (July 2008). "Design of Protein-Ligand Binding Based on the Molecular-Mechanics Energy Model". J Mol Biol. 380 (2): 415–24. doi:10.1016/j.jmb.2008.04.001. PMC 2569001. PMID 18514737.
  13. ^ Cramer, Christopher J. (2004). Essentials of computational chemistry : theories and models (2nd ed.). Chichester, West Sussex, England: Wiley. ISBN 0-470-09182-7. OCLC 55887497.
  14. ^ ACEMD - GPU MD
  15. ^ 아스칼라프
  16. ^ 코스모스
  17. ^ StruMM3D(STR3DI32)
  18. ^ Wayback Machine에서 2009-12-16으로 아카이브된 조디악

외부 링크