다중 기준 의사결정 분석

Multiple-criteria decision analysis
"MCDM"은 여기서 리디렉션된다. 우주론에서 사용하는 방법은 메타 콜드 암흑 물질을 참조하십시오.
참고 항목: 다목적 최적화
금융 포트폴리오의 수익 극대화 및 리스크 최소화 시 두 가지 기준 그림(빨간 점의 Pareto 최적점)

다중 기준 의사결정(MCDM) 또는 다중 기준 의사결정 분석(MCDA)은 의사결정(일상생활과 기업, 정부, 의료 등 환경 모두에서)에서 여러 상충되는 기준을 명시적으로 평가하는 운영 연구의 하위 분야다. 옵션 평가에서 상충되는 기준은 전형적으로 비용이나 가격이 일반적으로 주요 기준 중 하나이며, 품질의 일부 측정은 전형적으로 다른 기준이며, 비용과 쉽게 상충된다. 자동차를 구입할 때 비용, 편안함, 안전 및 연비가 우리가 고려하는 주요 기준 중 일부일 수 있다 – 가장 싼 차가 가장 편안하고 안전한 차라는 것은 이례적이다. 포트폴리오 경영에서 경영자들은 높은 수익을 얻는 동시에 위험을 줄이는 데 관심이 있지만 높은 수익을 가져올 잠재력이 있는 주식들은 전형적으로 손해를 볼 위험이 높다. 서비스 산업에서 고객 만족도와 서비스 제공 비용은 근본적으로 상충되는 기준이다.

일상 생활에서 사람들은 대개 여러 가지 기준을 암묵적으로 따지고 있으며, 직관에 의해서만 이루어지는 그러한 결정의 결과에 편안할 수도 있다.[1] 한편, 지분이 높을 때는 문제를 적절히 구조화하고 복수의 기준을 명시적으로 평가하는 것이 중요하다.[2] 원전 건설 여부, 건설 장소 등을 결정함에 있어 다중 기준과 관련된 매우 복잡한 사안이 있을 뿐만 아니라 그 결과에 깊은 영향을 받는 당사자도 다수 존재한다.

복잡한 문제를 잘 구조화하고 여러 기준을 명확하게 고려하는 것은 더 많은 정보에 입각한 더 나은 의사결정으로 이어진다. 1960년대 초 현대 다기준 의사결정 기강이 시작된 이래 이 분야에서 중요한 진보가 있었다. 전문화된 의사결정 소프트웨어에 의해 구현된 많은 다양한 접근법과 방법들이 정치, 사업에서 환경, 에너지까지 다양한 분야에 적용하기 위해 개발되었다.[3][4][5]

기초, 개념, 정의

MCDM 또는 MCDA는 다중 기준 의사결정 및 다중 기준 의사결정 분석을 위한 잘 알려진 두문자어다; 스탠리 시온츠는 기업가적 청중을 대상으로 한 1979년 논문 "MCDM - 로마 숫자가 아니라면, 그렇다면 무엇이냐"로 두문자를 대중화하는데 도움을 주었다.

MCDM은 다중 기준과 관련된 의사결정 및 계획 문제의 구조화 및 해결과 관련이 있다. 이러한 문제에 직면한 의사결정자를 지원하는 것이 목적이다. 일반적으로 이러한 문제에 대한 고유한 최적 솔루션이 존재하지 않으며 솔루션 간 차별화를 위해 의사결정자의 선호도를 사용할 필요가 있다.

"해결"은 다른 방식으로 해석될 수 있다. 그것은 이용 가능한 대안들(여기서 "최상"은 의사결정자의 "가장 선호하는 대안"으로 해석될 수 있는)에서 "최상" 대안을 선택하는 것과 일치할 수 있다. "해결력"에 대한 또 다른 해석은 좋은 대안의 작은 세트를 선택하거나 다른 선호 세트로 대안을 그룹화하는 것일 수 있다. 극단적인 해석은 모든 "효율적" 또는 "연관적" 대안들을 찾는 것일 수 있다(이 대안들은 우리가 곧 정의할 것이다.

문제의 난이도는 둘 이상의 기준이 존재하는 데서 기인한다. 선호 정보를 포함하지 않고 얻을 수 있는 MCDM 문제에 대한 고유한 최적의 해결책은 더 이상 존재하지 않는다. 최적 용액의 개념은 종종 무염 용액 세트로 대체된다. 어떤 기준에서도 다른 기준에서 희생하지 않고 개선할 수 없는 경우, 용액을 무첨가라고 한다. 따라서 의사결정자는 무첨가 세트에서 솔루션을 선택하는 것이 타당하다. 그렇지 않으면, 그녀는 기준의 일부나 전부를 더 잘 할 수 있고, 그것들 중 어떤 것에서도 더 나쁘게 할 수 없을 것이다. 그러나 일반적으로 비염화 솔루션 세트는 너무 커서 최종 선택을 위해 의사결정자에게 제시할 수 없다. 따라서 의사결정자가 선호하는 솔루션(또는 대안)에 집중할 수 있도록 도와주는 도구가 필요하다. 보통 사람은 다른 사람들을 위해 특정한 기준을 "교환"해야 한다.

MCDM은 1970년대부터 활발한 연구 분야였다. 국제 다중 기준 의사결정 협회,[6] MCDA의 유로 워킹 그룹,[7] MCDM의 AIND 섹션 등 MCDM 관련 기관이 여럿 있다.[8] 역사는 쾨살란, 왈레니우스, 시온츠(2011)를 참조한다.[9] MCDM은 다음을 포함한 많은 분야에서 지식을 활용한다.

A유형학

MCDM 문제와 방법에는 서로 다른 분류가 있다. MCDM 문제의 주요 구분은 솔루션이 명시적으로 정의되어 있는지 암묵적으로 정의되어 있는지에 기초한다.

  • 다중 기준 평가 문제: 이러한 문제들은 해결 과정의 초기에 분명히 알려진 한정된 수의 대안들로 구성된다. 각각의 대안은 여러 기준에서 그것의 성과로 표현된다. 이 문제는 의사결정자(DM)를 위한 최선의 대안을 찾거나 일련의 좋은 대안을 찾는 것으로 정의될 수 있다. 또한 대안의 "구분"이나 "분류"에도 관심이 있을 수 있다. 분류란 선호 순서가 정해진 클래스의 집합에 대안을 배치하는 것(예: 국가에 신용 비율 할당)을 말하며, 분류는 비순번 집합에 대안을 배정하는 것(예: 증상에 따라 환자를 진단하는 것)을 말한다. 이 범주의 일부 MCDM 방법은 Triantaphyllou가 2000년 이 주제에 대해 저서에서 비교적으로 연구하였다.[10]
  • 다중 기준 설계 문제(복수의 객관적 수학적 프로그래밍 문제): 이러한 문제들에서는 대안이 명시적으로 알려져 있지 않다. 수학적 모델을 풀면 대안(솔루션)을 찾을 수 있다. 대안의 수는 무한하다(카운트할 수 있건 없건) 또는 유한하지만, 일반적으로 기하급수적으로 크다(유한 도메인에 걸친 변수의 수).

평가 문제든 설계 문제든 솔루션을 구분하기 위해서는 DM의 선호 정보가 필요하다. MCDM 문제에 대한 해결 방법은 일반적으로 DM에서 얻은 선호 정보의 타이밍에 기초하여 분류된다.

프로세스 시작 시 DM의 선호 정보가 필요한 방법이 있어 문제를 본질적으로 단일 기준 문제로 전환한다. 이러한 방법은 "선호도의 사전 표현"에 의해 작동한다고 한다. 가치함수를 추정하거나 "외부 관계"의 개념을 사용한 방법, 분석적 계층화 과정 및 일부 의사결정 규칙 기반 방법들은 선호의 사전 표현을 활용하여 복수의 기준 평가 문제를 해결하려고 한다. 이와 유사하게, 가치함수를 구성하여 선호의 사전 표현 방식을 이용하여 다중 기준 설계 문제를 해결하기 위한 방법이 개발되었다. 아마도 이러한 방법들 중 가장 잘 알려진 것이 목표 프로그래밍일 것이다. 일단 가치함수가 구성되면, 결과적인 단일 객관적 수학적 프로그램이 해결되어 선호되는 해결책을 얻는다.

일부 방법은 솔루션 프로세스 전반에 걸쳐 DM의 선호 정보를 필요로 한다. 이를 "선호의 진보적 표현"이 필요한 대화형 방법 또는 방법이라고 한다. 이러한 방법은 다중 기준 평가(예: Geoffrion, Dyer 및 Feinberg, 1972년,[11] Keoksalan 및 Sagala, 1995년[12] 참조)와 설계 문제(Steuer, 1986년[13] 참조) 모두에 대해 잘 개발되었다.

다중 기준 설계 문제는 일반적으로 암묵적으로 정의된 해결책을 밝히기 위해 일련의 수학 프로그래밍 모델의 해법이 필요하다. 이러한 문제에 대해서는 "효율적인 해결책"의 표현이나 근사치도 관심의 대상이 될 수 있다. 이 범주를 "선호의 사후 표현"이라고 하며, 이는 DM의 관여가 "관심 있는" 해결책의 명시적 폭로 이후 시작됨을 의미한다(예: 카라사칼과 쾨살란, 2009[14] 참조).

수학 프로그래밍 모델이 정수 변수를 포함하면 설계 문제는 풀기 어려워진다. 다목적 결합 최적화(MOCO)는 상당한 계산상의 어려움을 초래하는 그러한 문제의 특별한 범주를 구성한다(검토는 Ehrgott와 Gandibleux, [15]2002년 참조).

표현 및 정의

MCDM 문제는 기준 공간이나 의사결정 공간에 표현될 수 있다. 또는 가중 선형 함수에 의해 서로 다른 기준이 결합되는 경우, 중량 공간에 문제를 나타낼 수도 있다. 다음은 기준과 무게 공간에 대한 시연과 몇 가지 공식적 정의들이다.

기준 공간 표현

몇 가지 기준을 사용하여 특정 문제 상황에서 해결책을 평가한다고 가정해 봅시다. 각 기준에서 더 많은 것이 더 낫다고 가정하자. 그 다음, 가능한 모든 해결책 중에서, 우리는 고려된 모든 기준에서 잘 작동하는 해결책에 이상적으로 관심이 있다. 그러나 모든 고려대상 기준에서 우수한 성능을 발휘하는 단일 솔루션은 없을 것으로 보인다. 일반적으로 어떤 솔루션은 어떤 기준에서 좋은 성능을 발휘하고 어떤 솔루션은 다른 기준에서 좋은 성능을 발휘한다. 기준 간 거래 방법을 찾는 것은 MCDM 문헌의 주요 노력 중 하나이다.

수학적으로 위의 논거에 해당하는 MCDM 문제는 다음과 같이 나타낼 수 있다.

"최대" q
의 대상이 되다
Q ∈ Q

여기서 Q는 k 기준함수의 벡터(객체함수)이며 Q는 실현 가능한 집합인 Q ⊆ R이다k.

Q가 (대안들의 집합에 의해) 명시적으로 정의되는 경우, 결과적인 문제를 다중 기준 평가 문제라고 한다.

Q가 암묵적으로 정의되는 경우(제약조건 집합에 의해) 결과적인 문제를 다중 기준 설계 문제라고 한다.

인용 부호는 벡터의 최대화가 잘 정의된 수학적 연산이 아님을 나타내기 위해 사용된다. 이는 모든 기준에서 좋은 성과를 내는 솔루션이 존재하지 않을 때 기준 간(일반적으로 의사결정자의 선호에 근거) 트레이드오프를 해결할 방법을 찾아야 한다는 주장에 해당한다.

의사결정 공간 표현

결정 공간은 우리가 이용할 수 있는 가능한 결정들의 집합에 해당한다. 기준 값은 우리가 내린 결정의 결과가 될 것이다. 따라서, 우리는 의사결정 공간에서 상응하는 문제를 정의할 수 있다. 예를 들어, 제품을 설계할 때 우리는 제품을 평가하는 성능 측정(기준)에 영향을 미치는 설계 매개변수(결정 변수)를 각각 결정한다.

수학적으로 다중 기준 설계 문제는 다음과 같이 의사결정 공간에 나타낼 수 있다.

여기서 는 실현 가능한 집합이며, n 크기의 의사결정 변수 벡터다.

잘 발달된 특수 사례는 선형 불평등과 평등에 의해 정의된 다면체일 때 얻는다. 모든 객관적 기능이 의사결정 변수에 있어 선형인 경우, 이러한 변화는 MCDM 문제의 중요한 하위 클래스인 다중 객관적 선형 프로그래밍(MOLP)으로 이어진다.

MCDM의 중심에는 몇 가지 정의가 있다. 밀접하게 관련된 두 가지 정의는 비자유도(기준 공간 표현에 기초하여 정의됨)와 효율성(결정 변수 표현에 기초하여 정의됨)이다.

정의 1. q* ∈ Q는 q q*와 q q q*와 같은 q q q q와 같은 q q q q * q q와 같은 q q q q가 존재하지 않는 경우 q q가 무첨가된다.

대략적으로, 고려된 모든 기준에서 사용 가능한 다른 솔루션보다 뒤떨어지지 않는 한, 용액은 무염화된다.

정의 2. x* ∈ X는 f(x) ≥ f(x*) 및 f(x) ≠ f(x*)와 같이 다른 x * X가 존재하지 않는 경우 효율적이다.

MCDM 문제가 의사결정 상황을 잘 나타낸다면 DM에서 가장 선호하는 해결책은 의사결정 공간에서 효율적인 해결책이 되어야 하며, 그 이미지는 기준 공간에서 무첨가점이다. 다음의 정의도 중요하다.

정의 3. q* ∈ Q는 q > q*와 같은 또 다른 q another Q가 존재하지 않는 경우 약하게 무첨가된다.

정의 4. x* ∈ X는 다음과 같은 다른 x ∈ X가 존재하지 않는다면 약하게 효율적이다.

약하게 무첨가된 포인트에는 모든 무첨가 포인트와 일부 특수 지배 포인트가 포함된다. 이러한 특수 우위 포인트의 중요성은 이러한 포인트들이 실무에서 흔히 나타나며, 비포화 포인트와 구별하기 위해 각별한 주의가 필요하다는 사실에서 비롯된다. 예를 들어, 만약 우리가 단일 목표를 최대화한다면, 우리는 약하게 지배되는 무염화 지점이 될 수도 있다. 약하게 무염화 세트의 지배적인 지점은 기준 공간의 수직 평면 또는 수평 평면(하이퍼플레인)에 위치한다.

Ideal point: (in criterion space) represents the best (the maximum for maximization problems and the minimum for minimization problems) of each objective function and typically corresponds to an infeasible solution.

Nadir point: (in criterion space) represents the worst (the minimum for maximization problems and the maximum for minimization problems) of each objective function among the points in the nondominated set and is typically a dominated point.

The ideal point and the nadir point are useful to the DM to get the "feel" of the range of solutions (although it is not straightforward to find the nadir point for design problems having more than two criteria).

Illustrations of the decision and criterion spaces

The following two-variable MOLP problem in the decision variable space will help demonstrate some of the key concepts graphically.

Figure 1. Demonstration of the decision space

In Figure 1, the extreme points "e" and "b" maximize the first and second objectives, respectively. The red boundary between those two extreme points represents the efficient set. It can be seen from the figure that, for any feasible solution outside the efficient set, it is possible to improve both objectives by some points on the efficient set. Conversely, for any point on the efficient set, it is not possible to improve both objectives by moving to any other feasible solution. At these solutions, one has to sacrifice from one of the objectives in order to improve the other objective.

Due to its simplicity, the above problem can be represented in criterion space by replacing the x's with the f 's as follows:

Figure 2. Demonstration of the solutions in the criterion space
Max f1
Max f2
subject to
f1 + 2f2 ≤ 12
2f1 + f2 ≤ 12
f1 + f2 ≤ 7
f1 – f2 ≤ 9
−f1 + f2 ≤ 9
f1 + 2f2 ≥ 0
2f1 + f2 ≥ 0

우리는 기준 공간을 그림 2에 그래픽으로 제시한다. 기준 공간의 비감지점(결정 영역의 효율적인 해결책에 대응)을 보다 쉽게 검출할 수 있다. 실현 가능한 공간의 북동부 지역은 비점화 지점 세트를 구성한다(최대화 문제를 위한).

비염화 솔루션 생성

비염화 솔루션을 생성하는 방법에는 여러 가지가 있다. 우리는 이 중 두 가지를 논의할 것이다. 첫 번째 접근방식은 특별한 종류의 비염화 솔루션을 생성할 수 있는 반면, 두 번째 접근방식은 비염화 솔루션을 생성할 수 있다.

  • 가중 합계(Gass & Saaty, 1955[16])

만약 우리가 각각의 기준을 양의 가중치로 곱하고 가중치를 합산하여 여러 기준을 하나의 기준으로 결합한다면, 결과적인 단일 기준 문제에 대한 해결책은 특별한 효율적 해결책이다. 이러한 특별한 효율적 솔루션은 사용 가능한 솔루션 집합의 구석점에 나타난다. 코너 포인트에 있지 않은 효율적인 솔루션은 특별한 특성을 가지고 있으며 이 방법은 그러한 포인트를 찾을 수 없다. 수학적으로 우리는 이 상황을 다음과 같이 나타낼 수 있다.

max = 0
의 대상이 되다
X X X

가중치를 변화시킴으로써 가중치는 설계 문제에 대한 효율적인 극한점 해결책과 평가 문제에 대한 지원(무포화) 포인트를 생성하는데 사용될 수 있다.

  • 업적 스칼라화 함수(Wierzbicki, 1980[17])
그림 3. 달성 스칼라화 함수를 사용하여 비포밍 세트에 점 투사

성취 스칼라화 기능도 매우 특별한 방법으로 가중치를 부여하여 여러 기준을 하나의 기준으로 결합한다. 이들은 기준점에서 벗어나 이용 가능한 효율적인 솔루션으로 직사각형 등고선을 만든다. 이 특별한 구조는 어떤 효율적인 해결책에도 도달할 수 있도록 성취도를 높이는 기능을 강화한다. 이것은 이러한 기능을 MCDM 문제에 매우 유용하게 만드는 강력한 속성이다.

수학적으로 우리는 다음과 같은 해당 문제를 나타낼 수 있다.

최소 s(g, q, w, ρ) = 최소 {maxi [(gi - qi)/wi ] + ρ σi (gi - qi)},
의 대상이 되다
Q ∈ Q

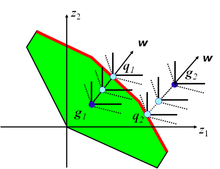
달성 스칼라화 함수는 효율적인 변경에 대한 모든 포인트(실현 가능 또는 실현 불가능)를 투영하는 데 사용할 수 있다. 어떤 지점(지원 여부)에도 도달할 수 있다. 비효율적인 해결책 생성을 피하기 위해 목표함수의 두 번째 항이 필요하다. 그림 3은 달성 스칼라화 함수를 사용하는 방향을 따라 실현 가능한 점, g1 및 실현 불가능한 점, g가2 각각 비점화 점, q와1 에 어떻게 투영되는지 보여준다. 점선 및 실선 등고선은 각각 목표함수의 두 번째 항이 있는 경우와 없는 경우의 목표함수 등고선에 해당한다.

MCDM 문제 해결

MCDM 문제(설계와 평가 유형 둘 다)를 해결하기 위해 서로 다른 사상의 학교들이 발전해 왔다. 시간 경과에 따른 그들의 발전을 보여주는 영량학 연구는 Bragge, Korhonen, H. Wallenius 및 J. Wallenius[2010][18]를 참조한다.

다목적수학프로그래밍스쿨

(1) 벡터 최대화: 벡터 최대화의 목적은 원래 다중 목표 선형 프로그래밍 문제(Evans and Steuer, 1973;[19] Yu and Zeleny, 1975[20])를 위해 개발된 비첨가 세트의 근사치를 위한 것이다.

(2) 대화형 프로그래밍: 계산 단계는 의사결정 단계와 대체된다(Benayoun et al., 1971;[21] Geoffrion, Dyer 및 Feinberg, 1972;[22] Zionts and Wallenius, 1976;[23] Korhonen and Wallenius, 1988[24]) DM의 값 함수에 대한 명시적 지식은 가정하지 않는다.

목표프로그래밍

목적은 목표에 대한 무차별 목표값을 설정하고 이러한 목표에서 가중 편차를 최소화하기 위함이다. 사전 사전 편찬식 사전 편찬용 웨이트뿐만 아니라 중요 웨이트도 모두 사용되었다(Charnes and Cooper, 1961[25]).

퍼지 집합 이론가

퍼지 세트는 자데(1965)[26]에 의해 세트의 고전적 개념의 확장으로서 도입되었다. 이 아이디어는 퍼지 문제를 모델링하고 해결하기 위해 많은 MCDM 알고리즘에서 사용된다.

다중 속성 효용 이론가

다중 속성 효용 또는 가치 함수를 도출하여 가장 선호하는 대안을 식별하거나 대안 순서를 정하기 위해 사용한다. 선형 적층 효용 함수와 다중 비선형 효용 함수를 도출하기 위해 존재하는 정교한 인터뷰 기법이 사용될 수 있다(Keeney and Raiffa, 1976년[27]). 또 다른 접근방식은 의사결정자에게 가상의 대안(PAPRICA 방법; Hansen and Obler, 2008[28])을 선택하는 것과 관련된 일련의 쌍별 순위 질문을 함으로써 간접적으로 가치 기능을 이끌어내는 것이다.

프렌치 스쿨

프랑스 학교는 특히 1960년대 중반 프랑스에서 유래된 상위권 방법의 ELECTRE 계열의 의사결정 지원에 초점을 맞추고 있다. 이 방법은 베르나르 로이(Roy, 1968년[29])가 처음 제안했다.

진화다목적최적화학교(EMO)

EMO 알고리즘은 초기 모집단에서 시작하여, 한 세대에서 다음 세대로 평균 모집단을 개선하기 위해 가장 빠른 원리와 유전적 변화 연산자를 모방하도록 설계된 프로세스를 사용하여 이를 업데이트한다. 목표는 무첨가 세트를 대표하는 솔루션 모집단으로 수렴하는 것이다(Schaffer, 1984;[30] Srinivas 및 Deb, 1994[31]). 최근에는 EMO 알고리즘의 솔루션 프로세스에 선호 정보를 통합하려는 노력이 있다(Deb 및 Köksalan, 2010[32] 참조).

그레이 시스템 이론 기반 방법

1980년대에 덩줄롱은 그레이 시스템 이론(GST)과 덩의 그레이 관계 분석(GRA) 모델이라고 불리는 최초의 다목적 의사결정 모델을 제안했다. 이후, 회색 시스템 학자들은 류시펑의 절대 GRA 모델,[33] 회색 표적 의사결정(GTDM),[34] 회색 절대 결정 분석(GADA)과 같은 많은 GST 기반의 방법을 제안했다.[35]

계층 분석 프로세스(AHP)

AHP는 먼저 의사결정 문제를 하위 문제의 계층 구조로 분해한다. 그런 다음 의사결정자는 다양한 요소들의 상대적 중요성을 쌍방향 비교로 평가한다. AHP는 이러한 평가를 수치값(체중 또는 우선순위)으로 변환하여 각 대안의 점수를 계산한다(Saaty, 1980[36]). 일관성 지수는 의사결정자가 자신의 반응에서 일관성을 유지한 정도를 측정한다. AHP는 MCDA 커뮤니티의 일부 연구자들이 결함이 있다고 믿고 있는 가운데, 여기에 열거된 더 논란이 많은 기술 중 하나이다.[37] 기초 수학은 또한 상업적으로 이용 가능한 소프트웨어의 결과로 어느 정도 인기를 얻었지만 더 복잡하다[vague].

몇몇 서류들 퍼지 MCDM,[38]클래식 MCDM,[39]고 재생 energy,[40]VIKOR technique,[41]교통 systems,[42]서비스 TOPSIS method,[44]에너지 관리 problems,[45]e-learning,[46]관광과 hospitality,[47]SWARA과 WASPAS 변성 알코올. quality,[43]지속 가능한 같은 여러 분야에서 MCDM 기술의 적용을 검토했다.ds.[48]

MCDM 방법

다음과 같은 MCDM 방법을 사용할 수 있으며, 그 중 상당수는 전문화된 의사결정 소프트웨어에 의해 구현된다.[3][4]

See also

References

  1. ^ Rew, L. (1988). "Intuition in Decision-making". Journal of Nursing Scholarship. 20 (3): 150–154. doi:10.1111/j.1547-5069.1988.tb00056.x. PMID 3169833.
  2. ^ Franco, L.A.; Montibeller, G. (2010). "Problem structuring for multicriteria decision analysis interventions". Wiley Encyclopedia of Operations Research and Management Science. doi:10.1002/9780470400531.eorms0683. ISBN 9780470400531.
  3. ^ a b Weistroffer, HR, and Li, Y (2016). "Multiple criteria decision analysis software". Ch 29 in: Greco, S, Ehrgott, M and Figueira, J, eds, Multiple Criteria Decision Analysis: State of the Art Surveys Series, Springer: New York.
  4. ^ a b Amoyal, Justin (2018). "Decision analysis : Biennial survey demonstrates continuous advancement of vital tools for decision-makers, managers and analysts". OR/MS Today. doi:10.1287/orms.2018.05.13.
  5. ^ Kylili, Angeliki; Christoforou, Elias; Fokaides, Paris A.; Polycarpou, Polycarpos (2016). "Multicriteria analysis for the selection of the most appropriate energy crops: The case of Cyprus". International Journal of Sustainable Energy. 35 (1): 47–58. Bibcode:2016IJSE...35...47K. doi:10.1080/14786451.2014.898640. S2CID 108512639.
  6. ^ "Multiple Criteria Decision Making – International Society on MCDM". www.mcdmsociety.org. Archived from the original on 3 October 2017. Retrieved 26 April 2018.
  7. ^ "Welcome to EWG-MCDA website". www.cs.put.poznan.pl. Archived from the original on 7 October 2017. Retrieved 26 April 2018.
  8. ^ "Archived copy". Archived from the original on 11 August 2011. Retrieved 7 August 2011.CS1 maint: archived copy as title (link)
  9. ^ Köksalan, M., Wallenius, J., and Zionts, S. (2011). Multiple Criteria Decision Making: From Early History to the 21st Century. Singapore: World Scientific. ISBN 9789814335591.CS1 maint: multiple names: authors list (link)
  10. ^ Triantaphyllou, E. (2000). Multi-Criteria Decision Making: A Comparative Study. Dordrecht, The Netherlands: Kluwer Academic Publishers (now Springer). p. 320. ISBN 978-0-7923-6607-2. Archived from the original on 24 June 2010.
  11. ^ An Interactive Approach for Multi-Criterion Optimization, with an Application to the Operation of an Academic Department, A. M. Geoffrion, J. S. Dyer and A. Feinberg, Management Science, Vol. 19, No. 4, Application Series, Part 1 (Dec., 1972), pp. 357–368 Published by: INFORMS
  12. ^ Köksalan, M.M. and Sagala, P.N.S., M. M.; Sagala, P. N. S. (1995). "Interactive Approaches for Discrete Alternative Multiple Criteria Decision Making with Monotone Utility Functions". Management Science. 41 (7): 1158–1171. doi:10.1287/mnsc.41.7.1158.CS1 maint: multiple names: authors list (link)
  13. ^ Steuer, R.E. (1986). Multiple Criteria Optimization: Theory, Computation and Application. New York: John Wiley.
  14. ^ Karasakal, E. K. and Köksalan, M., E.; Koksalan, M. (2009). "Generating a Representative Subset of the Efficient Frontier in Multiple Criteria Decision Making". Operations Research. 57: 187–199. doi:10.1287/opre.1080.0581.CS1 maint: multiple names: authors list (link)
  15. ^ Ehrgott, M. & Gandibleux, X. (2002). "Multiobjective Combinatorial Optimization". Multiple Criteria Optimization, State of the Art Annotated Bibliographic Surveys: 369–444. Cite journal requires journal= (help)
  16. ^ Gass, S.; Saaty, T. (1955). "Parametric Objective Function Part II". Operations Research. 2 (3): 316–319. doi:10.1287/opre.2.3.316.
  17. ^ Wierzbicki, A. (1980). "The Use of Reference Objectives in Multiobjective Optimization". Multiple Criteria Decision Making Theory and Application. Lecture Notes in Economics and Mathematical Systems. Springer, Berlin. 177. pp. 468–486. doi:10.1007/978-3-642-48782-8_32. ISBN 978-3-540-09963-5.
  18. ^ Bragge, J.; Korhonen, P.; Wallenius, H.; Wallenius, J. (2010). Bibliometric Analysis of Multiple Criteria Decision Making/Multiattribute Utility Theory. IXX International MCDM Conference Proceedings, (Eds.) M. Ehrgott, B. Naujoks, T. Stewart, and J. Wallenius. Springer, Berlin. 634. pp. 259–268. doi:10.1007/978-3-642-04045-0_22. ISBN 978-3-642-04044-3.
  19. ^ Evans, J.; Steuer, R. (1973). "A Revised Simplex Method for Linear Multiple Objective Programs". Mathematical Programming. 5: 54–72. doi:10.1007/BF01580111. S2CID 32037123.
  20. ^ Yu, P.L.; Zeleny, M. (1975). "The Set of All Non-Dominated Solutions in Linear Cases and a Multicriteria Simplex Method". Journal of Mathematical Analysis and Applications. 49 (2): 430–468. doi:10.1016/0022-247X(75)90189-4.
  21. ^ Benayoun, R.; deMontgolfier, J.; Tergny, J.; Larichev, O. (1971). "Linear Programming with Multiple Objective Functions: Step-method (STEM)". Mathematical Programming. 1: 366–375. doi:10.1007/bf01584098. S2CID 29348836.
  22. ^ Geoffrion, A.; Dyer, J.; Feinberg, A. (1972). "An Interactive Approach for Multicriterion Optimization with an Application to the Operation of an Academic Department". Management Science. 19 (4–Part–1): 357–368. doi:10.1287/mnsc.19.4.357.
  23. ^ Zionts, S.; Wallenius, J. (1976). "An Interactive Programming Method for Solving the Multiple Criteria Problem". Management Science. 22 (6): 652–663. doi:10.1287/mnsc.22.6.652.
  24. ^ Korhonen, P.; Wallenius, J. (1988). "A Pareto Race". Naval Research Logistics. 35 (6): 615–623. doi:10.1002/1520-6750(198812)35:6<615::AID-NAV3220350608>3.0.CO;2-K.
  25. ^ Charnes, A. and Cooper, W.W. (1961). Management Models and Industrial Applications of Linear Programming. New York: Wiley.CS1 maint: multiple names: authors list (link)
  26. ^ Zadeh, L.A. (June 1965). "Fuzzy sets". Information and Control. San Diego. 8 (3): 338–353. doi:10.1016/S0019-9958(65)90241-X. ISSN 0019-9958. Wikidata Q25938993.
  27. ^ Keeney, R. & Raiffa, H. (1976). Decisions with Multiple Objectives: Preferences and Value Tradeoffs. New York: Wiley.
  28. ^ Hansen, Paul; Ombler, Franz (2008). "A new method for scoring additive multi-attribute value models using pairwise rankings of alternatives". Journal of Multi-Criteria Decision Analysis. 15 (3–4): 87–107. doi:10.1002/mcda.428.
  29. ^ Roy, B. (1968). "La méthode ELECTRE". Revue d'Informatique et de Recherche Opérationelle (RIRO). 8: 57–75.
  30. ^ Shaffer, J.D. (1984). Some Experiments in Machine Learning Using Vector Evaluated Genetic Algorithms, PhD thesis (phd). Nashville: Vanderbilt University.
  31. ^ Srinivas, N.; Deb, K. (1994). "Multiobjective Optimization Using Nondominated Sorting in Genetic Algorithms". Evolutionary Computation. 2 (3): 221–248. doi:10.1162/evco.1994.2.3.221. S2CID 13997318.
  32. ^ Deb, K.; Köksalan, M. (2010). "Guest Editorial Special Issue on Preference-Based Multiobjective Evolutionary Algorithms". IEEE Transactions on Evolutionary Computation. 14 (5): 669–670. doi:10.1109/TEVC.2010.2070371.
  33. ^ Liu, Sifeng (2017). Grey Data Analysis - Methods, Models and Applications. Singapore: Springer. pp. 67–104. ISBN 978-981-10-1841-1.
  34. ^ Liu, Sifeng (2013). "On Uniform Effect Measure Functions and a Weighted Multi-attribute Grey Target Decision Model". The Journal of Grey System. Research Information Ltd. (UK). 25 (1): 1–11. doi:10.1007/s40815-020-00827-8. S2CID 219090787.
  35. ^ Javed, S. A. (2020). "Grey Absolute Decision Analysis (GADA) Method for Multiple Criteria Group Decision-Making Under Uncertainty". International Journal of Fuzzy Systems. Springer. 22 (4): 1073–1090. doi:10.1007/s40815-020-00827-8. S2CID 219090787.
  36. ^ Saaty, T.L. (1980). The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation. New York: McGraw-Hill.
  37. ^ Belton, V, and Stewart, TJ (2002). Multiple Criteria Decision Analysis: An Integrated Approach, Kluwer: Boston.
  38. ^ Mardani, Abbas; Jusoh, Ahmad; Zavadskas, Edmundas Kazimieras (15 May 2015). "Fuzzy multiple criteria decision-making techniques and applications – Two decades review from 1994 to 2014". Expert Systems with Applications. 42 (8): 4126–4148. doi:10.1016/j.eswa.2015.01.003.
  39. ^ Mardani, Abbas; Jusoh, Ahmad; Nor, Khalil MD; Khalifah, Zainab; Zakwan, Norhayati; Valipour, Alireza (1 January 2015). "Multiple criteria decision-making techniques and their applications – a review of the literature from 2000 to 2014". Economic Research-Ekonomska Istraživanja. 28 (1): 516–571. doi:10.1080/1331677X.2015.1075139. ISSN 1331-677X.
  40. ^ Mardani, Abbas; Jusoh, Ahmad; Zavadskas, Edmundas Kazimieras; Cavallaro, Fausto; Khalifah, Zainab (19 October 2015). "Sustainable and Renewable Energy: An Overview of the Application of Multiple Criteria Decision Making Techniques and Approaches". Sustainability. 7 (10): 13947–13984. doi:10.3390/su71013947.
  41. ^ Mardani, Abbas; Zavadskas, Edmundas Kazimieras; Govindan, Kannan; Amat Senin, Aslan; Jusoh, Ahmad (4 January 2016). "VIKOR Technique: A Systematic Review of the State of the Art Literature on Methodologies and Applications". Sustainability. 8 (1): 37. doi:10.3390/su8010037.
  42. ^ Mardani, Abbas; Zavadskas, Edmundas Kazimieras; Khalifah, Zainab; Jusoh, Ahmad; Nor, Khalil MD (2 July 2016). "Multiple criteria decision-making techniques in transportation systems: a systematic review of the state of the art literature". Transport. 31 (3): 359–385. doi:10.3846/16484142.2015.1121517. ISSN 1648-4142.
  43. ^ Mardani, Abbas; Jusoh, Ahmad; Zavadskas, Edmundas Kazimieras; Khalifah, Zainab; Nor, Khalil MD (3 September 2015). "Application of multiple-criteria decision-making techniques and approaches to evaluating of service quality: a systematic review of the literature". Journal of Business Economics and Management. 16 (5): 1034–1068. doi:10.3846/16111699.2015.1095233. ISSN 1611-1699.
  44. ^ Zavadskas, Edmundas Kazimieras; Mardani, Abbas; Turskis, Zenonas; Jusoh, Ahmad; Nor, Khalil MD (1 May 2016). "Development of TOPSIS Method to Solve Complicated Decision-Making Problems — An Overview on Developments from 2000 to 2015". International Journal of Information Technology & Decision Making. 15 (3): 645–682. doi:10.1142/S0219622016300019. ISSN 0219-6220.
  45. ^ Mardani, Abbas; Zavadskas, Edmundas Kazimieras; Khalifah, Zainab; Zakuan, Norhayati; Jusoh, Ahmad; Nor, Khalil Md; Khoshnoudi, Masoumeh (1 May 2017). "A review of multi-criteria decision-making applications to solve energy management problems: Two decades from 1995 to 2015". Renewable and Sustainable Energy Reviews. 71: 216–256. doi:10.1016/j.rser.2016.12.053.
  46. ^ Zare, Mojtaba; Pahl, Christina; Rahnama, Hamed; Nilashi, Mehrbakhsh; Mardani, Abbas; Ibrahim, Othman; Ahmadi, Hossein (1 August 2016). "Multi-criteria decision making approach in E-learning: A systematic review and classification". Applied Soft Computing. 45: 108–128. doi:10.1016/j.asoc.2016.04.020.
  47. ^ Diedonis, Antanas. "Transformations in Business & Economics – Vol. 15, No 1 (37), 2016 – Article". www.transformations.knf.vu.lt. Archived from the original on 29 August 2017. Retrieved 29 August 2017.
  48. ^ Mardani, Abbas; Nilashi, Mehrbakhsh; Zakuan, Norhayati; Loganathan, Nanthakumar; Soheilirad, Somayeh; Saman, Muhamad Zameri Mat; Ibrahim, Othman (1 August 2017). "A systematic review and meta-Analysis of SWARA and WASPAS methods: Theory and applications with recent fuzzy developments". Applied Soft Computing. 57: 265–292. doi:10.1016/j.asoc.2017.03.045.
  49. ^ Haseli, Gholamreza; Sheikh, Reza; Sana, Shib Sankar (2020). "Base-criterion on multi-criteria decision-making method and its applications". International Journal of Management Science and Engineering Management. 15 (2): 79–88. doi:10.1080/17509653.2019.1633964. S2CID 199008586.
  50. ^ Rezaei, Jafar (2015). "Best-worst multi-criteria decision-making method". Omega. 53: 49–57. doi:10.1016/j.omega.2014.11.009.
  51. ^ Rezaei, Jafar (2016). "Best-worst multi-criteria decision-making method: Some properties and a linear model". Omega. 64: 126–130. doi:10.1016/j.omega.2015.12.001.
  52. ^ Sałabun, W. (2015). The Characteristic Objects Method: A New Distance-based Approach to Multicriteria Decision-making Problems. Journal of Multi-Criteria Decision Analysis, 22(1-2), 37-50.
  53. ^ Sałabun, W., Piegat, A. (2016). Comparative analysis of MCDM methods for the assessment of mortality in patients with acute coronary syndrome. Artificial Intelligence Review. First Online: 3 September 2016.
  54. ^ Garnett, H. M., Roos, G., & Pike, S. (2008, September). Reliable, Repeatable Assessment for Determining Value and Enhancing Efficiency and Effectiveness in Higher Education. OECD, Directorate for Education, Programme on Institutional Management in Higher Education [IMHE) Conference, Outcomes of Higher Education–Quality, Relevance and Impact.
  55. ^ Millar, L. A., McCallum, J., & Burston, L. M. (2010). Use of the conjoint value hierarchy approach to measure the value of the national continence management strategy. Australian and New Zealand Continence Journal, The, 16(3), 81.
  56. ^ Keshavarz Ghorabaee, M. et al. (2015) "Multi-Criteria Inventory Classification Using a New Method of Evaluation Based on Distance from Average Solution (EDAS) Archived 2 September 2016 at the Wayback Machine", Informatica, 26(3), 435-451.
  57. ^ Edwards, W.; Baron, F.H. (1994). "Improved simple methods for multiattribute utility measurement". Organizational Behavior and Human Decision Processes. 60: 306–325. doi:10.1006/obhd.1994.1087.
  58. ^ Zakeri, S. (2018). Ranking based on optimal points multi-criteria decision-making method. Grey Systems: Theory and Application. doi:10.1108/GS-09-2018-0040
  59. ^ Khazaei, Moein; Ramezani, Mohammad; Padash, Amin; DeTombe, Dorien (8 May 2021). "Creating shared value to redesigning IT-service products using SYRCS; Diagnosing and tackling complex problems". Information Systems and e-Business Management. doi:10.1007/s10257-021-00525-4. ISSN 1617-9846.
  60. ^ Serafim, Opricovic; Gwo-Hshiung, Tzeng (2007). "Extended VIKOR Method in Comparison with Outranking Methods". European Journal of Operational Research. 178 (2): 514–529. doi:10.1016/j.ejor.2006.01.020.
  61. ^ Joglekar, Saurabh N.; Kharkar, Rhushikesh A.; Mandavgane, Sachin A.; Kulkarni, Bhaskar D. (February 2018). "Sustainability assessment of brick work for low-cost housing: A comparison between waste based bricks and burnt clay bricks". Sustainable Cities and Society. 37: 396–406. doi:10.1016/j.scs.2017.11.025.
  62. ^ Alarcon, Bibiana; Aguado, Antonio; Manga, Resmundo; Josa, Alejandro (24 December 2010). "A Value Function for Assessing Sustainability: Application to Industrial Buildings". Sustainability. 3 (1): 35–50. doi:10.3390/su3010035.

Further reading