폰셀레-슈타이너 정리

Poncelet–Steiner theorem
임의의 주어진 점 P를 통해 평행선(h)을 직경 g으로 그립니다.BP 이외의 B, P를 통과하는 직선상의 C 지점을 선택하였습니다. (스테이너)

유클리드 기하학으로 알려진 수학의 한 분야에서, 폰셀레-슈타이너 정리는 전통적인 규칙에 추가적인 제약이 부과된 나침반과 직선형 구조에 대한 여러 결과 중 하나입니다.이 결과는 직선과 나침반으로 구성할 수 있는 것은 단 하나의 원과 그 중심이 주어진다면 직선만으로 구성할 수 있다는 것을 의미합니다.이 정리는 녹슨 나침반 등가성과 관련이 있습니다.

유클리드 구조는 주어진 요소와 요구되는 요소가 점(또는 선)인 한, 나침반과 직선을 함께 사용하여 완성할 수 있다면, 평면에 중심을 갖는 원이 하나 이상 존재한다면 직선만을 사용하여 완성할 수 있습니다.

나침반이 구조를 훨씬 쉽게 만들 수 있지만, 첫 번째 원이 그려지면 나침반의 기능적인 목적이 없다는 것을 암시합니다.모든 구성은 가능하지만, 원과 호는 나침반 없이는 그릴 수 없다는 것이 자연스럽게 이해됩니다.이것은 단지 나침반이 건축의 목적보다는 미적인 목적을 위해 사용될 수 있다는 것을 의미합니다.나침반을 사용하여 결정할 수 있는 구조를 고유하게 정의하는 모든 점은 다음과 같이 결정할 수 있습니다.

나침반의 도움 없이 직선형 도구의 사용에만 의존하는 이 정리에 따라 수행되는 구성을 슈타이너 구성이라고 합니다.슈타이너 구조는 중심이 있든 없든 평면에 이미 그려진 원을 포함하지 않는 모든 수의 원을 포함할 수 있습니다.직선형 도구가 기하학자가 사용할 수 있는 유일한 물리적 도구인 경우 평면에 존재하는 모든 종류의 고유한 모양과 곡선을 포함할 수 있습니다.반면에 폰셀레-슈타이너 정리는 원의 존재와 그 중심을 규정하고 단일 원이 나침반과 동등하다고 확언합니다.

역사

10세기에 페르시아 수학자 아부 알 와파 부즈자니 (940-998)는 일자형 가장자리와 고정된 입구가 있는 나침반, 소위 녹슨 나침반을 사용한 기하학적 구조를 고려했습니다.15세기 후반 유럽의 예술가 레오나르도 다빈치와 알브레히트 뒤러에 의해 사용되었기 때문에 이 유형의 건축물은 어느 정도 실용적인 의미가 있는 것으로 보입니다.16세기 중반에 새로운 관점이 생겨났는데, 이 관점은 개방의 크기가 고정적이지만 자의적이라고 여겨졌고, 유클리드의 건축물 중 몇 개를 얻을 수 있느냐의 문제가 무엇보다 중요했습니다.[1]

니콜 ò 폰타나 타르타글리아와의 "수학적 도전"에서 제롤라모 카르다노의 제자인 르네상스 수학자 로도비코 페라리는 "유클리드의 모든 것"(즉, 유클리드의 원소들의 첫 여섯 권의 책에 나오는 직선과 나침반 구성)이 직선과 녹슨 나침반으로 이루어질 수 있다는 것을 보여줄 수 있었습니다.10년 안에 Cardano, Tartaglia 및 Tartaglia의 제자인 Benedetti가 추가 솔루션을 확보했습니다.다음 세기 동안 이러한 해결책은 1673년 게오르크 모어가 자신의 해결책을 담은 유클리디스 큐리오시를 출판할 때까지 일반적으로 잊혀졌습니다.Mohr는 이전의 결과의 존재에 대해서만 들었고, 이것은 그가 그 문제를 연구하도록 이끌었습니다.[2]

"모든 유클리드"가 직선과 녹슨 나침반으로 수행될 수 있다는 것을 보여주는 것은 모든 직선과 나침반 구성이 직선과 녹슨 나침반으로 수행될 수 있다는 것을 증명하는 것과 같지 않습니다.그러한 증명은 직선과 나침반이 구성할 수 있는 것에 대한 공식화를 요구할 것입니다.이 기초 작업은 1822년 장 빅토르 폰셀레에 의해 제공되었는데, 모어-마스케로니 정리에 대한 모어의 연구에 동기를 부여받은 것입니다.그는 또한 직선과 녹슨 나침반이 직선과 나침반에 해당할 것이며, 또한 녹슨 나침반은 한 번만 사용하면 된다는 가능한 증거를 추측하고 제시했습니다."중심이 주어진 직선과 단일 원은 직선과 나침반과 같다"는 결과는 1833년 야코프 슈타이너에 의해 증명되었습니다.[3][1]

다른 컨스트럭트와의 관계

다양한 다른 개념, 도구, 용어 등은 종종 폰셀레-슈타이너 정리와 연관됩니다.여기에 나열된 것도 있습니다.

슈타이너 구조

슈타이너 시공이라는 용어는 일반적으로 직선형 도구만을 사용하는 기하학적 시공을 말하며, 때로는 직선형 에지 전용 시공이라고도 합니다.평면에 이미 존재하는 기하학적 물체에 대한 규정은 없으며, 그러한 조건은 미리 가정됩니다.또한 구성할 수 있는 것과 그렇지 않은 것에 대해서도 아무런 영향을 주지 않습니다.

따라서 폰셀레-슈타이너 정리를 따르는 모든 구성은 슈타이너 구성이지만, 모든 슈타이너 구성이 평면에 중심이 제공되는 원 하나의 조건만 따르는 것은 아닙니다.폰셀레-슈타이너 정리는 실제 나침반을 필요로 하지 않습니다 - 원이 평면에 존재한다고 가정됩니다 - 따라서 폰셀레-슈타이너 정리를 보여주는 여기의 모든 구성은 슈타이너 구성입니다.

녹슨 나침반

녹슨 나침반은 바늘과 연필이 너비를 조정할 수 없을 정도로 경첩이 녹슨 나침반을 묘사합니다.본질적으로, 그것은 거리가 고정되어 있고, 미리 결정되고 일정하지만 임의의 반지름의 원을 그리는 나침반입니다.원은 임의의 점에서 중앙에 그릴 수 있지만 반지름은 변경할 수 없습니다.

녹슨 나침반 구조는 제한된 건축 패러다임으로서 직선형 나침반과 고정폭 나침반을 사용할 수 있습니다.

어떤 의미에서 녹슨 나침반은 폰셀레-슈타이너 정리를 일반화하고 단순화한 것입니다.더 강력하지는 않지만 확실히 더 편리합니다.폰셀레-슈타이너 정리를 사용하려면 임의의 반지름과 중심점을 가진 단일 원을 평면에 배치해야 합니다.유일하게 그려진 원이기 때문에 녹슨 나침반으로 그렸던 것인지 아닌지는 중요하지 않고 동등합니다.그러나 일반적인 녹슨 나침반 구조의 장점은 나침반이 원하는 지점의 중심을 다시 그리는 데 반복적으로 사용될 수 있으며, 이로 인해 많은 구조를 단순화할 수 있다는 것입니다.당연히 평면에 임의로 배치된 하나의 원으로 모든 구성이 가능하다면, 일자형 나침반과 녹슨 나침반에 대해서도 같은 말을 할 수 있습니다.

직선과 녹슨 나침반은 직선과 표준 나침반으로 가능한 모든 것을 구성하는 데 충분하다고 알려져 있습니다 - 임의의 반지름의 원호는 그릴 수 없고 건설적인 것이 아닌 미적인 목적으로만 그릴 수 있다는 암시된 이해를 가지고 있습니다.역사적으로 이것은 더 강력한 결과인 퐁슬레-슈타이너 정리가 증명되었을 때 증명되었습니다.따라서 녹슨 나침반은 폰셀레-슈타이너 정리보다 약하지 않습니다.녹슨 나침반도 더 강하지 않습니다.

Poncellet-Steiner 정리는 페라리의 녹슨 나침반과 동등성을 감소시키며, 그 당시 주장이었던 1회용 나침반으로 감소시킵니다. 어떤 나침반의 직선형 구조를 독특하게 설명하는 데 필요한 모든 지점은 첫 번째 원이 배치되면 직선형 가장자리만으로 달성될 수 있습니다.폰셀레-슈타이너 정리는 녹슨 나침반 시나리오를 취하고, 처음 사용된 후에 나침반을 완전히 깨트립니다.

투영기하학

자세한 정보:투영기하학

비록 그 자체로 별개의 주제이지만, 투영 기하학의 많은 개념들이 여기 슈타이너 구조에 적용됩니다.Jakob Steiner가 나중에 증명한 이 기사의 정리를 가정했을 때, Jean-Victor Poncelet은 이 주제에 주요 기여자였습니다.투영기하학에서 개발된 많은 관련 개념에는 동시성, "무한점", 원근법, 비율 및 교차 비율, 안정점 또는 고정점, 불변점, 균질성, 선형 변환 등이 포함되지만 이에 국한되지는 않습니다.비록 투영 기하학의 주제가 직선형에만 국한되지는 않지만, 슈타이너 구조와 그 증명에 대한 철저한 처리는 투영 기하학의 배경이 필요합니다.

슈타이너 정리

만약 한 개의 원만 주어지고 다른 특별한 정보는 주어지지 않는다면, 슈타이너의 정리는 원의 중심이 원과 함께 주어져야 한다는 것을 의미합니다.이것은 그 중심이 없이 평면 내의 단 하나의 원만을 사용하여 직선의 가장자리만으로 원의 중심을 만드는 것이 불가능하다는 것을 증명함으로써 수행됩니다.프로젝티브 변환과 슈타이너의 원추형 단면을 이용한 논법이 사용됩니다.

평면에 하나의 원만 제공되는 경우, 그 중심은 직선의 가장자리만으로는 구성될 수 없습니다.

증명 내용을 ï적으로 요약하면 다음과 같습니다.직선형 도구를 사용하면 선형 투영 변환만 가능하고 선형 투영 변환은 가역적인 연산입니다.선은 임의의 선형 투영 변환 하에서 선에 투영되는 반면, 원뿔 단면은 선형 투영 변환 하에서 원뿔 단면에 투영되지만, 후자는 편심, 초점 및 원의 중심이 보존되지 않도록 치우쳐 있습니다.서로 다른 매핑 시퀀스 하에서 중심은 고유하고 가역적으로 매핑되지 않습니다.원 중심을 결정하는 데 선을 사용할 수 있는 경우에는 그렇지 않습니다.선형 변환은 가역적인 연산이므로 고유한 결과를 생성할 수 없으므로 고유한 결과가 불가능하다는 사실은 중심점 구성의 불가능성을 의미합니다.구축된 센터의 고유성은 구축을 가역적으로 만드는 추가 정보에 의존하게 됩니다.

따라서 직선으로 만들 수 있는 모든 것을 직선으로 만들 수 없고 직선으로 만들 수 있는 나침반만 만들 수는 없습니다.따라서, 폰셀레-슈타이너 정리의 요구 조건은 원 중심과 관련하여 약화될 수 없습니다.유일하게 주어진 원의 중심이 제공되지 않는 경우에는 직선의 가장자리만으로는 원을 얻을 수 없습니다.직선만으로는 불가능한 건축물이 많습니다.뭔가 더 필요하고, 중심이 확인된 원이면 충분합니다.

대체 프레임워크

또는 충분한 추가 정보와 함께 중심이 생략될 수도 있습니다.이것은 폰셀레-슈타이너 정리의 약화가 아니라, 단지 대안적인 틀일 뿐입니다.단 하나의 원을 가정하는 슈타이너 정리의 모순도 아닙니다.이러한 충분한 대체 정보의 포함은 투영 변환 하에서 매핑을 모호하게 하여 다양한 슈타이너 구조가 원 중심을 복구할 수 있게 합니다.

이러한 대안들은 각각 중심이 없는 최소한 두 개의 원과 다른 독특한 정보가 필요합니다.일부 대안에는 두 개의 동심원 또는 두 개의 교차하는 원, 세 개의 원 또는 제공된 원이 중심이 없는 다른 변형이 포함됩니다.각각의 경우 동심도, 교점, 세 번째 원 등과 같이 고유하지만 충분하지 않은 추가 기준이 각각 충족됩니다.이러한 경우 중 어느 하나라도 원의 중심을 구성할 수 있으므로 문제를 퐁슬레-슈타이너 정리 가설로 줄일 수 있습니다(평면에 원이 추가될 수 있는 추가적인 편의성과 함께).

건설적 증명 접근법

이 정리를 증명하기 위해서는 나침반과 직선의 기본 구성이 직선을 단독으로 사용함으로써 가능하다는 것을 증명해야 합니다. (원과 그 중심이 평면에 존재한다면) 이것들은 다른 모든 구성의 기초 또는 기본 단계이기 때문입니다.즉, 모든 구성은 다음과 같은 다섯 가지 기본 구성을 포함하는 일련의 단계로 작성될 수 있습니다.

  1. 두 개의 기존 점을 통해 선 만들기
  2. 한 점을 중심에 두고 다른 점을 통해 원을 만듭니다.
  3. 기존의 평행하지 않은 두 선의 교차점인 점 만들기
  4. 선과 원의 교차점에 하나 또는 두 점 만들기(교차하는 경우)
  5. 두 원의 교차점에 하나 또는 두 점을 만듭니다(교차하는 경우).

#1 – 두 점을 통과하는 선

이것은 일자 엣지만으로 할 수 있습니다.나침반도 원도 필요 없습니다.

#2 – 중심이 정의된 하나의 점을 지나는 원

원의 호는 나침반 없이는 그릴 수 없는 것으로 이해됩니다.원은 중심을 정의하는 점과 반지름에 있는 원주 상에 존재하는 점 두 개로 간주됩니다.이러한 쌍은 고유한 원을 정의하지만, 반대의 경우에는 성립하지 않습니다.우리가 증명하고자 하는 정리의 의도에 따라, 실제 원은 그려질 필요가 없고 미적인 이유로 그려질 필요가 있습니다.

#3 – 두 선의 교차점

이 공사는 직선으로 직접 할 수도 있습니다.

#4, #5 – 원과 관련된 교차로

따라서 정리를 증명하기 위해서는 4번과 5번 구조만이 직선의 가장자리와 그 중심을 가진 주어진 원을 사용하여 가능하다는 것을 증명해야 합니다.

메모들

#1이나 #3 구조에 대한 의심은 나침반을 포함하는 전통적인 구조 패러다임에 동일하게 적용될 것이므로, 폰셀레-슈타이너 정리에만 있는 우려는 아닙니다.

시공 #2는 관심을 가져서는 안됩니다.고유원이 중심점과 그 둘레의 점에 의하여 정의된다는 점은 논란의 여지가 없으나, 이는 건축목적상 충분한 정보인지, 또는 그에 의하여 그려진 원호가 필요한 것인지의 여부가 해당 문제입니다.원의 호는 원-원 및 원-선 교차의 목적으로 전통적인 구성 패러다임에서만 사용되며, 원의 호는 교차점을 찾는 데 직접 사용됩니다.따라서 만약 #4와 #5 구조가 교차하는 원의 호 없이 만족된다면, 그것은 호를 그릴 필요가 없음을 증명할 것입니다.따라서 구성 #2는 원을 고유하게 식별하는 두 점의 간단한 라벨링으로 만족됨을 의미합니다.

건설적 증명

일반적인 구조에서는 동일한 결과를 생성하는 여러 가지 변형이 종종 있습니다.그러한 변형에서 이루어진 선택은 일반성의 상실 없이 이루어질 수 있습니다.그러나 어떤 구성이 어떤 것이 실행될 수 있다는 것을 증명하기 위해 사용될 때, 이 모든 다양한 선택을 설명할 필요는 없으며 설명의 명확성을 위해 아래에는 한 가지 변형만 제공됩니다.아래에서 선택한 변형은 특정 특수 조건 하에서 단순성보다는 응용 분야에서 보편성을 위해 수행됩니다.

아래의 구성에서, 중심점 P와 그 둘레의 점 Q로 정의된 원은 원의 호가 지나가는 P(Q)로 표시됩니다.대부분의 원이 나침반으로 그려지지 않기 때문에 중심점과 원둘레점은 명시적으로 명명됩니다.정리에 따르면, 나침반이 그려진 원이 제공될 때, 그것은 단순히 주어진 원 또는 제공된 원이라고 불립니다.제공된 원은 항상 임의의 반지름을 가진 평면(즉, 일반 위치)에 임의로 배치된 것으로 가정해야 합니다.

임의의 선과 주어진 원 사이의 교점을 직접 찾을 수 있습니다.Poncelet-Steiner 정리는 평면에 이미 그려진 원을 정상적으로 처리하는 것을 금지하지 않으며, 정상적인 구성 규칙이 적용됩니다.그 정리는 단지 나침반으로 새로운 원호를 만드는 것을 금지합니다.

슈타이너 구조와 폰셀레-슈타이너 정리를 증명하는 구조는 공간에 점을 임의로 배치해야 합니다.시공 가능한 숫자의 기하학적 정의와 같은 일부 시공 패러다임에서는 이를 금지할 수 있습니다.임의의 점을 배치하는 것에 대한 그러한 제한이 있다면, 단일 원은 실제로 나침반보다 약할 수 있습니다.

몇가지 예비 공사.

아래에 포함된 위 구성 #4 및 #5를 증명하기 위해, 이들이 자주 사용되고 참조되기 때문에 필요한 몇 가지 중개 구성도 아래에서 설명됩니다.이것들은 또한 직선형 에지 전용 구조물입니다.아래의 모든 구성은 기본 구성 #1,#2,#3 및 그 이전에 나열된 다른 구성에 의존합니다.

평행선 이등분선을 가지는 선의 평행

이등분된 세그먼트가 내장된 주어진 임의의 선의 임의의 점을 통과하는 평행선 구성.

이 구성은 주어진 원을 사용할 필요가 없습니다.당연히 주어진 원의 중심을 지나는 모든 선은 암시적으로 이등분된 세그먼트를 갖습니다. 직경은 중심에 의해 이등분됩니다.이 기사의 서론에 포함된 애니메이션 GIF 파일은 이 구성을 보여줍니다. - 이등분된 직경에 의존하며 원의 호는 절대 사용되지 않습니다. - 원 없이 열거된 단계로 여기서 반복됩니다.

두 점 A와 B가 존재하는 임의의 직선 n(검은색으로 표시)이 주어지면, 그들 사이에 중간점 M이 있고, 직선 n의 평행이 만들어져야 하는 평면의 임의의 점 P가 있습니다.

  1. 선 AP(빨간색)를 작성합니다.
  2. 라인 BP(주황색)를 작성합니다.
  3. 라인 AP에서 임의의 점 R을 정의합니다.
  4. 선 BR(녹색)을 작성합니다.
  5. 라인 MR(연청색)을 구성합니다.
  6. MR 및 BP 선은 X 지점에서 교차합니다.
  7. 선 AX를 구성합니다(보라색).
  8. 선 BR과 AX는 점 Q에서 교차합니다.
  9. 원하는 병렬인 선 PQ(진청색)를 구성합니다.

일부 문헌에서 이등분 선분은 선에 존재하는 1차원 "원"으로 간주되기도 합니다.또는 일부 문헌에서는 이등분선 세그먼트를 평면과 평행하지 않고 직경을 통과하는 3차원 공간의 2차원 원으로 보기도 하며, 따라서 원둘레의 두 점에서 구성 평면과 중간점을 단순히 규정된 원 중심으로 교차합니다.

선에 이등분선 세그먼트 만들기

선이 원의 중심을 통과하는 경우 원을 통과하는 직경으로 정의된 세그먼트는 원의 중심으로 이등분됩니다.그러나 일반적인 경우 평면의 다른 선은 평면 위에 이등분된 세그먼트를 구성할 수 있습니다.이 구성은 주어진 원을 사용해야 합니다.

임의의 이등분선 세그먼트를 지정된 선에 구성합니다.

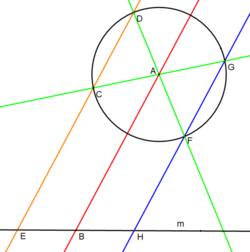
선, m(검은색) 및 A에 중심을 둔 원이 주어졌을 때, B가 중점이 되도록 선 위에 점 E, B, H를 생성하고자 합니다.

  1. 주어진 원 중심, A 및 원하는 중간점 B(임의로 선택)를 지나는 임의의 선(빨간색)을 선 m에 그립니다.
    • 빨간색 선 AB는 원의 중심을 통과하며 원의 중심으로 구분된 직경을 강조합니다.이전 구성에 따라 이 선에서 평행선을 만들 수 있습니다.
  2. 주어진 원에서 임의의 점 C를 선택합니다.
    • 편의상 원 중심을 지나는 AB의 수직에 지점이 놓이지 않아야 합니다.
  3. 빨간색 선 AB와 평행한 선(주황색)을 C를 통과합니다.
    • 점 C가 원 중심을 지나는 AB의 수직선 상에 있다면 평행선은 원과 접하게 됩니다.본 기사에 기재되지 않은 다른 방법으로 공사가 가능하지만, 그러한 점을 선택할 필요도 없습니다.
    • 이 평행선은 D에서 주어진 원과 교차합니다.
    • 이 평행선은 검은색 선대 E와도 교차하며 선분의 한쪽 끝을 정의합니다.
  4. 각각 지정된 원 중심을 통과하는 AC 및 AD 두 개의 선(녹색)을 만듭니다.
    • 이 녹색 선들은 각각 점 G와 F에서 주어진 원과 교차합니다.
  5. 선 FG(파란색)는 H에서 선 m과 교차하며 선 세그먼트의 다른 끝점을 정의합니다.
    • 이제 세그먼트 EH는 선 m과 일치하며 중간점 B를 갖습니다.

임의의 선에 대한 평행선

이 구성은 주어진 원을 사용해야 합니다.평행선 구성을 공선 이등분선 세그먼트가 아닌 모든 가능한 라인으로 일반화하기 위해서는 추가적인 정보가 필요합니다.폰셀레-슈타이너 정리에 따라, (중심을 갖는) 원이 이 구성의 선택 대상입니다.

주어진 선의 평행선을 평면의 임의의 점을 통해 구성하기 위해 우리는 두 개의 구성을 조금씩 결합합니다.

  1. 평행선을 만들 선이 존재하지 않는 경우 평행선 위에 이등분된 세그먼트가 생성되어야 합니다.
  2. 그런 다음 평행선은 공선 이등분 세그먼트를 포함하는 이전의 평행 구조에 따라 구성됩니다.

그러나 일반적으로 평행선은 이미 서로 평행한 임의의 쌍의 선으로부터 구성될 수 있습니다. 따라서 원을 사용하지 않고 대체 구성을 통해 임의의 두 선으로부터 세 번째 평행선을 만들 수 있습니다.또한 평면에 평행사변형이 있을 때마다 선의 평행사변형을 만들 수 있으며, 주어진 원을 사용하지 않아도 됩니다.

수직선 구성

수직선 구조.

이 구성은 주어진 원을 사용해야 하며 탈레스의 정리를 이용합니다.

주어진 선 m과 평면의 주어진 점 A로부터 그 점을 통해 선에 수직인 a를 구성합니다.주어진 원 O(r)이 제공됩니다.

  1. 만약 수직선 m을 만들고자 하는 원하는 선이 그림처럼 주어진 원을 통과하지 않거나 주어진 원의 중심을 통과하지 않는다면, 새로운 평행선 (빨간색으로 표시된)은 그 중심이 아니라 주어진 원을 통과하도록 임의로 만들 수 있습니다.수직선은 이 선으로부터 만들어져야 합니다.
  2. 주어진 원을 통과하지만 그 중심이 아닌 이 빨간 선은 주어진 원과 B와 C 두 점에서 교차합니다.
  3. 원 중심을 지나는 선 BO(주황색)를 그립니다.
    • 이 선은 점 D에서 주어진 원과 교차합니다.
  4. DC(연두색) 선을 그립니다.
    • 이 선은 빨간색(따라서 검은색) 선에 수직이며 BC 및 m입니다.
  5. 이전 구성을 사용하여 점 A를 통해 DC 선의 평행선을 구성합니다.
    • 원래의 검은 선의 수직선인 m은 이제 평면에 존재하며, 그 평행선은 평면의 어떤 점을 통해서도 구성될 수 있습니다.

만약 수직선이 만들어지는 선이 원 중심을 통과한다면, 슈타이너 구조를 사용하여 교차점에서 원에 대한 접선을 만드는 것이 대안적인 접근 방법이 될 것입니다.이것은 이 기사에서 설명되지 않습니다.

평면에 임의의 정사각형이 존재하는 경우, 대안적인 구조는 주어진 원 없이 수직을 구성할 수 있습니다.

세그먼트의 중간점 구성

비공선형 평행선에서 임의의 선분의 중간점 구성.

주어진 것은 이등분할 선분 AB입니다.선택적으로 평면에 평행선 m이 존재합니다.

  1. 선분 AB에 평행한 선분 m이 평면에 존재하지 않는 경우, 평면에 주어진 원(도시되지 않음)을 사용하여 이전 구성에 따라 선분 m으로 구성해야 합니다.
    • 평행선이 이미 존재하는 경우 평면에 주어진 원이 이 구성에 필요하지 않습니다.
    • 평행선은 선 세그먼트와 공선을 이루지 않는 한 평면에 임의로 배치될 수 있습니다.
  2. 평면에서 선 또는 선 세그먼트와 공선이 아닌 점 C를 임의로 선택합니다.
  3. 점 D에서 교차하는 선 AC(빨간색)를 그립니다.
  4. 점 E에서 선 m과 교차하는 선 BC(주황색)를 그립니다.
  5. 점 X에서 서로 교차하는 AE와 BD(각각 연두색)의 두 선을 그립니다.
  6. 점 M에서 세그먼트 AB와 교차하는 선 CX(파란색)를 그립니다.
    • 점 M은 세그먼트 AB의 원하는 중간 지점입니다.
    • 또한 선 CX는 세그먼트 DE를 이등분합니다.

추가적인 관점을 위해, 어떤 의미에서 이 구성은 이등분선 세그먼트로부터 평행선의 이전 구성의 변형입니다.전체적으로 동일한 선의 집합이지만 다른 순서로 구성되며 다른 초기 조건 집합에서 다른 최종 목표에 도달합니다.

대안적인 구성에서는 평면에 평행사변형이 존재할 때마다 선분을 이등분할 수 있습니다.

선 세그먼트 회전

원을 정의하려면 원 둘레의 중심과 한 점(모든 점)만 정의해야 합니다.원칙적으로 새로운 점 B'는 원 A(B)가 원 A(B')와 같도록 구성되지만 점 B는 점 B'와 같지 않습니다. 기본적으로 세그먼트 AB는 축 점 A를 중심으로 동일한 원에 대한 다른 정의점 집합에 대해 AB'로 회전됩니다.

선분의 회전에 대한 슈타이너 구조

대부분의 조건을 만족시키는 한 가지 방법은 다음과 같습니다.

  1. 선분 AB(검은색)를 그립니다.
  2. 주어진 원의 중심인 점 O를 통해 선 AB의 평행선(빨간색)을 만듭니다.
    • 평행선은 어떤 점 b에서 주어진 원과 교차합니다.
  3. Ob선과 평행하지 않은 주어진 원에서 임의로 점 b'를 선택합니다.
  4. Ob'(주황색) 선을 그립니다.
  5. 점 A(분홍색)를 통해 Ob'에 평행선을 만듭니다.
  6. 원 둘레의 점을 연결하는 선 bb'(연두색)를 그립니다.
  7. 점 B(파란색)를 통해 bb' 선의 평행선을 만듭니다.
  8. B점과 A점에서 각각 파란색과 분홍색 평행선을 교차합니다.
    • 여기는 B 지점입니다.
    • 점 B'는 원하는 점으로 선분을 회전하고 A를 중심으로 동일한 원을 정의합니다.

원하는 회전이 원과 정반대인 경우(즉, 반원 회전) 이 구성은 실패합니다.이 시나리오에 대한 한 가지 해결책은 이전과 반원 회전이 아닌 두 개의 개별 회전 구조를 사용하는 것입니다. 하나는 중간 단계로 작용합니다.두 번째 해결책은 자체적인 문제가 있을 수 있는 대체 건설 접근법을 전적으로 사용하는 것입니다.

원과 원 사이의 래디컬 축 구성

원 사이의 래디컬 축의 직선 에지 전용 구성.

이 구성은 이전에 설명된 참조된 하위 구성에 대해 주어진 원(도시되지 않음)을 사용해야 합니다.

두 개의 원 A(B)와 C(D)가 암시적으로 주어지며, 평면의 점 A, B, C, D에 의해서만 정의되고 중심은 정의되지만 나침반으로 구성되지는 않는다고 가정합니다.두 원 사이의 근축선 m(진청색)은 다음과 같이 구성할 수 있습니다.

  1. 원 중심을 지나는 AC(주황색) 선을 그립니다.
  2. 원 둘레의 점 사이에 선분 BD(빨간색)를 그립니다.
  3. 세그먼트 BD의 중간점 M을 구합니다.
  4. 세그먼트 중간 지점과 각 원 중심을 연결하는 선 AM 및 CM(모두 연두색)을 그립니다.
  5. 점 B를 통과하고 AM에 수직인 선 j(보라색)를 작성합니다.
  6. 점 D를 통과하고 CM에 수직인 선 k(진녹색)를 구성합니다.
  7. 점 X에서 선 j와 k가 교차합니다.
    • 선 j와 k가 평행한 경우 세그먼트 중간점 M은 선 AC 위에 있으며 구성이 실패합니다.대체 접근 방식이 필요합니다(아래 참조).
    • 점 X는 원 A(B), C(D) 및 M(B) 사이의 전력 중심입니다.
    • 선 j와 k는 각각 원 M(B)과 원 A(B)와 C(D) 사이의 라디칼 축입니다.
  8. 선 AC에 수직이고 점 X를 통과하는 선 m(진청색)을 작성합니다.
  9. 선 m은 원하는 라디칼 축입니다.

평행선 j와 k 사이에 교점 X가 존재하지 않아 근축 구성이 실패할 경우, 중간점 M이 AC 라인에 우연히 배치된 결과로 인해 대안적인 접근법이 필요합니다.이러한 접근 방식 중 하나는 세그먼트 AB를 축 점 A(원 A(B))를 중심으로 회전하는 것입니다.동일한 원을 정의하는 임의의 회전 AB'에 도달하면, 라디칼 축 구성은 문제없이 새로 시작할 수 있습니다.

원과 선을 교차하기 (시공 #4)

교차점의 직선 모서리 전용 구조는 선과 원 사이를 가리킵니다.

이 구성은 제공된 원, O(r)을 사용해야 합니다.

주어진 선 m(검은색)과 원 P(Q)는 나침반 구조가 아닙니다.점 A와 B인 원 P(Q)와 선 m의 교점은 다음과 같이 구성할 수 있습니다.

  1. 원을 정의하는 점을 통과하는 선 PQ(빨간색)를 그립니다.
    • 점 O가 선 PQ와 평행한 경우 세그먼트 PQ를 원의 중심점 P를 중심으로 회전해야 하며 이 구성이 새로 시작됩니다.
  2. 제공된 원의 중심 O를 통해 선 PQ의 평행선(주황색)을 구성합니다.
    • 평행선은 제공된 원과 두 점에서 교차하며, 그 중 하나는 임의로 선택됩니다: R.
  3. 두 원(즉, 나침반 구조에 의해 제공되는 것과 교차될 것)의 중심을 지나는 선 PO(연두색으로 표시)를 그립니다.
  4. 두 원의 둘레에 있는 두 점을 연결하는 선 QR(연청색)을 그립니다.
  5. 점 X에서 선 PO와 QR을 교차합니다.
    • 점 X가 선 PO와 QR이 평행하여 존재하지 않는 경우(원 P(Q)와 O(r)의 반지름이 같아지는 경우) 2단계를 다시 참조하여 교점의 대체 점 R을 선택합니다.
  6. 선 PO 상에 있지 않도록 선 m 상에 임의로 점 M을 선택하면 선 PM(분홍색)을 그립니다.
    • 시공의 단순화를 위해, 라인 PQ가 라인 m과 평행하지 않은 경우에만 라인 PM과 PQ가 일치할 수 있습니다.
  7. MX(갈색) 선을 그립니다.
  8. 제공된 원의 중심 O를 통해 PM의 평행선(진보라색)을 구성합니다.
    • 평행선은 점 N에서 선 MX와 교차합니다.
  9. 점 N을 통해 선 m의 평행선(노란색)을 만듭니다.
    • 평행선은 C점과 D점에서 제공된 원과 교차합니다.
    • 평행선이 제공된 원과 교차하지 않으면 선 m이 원 P(Q)와 교차하지 않습니다.
  10. CX와 DX를 그립니다(둘 다 짙은 파란색).
    • 이 선들은 각각 점 A와 B에서 선 m과 교차합니다.
  11. 점 A와 B는 선 m과 원 P(Q) 사이의 원하는 교점입니다.

두 개의 원이 교차하는 모습 (시공 #5)

두 원 사이의 교차점은 두 개의 이전 구성의 사소한 조합이 됩니다.

  1. 두 원 사이에 라디칼 축을 구성합니다.
  2. 앞의 작도: 기본 작도 #4를 사용하여, 래디컬 축(선)과 임의로 선택된 두 원 중 하나의 원 사이의 교점을 작도합니다.
  3. 이 점들은 원들이 교차하는 원하는 점들입니다.
    • 두 원과 라디칼 축은 모두 같은 점의 위치에서 교차합니다. 두 점은 접선인 경우 한 점, 교차하지 않는 경우 한 점은 없습니다.
    • 라디칼 축이 하나의 원과 교차하지 않으면 둘 다 교차하지 않고 두 원도 교차하지 않습니다.

한 점에서 다른 점에 중심을 둔 원(시공 #2)

두 번째 기본 구조는 원을 두 개의 점으로 정의하는 것으로, 원이 구조에 사용되기 위해 나침반으로 만들 필요가 없었습니다.즉, 원과 선이 함께 있는 원의 교차점은 원을 포함하는 모든 구성의 본질이며, 호 없이도 달성할 수 있습니다.따라서 원을 중심과 원둘레의 임의의 점으로 정의하면 원 전체를 완전히 설명하고 원과 함께 구성할 수 있습니다.이와 같이, 호는 단지 심미적인 목적으로만 사용됩니다.기본구성 2번을 만족하였습니다.

결론

5개의 기본 구성 모두 직선의 가장자리만으로 달성할 수 있는 것으로 나타났으므로, 중심을 갖는 단일 원이 평면에 놓인다면, 이는 폰셀레-슈타이너 정리를 증명합니다.

기타 제한공사 유형

나침반과 관련된 제한된 구조물

폰셀레-슈타이너 정리는 어떤 나침반과 직선형 구조도 나침반만으로 수행할 수 있다는 모어-마스케로니 정리와 대조될 수 있습니다.

녹슨 나침반 제한은 고정된 반지름의 원을 만들어낸다면 나침반을 사용할 수 있게 해줍니다.녹슨 나침반 구조가 10세기부터 탐구되었고, 17세기까지 유클리드의 모든 구조가 녹슨 나침반으로 구성될 수 있는 것으로 보여졌지만, 폰셀레-슈타이너 정리는 녹슨 나침반과 직선이 함께 있는 것이 유클리드의 모든 구조에 충분하다는 것을 증명합니다.실제로 녹슨 나침반은 직선과 단일 원 위에서만 구조를 단순화하는 도구가 됩니다.반대로 볼 때, 폰셀레-슈타이너 정리는 녹슨 나침반의 폭을 고정시킬 뿐만 아니라, 나침반이 처음 사용된 후에 깨지도록 보장합니다.

제한된 슈타이너 구조

중심을 갖는 하나의 원이 제공하는 요건은 그 이후로 대체적이지만 동등하게 제한적인 조건을 포함하도록 일반화되거나 강화되었습니다.

이러한 대안 중 하나에서는 원 전체가 전혀 필요하지 않습니다.1904년 프란체스코 세베리는 중심과 함께 어떤 작은 호라도 충분하다는 것을 증명했습니다.[4]이 공사는 첫 번째 원이 완성되기 전에는 녹슨 나침반을 부수지만, 시작된 후에는 원의 원호의 일부 연속적인 부분을 평면에 그리고, 여전히 모든 공사가 가능합니다.따라서 폰셀레-슈타이너 정리를 가설로 하는 조건은 실제로 약화될 수 있지만, 원호의 완전성에 관해서만 가능하고, 중심에 대해서는 슈타이너 정리에 따라 가능하지 않습니다.

다른 두 가지 대안에서는 두 개의 동심원 또는 두 개의 서로 다른 교차하는 원이 주어지면 중심이 완전히 생략될 수 있습니다. 그 중 두 개의 교차점과 한 개의 교차점(접선원)이 있습니다.이러한 시나리오 중 어느 하나라도 중심을 구성하여 시나리오를 원래의 가설로 축소할 수 있습니다.

또 다른 변형이 존재합니다.교차하지 않는 두 개의 원은 (중심이 없는) 두 개로 충분합니다. 이 원들을 통과하는 중심선 또는 이들 사이의 라디칼 축에 적어도 한 점이 주어진다면 말입니다.또한 세 개의 교차하지 않는 원을 가지는 것으로도 충분합니다.[5]하나의 중심이 구성되면 시나리오는 다시 퐁슬레-슈타이너 정리의 원래 가설로 줄어듭니다.

앞에서 언급한 각각의 시나리오에서, 원의 호가 교차하지 않을 때마다 원 교차점이 명시적으로 주어진다면, 세베리의 1904년 정리에 따르면, 원 호의 완전성은 필요하지 않습니다.원호의 완전성은 중복됩니다.

다른 독특한 시나리오들은 의심할 여지 없이 존재합니다.이것은 모든 가능성의 목록이 아닙니다.

확장형, 해방형, 또는 신경증, 구조

건설 규칙을 더 제한하는 대신에, 그 제한을 완화하는 것을 연구하는 것은 동등한 관심사입니다.이를 확장 구조물이라고 부르기도 합니다.기하학자들이 나침반 전용, 일자 전용, 녹슨 나침반 등과 같은 전통적인 건축 규칙에 추가적인 제약을 가했을 때 무엇이 (그리고 어떻게) 건설할 수 있는지를 연구한 것과 같습니다.- 그들은 또한 전통적인 건설 규칙에 내재된 자연적인 제약이 완화될 때 아직 가능하지 않은 건설이 무엇이 되는지 연구했습니다."구성 가능한 것", "어떻게 구성할 수 있을까", "깨어져야 할 전통적인 규칙 중 가장 적은 것은 무엇인가", "필요한 가장 간단한 도구는 무엇인가", "어떤 겉보기에 다른 도구가 동등한가" 등의 질문이 나옵니다.

임의의 각도는 예를 들어 전통적인 나침반과 직선 규칙을 사용하여 분할할 수 없지만 평면에 타원의 추가 도구를 허용하면 분할이 가능합니다.각도 분할, 정육면체 두 배, 원의 사각형, 입방근 찾기 등과 같은 전통적인 문제 중 일부는 확장된 도구 세트를 사용하여 해결되었습니다.일반적으로 구성 가능한 것의 범위를 확장하기 위해 연구되는 대상은 다음과 같습니다.

고대의 기하학자들은 나침반과 직선형 구조물(평면형 구조물로 알려짐)을 이상적이고 선호하는 것으로 여겼습니다.두 번째로, 그들은 원 이외의 평면에 원뿔형 단면을 사용하는 것을 포함하는 견고한 건축물을 선호했습니다.그들은 세 번째로 평면에서 임의의 매끄러운 곡선을 사용하는 것을 선호했고, 신경 사용(대체 물리적 핸드헬드 도구)을 사용하는 것을 가장 선호했습니다.적어도 서양 세계의 고대 기하학자들이 심지어 종이 접기를 고려했을지는 의문입니다.

노이시스(Neusis) 또는 노이시스(Neusis) 구조라는 용어는 고대 기하학자들이 사용한 특정한 도구나 방법을 의미할 수도 있습니다.

근사치

모든 구성 패러다임에서 모든 구성은 나침반과 직선의 제한된 수의 적용으로 종료되어야 하며 정확한 의도된 결과를 생성해야 한다는 암묵적인 규칙을 지적할 필요가 있습니다.이 두 조건 중 하나를 완화하면 전체적인 논의가 이루어질 수 있습니다.

그렇지 않은 경우 구성할 수 없는 그림의 경우:

  • 반복적인 접근법을 사용하여 나침반과 직선만을 사용하여 구조를 미리 결정된 수준의 정밀도로 근사화할 수 있습니다.
  • 이 수렴 과정의 무한한 한계에서는 정확한 시공이 가능할 수 있지만, 무한한 시공이 필요합니다.

예를 들어, 각도 분할은 정확히 무한한 각도 이등분 시퀀스를 사용하여 수행될 수 있습니다.시공이 일부 유한 반복에서 종료되는 경우, 임의의 정밀도로 정확한 단면 근사치를 얻을 수 있습니다.각 점, 선 또는 원은 유효한 구성이지만, 목표로 하는 근사치는 결코 진정으로 달성될 수 없습니다.

물론 구성할 수 없는 도형에 대해 합리적인 근사치를 제공하는 정확한 구성 가능한 도형이 있습니다. 7각형의 근사치에 대해 비교적 간단한 반복적이지 않은 구성과 같이 말입니다.

참고 항목

메모들

  1. ^ a b 이브 1963, 페이지 205
  2. ^ Retz & Keihn 1989, p.195
  3. ^ Jacob Steiner (1833). Die geometrischen Konstructionen, ausgeführt mittelst der geraden Linie und eines festen Kreises, als Lehrgegenstand auf höheren Unterrichts-Anstalten und zur praktischen Benutzung (in German). Berlin: Ferdinand Dümmler. Retrieved 2 April 2013.
  4. ^ Retz & Keihn 1989, 페이지 196
  5. ^ 볼프람의 수학 세계

참고문헌

  • Eves, Howard (1963), A Survey of Geometry /Volume one, Allyn and Bacon
  • Retz, Merlyn; Keihn, Meta Darlene (1989), "Compass and Straightedge Constructions", Historical Topics for the Mathematics Classroom, National Council of Teachers of Mathematics (NCTM), pp. 192–196, ISBN 9780873532815

추가열람

외부 링크