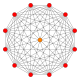
도데카곤
Dodecagon정규 도데카곤
일반 도데각형은 길이가 같은 면과 크기가 같은 내부 각도를 가진 형상이다. 12행의 반사대칭과 12행의 회전대칭이 있다. 일반 도데카곤은 Schléfli 기호 {12}로 표시되며 잘린 육각형, t{6} 또는 두 번 잘린 삼각형 tt{3}로 구성할 수 있다. 일반 도데카곤의 각 꼭지점에서의 내부 각도는 150°이다.
면적
측면 길이 a의 정규 도표 영역은 다음과 같다.
그리고 apothem r (기각된 그림 참조)의 관점에서 그 면적은 다음과 같다.
도데카곤의 스팬 S는 두 평행한 면 사이의 거리로, 아포템의 두 배와 같다. 면적에 대한 간단한 공식(측면 길이 및 범위 지정)은 다음과 같다.
이는 삼각관계로 확인할 수 있다.
둘레
회음부 측면에서 일반 도표형의 둘레는 다음과 같다.[2]
아포템의 측면에서 경계는 다음과 같다.
이 계수는 면적에 대한 아포템 방정식에서 발견된 계수의 두 배가 된다.[3]
도데카곤 건설
12 = 22 × 3과 같이, 일반 도데카곤은 나침반과 직선 구조를 사용하여 구성할 수 있다.
일정한 옆길로 애니메이션. (구성은 주어진 측면 길이에 있는 팔각형 구조와 매우 유사하다.
해부
| 12시 15분 | 15 롬브 해부 | 60 롬브 해부 | |||
|---|---|---|---|---|---|
 |  |  |  |  | |
 |  |  | |||
Coxeter는 모든 조노헤드론(상대방이 평행하고 길이가 같은 2m-곤)을 m(m-1)/2 평행그램으로 해부할 수 있다고 말한다.[4] 특히 면적이 고르게 많은 일반 다각형의 경우, 이 경우 평행사변형은 모두 rhombi이다. 일반 도데카곤의 경우 m=6이며, 15:3제곱, 6폭 30° 롬, 6폭 15° 롬으로 나눌 수 있다. 이 분해는 페트리 폴리곤의 6-큐브 투영을 기반으로 하며, 240개의 면 중 15개가 있다. OEIS 시퀀스 A006245는 최대 12배의 회전과 반사되는 치랄 형태를 포함하여 908개의 솔루션으로 정의한다.
 6시 15분 |  |  |  |  |  |
 |  |  |  |  |  |
수학적 조작 패턴 블록이 사용되는 방법 중 하나는 많은 다른 도데카곤을 만드는 것이다.[5] 이들은 롬비 전파와 관련이 있는데, 3 60° 롬비가 육각형, 반헥사곤 사다리꼴로 합쳐지거나 2개의 등각형 삼각형으로 나뉜다.
| 정규 | 무늬 블록 | |
|---|---|---|
 |  |  |
대칭
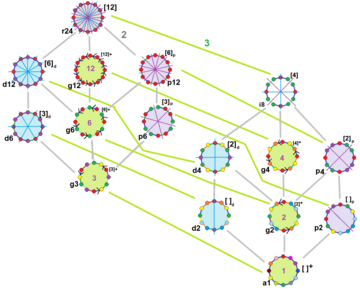
일반 도데카곤은 Dih12 대칭, 순서 24이다. 15개의 구별되는 부분군 분리와 순환 대칭이 있다. 각 부분군 대칭은 불규칙한 형태에 대해 하나 이상의 자유도를 허용한다. g12 부분군만 자유도는 없지만 지시된 가장자리로 볼 수 있다.
발생
타일링
일반 도데각형은 평면 꼭지점을 다른 일반 다각형으로 4가지 방법으로 채울 수 있다.
다음은 정점 구성에 의해 정의된 정기적인 도데카곤을 사용하는 3가지 주기적 평면 기울기 예시:
| 1시 30분 | 2시 30분 | |
|---|---|---|
 3.12.12 | 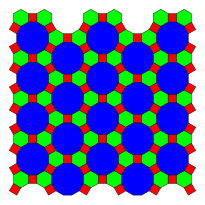 4.6.12 |  3.12.12; 3.4.3.12 |
스큐 도데카곤
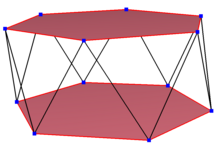
스큐 도데카곤은 12개의 정점과 가장자리가 있지만 동일한 평면에 존재하지 않는 스큐 폴리곤이다. 그러한 십이각형의 내부는 일반적으로 정의되어 있지 않다. 꼬치 지그재그 도데카곤은 두 평면이 번갈아 가며 정점을 가지고 있다.
일반 스큐 도데카곤은 가장자리 길이가 같은 정점 변환이다. 3차원에서는 지그재그 스큐 도데카곤이 될 것이며, 동일한5d D, [2+,10] 대칭, 순서 20을 가진 육각형 항정신병증의 정점과 측면 가장자리에서 볼 수 있다. 도치형 항정신병, s{2,24/5} 및 도치형 교차 항정신병, s{2,24/7}도 정규 스큐 도데카곤을 가지고 있다.
페트리 폴리곤
일반 도데카곤은 콕시터 평면에서 직교 투영으로 보이는 많은 고차원 다면체의 페트리 폴리곤이다. 4차원의 예로는 24셀, 스너브 24셀, 6-6 듀오프라미드, 6-6 듀오프라미드가 있다. 6차원 6-큐브, 6-정맥, 22122, 1 그것은 또한 웅장한 120 셀과 훌륭한 용접된 120 셀을 위한 Petrie 폴리곤이다.
관련숫자
도데카그램은 기호 {12/n}로 표현되는 12면 별 다각형이다. 정점을 사용하지만 5번째 지점마다 연결하는 정점을 사용하여 {12/5}의 정규 항성 다각형이 하나 있다. 또한 세 가지 화합물이 있는데, {12/2}은(는) 두 개의 육각형으로 2{6}로, {12/3}은(는) 세 칸으로 3{4}로, {12/4}은(는) 4개의 삼각형으로 4{3}로, {12/6}은(는) 6개의 퇴화 디곤으로 6{2}로 감소한다.
일반 도데카곤과 도데카그램의 더 깊은 절단은 같은 간격의 정점과 두 개의 가장자리 길이를 가진 등각(Vertex-transitive) 중간 항성 폴리곤 형태를 생성할 수 있다. 잘린 육각형은 도데각형, t{6}={12}. {6/5}(으)로 반전된 quasitrunculated 육각형은 dodecagram: t{6/5}={12/5}.[7]
사용 중인 예
블록 대문자에서는 E, H, X(및 슬래브 세리프 글꼴의 I) 문자의 윤곽이 도십각형이다. 크로스는 쉐보레 자동차부문의 로고처럼 도데카곤이다.

그 규칙적인 십팔각형은 많은 건물에서 두드러지게 나타난다. 토레 델 오로(Torre del Oro)는 알모하드 왕조가 건설한 스페인 남부 세빌의 도십각형 군사 감시탑이다. 스페인 세고비아에 있는 13세기 초 베라 크루즈 교회는 도십팔각형이다. 또 다른 예는 이탈리아 스펠로(Crhelo)에 있는 포르타 디 베네르(Venus's Gate)인데, BC 1세기에 지어진 두 개의 십각형 탑이 있는데, 이 탑은 "Propertius's Tower"라고 불린다.
일반 도각형 동전은 다음을 포함한다.
- 영국인들은 1937년부터 1971년까지 3페니짜리 지폐가 합법적인 입찰이 중단되었던 시기였다.
- 2017년 선보인 브리티시 원파운드 코인.
- 오스트레일리아 50센트 동전
- 피지안 50센트
- 1974년 이후 통안 50세니티
- 솔로몬 제도 50센트
- 크로아티아 25 쿠나
- 루마니아 5000 레이, 2001-2005
- 캐나다 페니, 1982-1996년
- 남베트남 20 , 1968ng, 1968–1975
- 잠비아 50ngwee, 1969-1992
- 말라위 50탐발라, 1986-1995
- 멕시코 20센타보, 1992-2009
참고 항목
메모들
- ^ Wolfram 시연 프로젝트에 대한 Kürschak의 기하학적 증거를 참조하십시오.
- ^ 평면 기하학: Clarence Addison Willis B, (1922) Blakiston의 Son & Company, 페이지 249 [1]
- ^ 존 플레이페어, 윌리엄 월리스, 존 데이비슨, (1814) 벨 & 브래드퓨트, 페이지 243 [2]
- ^ Coxeter, 수학 오락 및 에세이, 13판, 페이지 141
- ^ mathforum.org의 "Doin' Da' Dodeca"
- ^ 존 H. 콘웨이, 하이디 버기엘, 차임 굿맨 스트라우스(2008) 사물의 대칭성, ISBN978-1-56881-220-5 (20장, 일반화 셰플리 기호, 다각형 대칭 유형 275-278)
- ^ 수학의 가벼운 면: 레크리에이션 수학과 그 역사에 관한 외젠파워스 기념회의 진행, (1994) 다각형의 변형, 브란코 그룬바움
외부 링크
- Weisstein, Eric W. "Dodecagon". MathWorld.
- 쿠르샤크의 기와 정리
- 대화형 애니메이션을 사용한 doDecagon의 정의 및 속성
- 패턴 블록을 사용한 교실의 일반 문서 목록