스너브 24셀

스너브 24셀
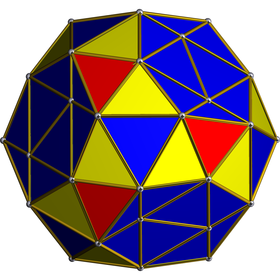정사영 하나의 이코사면체의 하이퍼플레인 중심.
유형	제복4폴리토프
슐레플리 기호^[1]	s{3,4,3} sr{3,4} s{3^1,1,1}
콕시터딘킨 도표	또는 또는
세포	144	96 3.3.3 (1998년) 24 3.3.3 24 3.3.3.3.3
얼굴	480 {3}
가장자리	432
정점	96
정점수	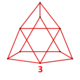(삼면체)
대칭군	[3⁺,4,3],1/2F₄ 576호 주문 [(3,3,4),⁺ 1/2B₄, 주문 192 [3^1,1,1],⁺ 1/2D₄, 주문 96
특성.	볼록하게 하다
균일지수	30 31 32

정점 그림:삼면체
8면:

5 3.3.3 및 3 3.3.3.3

기하학에서 snub 24-cell 또는 snub disicositetrachoron은 120개의 정규 사면체와 24개의 이면체로 구성된 볼록한 통일 4-폴리토프다.각 꼭지점마다 5개의 사두면체와 3개의 이코사면체가 만난다.총 480개의 삼각형 면, 432개의 가장자리, 96개의 꼭지점을 가지고 있다.600-셀에서 그것을 만들 수 있는 것은, 선택된 일부의 고드름 피라미드를 줄이고 그것의 고드름 기반만 남겨두면 480개의 사두체를 제거하고 24개의 고드름으로 교체하는 것이다.

토폴로지로는 가장 높은 대칭인 [3⁺,4,3] 아래에 잘린 24세포의 교대로 24개의 피리토헤드라(T대칭이_h 있는 이코사헤드론), 24개의 일반 사트라헤드라와 96개의 삼각 피라미드를 포함하고 있다.

반정형 폴리토프

소럴드 고셋이 1900년 논문에서 발견한 플라토닉 고형분인 두 개 이상의 세포로 만든 세 개의 반정형 4폴리탑 중 하나이다.그는 이것을 사면체와 이코사면체 세포로 만들어졌다는 이유로 측량체라고 불렀다. (다른 두 개는 바로 수정한 5세포와 600세포가 있다.)

대체 이름

스너브 이코시테트라초론
스너브 데미티세랙트
세미 스너브 폴리옥타헤드론(존 콘웨이)^[2]
사디 (Jonathan Bowers: snub disicositetrachoron용)
Tetricosaheadric Thorold Gosset, 1900년^[3]

기하학

좌표

길이 2의 가장자리가 있는 4-공간 원점을 중심으로 한 스너브 24-셀의 정점은 고른 순열을 취하여 구한다.

(0, ±1, ±φ, ±φ²)

(여기서 φ = (1+√5)/2 ≈ 1.1618은 황금비율이다.

이 96개의 정점들은 24셀의 96개의 가장자리 각각을 황금비율로 분할함으로써 찾을 수 있는데, 이는 이코사헤드론 또는 "스너브 옥타헤드론"의 12 정점을 황금비율로 분할하여 산출할 수 있는 것과 거의 같은 방식이다.이것은 먼저 24 셀의 가장자리를 따라 벡터를 배치하여 각 2차원 표면이 사이클로 경계를 이루도록 한 다음, 마찬가지로 벡터 방향을 따라 각 가장자리를 황금비로 분할함으로써 이루어질 수 있다.^[4]이것은 아래에 설명된 24-셀의 스너브 잘림과 동일하다.

스너브 24 셀의 96 정점은 24 셀의 24 정점과 함께 600 셀의 120 정점을 형성한다.

시공

스너브 24 셀은 24 셀에서 특별한 형태의 잘림 형태로 파생된다.

절단은 정점까지 입사하는 가장자리를 절단하여 정점을 제거하며, 절단의 형태는 절단이 이루어지는 가장자리의 위치에 따라 다르다.24세포의 일반적인 자르기에는 재인정된 24세포(각 가장자리를 중간점에서 자르고, 24큐브와 24큐방아헤드라로 경계한 폴리토프를 생성함)와 잘린 24셀(각 가장자리의 3분의 1을 정점에서 자르고, 24큐브와 24잘린 옥타헤드라로 경계된 폴리토프를 생성함)이 있다.24-셀의 정점 그림은 정점이고 절단은 정점에서 등거리기 때문에 이러한 절개에서는 정점이 제거된 정점 대신 정점이 생성된다.

24 셀의^[5] 스너브 잘라낸 부분은 각 가장자리를 두 개의 황금 섹션으로 절단한다(큰 섹션은 작은 섹션에 대해 황금 비율 ~ 1.618, 원래 가장자리는 큰 섹션에 대한 황금 비율).절단은 일관적인 결과를 얻기 위해 각 꼭지점에 부딪히는 대체 가장자리의 다른 방향으로 이루어져야 한다.24-셀에서 정점에 부닥친 가장자리는 정점 그림의 8 반지름이다.정육면체의 대체 반지름을 선택하는 유일한 방법은 정점에서 길이의 작은 부분에서 잘라낼 4면체(정육면체 내 포함)의 4 반지름과 정점에서 길이의 큰 부분에서 잘라낼 반대 4 반지름(정육면체에 새겨질 수 있는 다른 4면체 중)을 선택하는 것이다.물론 두 가지 방법이 있다; 둘 다 정육면체보다는 제거된 정점 대신 다섯 개의 정사각형 성단을 생산한다.

이 건축은 3차원에서 유추한다: 같은 방법으로 팔면체로부터 이코사면체(snub oxaheadron)를 건설하는 것이다.^[6]그것이 스너브-24 세포의 이코사헤드라가 잘리는 동안 24세포의 옥타헤드라에서 생성되는 방법이다.

스너브 24 셀은 교체 작업에 의해 잘린 24 셀과 관련이 있다.정점의 절반은 삭제되고 24개의 잘린 옥타헤드론 세포는 24개의 아이코사헤드론 세포가 되며, 24개의 정육면체는 24개의 4면체 세포가 되며, 96개의 삭제된 정점 공극은 96개의 4면체 세포를 새로 만든다.

직교₄ 투영, F Coxeter 평면

스너브 24셀	600셀

스너브 24 셀은 또한 600 셀의 특정한 감소에 의해 구성될 수 있다: 24 셀의 그것들에 해당하는 600 셀에서 24 정점을 제거한 다음 나머지 정점의 볼록한 선체를 취함으로써.이것은 600세포에서 24개의 이코사이드 피라미드를 제거하는 것과 같다.

구조

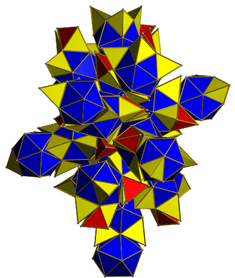청색 이코사헤드라가 있는 스너브 24세포 그물, 빨간색과 노란색 사트라헤드라가 있는 그물.

고드름 세포는 얼굴을 맞대고 맞닿아 있으며, 이들 사이의 공극은 5개의 4면세포로 이루어진 군집으로 채워진다.

각 고드름 세포는 내접하는 팔면체에 해당하는 위치에서 8개의 삼각형 면에 8개의 다른 고드름 세포와 결합된다.나머지 삼각형 면은 사면세포와 결합되는데, 사면세포는 고면세포의 가장자리를 공유하는 쌍으로 발생한다.

사면세포는 각각 96개의 황색세포와 24개의 적색세포로 구성된 두 그룹으로 나눌 수 있다(그물 그림에서 색칠된 것).각각의 황색 사면세포는 삼각면을 통해 3개의 청색 고면세포와 1개의 적색 사면세포에 연결되며, 각 적색 사면세포는 4개의 황색 사면세포에 연결된다.따라서 사면세포는 5개의 군집(빨간 중심 세포 주위로 네 개의 노란 세포가 마주보고 있으며, 각각의 빨간색/노란색 쌍이 다른 하이퍼플레인에 놓여 있다)으로 발생한다.5개의 빨간 중심 사면체는 6개의 가장자리와 다른 고면세포, 그리고 고면세포에서 그 가장자리를 공유하는 노란 사면세포 쌍과 각각을 공유한다.

대칭

스너브 24 셀은 대체되는 콕시터 그룹에 와이트오프 구조에 기반한 세 개의 정점 변환 색상을 가지고 있다.F는₄ 24개의 서로 바꿀 수 있는 이코사헤드라를 정의하고, B₄ 그룹은 8:16 카운트로 이코사헤드라의 두 그룹을 정의하고, 마지막으로 D₄ 그룹은 8:8:8 카운트로 이코사헤드라의 세 그룹을 정의한다.

대칭 (주문)	건설명	콕시터-딘킨 도표 확장 슐래플리 기호	세포 (정점 그림에서 면과 같은 색)
1/2F₄ [3⁺,4,3] (576)	스너브 24셀	s{3,4,3}	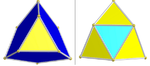24개 아이코사헤드라 1세트(파란색) 테트라헤드라 2세트: 96(노란색)과 24(사이안)
1/2B₄ [(3,3)⁺,4] (192)	스너브 정류 16셀	sr{3,4}	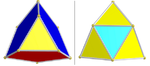이코사헤드라 2세트: 8, 16개(빨간색 및 파란색) 테트라헤드라 2세트: 96(노란색)과 24(사이안)
1/2D₄ [3^1,1,1]⁺ (96)	옴니스누브 데미테서락트	s{3^1,1,1}	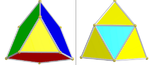이코사헤드라 3세트(빨간색, 녹색, 파랑색) 테트라헤드라 2세트: 96(노란색)과 24(사이안)

반대로, 600 셀은 24개의 이코사이드 피라미드로 증축함으로써 24개의 스너브 24 셀로부터 건설될 수 있다.

투영

직교 투영

맞춤법 투사
콕시터 평면	F₄	B₄
그래프
치측 대칭	[12]⁺	[8/2]
콕시터 평면	D₄ / B₃ / A₂	B₂ / A₃
그래프
치측 대칭	[6]⁺	[4]

투시 투영

투시 투영
원근 투영은 정점 중심 반경의 5배 거리에 4D 관점을 배치한 고두면 셀을 중심으로 한다.가장 가까운 이코사면 세포는 고체 색으로 렌더링되고, 다른 세포는 가장자리 바깥에 있다.4D 관점을 벗어난 셀을 도려내 시각적 혼란을 줄인다.	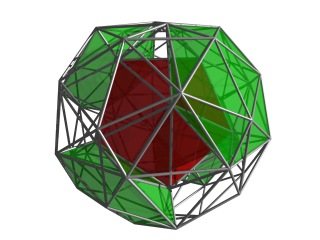같은 투영법으로, 현재 8개의 이코사면 세포 중 4개가 중앙 세포에 녹색으로 둘러싸여 있다.
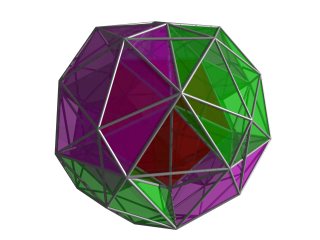위와 같은 투영법으로, 이제 다른 4개의 이코사면 세포가 자홍색으로 표시된 중심 세포를 둘러싸고 있다.이 이미지의 애니메이션 버전은 이 세포들의 레이아웃을 잘 보여준다. 이러한 특정한 관점에서, 사면세포를 포함하는 틈새 중 하나를 볼 수 있다.이 틈새 각각은 여기 보이는 것이 아닌 5개의 사면세포로 채워진다.	위와 같은 투영법으로, 이제 중앙 사면세포가 채워진 틈새로.이 사면세포는 4개의 다른 사면세포와 결합되는데, 그 중 2개는 이 이미지에서 보이는 두 개의 간격을 채운다.나머지 두 개는 각각 녹색 사면세포, 자면세포, 중앙세포 사이에 누런 사면세포의 왼쪽과 오른쪽으로 놓여 있다. 이러한 이미지에서 4D 관점에서 멀리 향하는 셀이 도태되었다는 점에 유의하십시오. 따라서 여기서 설명되는 셀은 총 1 + 8 + 6 + 24 = 39개뿐입니다.다른 세포들은 스너브 24세포의 반대편에 놓여있다.그들 중 한 곳의 가장자리 윤곽의 일부인, 이코사면 세포는 노란 4면체 위에 걸쳐서 여기서 확인할 수 있다.
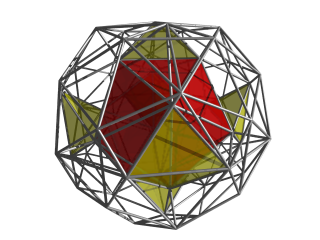이 이미지에서 가장 가까운 이두면세포와 이전 이미지에서 가장 가까운 6개의 노란 4면세포만 보인다.	이제 중앙 이두상세포와 결합된 12개의 사두상세포와 6개의 노란 사두상세포가 보인다.이들 세포는 각각 중앙 이코사면체와 앞서 보여진 다른 이코사면 세포 2개로 둘러싸여 있다.
마지막으로, 6개의 황색 사면세포에 결합한 나머지 12개의 사면세포가 여기에 나타난다.이 세포들은 앞에서 보여진 8개의 이코사이드 세포와 함께 중심 세포와 최소한 1개의 꼭지점을 공유하는 모든 세포로 구성된다.

참고 항목

스너브 24셀 벌집

메모들

^ 클라이칭, (s3s4o3o - sadi)
^ 2008년 콘웨이, p.401 고셋의 반스너브 폴리오크헤드론
^ 고셋, 1900년
^ Coxeter, 일반 폴리토페스, 1973년
^ Coxeter 1973, 페이지 151–153, 제8.4조.스너브 {3,4,3}.
^ Coxeter 1973, 페이지 50-52, 제3.7. sfn 오류: 목표 없음: CITREFCoxeter1973(도움말)

참조

T. 고셋:수학의 메신저 맥밀런, 1900년 n차원의 정규 및 반정규격 수치에 관한 연구, 1900년
H. S. M. Coxeter (1973). Regular Polytopes. New York: Dover Publications Inc. pp. 151–152, 156–157.
Snub icositetrachoron - 데이터 및 이미지
3. icositetrachoron (24세포) - 모델 31, George Olshevsky에 기초한 볼록 균일 폴리초라.
Klitzing, Richard. "4D uniform polytopes (polychora) s3s4o3o - sadi".
존 H. 콘웨이, 하이디 버기엘, 차임 굿맨-스트라스, 2008년 사물의 대칭성, ISBN 978-1-56881-220-5 (제26장)
Snub 24-Cell Coxeter-Weyl 그룹 W(D4) [1], Mehmet Koca, Nazife Ozdes Koca, Muataz Al-Barwani(2012);인트 J. 검.메서드 모드.09, 1250068(2012)

외부 링크

인쇄 #11: 스너브 이코시테트라초론 그물, 조지 올셰프스키

v t 치수 2-10의 기본 볼록형 일반 및 균일한 폴리토프
가족	A_n	B_n	I₂(p) / D_n	E₆ / E₇ / E₈ / F₄ / G₂	H_n
정규 다각형	삼각형	사각형	p-곤	육각형	펜타곤
균일다면체	사면체	옥타헤드론 • 큐브	데미큐브		도데카헤드론 • 이코사헤드론
균일 폴리초론	펜타코론	16-셀 • 테세락트	데미테세락트	24셀	120 셀 • 600 셀
제복5폴리토프	5와섹스	5정형 • 5정형	5데미큐브
제복6폴리토프	6-630x	6-정통 • 6-118	6데미큐브	1₂₂ • 2₂₁
제복7폴리토프	7시 15분	7정맥 • 7정맥	7데미큐브	1₃₂ • 2₃₁ • 3₂₁
제복8폴리토프	8시 15분	8정형 • 8정형	8데미큐브	1₄₂ • 2₄₁ • 4₂₁
제복9폴리토프	9시 15분	9-정통 • 9-11	9데미큐브
균일 10폴리토프	10센트짜리	10정형 • 10정형	10데미큐브
균일 n폴리토프	n-제곱스	n-직관 • n-직관	n-데미큐브	1_k2 • 2_k1 • k₂₁	n-자갈 폴리토프
주제: 폴리토페 패밀리 • 일반 폴리토페 • 일반 폴리토페 및 화합물 목록

[1] 클라이칭, (s3s4o3o - sadi)

[2] 2008년 콘웨이, p.401 고셋의 반스너브 폴리오크헤드론

[3] 고셋, 1900년

[4] Coxeter, 일반 폴리토페스, 1973년

[FOOTNOTECoxeter1973151–153§8.4-5] Coxeter 1973, 페이지 151–153, 제8.4조.스너브 {3,4,3}.

[FOOTNOTECoxeter197350–52§3.7-6] Coxeter 1973, 페이지 50-52, 제3.7. sfn 오류: 목표 없음: CITREFCoxeter1973(도움말)

[1]

[2]

[3]

[4]

[5]

[6]

D₄ 균일 폴리초라


{3,3^1,1} h{4,3,3}	2r{3,3^1,1} h₃{4,3,3}	t{3,3^1,1} h₂{4,3,3}	2t{3,3^1,1} h_2,3{4,3,3}	r{3,3^1,1} {3^1,1,1}={3,4,3}	rr{3,3^1,1} r{3^1,1,1}=r{3,4,3}	tr{3,3^1,1} t{3^1,1,1}=t{3,4,3}	sr{3,3^1,1} s{3^1,1,1}=s{3,4,3}

24-셀 계열 폴리토페스
이름	24셀	잘린 24셀	24셀을 훔치다	정류 24세포	24세포로 알 수 있는	24구경.	캔트런 24셀	윤택 24셀	24구경.	전지 24셀
슐레플리 심볼	{3,4,3}	t_0,1{3,4,3} t{3,4,3}	s{3,4,3}	t₁{3,4,3} r{3,4,3}	t_0,2{3,4,3} rr{3,4,3}	t_1,2{3,4,3} 2t{3,4,3}	t_0,1,2{3,4,3} tr{3,4,3}	t_0,3{3,4,3}	t_0,1,3{3,4,3}	t_0,1,2,3{3,4,3}
콕시터 도표를 만들다
슐레겔 도표를 만들다
F₄
B₄
B₃(a)
B₃(b)
B₂

Search