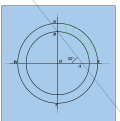
수평 다이얼에 Schema
Schema for horizontal dials수평 다이얼의 스키마는 나침반과 스트레이트 건설 기술을 사용하여 수평 해시계를 만드는 데 사용되는 일련의 명령으로, 15세기 후반부터 19세기 후반까지 유럽에서 널리 사용되었다.일반적인 수평 해시계는 적도 해시계를 수평면에 기하학적으로 투영한 것이다.
극지점 그노몬(축 그노몬)의 특수성은 13세기[1] 초 무어의 천문학자 압둘 하산 알리에 의해 처음 알려졌고, 이것은 우리에게 익숙한 문자판, 문체와 시간선이 공통의 뿌리를 가진 문자판으로 이어졌다.
수세기 동안 장인들은 익숙한 방법을 사용하여 시간대에 다른 방법을 사용하여 해시계를 표시해왔고, 게다가 이 주제는 수학자들을 매료시켜 연구 주제가 되었다.그래픽 투영법은 한때 널리 알려졌지만, 이는 삼각법, 로그, 슬라이더룰 및 산술 계산을 점점 더 하찮게 만드는 컴퓨터로 대체되었다/그래픽 투영법은 한때 해시계를 배치하는 주요 방법이었지만 지금은 학계의 관심사만 되고 있다.
그래픽 투영을 위한 스키마를 설명하는 영어로 알려진 최초의 문서는 1440년 스코틀랜드에서 출판되었고, 그 당시 목표 위도와 건설 방법에 맞는 특징을 가진 수평 다이얼을 위한 일련의 구별된 스키마를 만들었다.
맥락
해시계 설계의 기술은 현지 시간을 정확하게 표시하는 다이얼을 만드는 것입니다.해시계 디자이너들은 또한 다이얼의 계산과 정보를 표시하는 가능한 새로운 방법에 매료되었다.현대의 다이얼은 10세기에 아랍 천문학자들이 지구의 축에 평행한 그노몬이 1년 중 어느 날에나 동일한 시간 또는 법정 시간을 나타내는 해시계를 생산할 것이라는 위대한 발견을 하면서 시작되었다: 다마스쿠스에 있는 우마이야드 사원에 있는 이븐 알 샤티르의 다이얼은 이 타입의 다이얼 중 가장 오래된 다이얼이다.[a] 이 타입의 다이얼은 1440년대에 [2]오스트리아와 독일에서 등장했습니다.
1년 중 하루 종일 일정한 간격으로 그림자를 관찰하고 마킹하는 실용적 접근법에 의해 다이얼 플레이트를 배치할 수 있다.위도를 알 수 있는 경우, 다이얼 플레이트는 투영 기하학에 의존하는 기하학적 구성 기술을 사용하거나, 일반적으로 로그나 슬라이드 규칙 또는 최근 컴퓨터나 휴대 전화를 사용하여 알려진 공식과 삼각표를 사용하여 계산할 수 있습니다.선형대수는 변환을 설명하는 데 유용한 언어를 제공해 왔다.
해시계 스키마는 나침반과 직선 가장자리를 사용하여 먼저 해당 위도에 대한 필수 각도를 도출한 다음 이를 사용하여 다이얼 플레이트에 시간선을 그립니다.In modern terminology this would mean that graphical techniques were used to derive and and from it . [b]
기본계산
- 큰 종이를 사용하다.
- 맨 아래에서 시작하여 수평선이 그려지고 중앙에서 수직선이 그려집니다.그들이 교차하는 곳이 그노몬의 발원지 O가 된다.
- 수평선은 다이얼의 크기를 고정하는 선을 그립니다.중심선과 교차하는 지점이 중요한 시공 지점 F
- 시공선은 위도 [c]각도로 O에서 위쪽으로 그려진다.
- 정사각형을 사용하여 F에서 시공선을 통과하는 선을 직각으로 그립니다.그 지점 E는 중요한 건설 지점이다.정확히 말하면 sin 이므로 중요한 것은 라인 FE입니다.
- 나침반을 사용하거나 길이를 나눈 FE를 F에서 중심선 위쪽으로 복사했다.새로운 시공 지점은 G라고 불리며 시공 라인과 FE가 지워집니다.
이러한 기하학적 구조는 잘 알려져 1970년대 [3]뉴매스 혁명이 일어나기 전까지 고등학교(영국 문법학교) 교육과정의 일부로 남아있었다.
위에 나온 스키마는 1525년 (이전 작품 1440년)에 뒤러가 사용한 것으로 오늘날에도 사용되고 있다.단순한 스키마는 저위도를 위해 설계된 다이얼에 더 적합했고, 건축을 위해 좁은 종이가 필요했습니다.이것은 다른 건축물에 대한 탐구를 자극했다.
수평 다이얼
프로세스의 첫 번째 부분은 많은 방법에 공통적입니다.그것은 남북선에 자오선에서 죄악 from인 점을 설정한다.
초기 스코틀랜드 방법(1440) 뒤러(1525) 로르(1965)
- 위에 표시된 기본 방법부터 시작합니다.
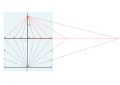
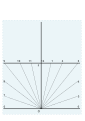
- G에서 15° 간격으로 일련의 선이 그려지며, F를 통과하는 선과 교차할 수 있을 만큼 길다.시점의 1, 2, 3 4, 5, 7, 8, 9, 10, 11이 표시됩니다.
- 다이얼의 중앙은 맨 아래 지점 O에 있습니다.이들 각 시각에서O까지의 선은 종료된 [4]다이얼의 시간선이 됩니다.
중요한 문제는 고위도에 필요한 종이의 폭이다.[5]
베네데티(1574)
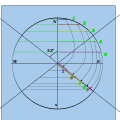
가난한 귀족인 베네데티는 사볼라의 궁정에서 수학자로 일했다.이 방법을 설명한 그의 책은 1574년에 출판된 'De gnomonum umbrarumque solarium usu'이다.이것은 오늘날 우리가 사용하는 것과 같은 법정 시간을 표시하는 방법을 설명하고 있지만, 대부분의 사람들은 여전히 낮 시간을 12시간으로 나누는 불평등한 시간을 사용하고 있지만, 해가 지남에 따라 시간이 바뀔 것입니다.베네데티스 방법은 사분면을 15° 세그먼트로 나눈다.tan h 거리를 정의하는 평행 수평선과 sin θ를 나타내는 gnomonic 극선 GT의 2가지 구성으로 한다.
- 15° 세그먼트가 있는 사분면 GRB를 그립니다.GR은 수평입니다.
- PE에서 평행한 수평선을 그리고 15°의 광선을 양분하는 곳에 진드기를 만든다.
- GX는 위도입니다.T는 PE와의 교차점이고 GTE는 Gnomonic 삼각형입니다.
- 길이 GT는 점 F를 제공하는 E의 맨 아래에 복사됩니다.
- 시간 행은 F에서 추출되어 다이얼이 완성됩니다.
베네데티는 불평등한 시간을 표시할 수 있도록 점 그노몬을 그리는 지침을 포함했다.[6]
클라비우스법 (1586)
(Fabica et us instrumenti ad horogiorum descriptionem)로마, 이탈리.
Clavius 메서드는 다이얼의 4분의 1을 조사합니다.두 다이얼의 상단 모서리에 경첩이 연결된 두 개의 직사각형으로 극축에 대한 수평 및 수직 평면을 봅니다.극축은 극축에 대해 µ도가 되며, 시간 선은 극평면에서 적도 다이얼(15°)과 같은 위치에 놓인다.극성 평면의 시간 지점은 수평 평면의 일치 지점으로 연결됩니다.수평 시간 선은 원점에 표시됩니다.
- 그 빗변 위에 누운 채 게놈 삼각형을 그립니다.
- 작은 면에는 15° 시간 표시가 있는 정사각형을 그립니다.
- 다이얼 플레이트는 삼각형을 기준으로 한 나침반으로 구성되어 있습니다.
- 시각 12, 3, 6이 알려져 있습니다.시간선 1과 2는 광장의 측면에서 가져온다.
- 대각선은 12에서 6으로, 여기에 평행한 선은 1과 2를 통해 그려지며, 5와 4를 나타낸다.
- 아침 다이얼은 이를 반영하고 있습니다.
등자법(1652)
- G에서 15° 간격으로 일련의 선이 그려지며, F를 통과하는 선과 교차할 수 있을 만큼 길다.이것들은 시점의 9, 10, 11, 12, 1, 2, 3을 표시합니다.
- 다이얼의 중앙은 맨 아래 지점 O에 있습니다.이들 각 시각에서O까지의 선은 종료된 다이얼의 시간선이 됩니다.
베티니법(1660)
예수회 마리오 베티니는 레크리에이션럼 매스매티칼럼 아피아 노비시마 1660에 사후에 출판된 방법을 썼다.
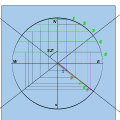
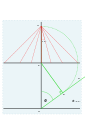
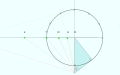
- 자오선에 대해 빗변으로 삼각형을 그리고 아래쪽에 θ를 C로 그립니다.다른 쪽 포인트는 M, 직각 콜은 G입니다.
- M을 통해 수평선이 그려지고 이것이 분점입니다.
- 반지름 MG를 가진 M을 중심으로 한 원을 그린다.G2와 G3는 원과 자오선의 교차점이다.
- 상위 사분원에는 각 30°마다 포인트가 표시됩니다.2개의 이름은 P, Q입니다.
- 건설 라인은 G2와 G3에서 P를 거쳐 그려지며, Q-는 분점과의 교차점을 표시한다.
- 시간대를 종료하려면 , C 로부터 이러한 포인트를 통과해, 다이얼은 사각형으로 표시됩니다.
- 베티니의 방법 1660
레이본 (1669년)
윌리엄 레이본은 1669년에 6단계 방식으로 그의 "다이얼링 [d]기술"을 출판했다.그의 묘사는 현의 용어선에 크게 의존하는데, 현대의 다이어리스트가 이를 견인기로 대체한다.코드 라인은 칸막이 또는 나침반 세트와 함께 사용된 섹터에서 발견된 척도입니다.그것은 [e]19세기 말까지 항해자들에 의해 여전히 사용되었다.
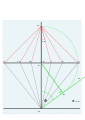
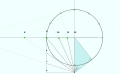
- 원과 그 두 개의 기본 직경인 E–W와 S–N(위에서 아래로)을 그립니다.O는 교차점 또는 원점입니다.
- 코드 스케일 또는 프로젝터를 사용하여 OS에서 52°인 "0a"와 OW에서 52°인 "0b" 두 줄을 바꿉니다(직각)."a"와 "b"는 중요합니다.
- E와 "a"를 연결하는 직선 가장자리를 그리면 세계의 극이라고 불리는 P에서 SN(자오선)을 절단합니다.이제 E를 "a"에 연결하면 AE가 연결됩니다.이 점은 자오선이 분점원과 교차하는 지점이기 때문에 중요하다.E, AE, W점은 분점 원에 있습니다.다음 과제는 이 정보를 사용하여 중심을 찾고 원을 그리는 것입니다.시공 라인을 사용하여 AE와 W를 결합합니다.중앙점에서 직각으로 선을 올리십시오.SN(자오선)을 절단하는 곳은 분점 원의 중심인 C가 됩니다.C를 사용하여 E에서 W로 호를 그리면 AE를 통과합니다.
- 이제 E와 W를 통과하는 반원이 있고 E와 W를 통과하는 분점 호가 있습니다. 반원을 12개의 동일한 부분, 즉 15° 각도로 나눕니다."시공 지점"으로 표시합니다.[f]
- 눈금자는 O와 반원상의 점을 결합한다.이러한 선은 분점 호를 잘라냅니다. 일련의 동일하지 않은 점("마커")이 생성됩니다.
- P(세계의 극)의 눈금자는 이 표시에서 반원 위로 선을 긋습니다.자른 곳은 "시간 지점"이 됩니다. 이 시간 지점들은 간격이 일정하지 않습니다.
- 시간 선은 이러한 각 "시점"에서 원점 O까지 그려집니다.52°로 자른 스타일의 발이 원조입니다.[10][5]
오자남의 방법(1673) Mayall(1938)
이 방법에는 훨씬 더 작은 [5]종이가 필요하며, 이는 고위도에 매우 유용합니다.
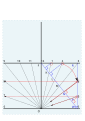
- G에서 15° 간격으로 일련의 선이 그려지며, F를 통과하는 선과 교차할 수 있을 만큼 길다.이것들은 시점의 9, 10, 11, 12, 1, 2, 3을 표시하고, h sin ( \ \h \ \ )을 .
- 다이얼의 중앙은 맨 아래 지점 O에 있습니다.이들 각 시각에서O까지의 선은 종료된 [4]다이얼의 시간선이 됩니다.
- 9와 3을 통과하는 선은 WE 선까지 연장되고 9와 3에서 WE 선까지 직교로 떨어진 선은 교차점 W'와 E'라고 합니다.W와 E에서 15° 간격으로 2개의 선이 그려집니다.이것에 의해, 시간 포인트 7, 8, 4, 5가 작성됩니다.0 에서 이들 시간 포인트로의 행이 마지막 다이얼의 시간 행입니다.
백과사전 방법(1771)
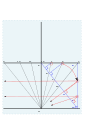
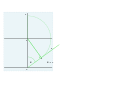
이 방법에서는 코드 속성을 사용하여 m . sin ( \ ) 。를 상단 사분면에 배치한 후 이 거리를 하단 사분면에 배치하여 sin \sin \theta 를 설정합니다.다시, 이 측정치를 상단 사분면에 있는 화음으로 전송합니다.마지막 라인은 tan sin cos { θ \ }= tan sin = sin display sin { displaystyle \이라는 을 확립합니다.
그런 다음 대칭을 통해 모든 사분면에 전달됩니다.브리태니커 백과사전 제1판 1771호, 제6판 1823호에[11] 사용되었다
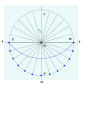
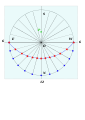
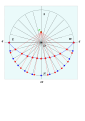
- 그노몬은 남북선을 기준으로 먼저 그려진다.그 때, 수직에 대해서 θ도의 직경을 그립니다.반사도 필요합니다.
- 원주는 상위 사분면에 15° 간격으로 표시됩니다.수평에 평행한 화음이 그려집니다(이 화음의 길이는 sin δ가 됩니다).
- 각 화음의 측정이 전송되어 하부 방사선을 따라 스케일이 형성됩니다.이 점들이 결합되면 길이가 sin θ. sin in인 일련의 평행선이 형성된다.
- 이러한 측정치는 코드까지 전송됩니다.
- 마지막 시간 선은 원점에서 이 교차점을 통해 그려집니다.( { } \ \} = sin 、 、 cos \[12]
de Celles(1760)(1790) Waugh 방식(1973년)
돔 프랑수아 베도스 드 셀레스 방법(1760) Waugh 방법(1973년)으로 알려져 있다.
- G에서 15° 간격으로 일련의 선이 그려지며, F를 통과하는 선과 교차할 수 있을 만큼 길다.3개만 취하면 시간 포인트 9, 10, 11, 12, 1, 2, 3이 표시되고 tan h sin \ \ h \ \ 가 표시됩니다.
- 다이얼의 중앙은 맨 아래 지점 O에 있습니다.이들 각 시각에서O까지의 선은 종료된 [4]다이얼의 시간선이 됩니다.
- 종이가 충분히 크면 위의 방법은 7에서 12, 12에서 5까지 작동하며 대칭을 통해 6 전후의 값을 산출한다.그러나 7과 8, 4와 5를 표시하는 다른 방법이 있습니다.3이 선 R을 교차하는 점을 호출하고 선을 기준선에 직각으로 떨어뜨립니다.그 점을 W라고 부르세요.시공 라인을 사용하여 W와 F를 연결합니다.Waugh는 K, L, M의 시간선으로 교차점을 호출합니다.
- 나침반 또는 나눗셈기를 사용하여 이 선 N과 P에 두 점을 더하여 MN = ML, MP = MK가 되도록 합니다. 누락된 시간 선은 O ~ N 및 P를 통해 그려집니다.시공 라인이 [4]지워집니다.[5]
니콜슨의 방법(1825)
이 방법은 1825년 Peter Nicholsons A의 인기 있는 순수 및 혼합 수학 과목에서 처음 등장했습니다.그것은 1903년 6월 School World에 의해 복제되었고, 그 후 Kenneth Lynch의, 해시계, Spears 1971에 복제되었다.[15] 잘 알려진 삼각형을 그리는 것으로 시작하여 정점을 사용하여 반지름(OB) sin and과 (AB) tan φ의 두 개의 원을 그립니다.이 원들과 교차하는 15° 선이 그려집니다.선은 이러한 원으로부터 수평으로, 그리고 수직으로 취해지고 교차점(OB sin t,AB cos t)은 시간선에 있습니다.그것은 sin t tan t로 분해되는 tan κ = OB sin t/ AB cos t이다.
- 원점 O에서 NS 선과 EW 선 교차를 그립니다.첫 번째 사분면의 편리한 지점에서 목표 각도로 설정된 선과 축을 결합합니다.이것이 기본 삼각 OAB를 형성합니다.
- 나침반을 OB 길이로 맞추고 원을 그립니다.AB에 나침반을 맞추고 동심원을 그리세요.이 두 원에는 모두 15°의 각도가 표시된다.
- 안쪽 원에서 수직으로, 바깥쪽 원에서 수평으로 선을 취하여 각 교차로를 표시합니다.이것들은 시간대에 있습니다.
- 교차점을 원점에 연결합니다.
Foster Serles 다이얼 스케일(1638)
- 다이얼 면에 직각을 그리고 x축에 대해 위도 스케일을 배치한다.
- 타겟의 위도 포인트는, 다이얼면의 맞은편에 표시되어 있습니다.시간 척도는 이 지점에서 정오 선까지 배치됩니다(일반적으로 영점은 정오 선 위에 있습니다).
- 각 시점은 다이얼면에 카피되어 이 순서를 반복하고, 시각은 정오 양쪽이 됩니다.직선 모서리를 사용하여 이러한 점을 원점에 연결하여 해당 위치의 시간 선을 그립니다.
- 목표 위도 지점에서 수직선과 정오 지점을 통과하는 수평선은 3시간(오전 9시–오후 3시) 마커로 이등분합니다.
- 스타일은 위도와 같은 각도로 표시됩니다.
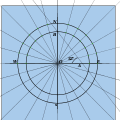
사피아 (아사피아)
이것은 만약 당신이 아스트롤라베에 접근할 수 있다면 그 시대의 많은 점성가들과 수학자들이 가지고 있었을 것처럼 사용하기 쉽고 빠른 방법이었다.이 방법은 천구의 투영을 평면 표면에 복사하는 것을 포함했다.수직선과 천구의 이등분 위에 그려진 위도의 각도에 선이 그려진 수직선이 그려졌다.[17]
「 」를 참조해 주세요.
메모들
- ^ 시간은 이탈리아 시간 또는 바빌로니아 시간으로 알려진 불평등한 시간을 사용하여 낮 시간을 12로 나누어서 측정되었다.
- ^ 영국 해시계 협회는 컴퓨터 용어와 그것들을 나타내기 위해 일반적으로 사용되는 기호들에 대한 용어집을 출판한다.Latitude는 phi,) 또는 or(또는 φ)로 표시됩니다.
- ^ 이 그림의 모든 다이얼은 52°의 위도를 사용하며, 무작위로 선택되었지만 대략 블레츨리 공원, 헤이그 또는 빌레펠트와 비슷합니다.
- ^ 다이얼링의 예술: 기하학적으로, 축척과 나침반에 의해 수행됨:산술적으로, 사인과 접선의 규범에 의해:계기적으로, 삼각기구에 의해...; 보충, 쉐잉, 스케일과 나침반에 의해 이러한 구의 원을 태양 다이얼 평면에 새기는 방법, 태양의 일주 운동을 (하루 중 시간을 제외하고) 알립니다...
- ^ 코드 [9]라인은 2015년에 건설자 금속 규칙(Stanley 60R Line of Chords Rule)에서 사용할 수 있습니다.
- ^ 60°로 설정된 코드 라인을 사용하여 분할할 수 있습니다.
레퍼런스
인용문
- ^ BSS 용어집 & 1. 오류:: (
- ^ Jones 1980, 페이지 6. 오류:: 1980
- ^ 듀렐 1921년
- ^ a b c d 와 1973, 페이지 38-39
- ^ a b c d e f g 소여 191호
- ^ 구넬라 2013b.
- ^ 구넬라 2013.
- ^ 구넬라 2014, 13페이지
- ^ "Archived copy". Archived from the original on 20 September 2015. Retrieved 11 September 2015.
{{cite web}}: CS1 maint: 제목으로 아카이브된 복사(링크) - ^ 레이본 1700년
- ^ 소여 193쪽 36쪽
- ^ 소여 193쪽 37쪽
- ^ 베도스 드 셀레스 1760, 페이지 58
- ^ 와우 1973, 페이지 38
- ^ a b 소여 194호
- ^ Sawyer, Fred (1995). "Serle's Dialing Scales". Compendium. Glastonbury, CT,USA: North American Sundial Society. 2 (2): 5.
- ^ 구넬라 2013c
원천
- Durell, Clement V (1921). Geometry. Publisher G.Bell And Sons Limited.
- Bédos de Celles, Francois (1760). "4-3". La Gnomonique pratique ou l'Art de tracer les cadrans solaires avec la plus grande précision (in French) (3 ed.). Paris. p. 459. Retrieved 12 July 2015.
- Davis, John (June 2014). "Engraved decoration English-Horizontal dials" (PDF). Bulletin. British Sundial Society. 26 (ii): 48–52. ISSN 0958-4315. Retrieved 3 July 2015.
- Rohr, René R.J. ; with a foreword by Henri Michel ; translated by Gabriel Godin (1996). Sundials : history, theory, and practice (Paperback ed.). New York: Dover Publications. pp. 142. ISBN 0-486-29139-1.
- Sawyer, Fred (1995). "Serle's Dialing Scales". Compendium. Glastonbury, CT,USA: North American Sundial Society. 2 (2): 5.
- Sawyer, Fred (2012). "Horizontal Layouts 1–4". Compendium. Glastonbury, CT,USA: North American Sundial Society. 19 (1): 33.
- Sawyer, Fred (2012). "Horizontal Layouts 6". Compendium. Glastonbury, CT,USA: North American Sundial Society. 19 (3): 36–7.
- Sawyer, Fred (2012). "Horizontal Layouts 7". Compendium. Glastonbury, CT,USA: North American Sundial Society. 19 (4): 39.
- Gunella, Alessandro (2013). Sawyer, Fred (ed.). "Horizontal Layouts 8 – Clavius Method". Compendium. Glastonbury, CT,USA: North American Sundial Society. 20 (1): 31.
- Gunella, Alessandro (2013). Sawyer, Fred (ed.). "Horizontal Layouts 9 – Benedetti Method". Compendium. Glastonbury, CT,USA: North American Sundial Society. 20 (2): 37.
- Gunella, Alessandro (2013). Sawyer, Fred (ed.). "Horizontal Layouts 10 – Saphea Method". Compendium. Glastonbury, CT,USA: North American Sundial Society. 20 (3): 39.
- Gunella, Alessandro (2013). Sawyer, Fred (ed.). "Horizontal Layouts 11 – Still a method for the Horizontal Sundial". Compendium. Glastonbury, CT,USA: North American Sundial Society. 21 (3): 13.
- Powers, Patrick (2012). Sawyer, Fred (ed.). "Horizontal Layouts 5 – Leybourns Method". Compendium. Glastonbury, CT,USA: North American Sundial Society. 19 (2): 4.
- Waugh, Albert E. (1973). Sundials : their theory and construction. New York: Dover. pp. 38–39. ISBN 0486229475.
























 수평으로.
수평으로. 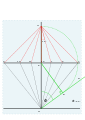














 설정합니다.다시, 이 측정치를 상단 사분면에 있는 화음으로 전송합니다.마지막 라인은 tan
설정합니다.다시, 이 측정치를 상단 사분면에 있는 화음으로 전송합니다.마지막 라인은 tan