자기 회귀 모형

이 문서에는 일반적인 참조 목록이 포함되어 있지만 대응하는 충분한 인라인 인용이 없습니다. 좀 더 정확한 인용문을 도입하여 이 기사의 개선에 도움을 주십시오. (2011년 3월) (이 템플릿메시지의 삭제 방법 및 삭제 타이밍에 대해 알아보기)

통계학, 계량경제학 및 신호처리학에서 자기회귀(AR) 모델은 랜덤 프로세스의 한 종류를 나타내는 것으로서, 자연, 경제 등의 특정 시간변화 프로세스를 기술하는 데 사용됩니다.자기 회귀 모형은 출력 변수가 자신의 이전 값과 확률적 항(불완전하게 예측 가능한 항)에 선형적으로 의존함을 명시한다. 따라서 모델은 확률적 차분 방정식(또는 미분 방정식과 혼동해서는 안 되는 반복 관계)의 형태이다.이동평균(MA) 모델과 함께, 그것은 보다 복잡한 확률 구조를 가진 시계열의 보다 일반적인 자기회귀-이동평균(ARMA) 및 자기회귀 통합 이동평균(ARIMA) 모델의 특수 케이스이자 핵심 구성요소이다. 또한 다음과 같은 벡터 자기회귀 모델(VAR)의 특수 케이스이기도 하다.둘 이상의 진화하는 랜덤 변수에서 둘 이상의 연동 확률적 차이 방정식이 있는 시스템의 ts.

이동 평균(MA) 모형과 달리 자기 회귀 모형은 단위 루트를 포함할 수 있으므로 항상 고정된 것은 아닙니다.

정의.

${\displaystyle A}$ R${\displaystyle }$(${\displaystyle p}$) {$displaystyle$ AR$(p)}$ $표기법$은 순서 p의 자기 회귀 모델을 나타냅니다.AR(p) 모델은 다음과 같이 정의됩니다.

${\displaystyle X_{t}=c+\sum _{i=1}^{p}\varphi _{i}X_{t-i}+\varepsilon _{t},}$

여기서 ${\displaystyle {1\mathrm{}}_{}}$1, ${\displaystyle ...,}$ ${\displaystyle p_{}}$ p$$\ $displaystyle$\$varphi$_ {$1},$ \$ldots$, \ $varphi$_ {$p}$는 모델의 파라미터,$c{\displaystyle }$ \ $displaystyle$$$c$$}는$$ 상수, ${\$ ${\displaystyle t_{}}$ \ $displaystyle$ \ $varepsilon$_ { $t}$는 화이트 노이즈입니다.이는 백시프트 연산자 B를 사용하여 동등하게 기술할 수 있습니다.

${\displaystyle X_{t}=c+\sum _{i=1}^{p}\varphi _{i}B^{i}X_{t}+\varepsilon _{t}$

그래서, 합계항을 왼쪽으로 이동하고 다항식 표기법을 사용하면,

$\displaystyle \phi [B]X_{t}=c+\varepsilon _{t},}$

따라서 자기 회귀 모델은 입력이 백색 노이즈인 전극 무한 임펄스 응답 필터의 출력으로 볼 수 있다.

모델이 와이드 센스 정지 상태를 유지하려면 일부 매개 변수 제약 조건이 필요합니다.예를 들어, AR(1) 모델의 프로세스가 "${\displaystyle {1\mathrm{}}_{}"{}_{}}$ "$"$ {$displaystyle \varphi _{1}$ \$geq$ 1$"$ 이면$$ 정지되어 있지 않습니다.보다 일반적으로 AR(p) 모델이 광의 정지 상태일 경우 다항식 $\delta {\displaystyle \mathrm{}(z)}$의 근은 다음과 같습니다. ${\displaystyle =1\mathrm{}}$ -${\displaystyle \underset{\delta }{\overset{}{}}}$ i ${\displaystyle \underset{}{\overset{}{=}}}$ ${\displaystyle \underset{}{\overset{}{}}}$ p ${\displaystyle {\delta }_{}}$ ${\displaystyle {}_{}{}^{}}$ i ${\displaystyle i^{}}$ i$${\$displaystyle \Phi (z):$$=\textstyle 1-\sum _{i=1}^{$p$$}\$varphi _{i}$는 단위 원 밖에 있어야 합니다. 즉, 각 (복소) ${\displaystyle {루트}_{}}$ $z$i {\$displaystyle z_{$i$$}는 z $>$ 1 {$displaystyle z_{$i} $>$1}을 해야 (페이지 89,92 참조).

충격의 일시적 영향

AR 프로세스에서 일회성 충격은 미래로 무한히 발전하는 변수의 값에 영향을 미칩니다.예를 들어 AR(1) $모델{\displaystyle {}_{}}$ X ${\displaystyle t_{}}$ ${\displaystyle {}_{}c}$ + ${\displaystyle {1\mathrm{}}_{}}$ 1 ${\displaystyle X_{}}$t -${\displaystyle {}_{}{1}_{}}$ + ${\displaystyle t_{}}$ t$${ $display style$ X _ { t } =$c$+ \ $varphi$_ {$1}$ X _ {$t-1}$ + \ $varepsilon$ _ ${ t$ $a{\displaystyle {}_{}}$ ${\displaystyle {time}_{}}$ time time {\ {\ {\ {\ {\ ${\$ t \ $display$ style \$varepsilon$ _ 1 = { $t$}} time$$ time time time time time time time time time time time time x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x다음으로 ${\displaystyle {X2}_{}}$의$AR{\displaystyle {}_{}}$ 방정식($X1$의 $경우{\displaystyle {}_{}}$ ${$$displaystyle X_$${1$에 의해 $($ {$displaystyle$ X_{$2})$에 $1{\displaystyle {}_{}}$$$ 1 \ $displaystyle$\ $varphi _ {$1} \ $varepsilon$_ {1$}$ 。${\displaystyle {다음}_{}}$으로 ${\displaystyle {X3}_{}}$의 AR방정식$($경우$)$에 $의해{\displaystyle {}_{}}$ ${\displaystyle {X3\mathrm{}}_{}}$$($$X2$의 경우)에 $영향$을 줍니다(X2의 경우$).$ 이 처리는 X3$($의 경우)에$$ $(\$1$\}\backslash$$varepsilon _1}$의 양만큼 영향을 줍니다.이 처리는 1$(\$style)을 ${\displaystyle {나타냅니다\mathrm{}}_{}}$.$_{1}}:$ 프로세스가$$ 정지되어 있으면 한계에서 효과가 0으로 감소하지만 절대 끝나지 않습니다.

각 충격은 발생 시점부터 미래까지의 X 값에 무한히 영향을 미치기 때문에 주어진 값_t X는 무한히 과거에 발생한 충격의 영향을 받습니다.이것은, 자동 복귀를 고쳐 쓰는 것으로도 확인할 수 있습니다.

$\displaystyle \phi (B)X_{t}=\varepsilon _{t},}$

(변수가 평균으로부터의 편차로 측정되었다고 가정하여 상수항이 억제된 경우)

${\displaystyle X_{t}=blac{1}{\phi(B)}}}\varepsilon_{t},}$

오른쪽 다항식 나눗셈을 실행하면 ${\displaystyle {\theta }_{}}$ t$\$${t$$}$에 적용되는 백시프트 연산자의 다항식은 무한 차수를 갖습니다. 즉, ${\displaystyle {\theta }_{}}$ t$\displaystyle\varepsilon_{$t$$}의 지연 값이 방정식 오른쪽에 무한히 표시됩니다.

특성 다항식

AR(p) 프로세스의 자기 상관 함수는 다음과 같이 표현될^{[citation needed]} 수 있습니다.

${\displaystyle \rho (\displaystyle )=\sum _{k=1}^{p}a_{k}y_{k}^{-\display}}$

${\displaystyle {여기}_{}}$서 y k$(\$는 다항식의 근입니다.

$\displaystyle \phi (B)=1-\sum _{k=1}^{p}\varphi _{k}B^{k}$

여기서 B는 백시프트 연산자입니다${\displaystyle .}여기$서 " (${\displaystyle )}$) \ $displaystyle \phi$( \$cdot$) is$$ 、 ${\displaystyle k_{}}$ k $\$ \ $varphi _$ { $k$} 、 k$$ 、 ore 、 oreoreoreoreore where where where where where where 。이 공식은 모든 루트에 다중도 ^{[citation needed]}1이 있는 경우에만 유효합니다.

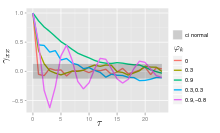
AR(p) 프로세스의 자기 상관 함수는 감소하는 지수의 합계입니다.

• 각 실근은 지수적으로 감소하는 자기 상관 함수에 성분을 제공합니다.
• 마찬가지로, 복잡한 공역근의 각 쌍은 지수 감쇠 진동을 일으킵니다.

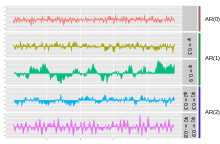
AR(p) 공정 그래프

가장 간단한 AR 공정은 항 사이에 종속성이 없는 AR(0)입니다.오차/혁신/잡음 항만 공정의 출력에 기여하므로 그림에서 AR(0)은 백색 잡음에 해당합니다.

양의 $"\displaystyle \varphi$를 가진 AR(1) 프로세스의 경우 프로세스의 이전 항과 노이즈 항만 출력에 기여합니다.${\$ { $displaystyle \ varphi }$가 0에 가까울 경우 프로세스는 여전히 백색 노이즈로 보이지만 ${\$ { \ $displaystyle$ \ $varphi$}가 1에 가까워질수록 노이즈에 비해 출력 기여도가 높아집니다.그 결과 로우패스 필터와 마찬가지로 출력이 "스무딩"되거나 통합됩니다.

AR(2) 프로세스의 경우 앞의 두 항과 노이즈 항이 출력에 기여합니다.$(\$과 $(\$ _${2})$ 모두$$ 양의 경우 출력은 로우패스필터와 비슷하며 노이즈의 고주파수가 감소합니다.${\displaystyle {1\mathrm{}}_{}}$ 1$$( \ $displaystyle$ \ $varphi$_ { $}$ )이$$$$ 양수이고 ${\displaystyle {2\mathrm{}}_{}}$2 ( \ $displaystyle$ \ $varphi _$ {$$2})이 음수인 경우 프로세스는 프로세스 조건 간의 부호 변경을 선호합니다.출력이 진동합니다.이는 에지 감지 또는 방향 변경 감지와 유사할 수 있습니다.

예제:AR(1) 프로세스

AR(1) 프로세스는 다음과 같이 제공됩니다.

${\displaystyle X_{t}=c+\varphi X_{t-1}+\varepsilon _{t},}$

${\displaystyle {여기}_{}}$서 t$$t \ $displaystyle \ varepsilon$_ { $t$}는$$ 평균이 0이고 분산이 일정한 백색 노이즈 처리입니다. ${\displaystyle {\mathrm{}}_{}^{}}$2 { \ $displaystyle$ \ $sigma$_ { \ $varepsilon$}^2}$$（ : : ） 。§ ${\displaystyle {1\mathrm{}}_{}}$(\$displaystyle \varphi _{1})$의 서브스크립트가 삭제되었습니다.입력이 백색 노이즈인 안정적인 필터의 출력으로 얻어진 \ $displaystyle$\ $varphi < 1$이면 프로세스는 광의 정지 상태입니다.($\theta {\displaystyle }$ ${\displaystyle =}$ ${\displaystyle 1}${$displaystyle \varphi =1}$인 경우 ${\displaystyle X_{}}$t {$displaystyle X_{t}}$의 분산은 시간 시차 t에 따라 달라지므로 계열의 분산은 무한대로 분산되므로 넓은 의미의 정지 상태가 아닙니다.) $<$ 1 \ $displaystyle$ \$varphi$ < 1$$ 、${\displaystyle }$\ $displaystyle \operatorname${ $E$（ X $_${ $t$） } is$$is 、 와이드 센스 정지성의 정의에 의해 t의 모든 값이 동일합니다.평균이$$μ {\$displaystyle \mu$로 $표시$될 경우 다음 값이 됩니다.

${\displaystyle \operatorname {E}(X_{t})=\operatorname {E}(c)+\varphi \operatorname {E}(X_{t-1})+\operatorname {E}(\varepsilon _{t}),}$

그거

$\displaystyle \mu = c+\varphi \mu +0,}$

그렇기 때문에

$(\displaystyle \mu = parfrac {c}{1-\varphi}}).}$

특히 c ${\displaystyle =}$ $(\displaystyle$ c$=0$인 $경우{\displaystyle }$ 평균은 0입니다.

편차는

${\displaystyle {textrm {var}(X_{t}^{2})=\operatorname {E}(X_{t})-\mu ^{2}=blac {{\varepsilon}^2}}{1-\varphi ^{2}}}},$

여기서 ${\displaystyle {\sigma }_{}}${ $display style$ \ $varepsilon }$은 ${\displaystyle t_{}}$ ${\$ t \ $display$ style \ $varepsilon$_ { $t$}의 표준 편차입니다.이것은, 다음과 같은 점에 주의하는 것으로 알 수 있습니다.

${\displaystyle {textrm {var}(X_{t})=\varphi ^{2}{\textrm {var}}(X_{t-1})+\sigma _{\varepsilon}^2}$

그리고 위의 수량이 이 관계의 안정적인 고정점이라는 것을 알게 된다.

자기변환율은 다음과 같습니다.

${\displaystyle B_{n}=\operatorname {E}(X_{t+n}X_{t})-\mu ^{2}=blac {{\varepsilon}{2}}{1-\varphi ^{2}},\varphi ^{n}}.$

자기변동함수는 붕괴시간(${\displaystyle \mathrm{시간상수}}$라고도 함)이 ${\displaystyle =}$ -${\displaystyle 1}$ / ${\displaystyle \ln }$ ${\displaystyle （}$\ $displaystyle$\ $display$=$1$/ \$$ln ( \ $varphi$ ) $$[${\displaystyle {이것}_{}}$을 확인하려면 , B n${\displaystyle {}^{}}{\displaystyle {}_{}}$ ${\displaystyle K}$ = ${\displaystyle K^{}}$ ${\displaystyle {}^{}}$ \ $display style$ B_${n$ } $=$$K$\ $var$ phi$$$^{$ display phi } 의$$ { } 로 $입력$합니다$.$Then note that ${\displaystyle \varphi ^{ n }=e^{ n \ln \varphi }}$ and match this to the exponential decay law ${\displaystyle e^{-n/\tau }}$].

스펙트럼 밀도 함수는 자기변환 함수의 푸리에 변환입니다.이산 용어로는 이것이 이산 시간 푸리에 변환입니다.

${\displaystyle \Phi(\ophicrt {2\pi }},\sum _{n=-\infty}^{\infty}B_{n}e^{-i\ophicrt {2\pi }}=\frac {1},\frcrcrcrc{{\pi } {\pi}{{{v}}}$

이 표현은 X $($분모에서 코사인 항으로 나타나는 X j(\$displaystyle X_{$j$\})$의 이산적인 성질 때문에 주기적입니다.샘플링 시간(${\displaystyle \delta }$ t ${\displaystyle =}$ \ $displaystyle$\$Delta$ t$=$ 1)이 붕괴 시간(${\displaystyle }$\ $displaystyle$\$$ $displaystyle$)보다 훨씬 작다고 가정하면 B$$ \ $displaystyle B_{n$에 $대한{\displaystyle {}_{}}$ 연속체 근사치를 사용할 수 있습니다.

${\displaystyle B(t)\약 {\frac {sigma _{\varepsilon }^{2}} {1-\varphi ^{2}},\varphi ^{t }}$

이는 스펙트럼 밀도에 대한 로렌츠 프로파일을 생성합니다.

${\displaystyle \Phi (\오메가 )=blac {1}{2\pi}}, {\frac {\varepsilon }^2}}{1-\varphi ^{2}, {\flac {\pi }(\flac ^2}+\pi)}}$

여기서 $\gamma {\displaystyle }$ ${\displaystyle =1}$ /$$ { $display style$\ display =$1$/ \ $display }$는 붕괴 시간$$frequency { $displaystyle$ \ $display$ $\}$

${\displaystyle X_{}}$ t${\displaystyle {}_{}}$- ${\displaystyle 1_{}}$({$display style$ X_${t-1})$에 $대해{\displaystyle {}_{}}$ 정의된 식에서 먼저${\displaystyle }$c + ${\displaystyle t_{}{}_{}}$X ${\displaystyle {\mathrm{t}}_{}}$- ${\displaystyle {}_{}}$ + ${\displaystyle {-}_{}}$ ${\displaystyle {\mathrm{t}}_{}}$- 1 (\$display$c+\$varphi X_{$t-2$}+\varepsilon _$${$t-1$$})로 치환하여 X$$t의 대체식을 도출할 수 있습니다.이 프로세스를 계속하면 수율이 N배로 증가합니다.

${\displaystyle X_{t}=c\sum _{k=0}^{N-1}\varphi^{k}+\varphi^{n}X_{t-N}+\sum _{k=0}^{N-1}\varphi^{k}\varepsilon_{t-k}.}$

무한대에 가까워지는 N의 경우 ${\displaystyle {\theta }^{}}$ N$(\$^{$N})$은 0에 가까워지고 다음과 같이 됩니다.

${\displaystyle X_{t}=varfrac {c}{1-\varphi }}+\sum _{k=0}^{\infty}\varphi ^{k}\varepsilon _{t-k}.}$

${\displaystyle X_{}}$ t$${ $style X$_ { $t$} ${\displaystyle k^{}}$ k$$\$display$ \ $varphi$^ { $k$} 커널에$$ 상수 평균을 더한 백색 노이즈인 $것$을 알 수 있습니다.백색 ${\displaystyle {노이즈\theta }_{}}$ t$${\$displaystyle \varepsilon$ _${t}}$이 가우스 프로세스인 $경우{\displaystyle {}_{}}$ ${\displaystyle X_{}}$ t$${\$displaystyle X_{$t}도$$ 가우스 프로세스입니다.$다른{\displaystyle }$ 경우 중심 한계 정리에 따르면$$${\displaystyle {\delta }_{}}${\$displaystyle \varphi }$이(가) 1에 가까울 때 X t {\$displaystyle$ X_${t}}$이(가) 거의 정규 분포를 $따릅니다{\displaystyle {}_{}}$.

c ${\displaystyle =}$ ${\displaystyle t_{}}$ t ${\displaystyle {}_{}}$ { $displaystyle$ c = \ $varepsilon$_ { t } = $0$} 의 $경우{\displaystyle }$ $프로세스{\displaystyle {}_{}}$ ${\displaystyle X_{}}$ t ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ X${\displaystyle t_{}}$ -$$ { $displaystyle$ X_${t$ }= \ $varphi$X_{$t-1$$}$ 은 기하급수(지속적 성장 또는 붕괴)가 됩니다.$이{\displaystyle {}_{}}$ 경우 X ${\displaystyle t_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle a^{}}$ ${\displaystyle {}^{}}$ { $displaystyle X_${t =$$a \ $varphi$^ { t$$$$} （ \ $displaystyle$ a } $）$ 。$여기$서 { $displaystyle$ a$}$는 알 수 없는 상수(초기 조건)이다.

AR(1) 프로세스의 명시적 평균/차이 형식

AR(1) 모델은 연속적인 Ornstein-Uhlenbeck 과정의 이산 시간 유사입니다.따라서 동등한 형태로 주조된 AR(1) 모델의 특성을 이해하는 것이 유용할 수 있습니다.이 형식에서 프로세스 $파라미터$가$$\$displaystyle \theta$인 AR(1) 모델은 다음과 같이 표시됩니다.

$X$t + ${\displaystyle 1_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}{t}_{}}$+ (${\displaystyle 1}$ - ${\displaystyle )}$) (${\displaystyle \mu }$ - $X$t${\displaystyle }$) + ${\displaystyle {\mu }_{}}$t +$$ ( \ $display$ $style$ X $_$ ${ t$ + $1$）$$$= X$ _ { $t }$ + \ $epsilon _$${ t$+$1$$$μstyle $）$

이것을 X ${\displaystyle t_{}}$+ ${\displaystyle 1_{}}$ $=$ + ${\displaystyle {}_{}}$ ${\displaystyle X_{}{}_{}}$t + x X t + $t$ t${\displaystyle {}_{}}$+$$ { $display X _$ {$t$ + \ $phi X$$_$ { $t }$ \ + \ $explon$ _ {$$$t$ + $n$} 의 $형식$으로 하고, X${\displaystyle t_{}}$ + ${\displaystyle n_{}}$의 $시리즈$를 전개하면, 다음과 같이 할 수 있습니다.

${\displaystyle \mathrm{E}(}$ ( ${\displaystyle {}_t}$ + ${\displaystyle n_{}}$ ${\displaystyle X{}_{}{}_{}{t}_{}}$ ) ${\displaystyle =\mu }$ [${\displaystyle 1\mathrm{}}$ - ${\displaystyle n^{}}$ n${\displaystyle {}^{}]}$ + X ${\displaystyle t_{}}$ ${\displaystyle n^{}}$n \ $displaystyle \operatorname${$E$} ( X$_$ { $t$} $X$_ { t } = \$mu$ \$left$ [ 1 - \ $theta ^$ { $n$} \ $t$} \ ta ^ { $n$} } } 、

${\displaystyle {Var}_{}}$ "${\displaystyle }$( ${\displaystyle {}_{}}$ t${\displaystyle {}_{}}$+ ${\displaystyle n_{}}$ ${\displaystyle X{}_{}{}_{}{t}_{}}$ ) ${\displaystyle =}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\displaystyle {}^{}\frac{\mathrm{}}{}}$ - ${\displaystyle \frac{{2\mathrm{}}^{}}{{}^{}}}$ \ displaystyle $\operatorname { Var$}($X_{t} X_{t$})=\$sigma$^{2$}{\frac {1-\theta ^2n}$ {$1-\ta ^2}}$$=$

최대 지연 선택

그래서 적절한 최대 지연은 초월한 부분 autocorrelations a AR(p)과정의 파코어는 p[해명 필요한]의 주문보다 크지 않다 지연에 및 X1{\displaystyle X_{1}사이의 상관 관계 좋은 모델을 제공합니다}및 Xp+1{\displaystyle X_{p+1}}, 0와 같모두 0을 보강하다.

AR 파라미터의 계산

일반적인 최소 제곱 절차 또는 모멘트 방법(율-워커 방정식을 통해)과 같이 계수를 추정하는 방법은 여러 가지가 있습니다.

AR(p) 모델은 다음 방정식으로 주어진다.

${\displaystyle X_{t}=\sum _{i=1}^{p}\varphi _{i}X_{t-i}+\varepsilon _{t},$

파라미터 ${\displaystyle i_{}}$i { \ $displaystyle$\$varphi _$ { $i$} (i$$ = 1, ..., p )에 근거하고 있습니다.이 파라미터와 프로세스의 공분산함수 사이에는 직접적인 상관관계가 있으며, 이 대응관계를 반전시켜 자기상관함수(공분산함수로부터 취득)로부터 파라미터를 결정할 수 있습니다.이것은 Yule-Walker 방정식을 사용하여 수행됩니다.

율-워커 방정식

Udny Yule과 Gilbert ^[2][3]Walker의 이름을 딴 Yule-Walker 방정식은 다음과 같은 일련의 ^[4]방정식입니다.

$\displaystyle _{m}=\sum _{k=1}^{p}\varphi _{k}\varepsilon _{m-k}+\display_{\varepsilon }^{2}\display_{m,0}$

여기서 m = 0, …, p, p + 1 방정식을 산출합니다.여기서 ${\displaystyle m_{}}$ m$$\ $displaystyle$ \ $gamma$_ { $m$}는$$ X의_t 자기변수 함수이며,$σ$ m , 0 \ $displaystyle$ \ $sigma$ _ { \ $varepsilon }$은 입력 노이즈 프로세스의 표준 편차이며, ${\displaystyle m_{}}$ m${\displaystyle {}_{}}$, ${\displaystyle 0_{}}$ \ displaystyle \ $delta$_ {$m$ , $0$}은$$ 크로네커 델타 함수입니다.

개별 방정식의 마지막 부분은 m = 0일 때만 0이 아니기 때문에, 방정식 집합은 m > 0에 대한 방정식을 행렬 형태로 표현함으로써 풀 수 있다.

${\displaystyle{\begin{bmatrix}\gamma _{1}\\\gamma _{2}\\\gamma _{3}\\\vdots \\\gamma _{p}\\\end{bmatrix}}={\begin{bmatrix}\gamma _{0}&, \gamma _{)}&, \gamma _{-2}&, \cdots \\\gamma _{1}&, \gamma _{0}&, \gamma _{)}&, \cdots \\\gamma _{2}&, \gamma _{1}&, \gamma _{0}&, \cdots \\\vdots, \vdots &, \vdots & &, \ddots \\\gamma다.{p-1}&, \gamma _{p-2}&, \gamma _{p-3}&, \cdots \\\end{bmatrix}}{\varphi_{1}\\varphi_{2}\varphi_{3}\vdots\varphi_{p}\\end{bmatrix}}}$

이는 모든${\displaystyle }${${\displaystyle {\mu m}_{}}$; ${\displaystyle m}$ ${\displaystyle =1}$,${\displaystyle 2}$,${\displaystyle \dots ,}$ ${\displaystyle p}$ ${\displaystyle \}}$ .$${$displaystyle \{\varphi$ _${m};m=1,2,\display,p\}$에 대해 풀 수 있습니다. m = 0에 대한 나머지 방정식은 다음과 같습니다.

${\displaystyle _{0}=\sum _{k=1}^{p}\varphi _{k}\display_{-k}+\display_{\varepsilon }^2}$

{ , ${\displaystyle m_{}}$; ${\displaystyle m}$ ${\displaystyle =1}$,${\displaystyle 2}$, …${\displaystyle }$} , ${\displaystyle p}$ $}$ { $displaystyle$\ { \ $varphi$_ { $m$} ; m$= 1$, 2, \ display ,$$p \ } 이$$ 확인되면 ${\displaystyle }$${\displaystyle {}_{}^{}}$2 .$${ \ $displaystyle \$ { \ $varepsilon }^2$} 에 대해 해결할 수 있습니다.$}$

다른 공식은 자기 상관 함수에 관한 것입니다.AR 파라미터는 자기상관함수의 첫 번째 p+1 요소 ${\displaystyle (}$ ($$\ $displaystyle \rho$( \ $tau$)에 의해 결정됩니다.그런 다음 완전 자기 상관 함수는 재귀적으로 계산하여 도출할 수 있다.

$\displaystyle \rho (\displaystyle )=\sum _{k=1}^{p}\varphi _{k}\rho (k-\display)}$

일부 하위 AR(p) 프로세스의 예

• p=1
  • $\displaystyle _{1}=\varphi _{1}\displaystyle _{0}$
  • 따라서 ${\displaystyle {1\mathrm{}}_{}}$ 1 ${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$1 / ${\displaystyle {0\mathrm{}}_{}}$ 0 ${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$1 { $displaystyle \rho$_ {1} = \ $displaystyle$_ {1} / \$displaystyle$_ { 0 } = \ $varphi _ {1$}
• p=2
  • AR(2) 프로세스의 Yule-Walker 방정식은 다음과 같습니다.

    $\displaystyle _{1}=\varphi _{1}\varphi _{0}+\varphi _{2}\varphi _{-1}$

    $\displaystyle _{2}=\varphi _{1}\varphi _{1}+\varphi _{2}\varphi _{0}$

    • ${\displaystyle {"}_{}}$ - ${\displaystyle k_{}}$ ${\displaystyle {}_{}}$ "$$ \ $displaystyle$ \$displaystyle _${ - k } = \ $displays _${ k } 。
    • 첫 번째 방정식을 사용하면 ${\displaystyle {1\mathrm{}}_{}}$ 1 ${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$1 / ${\displaystyle {0\mathrm{}}_{}}$ 0 ${\displaystyle {}_{}}$ ${\displaystyle \frac{{1\mathrm{}}_{}}{}}$ ${\displaystyle \frac{{}_{}}{\mathrm{}}}$- 2$$1 - ${\displaystyle \frac{{2\mathrm{}}_{}}{}}$ 2 { display $style \rho$_ {1} / \ $display$_ { 0 }$= fr frac$ { $1$- \ $varphi$ _ { $} }$ } 。
    • 재귀 수식을 사용하면 ${\displaystyle {2\mathrm{}}_{}}$ 2 ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ 2 / ${\displaystyle {0\mathrm{}}_{}}$ 0 ${\displaystyle {}_{}}$ ${\displaystyle \frac{{\mathrm{}}_{}^{}}{}}$ 1${\displaystyle \frac{{}_{}^{}}{}}$2 - ${\displaystyle \frac{{}_{}^{}}{}}$2 2 + ${\displaystyle \frac{{}_{}}{\mathrm{}}}$ 2${\displaystyle \frac{}{}}$1 -$$ 2 \ $displaystyle \rho$_ { 2$$= \ $display$ frac _ { 2 } / \ $rho$_ { 0 }$=$ { { { 0$fr$ frac \ $varphi$_ { { }^{ } - { { { { { } - $2 }$ } { $var phi$ } _ { var phi _ { { $var phi$ } } _ { var $phi$

AR 파라미터의 추정

위의 방정식(율-워커 방정식)은 이론 공분산을 추정값으로 ^[6]대체함으로써 AR(p) 모델의 파라미터를 추정하기 위한 몇 가지 경로를 제공합니다.이러한 변형 중 일부는 다음과 같이 설명할 수 있습니다.

• 자기 분산 또는 자기 상관의 추정입니다.여기서는 각 항을 기존 추정치를 사용하여 별도로 추정합니다.이를 수행하는 방법은 다양하며, 이들 중 하나를 선택하는 것은 추정 체계의 속성에 영향을 미칩니다.예를 들어, 일부 선택에 의해 분산의 음수 추정치가 생성될 수 있습니다.
• 정규 최소 제곱 예측 문제가 구성되는 최소 제곱 회귀 문제로 공식화되며, 동일한 계열의 p 이전 값을 기준으로_t X 값을 예측합니다.이것은, 예측 스킴이라고 생각할 수 있습니다.이 문제에 대한 정규 방정식은 동일한 지연의 자기변환의 각 외관이 약간 다른 추정치로 대체되는 Yule-Walker 방정식의 행렬 형식의 근사치에 해당하는 것으로 볼 수 있다.
• 일반 최소 제곱 예측 문제의 확장된 형태로 공식화.여기서 두 세트의 예측 방정식이 단일 추정 체계와 단일 세트의 정규 방정식으로 결합됩니다.한 세트는 AR 모델의 역방향 표현과 관련된 역방향 예측 방정식의 세트이고 다른 한 세트는 해당 역방향 예측 방정식의 세트입니다.

${\displaystyle X_{t}=c+\sum _{i=1}^{p}\varphi _{i}X_{t-i}+\varepsilon _{t}^*},}$

여기서 X의 예측_t 값은 동일한 ^{[clarification needed]}계열의 p 미래 값을 기반으로 합니다.이 AR 파라미터의 추정방법은 ^[7]Burg에 의한 것으로 Burg ^[8]메서드라고 불립니다.Burg와 그 이후의 저자들은 이러한 추정치를 "최대 엔트로피 추정치"^[9]라고 불렀지만, 이 배경의 논리는 추정된 AR 모수의 사용에 적용된다.순방향 예측 방정식만 사용하는 추정 체계와 비교하여 자기 이동의 다른 추정치가 생성되고 추정치의 안정성 특성이 다릅니다.버그 추정치는 특히 최대 엔트로피 스펙트럼 ^[10]추정과 관련이 있다.

추정할 수 있는 다른 방법으로는 최대우도 추정이 있습니다.두 가지 뚜렷한 최대우도 변형을 사용할 수 있다. 하나의 (전진 예측 최소 제곱 체계와 광범위하게 동일) 우도 함수는 계열의 초기 p 값이 주어진 계열의 이후 값의 조건부 분포에 대응하는 것이다. 두 번째에서, 고려된 우도 함수는 t이다.관측된 시계열에서 모든 값의 무조건 결합 분포에 해당하는 모자.관측된 연속이 짧거나 공정이 비정상성에 가까운 경우 이러한 접근법의 결과에 상당한 차이가 발생할 수 있다.

스펙트럼

$잡음{\displaystyle \mathrm{}}$ ${\displaystyle \mathrm{분산}}$ V a ${\displaystyle {}_{}}$(${\displaystyle {}_{}}$Z t ) ${\displaystyle =}$ ${\displaystyle {\mathrm{}}_{}^{}}$ ${\displaystyle Z_{}}$2 ( \ $displaystyle \ mathrm$ {$Var$} ( Z _ { t ) = \ $sigma _$ { Z }^$2}$인^[5] AR(p) 프로세스의 PSD는 다음과 같습니다.

$({displaystyle S(f)=parfrac {\sum _{k=1}^{p}\varphi _{k}e^{-i2\pi fk}^{2}}).}$

AR(0)

백색 소음의 경우(AR(0))

${\displaystyle S(f)=\sigma _{Z}^{2}.}$

AR(1)

AR(1)의 경우

${{displaystyle S(f)=varfrac {{Z}^{2}}{ 1-\varphi _{1}e^{-2\pi if}^{2}=varfrac {1+\varphi _{1}^{1}-2\cos\pi}f}f}$

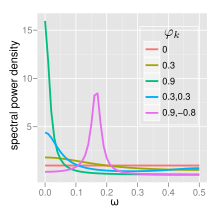
• 1> { $displaystyle \varphi _{1}$ > $0$}인 경우 f=0에서 단일 스펙트럼 피크가 존재하며, 종종 빨간색 노이즈라고 합니다.§ $($ 스타일 $\varphi$ _${1})$이 1에 가까워질수록 저주파수, 즉 더 큰 시간 지연으로 더 강력한 전력이 공급됩니다.이것은 저역 통과 필터이며, 풀 스펙트럼 빛에 적용하면 빨간색 빛을 제외한 모든 것이 필터링됩니다.
• 1 < \ $displaystyle \varphi _{1}<0}$인 경우, f=0의 최소값이 존재하며, 흔히 블루 노이즈라고 합니다.이것은 마찬가지로 하이패스 필터로서 기능하며, 파란색 빛을 제외한 모든 것이 필터링됩니다.

AR(2)

AR(2) 프로세스는 루트의 특성에 따라 다음 3개의 그룹으로 나눌 수 있습니다.

${\displaystyle z_{1},z_{2}=-{\frac {1}{{2}\left(\varphi_{1}\pm {{pm}rt {{1}^{2}+4\varphi_{2}}\right}$

• 1 + 2< \ $displaystyle$\$varphi$_ { $1$}^{$2}$ + $4$\ $varphi$_ {2} <$0$의 경우, 이 프로세스에는 복소 공역 루트 쌍이 있으며, 다음과 같은 중주파 피크가 생성됩니다.

${\displaystyle f^{*}=cos frac {1}{-1}\cos ^{-1}\frac {varphi _{2}-1}{4\varphi _{2}}\right}$

그렇지 않으면 프로세스는 실제 뿌리를 가지고 있습니다.

• 1> { $displaystyle$\ $varphi$_ {1$}$ > $0$} 이면 f $=$ { $displaystyle$ f $=$0 } 의 $스펙트럼{\displaystyle }$ 피크로 백색 노이즈에 대한 로우패스 필터 역할을 합니다.
• 1< { $displaystyle$\$varphi _$ { $1 }$ < 0 } $acts$ 、 ${\displaystyle \mathrm{f}}$ ${\displaystyle =}$/ 2 ( \ $displaystyle$ f $= 1/$2 $)$의 스펙트럼 피크로 백색 노이즈에 대한 하이패스 필터 역할을 합니다.

루트가 단위 원 밖에 있는 경우 프로세스는 비정상입니다.루트가 단위 원 안에 있을 때 또는 계수가 삼각형 $-{\displaystyle }$ 1${\displaystyle 1}$ 2${\displaystyle {}_{}1}$1 - ${\displaystyle {1\mathrm{}}_{}{}_{}}$1 { $displaystyle$ - 1 \$leq \varphi$ _${2}$ \$leq 1- \varphi$ _{$1$}에 $있을$ 때 프로세스는 안정적입니다$.$

완전한 PSD 함수는 다음과 같이 실제 형태로 표현할 수 있습니다.

${\displaystyle S(f)=varfrac {{Z}{1+\varphi _{1}^2}+\varphi _{2}-2\varphi _{1}(1-\varphi _{2})\cos(2\pi f)-2\varphi _{2\cos4} f}$

통계 패키지 구현

• R, stats 패키지에는 ar ^[11]함수가 포함되어 있습니다.
• MATLAB의 Econometrics^[12] Toolbox 및 System Identification^[13] Toolbox에는 자기 회귀 모델이^[14] 포함되어 있습니다.
• Matlab 및 Octab: TSA 도구 상자에는 단변수,^[15] 다변량 및 적응형 자기 회귀 모형에 대한 여러 추정 함수가 포함되어 있습니다.
• PyMC3: 베이지안 통계 및 확률론적 프로그래밍 프레임워크는 p 지연이 있는 자기 회귀 모드를 지원한다.
• bayesloop은 AR-1 프로세스에 대한 파라미터 추론 및 모델 선택을 지원합니다.^[16]
• Python: statsmodel에서의 ^[17]구현.

임펄스 응답

시스템의 임펄스 응답은 k의 함수로써 이전의 충격 항 k의 값의 변화에 대한 반응으로 진화하는 변수의 변화이다.AR 모델은 벡터 자기회귀 모델의 특수한 경우이기 때문에 벡터 자기회귀 #임펄스 응답에서의 임펄스 응답 계산이 여기에 적용됩니다.

n단계 예측

일단 자동 복귀의 매개 변수가 되면

${\displaystyle X_{t}=c+\sum _{i=1}^{p}\varphi _{i}X_{t-i}+\varepsilon _{t},}$

추정된 경우, 자동 복귀를 사용하여 미래의 임의의 수의 기간을 예측할 수 있습니다.첫번째 사용하지 않는 데이터는 아직 사용할 수 없는 경우 첫번째 기간을 언급할 때,ε t{\displaystyle \varepsilon_{t}}0과 같은 오류 기간 설정 Xt-i i=1에,..., p는 자동 회귀 방정식에 알려진 이전 값으로 대체(왜냐하면 우리가 그것의 기대 가치 와 동일하게, 그리고 unobs의 기대 가치 Xt으로 전망했다.erved 오류 항은 0입니다).자기 회귀 방정식의 출력은 관측되지 않은 첫 번째 기간의 예측값입니다.다음으로, 데이터를 아직 이용할 수 없는 다음 기간을 참조하기 위해 t를 사용한다. 다시 한 번 자기 회귀 방정식을 사용하여 예측을 한다. 즉, 현재 예측되는 기간보다 한 기간 전의 X 값을 알 수 없기 때문에 그 기대값(이전 예측 단계에서 발생하는 예측값)이 대신 사용된다.그런 다음 미래 기간에 대해 p 예측 후 모든 p 오른쪽 값이 이전 단계의 예측 값이 될 때까지 매번 예측 방정식의 오른쪽에 있는 하나 이상의 예측 값을 사용합니다.

이러한 방식으로 얻은 예측에 대한 불확실성의 네 가지 원천이 있다. (1) 자기 회귀 모델이 올바른 모델인지에 대한 불확실성, (2) 자기 회귀 방정식의 오른쪽에서 지연된 값으로 사용되는 예측 값의 정확성에 대한 불확실성, (3) au의 참 값에 대한 불확실성(4) 예측되는 기간의 오차항 ${\displaystyle {\theta }_{}}$ t${\displaystyle {}_{}}$\$displaystyle \varepsilon$ _${t},}$ 값에$$ 대한 불확실성.마지막 세 가지를 각각 정량화하고 조합하여 n단계 예측에 대한 신뢰 구간을 제공할 수 있습니다. 오른쪽 변수에 대한 추정값의 수가 증가하므로 신뢰 구간은 n이 증가할수록 넓어집니다.

예측 품질 평가

자기 회귀 모형의 예측 성능은 교차 검증을 사용하는 경우 추정이 완료되는 즉시 평가할 수 있습니다.이 접근법에서 초기에 사용 가능한 데이터의 일부는 매개변수 추정 목적으로 사용되었고, 일부(데이터 세트의 후반부에서 사용 가능한 관측치)는 표본 외 테스트를 위해 보류되었다.또는 파라미터 추정을 실시한 후 시간이 경과하면 더 많은 데이터를 이용할 수 있게 되고 새로운 데이터를 사용하여 예측 성능을 평가할 수 있게 된다.

어느 경우든 예측 성능에는 한 단계 앞선 성능과 n 단계 앞선 성능이라는 두 가지 측면이 있습니다.한 단계 전의 성능의 경우 추정된 모수는 예측되기 전의 모든 기간에 대해 X의 관측치와 함께 자기 회귀 방정식에 사용되며 방정식의 출력은 한 단계 전의 예측값입니다. 이 절차는 표본 밖의 각 관측치에 대한 예측을 구하는 데 사용됩니다.n단계 예측의 품질을 평가하기 위해 이전 섹션의 예측 절차를 사용하여 예측을 얻습니다.

다양한 기간 동안 X에 대한 일련의 예측값과 그에 상응하는 실제 값 세트가 주어진다면, 일반적인 평가 기법은 평균 제곱 예측 오차를 사용하는 것입니다. 다른 측정도 사용할 수 있습니다(예측#예측 정확도 참조).

측정된 예측 정확도를 해석하는 방법에 대한 질문이 발생한다. 예를 들어, 평균 제곱 예측 오류에 대한 "높음"(나쁜) 또는 "낮음"(좋은) 값은 무엇인가?비교할 수 있는 두 가지 포인트가 있습니다.첫째, 다른 모델링 가정 또는 다른 추정 기법에 따라 추정된 대체 모델의 예측 정확도를 비교 목적으로 사용할 수 있다.둘째, 표본 외 정확도 측정은 충분한 사전 데이터 값을 사용할 수 있는 표본 내 데이터 포인트(파라미터 추정에 사용됨)에 대해 계산된 동일한 측정값과 비교할 수 있습니다(즉, p 이전 데이터 포인트를 사용할 수 없는 첫 번째 데이터 포인트 삭제).모형이 가능한 한 표본 내 점을 적합하도록 특별히 추정되었기 때문에 일반적으로 표본 외 예측 성능이 표본 내 예측 성능보다 더 나쁠 수 있습니다.그러나 예측 품질이 표본 밖으로 "매우 많이" 악화되는 경우(정확하게 정의할 수 없음), 예보관은 성능에 만족할 수 있습니다.

「 」를 참조해 주세요.

• 이동평균모델
• 선형 차분 방정식
• 예측 분석
• 선형 예측 부호화
• 공명
• 레빈슨 재귀
• 오른스타인움렌벡법

메모들

레퍼런스

• Mills, Terence C. (1990). Time Series Techniques for Economists. Cambridge University Press.
• Percival, Donald B.; Walden, Andrew T. (1993). Spectral Analysis for Physical Applications. Cambridge University Press.
• Pandit, Sudhakar M.; Wu, Shien-Ming (1983). Time Series and System Analysis with Applications. John Wiley & Sons.

외부 링크

• Paul Bourke의 자동 회귀 분석(AR)
• 계량경제학 강의(토픽: Mark Thoma의 YouTube에서의 자기 회귀 모델)