헥사니

Hexany
정팔면체

음악 튜닝 시스템에서 얼버 윌슨에 의해 발명된 헥사니는 그의 콤비네이션 제품 세트에서 발견되는 가장 단순한 구조들 중 하나를 나타낸다.[1]

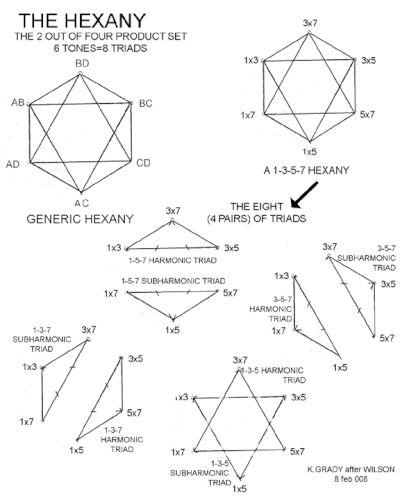
강장제를 내포하지 않는다는 뜻으로, 비중심적 구조라고 한다. 그것은 보통 무차별성에 의해 사용되는 불협화음 방법과는 반대로 자음 관계를 사용함으로써 이를 달성한다. 오일러-와 종종 그리고 혼란스럽게 겹쳐진다.Fokker속, Wilson's Combination 제품 세트(CPS)의 후속 스텔레이션은 이 속 바깥쪽에 있다. 오일러 포커 속은 출발점을 제외하고 1을 세트의 가능한 구성원으로 보지 못한다. 그의 콤비네이션 세트의 정점 수는 파스칼 삼각형의 숫자들을 따른다. 이 구조에서 육각형은 4요소 집합의 세 번째 단면이며 첫 번째 중심적이지 않은 단면이다. 헥사니는 Earv Wilson이 2*4 CPS로 약칭한 2-of-4 콤비네이션 제품 세트의 6개 노트에 붙인 이름이다.[2]

간단히 말해서 헥사니는 4세트 중 2세트다. 네 가지 요인과 두 가지 요인을 한 번에 하나씩 취하여 쌍으로 곱하는 방식으로 구성된다. 예를 들어 고조파 요인 1, 3, 5, 7은 1*3, 1*5, 1*7, 3*5, 3*7, 3*7, 5*7의 쌍으로 결합되어 1, 3, 5, 7 헥사니가 발생한다. 음은 대개 옥타브 이동하여 모두 같은 옥타브 안에 넣는데, 이는 간격 관계와 삼행의 조화에는 영향을 미치지 않는다. 옥타브가 해결책이 될 가능성은 윌슨의 개념 밖이 아니며 일반 키보드 위에 더 큰 조합 제품 세트를 놓는 경우에 사용된다.

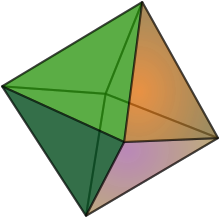
육면체는 팔면체와 유사하다고 생각할 수 있다. 음을 배열하여 각 점은 음을 나타내고, 각 가장자리는 간격을 나타내며, 각 점은 삼합창을 향하도록 한다. 따라서 8개의 그냥 억양삼중주를 가지고 있다. 각 삼중창은 다른 세개의 화음과 공통적으로 두개의 음을 가지고 있다. 각각의 3중창은 상반된 3음으로 대표되는 그것의 역행으로 단 한 번 발생한다. 팔면체의 가장자리는 정점 사이의 음악적 간격을 보여주는데, 보통 고조파 시리즈에서 자음 간격으로 선택된다. 포인트는 음악 음을 나타내고, 각 삼각형의 얼굴을 만드는 세 개의 음은 음악적 트라이애드를 나타낸다. 윌슨 역시 멜로 헥사니스의 사상을 지적하고 탐구했다.

튜닝

이것은 육각형의 3차원 버전을 보여준다.

직교 투영.

Hexanyfacets.gif

육각형은 표시된 삼각형과 그 사이의 연결선을 모두 포함하는 그림이다.



이 2D 구조에서 간격 관계는 동일하다. Kraig Grady 논문의 그림 2도 참조하십시오.[3]


예를 들어 정점이 3×5, 1×5, 5×7인 얼굴은 낮은 숫자의 고조파를 사용하여 5×(1, 3, 7)로 쓸 수 있으므로 오토날(주요형) 화음이다. 5×7, 3×7, 3×5는 숫자가 적은 하위조화법을 사용하여 3×5×7×(1/3, 1/5, 1/7)로 쓸 수 있기 때문에 유턴(소형) 화음이다.

이것을 1/1을 첫 번째 음으로 하는 전통적인 조화 구조로 만들기 위해, 모든 음을 먼저 옥타브까지 줄인다. 어브르(Erv)가 그것을 척도로 여기지 않고 아직 1/1을 가지고 있지 않기 때문에, 선택된 음은 모든 음을 옥타브까지 나누는 데 사용할 수 있다. 여기서 비율 표기법은 음의 빈도 비율을 보여준다. 1/1이 500헤르츠라면, 6/5는 600헤르츠 등.

파스칼 삼각형과의 관계

이 구조에서 하이퍼큐브에 대한 파스칼 삼각형의 전체 열은 1(단정점), 4(정점), 4(정점 테트라드), 6(헥사니), 4(또 다른 테트라드), 1을 운행한다. 이 아이디어는 다른 차원을 일반화하는데, 예를 들어, 5차원 입방체의 교차점은 데카니의 두 가지 버전을 제공하는데, 데카니는 테트라드, 트라이애드, 다이애드가 풍부한 10노트 척도로, 이 두 가지 버전에도 많은 헥사니를 포함하고 있다.[4] 6차원에서는 같은 구조가 20노트 에이코사니에게 주는데, 화음은 더욱 풍부하다. 펜타드, 테트라드, 트라이애드뿐만 아니라 육각류와 데카니도 있다.[4]

3차원 입방체의 경우, 일반적으로 전체 입방체를 하나의 8노트 눈금, 즉 8진수 눈금, 즉 교차점, 즉 1, 3진수, 3진수, 1진수, 1진수, 즉 입방체의 4대각선 중 하나를 따라 취한다.

Pascal의 조합 제품 세트 삼각형 좌표

첫 번째 행(제곱):
00
10 01
11

두 번째 행:
000
100 010 001 트라이어드(트리어드)
110 101 011 삼합집(三合集)
111

3열
0000
1000 0100 0010 0001 테트라드(삼각형 또는 3각형)
1100 1010 1001 01101 0101 0011 헥사니(옥타헤드론)
1110 1101 1011 0111 테트라드
1111

그곳의 팔면체는 사면체의 가장자리 이중 또는 수정 사면체의 가장자리 이중이다.

4열
00000
10000 01000 00100 00010 00001 펜타드(4-1600x 또는 펜타초론 – 4차원 사면체)
11000 10100 10010 10001 01100 010 01001 001101 00011 2)5 데카니(10정점, 수정 4-11x)
00111 01011 01101 01110 100111010101010101010101010111003)5 데카니(10정점)
01111 10111 11011 11101 1110 펜타드
11111

데카니의 기하학적 모양에 대한 수학적 이름인 수정 4단순은 디스펜타코론으로도 알려져 있다.

다섯째줄
000000
100000 010000 001000 000100 000010 000001 헥사드(5인치 또는 16진수 – 5차원 사면체)
110000 101000 100100 100010 100001 011000 010100 010010 010001 001000 001001 00010101 000101 000101 000011 2)6 펜타데카니(15정점, 수정 5-11x)
111000 110100 110010 110001 101100 1010101010101001 100101101 100011 011100 011101101 010101 010101 00110010 001011 000111 eikosany(20정점 2방향 5-11x)
0011 010111 01101 01110011 01110 01110101010101010101010101011101101101110111001)6 펜타데카니(15정점)
011111 10111 1101111 11101 11101 111110 16진수
111111


데카니는 4단계의 엣지 듀얼이다. 마찬가지로 펜타데카니의 기하학적 수치는 5단계의 가장자리 이중이다. 데카니 캠은 4-심플렉스 가장자리의 중간점을 결합하여 만들어지며, 펜타데카니와 5-심플렉스도 이와 유사하다.


마찬가지로 1/2만큼 스케일링할 때 데카니 정점은 4단계의 중간점으로 이동하고, 펜타데카니 정점은 5단계의 중간점으로 이동하며, 따라서 모든 상위 차원으로 이동한다.

1/3만큼 크기를 조정할 때 에이코사니 정점은 5-심플렉스 2D 면의 중심으로 이동한다. 3D 큐브 111에서 1/3로 스케일링할 때 각 에지 벡터는 100 010 001의 중간점으로 이동하며, 여기서 각 에지 벡터는 큐브의 긴 대각선을 따라 동일한 거리를 미분한다. 11100은 코드 10000 01000 00100으로 등방 삼각형의 중앙으로 이동하며 다른 모든 아이코사니 정점에서도 유사하다.

아이코사니의 기하학적 도형은 3D와 4D 면도 가지고 있기 때문에 2D 면의 이중인 5-simplex 또는 양방향인 5-simplex의 페이스 듀얼이다.

모든 상위 치수의 3)7, 3)8 등의 수치와 유사한 그림이다.

마찬가지로 8차원에서도 8개 중 4개의 순열체를 사용하여 얻은 수치는 1111이 3D 정규 4면 1000 0100 0010 0001 등 3D 일반 4면 중앙으로 이동하기 때문에 7-심플렉스 또는 3-정립 7-심플렉스 이중이다.

음악으로

크라이그 그래디, 다니엘 제임스 울프, 조셉 페어슨 등 작곡가들은 육각형을 바탕으로 한 피치 구조를 사용해 왔다.[citation needed]

참고 항목

참조

  1. ^ 샬머스, 존 H. (1993) 테트라코드의 사단: 음악적 음계구축의 프롤레고멘, 페이지 116. 개구리 피크 뮤직. ISBN978-0-945996-04-0.
  2. ^ [author missing] (1993). 음악 작품, 이슈 55-60, 페이지 43. 음악 갤러리.
  3. ^ Grady, Kraig (1991). "Ervin Wilson's Hexany" (PDF). Just Intonation. 7 (1): 8–11.
  4. ^ a b Wilson, Erv. "D'Alessandro, Like a Hurricane, Figures 6b, 6c, 19, 20 and 20b" (PDF). Xenharmonikon. 12: 10, 21.

추가 읽기

외부 링크