복합폴리토프

기하학에서 복합 폴리토프는 폴리토프를 실제 공간에 있는 폴리토프를 복잡한 힐버트 공간의 유사 구조로 일반화한 것으로, 각각의 실제 차원은 상상의 차원과 동반된다.

복합 폴리토프는 복잡한 점, 선, 평면 등의 집합체로 이해될 수 있는데, 여기서 모든 점은 여러 선의 교차점, 여러 평면의 모든 선 등의 결합점이다.

정확한 정의는 구성인 일반 복합 폴리토페스에 대해서만 존재한다. 일반 복합 폴리토페스는 완전히 특징지어졌으며, 콕시터가 개발한 상징적 표기법을 사용하여 설명할 수 있다.

완전히 규칙적이지 않은 일부 복잡한 폴리토페어도 설명되어 있다.

정의 및 소개

복합선 $\mathbb {C} ^{1}$ $\mathbb {C} ^{1}$ ${\$ }은 $($ 는) 실제 좌표를 가진 차원과 가상 좌표를 가진 차원을 가지고 $\mathbb {C} ^{1}$ 있다. 양쪽 차원에 실제 좌표를 적용하면 실수에 걸쳐 2차원이 주어진다고 한다. 상상의 축이 이와 같이 표시된 실제 평면을 아르간드 도표라고 한다. 이 때문에 복잡한 평면이라고 부르기도 한다. 복잡한 2-공간(복잡한 평면이라고도 함)은 그러므로 실재 위에 4차원 공간이며, 더 높은 차원에서도 그러하다.

복잡한 n-공간에서 복잡한 n-폴리토프는 실제 n-공간에서 실제 n-폴리토프의 아날로그다.

실제 라인의 포인트 순서(또는 관련 조합 속성)에 대한 자연적인 복잡한 아날로그는 없다. 이 때문에 복잡한 폴리토프는 연속된 표면으로 볼 수 없으며 실제 폴리토프가 하는 방식으로 내부를 구속하지 않는다.

일반 폴리토페스의 경우 대칭의 개념을 이용하여 정확한 정의를 내릴 수 있다. 어떤 규칙적인 폴리토프의 경우 대칭군(여기서 복잡한 반사군, 셰퍼드군)은 깃발, 즉 평면에 포함된 선에 포함된 점의 내포된 순서에 대해 전적으로 작용한다.

보다 완전하게, 치수 n의 복합 유니터리 공간 V의 아핀 서브 스페이스(혹은 플랫)의 집합 P는 다음과 같은 조건을 만족하는 경우 일반 복합 폴리토프라고 한다.^[1]^[2]

매 $-1$ ≤ $i$ < $j$ < $k$ ≤ $n$ 에 $대하여$ , F가 치수 i의 P에 플랫이고 $H$ 가 $치수$ k의 플랫인 경우, 치수 j의 P에 $F$ $\subset$ $G$ ⊂ $H$ 와 같은 평형 G가 적어도 2개 있다.
모든 $i$ 에 대해, $-1$ ≤ i < $j$ - 2, $j$ ≤ n, $F g$ G가 치수 i, j의 P 평판인 경우, F와 G 사이의 평판 세트가 연결되고, 이 집합의 어떤 멤버로부터도 일련의 함정에 의해 다른 어떤 멤버로 가져올 수 있다.
P를 고정하는 V의 단일 변환의 하위 집합은 P 평면의 F $flags 0$ F ⊂ $F 1 \dots$ … $\subset F n$ 플래그(모든 i에 대한 차원 i의 $F i$ with)에 전이된다.

(여기서는 빈 세트를 의미하는 차원 -1의 평면을 취한다.) 그러므로, 정의에 따르면, 규칙적인 복합 폴리토페스는 복잡한 단일 공간에서의 구성이다.

규칙적인 복합 폴리토페스는 셰퍼드(1952년)에 의해 발견되었고, 이 이론은 콕시터(1974년)에 의해 더욱 발전되었다.

일반 복합 폴리곤 {4}₂의 세 가지 보기

이 복잡한 폴리곤은 a..h로 라벨이 붙은 8개의 가장자리(복잡한 선)와 16개의 꼭지점을 가지고 있다. 각 가장자리에는 정점 4개가 있고 각 꼭지점에는 두 개의 가장자리가 교차한다. 왼쪽 이미지에서 윤곽선 정사각형은 폴리토프의 요소가 아니라 단지 같은 복잡한 선에 놓여 있는 정점을 식별하는 데 도움을 주기 위해 포함되어 있다. 왼쪽 이미지의 팔각형 둘레는 폴리토프의 요소가 아니라 페트리 폴리곤이다.^[3] 중간 이미지에서 각 가장자리는 실제 선으로 표현되며 각 선에 있는 네 개의 꼭지점이 더 선명하게 보인다.	16개의 꼭지점을 크고 검은 점으로, 8개의 4-edge를 각 가장자리 내 경계 정사각형으로 나타내는 원근 스케치. 녹색 길은 왼손 이미지의 팔각형 둘레를 나타낸다.

등가 치수의 복잡한 공간에 복합 폴리토프가 존재한다. 예를 들어 복합 폴리곤의 정점은 복합 평면 $\mathbb {C} ^{2}$ 2 ${\$ ^{ $2}},$ 가장자리는 복합 선 $\mathbb {C} ^{1}$ $\mathbb {C} ^{1}$ ${\$ 1}이며 평면의 (아핀) 하위 영역으로 존재하며 $\mathbb {C} ^{1}$ 정점에서 교차한다. 따라서 가장자리에는 하나의 복잡한 숫자로 구성된 좌표계가 주어질 수 있다.^{[clarification needed]}

일반 복합 폴리토프에서 가장자리에 있는 정점들은 그 중심에 대칭적으로 배열되는데, 이것은 종종 가장자리 좌표계의 원점으로 사용된다(실제 경우에는 중심은 가장자리의 중간점에 불과하다). 대칭은 중심점에 대한 복잡한 반사에서 발생한다. 이 반사는 정점의 크기를 변경하지 않고 그대로 두지만, 그 주장을 고정된 양만큼 변경하여 순서대로 다음 정점의 좌표로 이동시킨다. 따라서 가장자리의 정점이 $x^{p}-1=0$ p $x^{p}-1=0$ - $x^{p}-1=0$ = $x^{p}-1=0$ $x^{p}-1=0$ 등식을 만족한다고 가정할 수 있으며 여기서 $x^{p}-1=0$ p는 입사 정점의 수입니다. 따라서 가장자리의 아르간드 도표에서 꼭지점은 원점을 중심으로 한 정규 다각형의 정점에 놓여 있다.

정규 복합 폴리곤 4{4}2의 실제 투영 3개가 위에 설명되어 있으며 가장자리 a, b, c, d, e, f, g, h가 있다. 그것은 16개의 정점들을 가지고 있는데, 이것은 명확성을 위해 개별적으로 표시되지 않았다. 각 가장자리는 4개의 꼭지점이 있고 각 꼭지점은 2개의 가장자리에 있으므로 각 가장자리는 4개의 다른 가장자리와 만난다. 첫 번째 다이어그램에서 각 가장자리는 정사각형으로 표시된다. 정사각형의 옆면은 다각형의 부분이 아니라 순수하게 네 개의 꼭지점을 시각적으로 연결하기 위해 그려진다. 가장자리는 대칭적으로 배열되어 있다. (참고: 도표는 테서락트의 B₄ Coxeter 평면 투영과 유사하게 보이지만 구조적으로는 다르다.)

중간도는 명료성을 위해 팔각대칭을 포기한다. 각 가장자리는 실제 선으로 표시되며, 두 선의 각 만남 지점은 정점이다. 다양한 가장자리 사이의 연결성이 뚜렷이 보인다.

마지막 도표는 3차원으로 투영된 구조의 맛을 보여준다: 두 정점의 정점들은 사실 같은 크기지만 네 번째 차원에서는 다른 거리에서 원근법으로 보인다.

일반 콤플렉스 1차원 폴리탑

p = 2, 3, 4, 5, 6의 정규 폴리곤으로 아르간드 평면에 표현되는 복잡한 1 폴리토프는 검은색 정점을 가지고 있다. p 꼭지점의 중심은 빨간색으로 보인다. 다각형의 측면은 대칭 발생기의 한 가지 응용을 나타내며, 각 꼭지점을 다음 반시계방향 복사본에 매핑한다. 복합 1폴리토프는 가장자리가 없을 수 있고(복잡한 가장자리인 경우가 많으며) 꼭지 요소만 포함하기 때문에 이러한 다각측면은 폴리토프의 가장자리 요소가 아니다.

실제 1차원 폴리토프는 $\mathbb {R} ^{1}$ 라인 R $\mathbb {R} ^{1}$ {\ $displaystyle \mathb{R} ^{1}$ 에 닫힌 세그먼트로 존재하며 $\mathbb {R} ^{1}$ 라인의 두 끝점 또는 정점에 의해 정의된다. 그것의 슐레플리 기호는 {}이다.

유사하게, 복합 1 폴리토프는 복합 선 C $\mathbb {C} ^{1}$ ${\$ 에 p 꼭지점 집합으로 존재한다 $\mathbb {C} ^{1}$ 이러한 점은 Argand 도표(x,y)=x+iy에서 점 집합으로 나타낼 수 있다. 정규 콤플렉스 1차원 폴리토프 {}에는 아간드 평면에서 볼록한 정규 폴리곤 {p}을(를) 형성하도록 p (p ≥ 2) 꼭지점이 배열되어 있다.^[4]

실제 라인의 포인트와 달리 복합 라인의 포인트는 자연스러운 순서가 없다. 따라서 실제 폴리토페와는 달리 내부는 정의할 수 없다.^[5] 그럼에도 불구하고 아르간드 평면의 경계형 일반 다각형으로 여기와 같이 복잡한 1폴리토프를 그리는 경우가 많다.

실제 가장자리는 거울을 가로지르는 점과 반사 이미지 사이의 선으로 생성된다. 단일 반사 순서 2는 중심 주위를 180도 회전하는 것으로 볼 수 있다. 발전기 지점이 반사선에 있거나 중심에 있으면 가장자리가 비활성화된다.

일반적인 실제 1차원 폴리토프는 빈 Schléfli 기호 {} 또는 Coxeter-Dynkin 도표로 표현된다. Coxeter-Dynkin 다이어그램의 점이나 노드는 그 자체로 반사 발생기를 나타내는 반면, 노드 주위의 원은 발생기 점이 반사 위에 있지 않음을 의미하므로 반사 이미지는 그 자체와 구별되는 점이다. $\mathbb {C} ^{1}$ 로 $\mathbb {C} ^{1}$ 1 ${\$ ^1}의 $\mathbb {C} ^{1}$ 일반 복합 폴리토프에는 정점을 포함하는 모든 양의 정수 p, 2 이상의 Coxeter-Dynkin 다이어그램이 있다 $\mathbb {C} ^{1}$ . p는 2일 경우 억제될 수 있다. 또한 빈 Schléfli 기호 {}, _p}{, {}_p 또는 {2}(₁으)로 나타낼 수 있다. 1은 존재하지 않는 반사를 나타내는 공칭 자리 표시자 또는 기간 1 ID 생성자다. (0 폴리토프, 진짜 또는 복잡한 것이 포인트로, } { 또는 {2}(으)로 표현된다.)₁

대칭은 Coxeter 다이어그램으로 표시되며, 대신 Coxeter 표기법으로 [], [] _p또는 ],_p [2]₁ 또는 [1]_p로 설명할 수 있다. 대칭은 주기적 그룹, 순서 p와 이형이다.^[6] []의 하위 그룹은 전체 d, [], 여기서 d≥2이다.

에 대한 유니터리 연산자 발생기는 시계 반대 방향으로 2㎛/p 라디안 회전으로 보이며, 단일 유니터리 반사의 순차적 적용에 의해 에지가 생성된다. p 정점이 있는 1 폴리토프의 단일 반사 발생기는 $e 2π i / p$ = $cos(2㎛/ p)$ + i $sin$ (2 $㎛/ p)$ 이다. p = 2일 때 발전기는 e^πi = –1로 실제 평면의 점 반사와 동일하다.

더 높은 복합 폴리탑에서 1 폴리탑은 p-edge를 형성한다. 2-엣지는 두 개의 꼭지점을 포함하고 있다는 점에서 일반적인 실제 가장자리와 유사하지만 실제 선에 존재할 필요는 없다.

일반 복합 폴리곤

1폴리토프는 p를 무제한으로 가질 수 있지만, 이중 프리즘 폴리곤 {4}₂을(를) 제외한 유한 일반 복합 폴리곤은 5 에지(펜타곤 가장자리) 원소로 제한되며, 무한 일반 아페이로곤 역시 6 에지(헥사형 가장자리) 원소를 포함한다.

공증

셰퍼드 변형 슐레플리 표기법

셰퍼드(Shephard)는 원래 슐래플리의 일반 폴리토페스에 대한 표기법을 변형한 형태를 고안했다. p-edge로₁ 경계된 폴리곤에 대해, p-set를₂ 정점 그림으로 하고, p-set를 순서 g의 전체 대칭 그룹으로 하고, 폴리곤을₁ p(g)p로₂ 나타낸다.

이때 정점 V의 수는 g/p이고₂ 가장자리 E의 수는₁ g/p이다.

위에서 설명한 복합 폴리곤은 8개의 사각 모서리(p₁=4)와 16개의 꼭지점(p₂=2)이 있다. 여기서 우리는 수정된 Schléfli 기호 4(32)2를 제공하는 g = 32를 알아낼 수 있다.

콕세터의 개정 슐레플리 표기법

보다 현대적인 표기법 {q}_p₂은 콕시터(Coxeter)에 기인하며,^[7] 집단 이론에 근거한다. 대칭군으로서, 그것의 상징은 [q]_p₂이다.

대칭군[q]_p₂은 2개의 발전기 R₁, R으로₂ 표시되며 여기서₁^p₁: R = R₂^p₂ = I. q가 짝수이면 (RR₂₁)^q/2 = (RR₁₂). ^q/2q가 홀수이면 (RR₂₁)^(q-1)/2R₂ = (RR₁₂)^(q-1)/2R₁. q가 홀수일 때는₁ p=p₂.

[4]₂의 경우 R₁⁴ = R₂² = I, (RR₂₁)² = (RR₁₂)²가 있다.

[5]₃의 경우 R₁³ = R₂³ = I, (RR₂₁)²R₂ = (RR₁₂)²R이₁ 있다.

콕시터-딘킨 도표

Coxeter는 또한 복잡한 폴리토페스에 Coxeter-Dynkin 다이어그램의 사용을 일반화했다. 예를 들어 복합 폴리곤 {q}_r이(가) 표현되고 등가 대칭 그룹인 [q]_r은 링이 없는 다이어그램이다. 노드 p와 r은 평면에서 p와 r 이미지를 생성하는 미러를 나타낸다. 다이어그램에 라벨이 부착되지 않은 노드에는 2개의 라벨이 내재되어 있다. 예를 들어 실제 일반 폴리곤은 {q},₂ {q} 또는 .

한 가지 제한 사항, 홀수 분기 주문에 의해 연결된 노드는 동일한 노드 주문을 가져야 한다. 그렇지 않으면, 이 그룹은 요소들이 겹치는 "별" 다각형을 만들 것이다. 그래서 평범하고, 반면에 별빛은 좋다.

12개 어레듀커블 셰퍼드 그룹

부분군 지수 관계를 가진 12개의 수정 불가능한 Shephard 그룹.^[8] 부분군 지수 2는 실제 반사를 제거함으로써 관련된다.
_p[2q]₂ --> [q],_p 색인 2.
_p[4]_q --> [q],_p 색인 q.

_p[4]₂ 부분군: p=2,3,4...
_p[4]₂ --> [p], 색인 p
_p[4]₂ --> []×[],_p 색인 2

Coxeter는 이 $\mathbb {C} ^{2}$ 복합 $\mathbb {C} ^{2}$ 폴리곤 $목록$ 을 C 2 ${\displaystyle \$ mathb {C} $^{2$ 일반 복합 폴리곤, {q}_r 또는 에는 p-edge와 r-곤 정점 수치가 있다. _p{q}_r은(p+r)q>pr(q-2)일 경우 유한 폴리토프다.

그것의 대칭은 콕시터 그룹과 유사하게 셰퍼드 그룹이라고 불리는 [q]_r로 쓰이면서 동시에 단일 반사도 허용된다.

비별 그룹의 경우, $g=8/q\cdot (1/p+2/q+1/r-1)^{-2}$ [q]_r의 순서는 g $g=8/q\cdot (1/p+2/q+1/r-1)^{-2}$ = 8 $g=8/q\cdot (1/p+2/q+1/r-1)^{-2}$ / $g=8/q\cdot (1/p+2/q+1/r-1)^{-2}$ $g=8/q\cdot (1/p+2/q+1/r-1)^{-2}$ ( $g=8/q\cdot (1/p+2/q+1/r-1)^{-2}$ / $g=8/q\cdot (1/p+2/q+1/r-1)^{-2}$ + 2 $g=8/q\cdot (1/p+2/q+1/r-1)^{-2}$ / $g=8/q\cdot (1/p+2/q+1/r-1)^{-2}$ + 1 / $g=8/q\cdot (1/p+2/q+1/r-1)^{-2}$ / $g=8/q\cdot (1/p+2/q+1/r-1)^{-2}$ - $g=8/q\cdot (1/p+2/q+1/r-1)^{-2}$ ) $g=8/q\cdot (1/p+2/q+1/r-1)^{-2}$ - $g=8/q\cdot (1/p+2/q+1/r-1)^{-2}$ ${\$ 스타일 $g=8/q\cdot (1/p+2/q+1/r-1)^{-22$ ^[9]

The Coxeter number for _p[q]_r is $h=2/(1/p+2/q+1/r-1)$ , so the group order can also be computed as $g=2h^{2}/q$ . A regular complex polygon can be drawn in orthogonal projection with h-gonal symmetry.

복잡한 다각형을 생성하는 2위 솔루션은 다음과 같다.

그룹	G₃=G(q,1,1)	G₂=G(p,1,2)	G₄	G₆	G₅	G₈	G₁₄	G₉	G₁₀	G₂₀	G₁₆	G₂₁	G₁₇	G₁₈
	₂[q]₂, q=3,4...	_p[4]₂, p=2,3...	₃[3]₃	₃[6]₂	₃[4]₃	₄[3]₄	₃[8]₂	₄[6]₂	₄[4]₃	₃[5]₃	₅[3]₅	₃[10]₂	₅[6]₂	₅[4]₃

주문	2q	2p²	24	48	72	96	144	192	288	360	600	720	1200	1800
h	q	2p	6	12			24			30		60

홀수 q,₂ [3], [3],₃ [3],₃ [3], [3], [3],₃₂ [3],₂₂ [5],₂ [5], ₂[₂5], [7], [9],₂ [11]₂이 있다.

p와 r이 동일하지 않은 다른 전체 q는 , , , , , , 및 .와 같은 기본 도메인이 중첩된 별을 가진 그룹을 생성한다.

{q}_r의 이중 폴리곤은 {q}_p이다. {q}_p 형식의 다각형은 자체 이중이다. [2q]₂ 형식의 그룹은 대칭[q]_p이 절반이므로 일반 다각형은 quasiregular와 동일하다. 또한, 노드 순서가 같은 일반 다각형은 교대형 구조를 가지며, 인접 모서리가 두 가지 다른 색상이 되도록 한다.^[10]

그룹 순서 g는 정점과 에지의 총 수를 계산하는 데 사용된다. 그것은 꼭지점과 가장자리가 g/p 될 것이다. p=r일 때는 정점과 가장자리 수가 같다. 이 조건은 q가 홀수일 때 필요하다.

행렬 생성기

그룹 p[q]r, 는 두 개의 행렬로 나타낼 수 있다.^[11]


이름	R₁	R₂
주문	p	r
매트릭스	$\left[{\pi{smallmatrix}e^{2\pi i/p}&0\\(e^{2\pi i/p}-1)k&1\\\end{smallmatrix}\right]}$	$\left[{\pi{smallmatrix}1&(e^{2\pi i/r}-1)k\0&e^{2\pi i/r}\\end{smallmatrix}\right]}$

와 함께

k=

{\sqrt {\frac {cos({\frac {\pi }{p}}-{\frac {\pi }{r}})+cos({\frac {2\pi }{q}})}{2\sin {\frac {\pi }{p}}\sin {\frac {\pi }{r}}}}}

예


이름	R₁	R₂
주문	p	q
매트릭스	$\left[{\pi{smallmatrix}e^{2\pi i/p}\0&1\\\end{smallmatrix}}\오른쪽]$	$\left[{\put{smallmatrix}1&0\0&e^{2\pi i/q}\\end{smallmatrix}\오른쪽]}$


이름	R₁	R₂
주문	p	2
매트릭스	$\left[{\pi{smallmatrix}e^{2\pi i/p}\0&1\\\end{smallmatrix}}\오른쪽]$	$\left[{\\\smallmatrix}0&1\1&0\\\end{smallmatrix}\오른쪽]$


이름	R₁	R₂
주문	3	3
매트릭스	$\left[{\preason{smallmatrix}{\frac{-1+{\sqrt{3}}{3}}{3+{3}}}{2}}&1\nd{smallmatrix}\right]}}$	$\left[{\\smallmatrix}1&}{-3+{\sqrt{3}}{{}}}{{{1+{\sqrt{3}i}}{2}}\\nd{smallmatrix}\right]}}$


이름	R₁	R₂
주문	4	4
매트릭스	$\left[{\\\smallmatrix}i&0\0\1\\\end{smallmatrix}\오른쪽]$	$\left[{\\\smallmatrix}1&0\0&i\\\end{smallmatrix}\오른쪽]$


이름	R₁	R₂
주문	4	2
매트릭스	$\left[{\\\smallmatrix}i&0\0\1\\\end{smallmatrix}\오른쪽]$	$\left[{\\\smallmatrix}0&1\1&0\\\end{smallmatrix}\오른쪽]$


이름	R₁	R₂
주문	3	2
매트릭스	$\left[{\preason{smallmatrix}{\frac{-1+{\sqrt{3}}{3}}{3+{3}}}{2}}&1\nd{smallmatrix}\right]}}$	$\left[{\\\smallmatrix}1&-2\0&-1\\\end{smallmatrix}\오른쪽]$

일반 복합 폴리곤의 열거

Coxeter는 일반 복합 폴리토페스의 표 III에 복합 폴리곤을 열거했다.^[12]

그룹	주문	콕시터 번호를 붙이다	폴리곤		정점	가장자리		메모들
G(q,q,2) ₂[q]₂ = [q] q=2,3,4,...	2q	q	₂{q}₂		q	q	{}	리얼 레귤러 폴리곤 와 같다 q 짝수인 것과 같다.

그룹	주문	콕시터 번호를 붙이다	폴리곤		정점	가장자리		메모들
G(p,1,2) _p[4]₂ p=2,3,4,...	2p²	2p	p(2p²)2	_p{4}₂	p²	2p	_p{}	{}×{}_p와 동일하거나 $\mathbb {R} ^{4}$ $\mathbb {R} ^{4}$ ${\$ p-pduoprism으로 표현 $\mathbb {R} ^{4}$
G(p,1,2) _p[4]₂ p=2,3,4,...	2p²	2p	2펜스²	₂{4}_p	2p	p²	{}	$\mathbb {R} ^{4}$ $\mathbb {R} ^{4}$ ${\$ p-p 듀오피라미드로 표현 $\mathbb {R} ^{4}$
G(2,1,2) ₂[4]₂ = [4]	8	4		₂{4}₂ = {4}	4	4	{}	{}×{}와 동일하거나 리얼 스퀘어
G(3,1,2) ₃[4]₂	18	6	6(18)2	₃{4}₂	9	6	₃{}	{}×{}₃와 동일하거나 $\mathbb {R} ^{4}$ $\mathbb {R} ^{4}$ ${\$ 3-3 duoprism으로 표현 $\mathbb {R} ^{4}$
G(3,1,2) ₃[4]₂	18	6	2(18)3	₂{4}₃	6	9	{}	$\mathbb {R} ^{4}$ $\mathbb {R} ^{4}$ ${\$ 3-3 듀오피라미드로 표현 $\mathbb {R} ^{4}$
G(4,1,2) ₄[4]₂	32	8	8(32)2	₄{4}₂	16	8	₄{}	{}×{}₄와 동일하거나 $\mathbb {R} ^{4}$ $\mathbb {R} ^{4}$ ${\$ 4-4 듀오프리즘 또는 {4,3,3}으로 표현 $\mathbb {R} ^{4}$
G(4,1,2) ₄[4]₂	32	8	2(32)4	₂{4}₄	8	16	{}	$\mathbb {R} ^{4}$ $\mathbb {R} ^{4}$ ${\$ 4-4 듀오피라미드 또는 {3,4}으로 표현 $\mathbb {R} ^{4}$
G(5,1,2) ₅[4]₂	50	25	5(50)2	₅{4}₂	25	10	₅{}	{}×{}₅와 동일하거나 $\mathbb {R} ^{4}$ $\mathbb {R} ^{4}$ ${\$ 5-5 듀오프리즘으로 표현 $\mathbb {R} ^{4}$
G(5,1,2) ₅[4]₂	50	25	2(50)5	₂{4}₅	10	25	{}	$\mathbb {R} ^{4}$ $\mathbb {R} ^{4}$ ${\$ 5-5 듀오피라미드로 표현 $\mathbb {R} ^{4}$
G(6,1,2) ₆[4]₂	72	36	6(72)2	₆{4}₂	36	12	₆{}	{}×{}₆와 동일하거나 $\mathbb {R} ^{4}$ $\mathbb {R} ^{4}$ ${\$ 6-6 duoprism으로 표현 $\mathbb {R} ^{4}$
G(6,1,2) ₆[4]₂	72	36	2(72)6	₂{4}₆	12	36	{}	$\mathbb {R} ^{4}$ $\mathbb {R} ^{4}$ ${\$ 6-6 듀오피라미드로 표현 $\mathbb {R} ^{4}$
G₄=G(1,1,2) ₃[3]₃ <2,3,3>	24	6	3(24)3	₃{3}₃	8	8	₃{}	뫼비우스-칸토르 구성 와 같은 자기 만족. $\mathbb {R} ^{4}$ $\mathbb {R} ^{4}$ ${\$ {3,3,4}으로 표현 $\mathbb {R} ^{4}$
G₆ ₃[6]₂	48	12	3(48)2	₃{6}₂	24	16	₃{}	와 같은
				₃{3}₂	24	16	₃{}	별이 총총한 다각형
			2(48)3	₂{6}₃	16	24	{}
				₂{3}₃	16	24	{}	별이 총총한 다각형
G₅ ₃[4]₃	72	12	3(72)3	₃{4}₃	24	24	₃{}	와 같은 자기 만족. $\mathbb {R} ^{4}$ $\mathbb {R} ^{4}$ ${\$ {3,4,3}으로 표현 $\mathbb {R} ^{4}$
G₈ ₄[3]₄	96	12	4(96)4	₄{3}₄	24	24	₄{}	와 같은 자기 만족. $\mathbb {R} ^{4}$ $\mathbb {R} ^{4}$ ${\$ {3,4,3}으로 표현 $\mathbb {R} ^{4}$
G₁₄ ₃[8]₂	144	24	3(144)2	₃{8}₂	72	48	₃{}	와 같은
				₃{8/3}₂	72	48	₃{}	와 같은 별 모양의 다각형
			2(144)3	₂{8}₃	48	72	{}
				₂{8/3}₃	48	72	{}	별이 총총한 다각형
G₉ ₄[6]₂	192	24	4(192)2	₄{6}₂	96	48	₄{}	와 같은
			2(192)4	₂{6}₄	48	96	{}
				₄{3}₂	96	48	{}	별이 총총한 다각형
				₂{3}₄	48	96	{}	별이 총총한 다각형
G₁₀ ₄[4]₃	288	24	4(288)3	₄{4}₃	96	72	₄{}
		12		₄{8/3}₃	96	72	₄{}	별이 총총한 다각형
		24	3(288)4	₃{4}₄	72	96	₃{}
		12		₃{8/3}₄	72	96	₃{}	별이 총총한 다각형
G₂₀ ₃[5]₃	360	30	3(360)3	₃{5}₃	120	120	₃{}	와 같은 자기 만족. $\mathbb {R} ^{4}$ $\mathbb {R} ^{4}$ ${\$ {3,3,5}으로 표현 $\mathbb {R} ^{4}$
G₂₀ ₃[5]₃	360	30		₃{5/2}₃	120	120	₃{}	자화자찬, 별이 총총한 다각형
G₁₆ ₅[3]₅	600	30	5(600)5	₅{3}₅	120	120	₅{}	와 같은 자기 만족. $\mathbb {R} ^{4}$ $\mathbb {R} ^{4}$ ${\$ {3,3,5}으로 표현 $\mathbb {R} ^{4}$
G₁₆ ₅[3]₅	600	10		₅{5/2}₅	120	120	₅{}	자화자찬, 별이 총총한 다각형
G₂₁ ₃[10]₂	720	60	3(720)2	₃{10}₂	360	240	₃{}	와 같은
				₃{5}₂				별이 총총한 다각형
				₃{10/3}₂				와 같은 별 모양의 다각형
				₃{5/2}₂				별이 총총한 다각형
			2(720)3	₂{10}₃	240	360	{}
				₂{5}₃				별이 총총한 다각형
				₂{10/3}₃				별이 총총한 다각형
				₂{5/2}₃				별이 총총한 다각형
G₁₇ ₅[6]₂	1200	60	5(1200)2	₅{6}₂	600	240	₅{}	와 같은
		20		₅{5}₂				별이 총총한 다각형
		20		₅{10/3}₂				별이 총총한 다각형
		60		₅{3}₂				별이 총총한 다각형
		60	2(1200)5	₂{6}₅	240	600	{}
		20		₂{5}₅				별이 총총한 다각형
		20		₂{10/3}₅				별이 총총한 다각형
		60		₂{3}₅				별이 총총한 다각형
G₁₈ ₅[4]₃	1800	60	5(1800)3	₅{4}₃	600	360	₅{}
		15		₅{10/3}₃				별이 총총한 다각형
		30		₅{3}₃				별이 총총한 다각형
		30		₅{5/2}₃				별이 총총한 다각형
		60	3(1800)5	₃{4}₅	360	600	₃{}
		15		₃{10/3}₅				별이 총총한 다각형
		30		₃{3}₅				별이 총총한 다각형
		30		₃{5/2}₅				별이 총총한 다각형

일반 복합 폴리곤의 시각화

{2r}_q 형식의 다각형은 p-edge의 q 컬러 세트로 시각화할 수 있다. 각각의 p-edge는 얼굴이 없는 반면, 일반 다각형으로 보인다.

복합 폴리곤 {r}_q의 2D 직교 투영

{4}_q 형태의 다각형을 일반화된 직교라고 한다. 그들은 정점을 4D q-q 듀오피라미드와 공유하며, 정점은 2-edge로 연결된다.

₂{4},₂ 정점 4개 및 가장자리 4개
₂{4},₃ 정점 6개 및 가장자리 9개 포함^[13]
₂{4},₄ 정점 8개 및 가장자리 16개 포함
₂{4},₅ 정점 10개 및 가장자리 25개 포함
₂{4},₆ 정점 12개 및 가장자리 36개
₂{4},₇ 14개의 꼭지점 및 49개의 가장자리
₂{4},₈ 16개의 꼭지점 및 64개의 가장자리
₂{4},₉ 정점 18개 및 가장자리 81개
₂{4},₁₀ 정점 20개 및 가장자리 100개 포함

복합 다각형 {4}₂

{4}₂ 형식의 다각형을 일반화된 하이퍼큐브(다각형용 사각형)라고 한다. 그들은 4D p-p 듀오프리스ms, p-edge로 연결된 정점과 정점을 공유한다. 정점은 녹색으로 그리고 p-edge는 빨강과 파랑으로 번갈아 그려진다. 홀수 치수가 겹치는 정점을 중심에서 이동하기 위해 원근법이 약간 왜곡된다.

₂{4},₂ 또는 , 꼭지점 4개 및 2-점 4개
₃{4},₂ 또는 , 9개의 꼭지점 및 6개(정점) 3-점수^[13]
₄{4},₂ 또는 , 16개의 꼭지점 및 8개(정사각형) 4-제곱
₅{4},₂ 또는 , 25개의 꼭지점 및 10개(정점) 5개점
₆{4},₂ 또는 , 36개의 꼭지점 및 12개의 (사각형) 6개점
₇{4},₂ 또는 , 49개의 꼭지점 및 14개의 (헵대형)7-118
₈{4},₂ 또는 , 64개의 꼭지점 및 16개의 (8개) 8개점
₉{4},₂ 또는 , 정점 81개 및 (각각) 18개 9개
정점이 100인 {4₁₀},₂ 또는 , 20개(각각형) 10개인 경우

복잡한 다각형 {4}₂의 3D 투시 투영. 듀얼 {4}_p: 가장자리 내부에 정점을 추가하고, 정점 대신 가장자리를 추가함으로써 보인다.

₃{4},₂ 또는 9개의 꼭지점, 2개 세트의 3-세로 6개
정점 6개, 에지 9개 3세트인₂ {4}₃
₄{4},₂ 또는 16개의 꼭지점, 2개의 색 세트로 된 8개의 4-모서리, 채워진 사각형 4-모양
₅{4},₂ 또는 25개의 꼭지점, 10개의 5개의 5개의 색상 세트

기타 복합 폴리곤 {r}₂

₃{6},₂ 또는 , 검은색 24개의 꼭지점, 빨간색과 파란색^[14] 3개 세트의 2개 세트에 16개의 3개 색상이 있음
₃{8},₂ 또는 , 검정색에 72개의 꼭지점, 빨간색과 파란색에^[15] 3개 세트의 3개 세트에 48개의 3개 색상이 있음

복잡한 다각형의 2D 직교 투영, {r}_p

{r}_p 형식의 다각형은 정점과 가장자리 수가 같다. 그들은 또한 자기 이중적이다.

₃{3}₃ 또는 , 검정색에 8개의 꼭지점, 빨간색과 파란색에^[16] 3개의 3개의 색상이 2세트 들어 있음
24개의 꼭지점과 24개의 3개의 3개 세트가 3개의 색상 세트로 표시된 ₃{4},₃ 또는 , 한 세트가^[17] 채워짐
4가지 색상^[17] 세트로 표시된 24개의 꼭지점 및 24개의 4개의 4-세로 구성된 ₄{3},₄ 또는 ,
₃{₃5}, 또는 , 정점 120개 및 3-점^[18] 120개
정점이 120개이고 5개의^[19] 정점이 120개₅ 있는 {3}₅ 또는 ,

일반 복합 폴리토페스

일반적으로 일반 복합 폴리토프는 대칭[z₁][_qz₂][_rz₃]…_s 또는 Coxeter 다이어그램 …으로 Coxeter에 의해 {z₁}{_qz₂₃}…_r_s로 표현된다.^[20]

모든 차원에서 발생하는 일반 복합 폴리토페스의 무한 계열이 존재하며, 실제 공간에서 하이퍼큐브와 크로스 폴리토페를 일반화한다. 셰퍼드(Shephard)의 "일반화된 정형외과"는 하이퍼큐브(hypercube)를 일반화한다. γ^p
_n = {4}{₂3}₂₂ …{3}₂ 및 다이어그램 …이 주는 기호를 가지고 있다. 그것의 대칭군에는 [4][₂3]…[₂₂3];₂ 셰퍼드–에 도표가 있다.Todd 분류, 이것은 서명된 순열 매트릭스를 일반화하는 그룹 G(p, 1, n)이다. 그것의 이중 일반 폴리토프인 "일반화된 교차 폴리토프"는 기호 β^p
_n = {3}{₂3}…{₂₂4}_p와 다이어그램 …으로 표현된다.^[21]

$\mathbb {C} ^{1}$ $\mathbb {C} ^{1}$ ${\$ 의 1차원 일반 복합 폴리토프는, p 정점이 있는 것으로 표현되며 $\mathbb {C} ^{1}$ , 실제 표현은 일반 폴리곤, {p}. Coxeter는 또한 1차원 일반화된 하이퍼큐브 또는 교차 폴리토프로서 기호 γ^p
₁ 또는 β를^p
₁ 부여한다. 그것의 대칭은 [] 또는 , 순서 p의 순환 그룹이다. 상위 폴리토프에서 {} 또는 p-에지 요소를 나타내며, 2-에지, {} 또는 는 두 꼭지점 사이의 일반적인 실제 에지를 나타낸다.^[21]

이중 복합 폴리토프는 n-폴리토프의 k 및 (n-1-k) 요소들을 교환하여 구성된다. 예를 들어, 이중 복합 폴리곤은 각 에지를 중심으로 정점을 가지며, 새로운 에지는 이전 정점을 중심으로 한다. v-valance 정점은 새로운 v-edge를 생성하고 e-edge는 e-valance 정점이 된다.^[22] 일반 복합 폴리토프의 이중에는 반전된 기호가 있다. 대칭 기호가 있는 일반 복합 폴리토프, 즉 {q},_p {q}{_rq},_p {q}{_rs}{_rq}},_p 등은 자가 이중이다.

일반복합다면체 열거

어떤 그룹은 그룹 주문과 반사적인 부분군 관계와 함께 셰퍼드 그룹 3위에 랭크된다.

Coxeter는 R $\mathbb {R} ^{3}$ ${\$ 에 5개의 플라톤 고형분을 포함하여 $\mathbb {C} ^{3}$ $\mathbb {C} ^{3}$ 정규 복합 폴리헤드라의 목록을 열거했다 $\mathbb {R} ^{3}$ ^[23]

일반 복합 다면체, {n₁}{_qn₂}_r 또는 에 면, 가장자리 및 꼭지점이 있다.

복합 일반 다면체 {n₁}{_qn₂}_r는 g₁ = 순서([_pn₁])_q와₂ g = 순서([_qn₂])_r가 모두 유한해야 한다.

g = 순서([_pn₁][_qn₂]])_r를 지정하면 정점의 수는 g/g이고₂ 면의 수는₁ g/g이다. 가장자리 수는 g/pr이다.

공간	그룹	주문	콕시터 수	폴리곤	정점	가장자리		얼굴		꼭지점 형상을 나타내다	반 오스 다각형	메모들
$\mathb{R} ^{3}$	G(1,1,3) ₂[3]₂[3]₂ = [3,3]	24	4	α₃ = ₂{3}₂{3}₂ = {3,3}	4	6	{}	4	{3}	{3}	없는	리얼 사면체 와 같다
$\mathb{R} ^{3}$	G₂₃ ₂[3]₂[5]₂ = [3,5]	120	10	₂{3}₂{5}₂ = {3,5}	12	30	{}	20	{3}	{5}	없는	리얼 이코사면체
$\mathb{R} ^{3}$	G₂₃ ₂[3]₂[5]₂ = [3,5]	120	10	₂{5}₂{3}₂ = {5,3}	20	30	{}	12	{5}	{3}	없는	리얼 도데카헤드론
$\mathb{R} ^{3}$	G(2,1,3) ₂[3]₂[4]₂ = [3,4]	48	6	β² ₃ = β₃ = {3,4}	6	12	{}	8	{3}	{4}	{4}	리얼 옥타헤드론 {}+{}+{}}과(와) 같음, 주문 8 와 동일 주문 24
$\mathb{R} ^{3}$	G(2,1,3) ₂[3]₂[4]₂ = [3,4]	48	6	γ² ₃ = γ₃ = {4,3}	8	12	{}	6	{4}	{3}	없는	리얼 큐브 {}×{}×{}×{} 또는
$\mathb{C} ^{3}$	G(p,1,3) ₂[3]₂[4]_p p=2,3,4,...	6p³	3p	β^p ₃ = ₂{3}₂{4}_p	3p	3p²	{}	p³	{3}	₂{4}_p	₂{4}_p	일반화 팔면체 {}+{}+{}}_p_p과(와) 같음 p 주문³ 와 동일, 주문 6p²
$\mathb{C} ^{3}$	G(p,1,3) ₂[3]₂[4]_p p=2,3,4,...	6p³	3p	γ^p ₃ = _p{4}₂{3}₂	p³	3p²	_p{}	3p	_p{4}₂	{3}	없는	일반화 큐브 {}×{}×{}×{}_p_p 또는
$\mathb{C} ^{3}$	G(3,1,3) ₂[3]₂[4]₃	162	9	β³ ₃ = ₂{3}₂{4}₃	9	27	{}	27	{3}	₂{4}₃	₂{4}₃	{}+{}+{}}₃₃과(와) 같음, 주문 27 와 동일 주문 54
$\mathb{C} ^{3}$	G(3,1,3) ₂[3]₂[4]₃	162	9	γ³ ₃ = ₃{4}₂{3}₂	27	27	₃{}	9	₃{4}₂	{3}	없는	{}×{}×{}×{}₃₃ 또는
$\mathb{C} ^{3}$	G(4,1,3) ₂[3]₂[4]₄	384	12	β⁴ ₃ = ₂{3}₂{4}₄	12	48	{}	64	{3}	₂{4}₄	₂{4}₄	{}+{}+{}}₄₄과(와) 같음, 주문 64 와 동일, 주문 96
$\mathb{C} ^{3}$	G(4,1,3) ₂[3]₂[4]₄	384	12	γ⁴ ₃ = ₄{4}₂{3}₂	64	48	₄{}	12	₄{4}₂	{3}	없는	{}×{}×{}×{}₄₄ 또는
$\mathb{C} ^{3}$	G(5,1,3) ₂[3]₂[4]₅	750	15	β⁵ ₃ = ₂{3}₂{4}₅	15	75	{}	125	{3}	₂{4}₅	₂{4}₅	{}+{}+{}}₅₅과(와) 같음, 주문 125 와 동일, 주문 150
$\mathb{C} ^{3}$	G(5,1,3) ₂[3]₂[4]₅	750	15	γ⁵ ₃ = ₅{4}₂{3}₂	125	75	₅{}	15	₅{4}₂	{3}	없는	{}×{}×{}×{}₅₅ 또는
$\mathb{C} ^{3}$	G(6,1,3) ₂[3]₂[4]₆	1296	18	β⁶ ₃ = ₂{3}₂{4}₆	36	108	{}	216	{3}	₂{4}₆	₂{4}₆	{}+{}+{}},₆₆ 주문 216과 동일 와 동일 주문 216
$\mathb{C} ^{3}$	G(6,1,3) ₂[3]₂[4]₆	1296	18	γ⁶ ₃ = ₆{4}₂{3}₂	216	108	₆{}	18	₆{4}₂	{3}	없는	{}×{}×{}×{}₆₆ 또는
$\mathb{C} ^{3}$	G₂₅ ₃[3]₃[3]₃	648	9	₃{3}₃{3}₃	27	72	₃{}	27	₃{3}₃	₃{3}₃	₃{4}₂	와 같다. $\mathbb {R} ^{6}$ $\mathbb {R} ^{6}$ ${\$ 표현 $\mathbb {R} ^{6}$ 2로₂₁ 표시 헤시안 다면체
	G₂₆ ₂[4]₃[3]₃	1296	18	₂{4}₃{3}₃	54	216	{}	72	₂{4}₃	₃{3}₃	{6}
	G₂₆ ₂[4]₃[3]₃	1296	18	₃{3}₃{4}₂	72	216	₃{}	54	₃{3}₃	₃{4}₂	₃{4}₃	와 같다 $\mathbb {R} ^{6}$ $\mathbb {R} ^{6}$ ${\$ 표현 $\mathbb {R} ^{6}$ 1로₂₂ 표시

일반 복합 다면체의 시각화

복합 다면체의 2D 직교 투영, {s}{_tr}_r

실제 {3,3} 또는 정점 4개, 가장자리 6개 및 면 4개
₃{3}{₃3},₃ 또는 는 정점이 27개, 3각 72개, 얼굴이 27개로, 한 얼굴이 파란색으로 강조 표시되어 있다.^[25]
₂{4}{₃3}₃은(는) 정점 54개, 단순 가장자리 216개, 면 72개를 가지며, 한 면은 파란색으로 강조 표시되어 있다.^[26]
₃{3}{₃4},₂ 또는 는 정점이 72개, 정점이 216개, 정점이 54개 있으며, 한 얼굴은 파란색으로 강조 표시되어 있다.^[27]

일반화옥타헤드라

일반화된 옥타헤드라는 규칙적인 구조를 가지고 있고, quasiregular 형식을 가지고 있다. 모든 요소들은 단순하다.

정점이 6개, 가장자리 12개 및 면 8개인 실제 {3,4} 또는 .
₂{3}{₂4},₃ 또는 , 정점 9개, 가장자리 27개 및 면 27개
정점 12개, 가장자리 48개₂, 면 64개인 {3}{₂4}₄ 또는 .
정점 15개, 가장자리 75개 및 면 125개인₂ {3}{₂4}₅ 또는 .
정점 18개, 가장자리 108개 및 면 216개인 {3₂}{₂4}₆ 또는 .
정점이 21개, 가장자리 147개, 면 343개로 구성된 {3₂}{₂4},₇ 또는 ,
24개의 꼭지점, 192개의 가장자리 및 512개의 면으로 구성된₂ {3}{₂4}₈ 또는 .
₂{3}{₂4},₉ 또는 , 27개의 꼭지점, 243개의 가장자리 및 729개의 면
정점 30개,₂ 가장자리 300개₂, 면 1000개인 {3}{4}₁₀ 또는 .

일반화 큐브

일반화된 정육면체는 p-곤 1-폴리토프 3개로 구성된 제품인 as와 prismatic 구조를 가지고 있다. 원소는 더 낮은 차원의 일반화된 큐브다.

실제 {4,3} 또는 정점 8개, 가장자리 12개 및 면 6개
₃{4}{₂3}₂ 또는 정점 27개, 3개 및 9개^[25] 면
정점이 64개, 가장자리 48개 및 면 12개인₄ {4}{₂3}₂ 또는 .
정점 125개, 가장자리 75개, 면 15개인₅ {4}{₂3}₂ 또는 .
₆{4}{₂3},₂ 또는 , 정점 216개, 가장자리 108개, 면 18개
정점 343개, 가장자리 147개, 면 21개인₇ {4}{₂3}₂ 또는 .
정점이₈ 512개, 가장자리 192개 및 면 24개인 {₂4}{3}₂ 또는 .
정점 729개, 가장자리 243개 및 면 27개인₉ {4}{₂3}₂ 또는 .
정점 1000개, 가장자리 300개 및 면 30개인₁₀ {4}{₂3}₂ 또는 ,

일반복합 4폴리토페의 열거

Coxeter는 R $\mathbb {R} ^{4}$ ${\$ $displaystyle \mathb {C} ^4}$ 에 있는 6개의 볼록 정규 4-폴리탑을 $\mathbb {C} ^{4}$ 이 비별 정규 4-폴리탑 목록을 C 4 ${\$ $displaystyle \mathb {R} ^4}$ 에 열거했다 $\mathbb {R} ^{4}$ ^[23]

공간	그룹	주문	콕시터 번호를 붙이다	폴리토프	정점	가장자리	얼굴	세포	반 오스 다각형	메모들
$\mathb{R} ^{4}$	G(1,1,4) ₂[3]₂[3]₂[3]₂ = [3,3,3]	120	5	α₄ = ₂{3}₂{3}₂{3}₂ = {3,3,3}	5	10 {}	10 {3}	5 {3,3}	없는	실제 5-셀(단순)
$\mathb{R} ^{4}$	G₂₈ ₂[3]₂[4]₂[3]₂ = [3,4,3]	1152	12	₂{3}₂{4}₂{3}₂ = {3,4,3}	24	96 {}	96 {3}	24 {3,4}	{6}	리얼 24셀
	G₃₀ ₂[3]₂[3]₂[5]₂ = [3,3,5]	14400	30	₂{3}₂{3}₂{5}₂ = {3,3,5}	120	720 {}	1200 {3}	600 {3,3}	{10}	리얼 600 셀
	G₃₀ ₂[3]₂[3]₂[5]₂ = [3,3,5]	14400	30	₂{5}₂{3}₂{3}₂ = {5,3,3}	600	1200 {}	720 {5}	120 {5,3}	{10}	리얼 120 셀
$\mathb{R} ^{4}$	G(2,1,4) ₂[3]₂[3]₂[4]_p =[3,3,4]	384	8	β² ₄ = β₄ = {3,3,4}	8	24 {}	32 {3}	16 {3,3}	{4}	리얼 16셀 와 동일 주문 192
$\mathb{R} ^{4}$	G(2,1,4) ₂[3]₂[3]₂[4]_p =[3,3,4]	384	8	γ² ₄ = γ₄ = {4,3,3}	16	32 {}	24 {4}	8 {4,3}	없는	리얼 테세락트 {}⁴ 또는 , 주문 16과 동일
$\mathb{C} ^{4}$	G(p,1,4) ₂[3]₂[3]₂[4]_p p=2,3,4,...	24p⁴	4p	β^p ₄ = ₂{3}₂{3}₂{4}_p	4p	6p² {}	4p³ {3}	p⁴ {3,3}	₂{4}_p	일반화 4정형 와 동일 주문 24p³
$\mathb{C} ^{4}$	G(p,1,4) ₂[3]₂[3]₂[4]_p p=2,3,4,...	24p⁴	4p	γ^p ₄ = _p{4}₂{3}₂{3}₂	p⁴	4p³ _p{}	6p² _p{4}₂	4p _p{4}₂{3}₂	없는	일반화 큐브 {}⁴ 또는 , 오더 p와⁴ 동일
$\mathb{C} ^{4}$	G(3,1,4) ₂[3]₂[3]₂[4]₃	1944	12	β³ ₄ = ₂{3}₂{3}₂{4}₃	12	54 {}	108 {3}	81 {3,3}	₂{4}₃	일반화 4정형 와 동일 주문 648
$\mathb{C} ^{4}$	G(3,1,4) ₂[3]₂[3]₂[4]₃	1944	12	γ³ ₄ = ₃{4}₂{3}₂{3}₂	81	108 ₃{}	54 ₃{4}₂	12 ₃{4}₂{3}₂	없는	{}⁴ 또는 , 주문 81과 동일
$\mathb{C} ^{4}$	G(4,1,4) ₂[3]₂[3]₂[4]₄	6144	16	β⁴ ₄ = ₂{3}₂{3}₂{4}₄	16	96 {}	256 {3}	64 {3,3}	₂{4}₄	와 동일, 주문 1536
$\mathb{C} ^{4}$	G(4,1,4) ₂[3]₂[3]₂[4]₄	6144	16	γ⁴ ₄ = ₄{4}₂{3}₂{3}₂	256	256 ₄{}	96 ₄{4}₂	16 ₄{4}₂{3}₂	없는	{}⁴ 또는 , 주문 256과 동일
$\mathb{C} ^{4}$	G(5,1,4) ₂[3]₂[3]₂[4]₅	15000	20	β⁵ ₄ = ₂{3}₂{3}₂{4}₅	20	150 {}	500 {3}	625 {3,3}	₂{4}₅	와 동일, 주문 3000
$\mathb{C} ^{4}$	G(5,1,4) ₂[3]₂[3]₂[4]₅	15000	20	γ⁵ ₄ = ₅{4}₂{3}₂{3}₂	625	500 ₅{}	150 ₅{4}₂	20 ₅{4}₂{3}₂	없는	{}⁴과(와) 동일하거나 ,
$\mathb{C} ^{4}$	G(6,1,4) ₂[3]₂[3]₂[4]₆	31104	24	β⁶ ₄ = ₂{3}₂{3}₂{4}₆	24	216 {}	864 {3}	1296 {3,3}	₂{4}₆	와 동일 주문 5184
$\mathb{C} ^{4}$	G(6,1,4) ₂[3]₂[3]₂[4]₆	31104	24	γ⁶ ₄ = ₆{4}₂{3}₂{3}₂	1296	864 ₆{}	216 ₆{4}₂	24 ₆{4}₂{3}₂	없는	{}⁴ 또는 , 주문 1296과 동일
$\mathb{C} ^{4}$	G₃₂ ₃[3]₃[3]₃[3]₃	155520	30	₃{3}₃{3}₃{3}₃	240	2160 ₃{}	2160 ₃{3}₃	240 ₃{3}₃{3}₃	₃{4}₃	웨이팅 폴리토프 $\mathbb {R} ^{8}$ $\mathbb {R} ^{8}$ ${\$ 표현 $\mathbb {R} ^{8}$ 4로₂₁ 표시

일반 복합 4폴리탑의 시각화

실제 {3,3}은(는) 5개의 꼭지점, 10개의 가장자리, 10개의 면, 10개의 {3}개의 면, 5개의 {3,3}개의 셀을 가지고 있었다.
실제 {3,4,3}은(는) 꼭지점 24개, 가장자리 96개, 면 96개, 셀 24개 {3,4}개였습니다.
실제 {5,3,3}은(는) 600개의 꼭지점, 1200개의 가장자리, 720개의 {5}개의 면, 120개의 {5,3}개의 셀을 가지고 있었다.
실제 {3,5,} 은 120 정점, 720 엣지, 1200 {3} 면, 600 {3,3} 셀을 가지고 있었다.
와이트팅 폴리토프(Witing polytope, )는 정점 240, 3-edge 2160, 얼굴 2160 3{3}3, 셀 240 3{3}3을 가지고 있다.

일반화 4형식

일반화된 4정형인 사람은 as와 quasiregular의 형태가 규칙적인 구조를 가지고 있다. 모든 원소는 단순하다.

8개의 꼭지점, 24개의 가장자리, 32개의 면 및 16개의 셀이 있는 실제 {3,3,4} 또는 .
₂{3}{₂3}{₂4}₃ 또는 12개의 꼭지점, 54개의 가장자리, 108개의 면 및 81개의 셀이 있는 ,
₂{3}{₂3}{₂4}₄ 또는 , 정점 16개, 가장자리 96개, 면 256개, 셀 256개
₂{3}{₂3}{₂4}₅ 또는 , 정점 20개, 가장자리 150개, 면 500개, 셀 625개
₂{3}{₂3}{₂4}₆ 또는 , 정점 24개, 가장자리 216개, 면 864개, 셀 1296개
₂{3}{₂3}{₂4}₇ 또는 , 정점 28개, 가장자리 294개, 면 1372개, 셀 2401개
₂{3}{₂3}{₂4},₈ 또는 , 정점 32개, 가장자리 384개, 면 2048개, 셀 4096개
₂{3}{₂3}{₂4}₉ 또는 , 정점 36개, 가장자리 486개, 면 2916개, 셀 6561개
₂{3}{₂3}{₂4}₁₀ 또는 , 정점 40개, 가장자리 600개, 면 4000개, 셀 10000개

일반화 4-Cube

일반화된 큐빅은 4개의 p-gonal 1-폴리탑의 제품인 p-gonal 1-polytopes와 같은 프리즘 구조로 정기적인 구조를 가지고 있다. 원소는 더 낮은 차원의 일반화된 큐브다.

16개의 꼭지점, 32개의 가장자리, 24개의 면 및 8개의 셀이 있는 실제 {4,3,3} 또는 .
₃{4}{₂3}{₂3}₂ 또는 , 정점 81개, 가장자리 108개, 면 54개 및 셀 12개 포함
₄{4}{₂3}{₂3}₂ 또는 , 정점 256, 가장자리 96, 면 96, 셀 16개 포함
₅{4}{₂3}{₂3}₂ 또는 , 정점 625개, 가장자리 500개, 면 150개, 셀 20개 포함
₆{4}{₂3}{₂3},₂ 또는 1296개의 꼭지점, 864개의 가장자리, 216개의 면, 24개의 셀이 있는 ,
₇{4}{₂3}{₂3},₂ 또는 , 정점 2401개, 가장자리 1372개, 면 294개, 셀 28개
₈{4}{₂3}{₂3}₂ 또는 , 정점 4096개, 가장자리 2048개, 면 384개, 셀 32개 포함
₉{4}{₂3}{₂3},₂ 또는 , 정점 6561, 가장자리 2916, 면 486, 셀 36개
₁₀{4}{₂3}{₂3}₂ 또는 10000 꼭지점, 4000 엣지, 600 면 및 40 셀이 있는 ,

일반복합 5폴리탑 열거

$\mathbb {C} ^{5}$ $\mathbb {C} ^{5}$ ${\$ 이상의 $\mathbb {C} ^{5}$ 정규 복합 5폴리탑은 실제 심플렉스, 일반화된 하이퍼큐브, 직교 등 3개 계열로 존재한다.

공간	그룹	주문	폴리토프	정점	가장자리	얼굴	세포	4시 15분	반 오스 다각형	메모들
$\mathb{R} ^{5}$	G(1,1,5) = [3,3,3,3]	720	α₅ = {3,3,3,3}	6	15 {}	20 {3}	15 {3,3}	6 {3,3,3}	없는	리얼 5심플렉스
$\mathb{R} ^{5}$	G(2,1,5) =[3,3,3,4]	3840	β² ₅ = β₅ = {3,3,3,4}	10	40 {}	80 {3}	80 {3,3}	32 {3,3,3}	{4}	리얼 5정형 와 동일, 순서 1920
$\mathb{R} ^{5}$	G(2,1,5) =[3,3,3,4]	3840	γ² ₅ = γ₅ = {4,3,3,3}	32	80 {}	80 {4}	40 {4,3}	10 {4,3,3}	없는	리얼 5큐브 {}⁵ 또는 , 주문 32와 동일
$\mathb{C} ^{5}$	G(p,1,5) ₂[3]₂[3]₂[3]₂[4]_p	120펜스⁵	β^p ₅ = ₂{3}₂{3}₂{3}₂{4}_p	5p	10p² {}	10p³ {3}	5p⁴ {3,3}	p⁵ {3,3,3}	₂{4}_p	일반화 5정형 와 동일, 120p⁴ 주문
$\mathb{C} ^{5}$	G(p,1,5) ₂[3]₂[3]₂[3]₂[4]_p	120펜스⁵	γ^p ₅ = _p{4}₂{3}₂{3}₂{3}₂	p⁵	5p⁴ _p{}	10p³ _p{4}₂	10p² _p{4}₂{3}₂	5p _p{4}₂{3}₂{3}₂	없는	일반화 5-큐브 {}⁵ 또는 , 오더 p와⁵ 동일
$\mathb{C} ^{5}$	G(3,1,5) ₂[3]₂[3]₂[3]₂[4]₃	29160	β³ ₅ = ₂{3}₂{3}₂{3}₂{4}₃	15	90 {}	270 {3}	405 {3,3}	243 {3,3,3}	₂{4}₃	와 동일, 주문 9720
$\mathb{C} ^{5}$	G(3,1,5) ₂[3]₂[3]₂[3]₂[4]₃	29160	γ³ ₅ = ₃{4}₂{3}₂{3}₂{3}₂	243	405 ₃{}	270 ₃{4}₂	90 ₃{4}₂{3}₂	15 ₃{4}₂{3}₂{3}₂	없는	{}⁵ 또는 , 주문 243과 동일
$\mathb{C} ^{5}$	G(4,1,5) ₂[3]₂[3]₂[3]₂[4]₄	122880	β⁴ ₅ = ₂{3}₂{3}₂{3}₂{4}₄	20	160 {}	640 {3}	1280 {3,3}	1024 {3,3,3}	₂{4}₄	와 동일, 주문 30720
$\mathb{C} ^{5}$	G(4,1,5) ₂[3]₂[3]₂[3]₂[4]₄	122880	γ⁴ ₅ = ₄{4}₂{3}₂{3}₂{3}₂	1024	1280 ₄{}	640 ₄{4}₂	160 ₄{4}₂{3}₂	20 ₄{4}₂{3}₂{3}₂	없는	{}⁵ 또는 , 주문 1024와 동일
$\mathb{C} ^{5}$	G(5,1,5) ₂[3]₂[3]₂[3]₂[4]₅	375000	β⁵ ₅ = ₂{3}₂{3}₂{3}₂{5}₅	25	250 {}	1250 {3}	3125 {3,3}	3125 {3,3,3}	₂{5}₅	와 동일, 주문 75000
$\mathb{C} ^{5}$	G(5,1,5) ₂[3]₂[3]₂[3]₂[4]₅	375000	γ⁵ ₅ = ₅{4}₂{3}₂{3}₂{3}₂	3125	3125 ₅{}	1250 ₅{5}₂	250 ₅{5}₂{3}₂	25 ₅{4}₂{3}₂{3}₂	없는	{}⁵ 또는 , 주문 3125와 동일
$\mathb{C} ^{5}$	G(6,1,5) ₂[3]₂[3]₂[3]₂[4]₆	933210	β⁶ ₅ = ₂{3}₂{3}₂{3}₂{4}₆	30	360 {}	2160 {3}	6480 {3,3}	7776 {3,3,3}	₂{4}₆	와 동일, 주문 155520
$\mathb{C} ^{5}$	G(6,1,5) ₂[3]₂[3]₂[3]₂[4]₆	933210	γ⁶ ₅ = ₆{4}₂{3}₂{3}₂{3}₂	7776	6480 ₆{}	2160 ₆{4}₂	360 ₆{4}₂{3}₂	30 ₆{4}₂{3}₂{3}₂	없는	{}⁵ 또는 , 주문 7776과 동일

일반 복합 5폴리탑의 시각화

일반화 5형식

일반화된 5형식인 5형식인 경우 정기적인 구조를 가지고 있으며, 4형식인 경우 모든 원소는 단순하다.

정점 10개, 가장자리 40개, 면 80개, 셀 80개, 4-페이스를 가진 실제 {3,3,4}.
₂{3}{₂3}{₂3}{3}{₂4},₃ , 정점 15개, 가장자리 90개, 면 270개, 셀 405개, 4개 243개
₂{3}{₂3}{₂3}{3}{₂4},₄ , 정점 20개, 가장자리 160개, 면 640개, 셀 1280개 및 4-118개.
₂{3}{₂3}{₂3}{3}{₂4},₅ , 정점 25개, 가장자리 250개, 면 1250개, 셀 3125개, 4개 3125개
₂{3}{₂3}{₂3}{3}{₂4},₆ 30개의 꼭지점, 360개의 가장자리, 2160개의 면, 6480개의 셀, 7776개의 4-118이 있음
₂{3}{₂3}{₂3}{3}{₂4},₇ , 35정점, 490정점, 3430면, 12005셀, 16807 4-118
₂{3}{₂3}{₂3}{₂3}{4},₈ , 정점 40개, 가장자리 640개, 면 5120개, 셀 20480개, 셀 32768개 4개
₂{3}{₂3}{₂3}{₂4},₉ , 정점 45개, 가장자리 810개, 면 7290개, 셀 32805개, 셀 59049 4개
₂{3}{₂3}{₂3}{3}{₂4},₁₀ 50개의 꼭지점, 1000개의 가장자리, 10000개의 면, 50000개의 셀, 100000개의 4-모듈이 있음

일반화 5-Cube

일반화된 5-Cube는 5개의 p-곤 1-폴리탑의 제품인 프리즘 구조로서 정기적인 구조를 가지고 있다. 원소는 더 낮은 차원의 일반화된 큐브다.

정점 32개, 가장자리 80개, 면 80개, 셀 40개 및 4-페이스를 가진 실제 {4,3,3}
₃{4}{₂3}{₂3}{₂3}{3}{3}}₂ , 정점 243개, 가장자리 405개, 면 270개, 셀 90개, 4-105개 등.
₄{4}{₂3}{₂3}{₂3}{3}{3}}₂ , 정점 1024개, 가장자리 1280개, 면 640개, 셀 160개, 4개 20개
₅{4}{₂3}{₂3}{₂3}{3}{3}}₂ , 정점 3125, 가장자리 3125, 면 1250, 셀 250, 4개 25개
₆{4}{₂3}{₂3}{₂3}{3}{3}}₂ , 정점 7776, 가장자리 6480, 면 2160, 셀 360, 4-1330개

일반복합 6폴리탑 열거

공간	그룹	주문	폴리토프	정점	가장자리	얼굴	세포	4시 15분	5시 15분	반 오스 다각형	메모들
$\mathb{R} ^{6}$	G(1,1,6) = [3,3,3,3,3]	720	α₆ = {3,3,3,3,3}	7	21 {}	35 {3}	35 {3,3}	21 {3,3,3}	7 {3,3,3,3}	없는	리얼 6심플렉스
$\mathb{R} ^{6}$	G(2,1,6) [3,3,3,4]	46080	β² ₆ = β₆ = {3,3,3,4}	12	60 {}	160 {3}	240 {3,3}	192 {3,3,3}	64 {3,3,3,3}	{4}	리얼 6정형 와 동일 주문 23040
$\mathb{R} ^{6}$	G(2,1,6) [3,3,3,4]	46080	γ² ₆ = γ₆ = {4,3,3,3}	64	192 {}	240 {4}	160 {4,3}	60 {4,3,3}	12 {4,3,3,3}	없는	리얼 6-큐브 {}⁶ 또는 , 주문 64와 동일
$\mathb{C} ^{6}$	G(p,1,6) ₂[3]₂[3]₂[3]₂[4]_p	720p⁶	β^p ₆ = ₂{3}₂{3}₂{3}₂{4}_p	6p	15p² {}	20p³ {3}	15p⁴ {3,3}	6p⁵ {3,3,3}	p⁶ {3,3,3,3}	₂{4}_p	일반화 6정형식 와 동일 주문 720p⁵
$\mathb{C} ^{6}$	G(p,1,6) ₂[3]₂[3]₂[3]₂[4]_p	720p⁶	γ^p ₆ = _p{4}₂{3}₂{3}₂{3}₂	p⁶	6p⁵ _p{}	15p⁴ _p{4}₂	20p³ _p{4}₂{3}₂	15p² _p{4}₂{3}₂{3}₂	6p _p{4}₂{3}₂{3}₂{3}₂	없는	일반화 6-큐브 {}⁶ 또는 , 오더 p와⁶ 동일

일반 복합 6폴리탑의 시각화

일반화 6형식

일반화된 6정형인 사람은 as와 quasiregular의 형태가 규칙적인 구조를 가지고 있다. 모든 원소는 단순하다.

실제 {3,3,3,3,4}, 12개의 꼭지점, 60개의 가장자리, 160개의 면, 240개의 셀, 192개의 4-패스, 64개의 5-패스가 있음
₂{3}{₂3}{₂3}{₂3}{3}{₂4}₃ , 정점 18개, 가장자리 135개, 면 540개, 셀 1215개, 셀 1458 4개, 5개, 729개.
₂{3}{₂3}{₂3}{₂3}{3}{₂4}₄ , 정점 24개, 가장자리 240개, 면 1280개, 셀 3840개, 셀 6144개, 5개, 4096개.
₂{3}{₂3}{₂3}{₂3}{3}{₂3}{₅4}, , 정점 30개, 가장자리 375개, 면 2500개, 셀 9375개, 셀 18750개, 5개, 5개, 15625개
₂{3}{₂3}{₂3}{₂3}{3}{₂4},₆ 36 꼭지점, 540 엣지, 4320 면, 19440 셀, 46656 4-14, 46656 5-136 .
₂{3}{₂3}{₂3}{₂3}{3}{₂4}₇ , 정점 42개, 가장자리 735개, 면 6860개, 셀 36015개, 셀 100842개, 4개, 117649 5개.
₂{3}{₂3}{₂3}{₂3}{3}{₂4}₈ , 정점 48개, 가장자리 960개, 면 10240개, 셀 61440개, 셀 196608 4개, 5개, 262144개.
₂{3}{₂3}{₂3}{₂3}{3}{₂3}{4},₉ 54 꼭지점, 1215 엣지, 14580 면, 98415 셀, 354294 4-115, 531441 5-141
₂{3}{₂3}{₂3}{₂3}{3}{₂4},₁₀ 60 꼭지점, 1500 가장자리, 20000면, 150000면, 150000셀, 600000 4개, 1000000 5개.

일반화 6-Cube

일반화된 6-Cube는 p-gonal 1-polytopes 6개의 제품인 p-gonal 1-polytopes와 같이 규칙적인 구조를 가지고 있다. 원소는 더 낮은 차원의 일반화된 큐브다.

64개의 꼭지점, 192개의 가장자리, 240개의 면, 160개의 셀, 60개의 4-페이스, 12개의 5-페이스를 가진 실제 {3,3,3,3,4}.
₃{4}{₂3}{₂3}{₂3}{3}{₂3}{3}}₂ , 정점 729개, 가장자리 1458개, 면 1215개, 셀 540개, 4개, 5개, 18개 5개.
₄{4}{₂3}{₂3}{₂3}{3}{₂3}{3}{3}}₂ , 정점 4096개, 가장자리 6144개, 면 3840개, 셀 1280개, 셀 240개, 5개 24개가 있음
₅{4}{₂3}{₂3}{₂3}{3}{₂3}{3}{3}}₂ , 15625 정점, 18750 엣지, 9375 면, 2500 셀, 375 4-11, 30 5-118을 사용함

일반복합아페이로톱의 열거

Coxeter는 이 비별난 일반 콤플렉스 애피로토페스 또는 허니컴의 목록을 열거했다.^[28]

각 차원에 대해 $\mathbb {C} ^{n}$ 로^p,r
_n+1 상징되는 12개의 아페이로탑이 C $\mathbb {C} ^{n}$ ${\$ { $C} ^{n$ 또는 $\mathbb {R} ^{n}$ {\ $displaystyle \mathb {R} ^$ n} ^n $}($ p $\mathbb {R} ^{n}$ =q=2)에 존재한다. Coxeter는 이러한 일반화된 큐빅 벌집들을 n>2라고 부른다.^[29]

각 항목에는 다음과 같이 주어진 비례 요소 카운트가 있다.

k-162 =

{n \choose k}p^{n-k}r^{k}

(

{n \choose k}p^{n-k}r^{k}

k

{n \choose k}p^{n-k}r^{k}

)

{n \choose k}p^{n-k}r^{k}

-

{n \choose k}p^{n-k}r^{k}

k

{n \choose k}p^{n-k}r^{k}

{n \choose k}p^{n-k}r^{k}

{\

\

p^{n-k}r^{k

여기서

{n \choose m}={\frac {n!}{m!\,(n-m)!}}

(

{n \choose m}={\frac {n!}{m!\,(n-m)!}}

{n \choose m}={\frac {n!}{m!\,(n-m)!}}

=

{n \choose m}={\frac {n!}{m!\,(n-m)!}}

- m

{\

n

\선택

m

}={\frac

{

n!

}{{m!\, (n-m)!

}}}

과

{n \choose m}={\frac {n!}{m!\,(n-m)!}}

n!은 n의 인자를 나타낸다.

일반복합1폴리탑

유일한 정기적인 복합 1폴리토프는 {}, 또는 . 실제 표현은 afeirogon, { {}, 또는 .

일반복합아페이로곤스

아페이로겐 셰퍼드 그룹의 일부

11개의 복잡한 아페이로곤 {q}_r에 엣지 인테리어가 연한 청색으로, 하나의 꼭지점 주변의 가장자리가 개별적으로 색칠된다. 꼭지점은 작은 검은색 정사각형으로 표시된다. 가장자리는 p-side 정규 다각형으로 보이며 꼭지점은 r-곤골이다.

quasiregular afeirogon은 두 개의 일반적인 afeirogon과, 여기서 파란색과 분홍색 가장자리가 보이는 혼합물이다.

q가 홀수이기 때문에 엣지 색상이 하나만 있어 이중 커버가 된다.

2위 콤플렉스 아페이로곤은 대칭[q]_r을 가지고 있다. 여기서 1/p + 2/q + 1/r = 1. $콕시터$ 는 q^p,r
₂ = 2 $/(1 -$ ( $p$ + r $)/ pr)$ ^[30]를 만족시키기 위해 Δ로 표현한다.

다음과 같은 8가지 솔루션이 있다.

₂[∞]₂	₃[12]₂	₄[8]₂	₆[6]₂	₃[6]₃	₆[4]₃	₄[4]₄	₆[3]₆

홀수 q와 불평등한 p와 r의 두 가지 제외된 솔루션이 있다: [5]와 [3],₂₄ 또는 .

일반 복합 에이페이로곤 {q}_r에는 p-edge와 r-곤 정점 수치가 있다. {q}_r의 이중 아페이로곤은 {q}_p이다. {q}_p 형식의 아페이로곤은 자체 이중이다. [2q]₂ 형식의 그룹은 대칭[q]_p이 절반이므로 일반 아페이로곤은 quasiregular와 같다.^[31]

아간드 평면에 아페이로곤은 4개의 정점 배열을 공유할 수 있다. {q}_r 형식의 아페이로곤은 정점 배열이 {q/2,p}이다. {q}₂ 양식의 정점 배열이 r{p,q/2}이다. {4}_r 형식의 아페이로곤에는 정점 배열이 {p,r}개 있다.

아핀 노드, $\mathbb {C} ^{2}$ C $\mathbb {C} ^{2}$ ${\$ ^{ $2$ 무한 솔루션 3개가 더 있다: [2],_∞ [4],₂ [3],₃ [3], and , 및 . 첫번째는 두 번째의 지수 2 하위그룹이다. 이러한 아페이로곤의 꼭지점은 $\mathbb {C} ^{1}$ $\mathbb {C} ^{1}$ ${\$ }에 있다 $\mathbb {C} ^{1}$

2위
공간	그룹	아페이로곤	가장자리	$\mathbb {R} ^{2}$ $\mathbb {R} ^{2}$ ${\$ rep $\mathbb {R} ^{2}$ .^[32]	메모들
$\mathb{R} ^{1$	₂[∞]₂ = [∞]	δ^2,2 ₂ = {∞}	{}		리얼애페이로곤 와 같다
$\mathbb {C} ^{2}$ $\mathbb {C} ^{2}$ ${\$ $\mathbb {C} ^{2}$ / $\mathbb {C} ^{1}$ $\mathbb {C} ^{1}$ ${\$ }	_∞[4]₂	_∞{4}₂	_∞{}	{4,4}	와 같다
$\mathb{C} ^{1$	_∞[3]₃	_∞{3}₃	_∞{}	{3,6}	와 같다
$\mathb{C} ^{1$	_p[q]_r	Δ^p,r ₂ = {q}_r	_p{}
$\mathb{C} ^{1$	₃[12]₂	δ^3,2 ₂ = ₃{12}₂	₃{}	r{3,6}	와 같다
$\mathb{C} ^{1$	₃[12]₂	δ^2,3 ₂ = ₂{12}₃	{}	{6,3}
$\mathb{C} ^{1$	₃[6]₃	δ^3,3 ₂ = ₃{6}₃	₃{}	{3,6}	와 같다
$\mathb{C} ^{1$	₄[8]₂	δ^4,2 ₂ = ₄{8}₂	₄{}	{4,4}	와 같다
$\mathb{C} ^{1$	₄[8]₂	δ^2,4 ₂ = ₂{8}₄	{}	{4,4}
$\mathb{C} ^{1$	₄[4]₄	δ^4,4 ₂ = ₄{4}₄	₄{}	{4,4}	와 같다
$\mathb{C} ^{1$	₆[6]₂	δ^6,2 ₂ = ₆{6}₂	₆{}	r{3,6}	와 같다
$\mathb{C} ^{1$	₆[6]₂	δ^2,6 ₂ = ₂{6}₆	{}	{3,6}
$\mathb{C} ^{1$	₆[4]₃	δ^6,3 ₂ = ₆{4}₃	₆{}	{6,3}
$\mathb{C} ^{1$	₆[4]₃	δ^3,6 ₂ = ₃{4}₆	₃{}	{3,6}
$\mathb{C} ^{1$	₆[3]₆	δ^6,6 ₂ = ₆{3}₆	₆{}	{3,6}	와 같다

일반복합아페이로헤드라

{a}{_qb._r 8은 자가듀얼(p=r 및 a=b)이고 14개는 이중 폴리토프 쌍으로 존재한다. 3은 완전히 진짜다(p=q=r=2).

Δ^p,r
₃ 또는 {4}{₂4}{4}_r는 제품의 정규 형태인 Δ^p,r
₂ × Δ^p,r
₂ 또는 {q}_r × {q} × {q}이며,_r 여기서 q는 p와 r에서 결정된다.

p,r=2,3,4,6에 대해서는 , 및 와 동일하다. 또한 ^[33]= .

3위
공간	그룹	아페이로헤드론	꼭지점	가장자리		면		판 오스 아페이로곤	메모들
$\mathb{C} ^{3}$	₂[3]₂[4]_∞	_∞{4}₂{3}₂			_∞{}		_∞{4}₂		{}×{}×{}×{}_∞_∞ 또는 실제 표현 {4,3,4}
$\mathb{C} ^{2}$	_p[4]₂[4]_r	_p{4}₂{4}_r	p²	2pq	_p{}	r²	_p{4}₂	₂{q}_r	, p,r=2,3,4,6과 같다.
$\mathb{R} ^{2}$	[4,4]	δ^2,2 ₃ = {4,4}	4	8	{}	4	{4}	{∞}	리얼 스퀘어 타일링 or와 동일
$\mathb{C} ^{2}$	₃[4]₂[4]₂ ₃[4]₂[4]₃ ₄[4]₂[4]₂ ₄[4]₂[4]₄ ₆[4]₂[4]₂ ₆[4]₂[4]₃ ₆[4]₂[4]₆	₃{4}₂{4}₂ ₂{4}₂{4}₃ ₃{4}₂{4}₃ ₄{4}₂{4}₂ ₂{4}₂{4}₄ ₄{4}₂{4}₄ ₆{4}₂{4}₂ ₂{4}₂{4}₆ ₆{4}₂{4}₃ ₃{4}₂{4}₆ ₆{4}₂{4}₆	9 4 9 16 4 16 36 4 36 9 36	12 12 18 16 16 32 24 24 36 36 72	₃{} {} ₃{} ₄{} {} ₄{} ₆{} {} ₆{} ₃{} ₆{}	4 9 9 4 16 16 4 36 9 36 36	₃{4}₂ {4} ₃{4}₂ ₄{4}₂ {4} ₄{4}₂ ₆{4}₂ {4} ₆{4}₂ ₃{4}₂ ₆{4}₂	_p{q}_r	or와 동일 와 같다 와 같다 or와 동일 와 같다 와 같다 or와 동일 와 같다 와 같다 와 같다 와 같다

공간	그룹	아페이로헤드론	꼭지점	가장자리		면		판 오스 아페이로곤	메모들
$\mathb{C} ^{2}$	₂[4]_r[4]₂	₂{4}_r{4}₂	2		{}	2	_p{4}_2'	₂{4}_r	와 동일, , r=2,3,4,6
$\mathb{R} ^{2}$	[4,4]	{4,4}	2	4	{}	2	{4}	{∞}	와 동일
$\mathb{C} ^{2}$	₂[4]₃[4]₂ ₂[4]₄[4]₂ ₂[4]₆[4]₂	₂{4}₃{4}₂ ₂{4}₄{4}₂ ₂{4}₆{4}₂	2	9 16 36	{}	2	₂{4}₃ ₂{4}₄ ₂{4}₆	₂{q}_r	와 동일 와 동일 와 동일

공간	그룹	아페이로헤드론	꼭지점	가장자리		면		판 오스 아페이로곤	메모들
$\mathb{R} ^{2}$	₂[6]₂[3]₂ = [6,3]	{3,6}	1	3	{}	2	{3}	{∞}	리얼 삼각 타일링
$\mathb{R} ^{2}$	₂[6]₂[3]₂ = [6,3]	{6,3}	2	3	{}	1	{6}	없는	리얼 육각 타일링
$\mathb{C} ^{2}$	₃[4]₃[3]₃	₃{3}₃{4}₃	1	8	₃{}	3	₃{3}₃	₃{4}₆	와 같다
$\mathb{C} ^{2}$	₃[4]₃[3]₃	₃{4}₃{3}₃	3	8	₃{}	2	₃{4}₃	₃{12}₂
$\mathb{C} ^{2}$	₄[3]₄[3]₄	₄{3}₄{3}₄	1	6	₄{}	1	₄{3}₄	₄{4}₄	와 같은 셀프듀얼
$\mathb{C} ^{2}$	₄[3]₄[4]₂	₄{3}₄{4}₂	1	12	₄{}	3	₄{3}₄	₂{8}₄	와 같다
$\mathb{C} ^{2}$	₄[3]₄[4]₂	₂{4}₄{3}₄	3	12	{}	1	₂{4}₄	₄{4}₄

일반 콤플렉스 3-아페이로톱스

$\mathbb {C} ^{3}$ $\mathbb {C} ^{3}$ ${\$ 에 16개의 정규 콤플렉스 애피로탑이 있으며, $\mathbb {C} ^{3}$ 콕시터는 이 중 12개를 Δ로^p,r
₃ 표현하는데, q는 $q$ = $2/(1$ – (p + $r)/ pr$ 을 만족하도록 제약을 받는다 $.$ 이것들은 제품 아페이로톱으로 분해될 수도 있다: = . 첫 번째 경우는 $\mathbb {R} ^{3}$ 3 ${\$ 입방 $\mathbb {R} ^{3}$ 벌집이다.

4위
공간	그룹	3아페이로토프	가장자리	면	셀	판 오스 아페이로곤	메모들
$\mathb{C} ^{3}$	_p[4]₂[3]₂[4]_r	δ^p,r ₃ = _p{4}₂{3}₂{4}_r	_p{}	_p{4}₂	_p{4}₂{3}₂	_p{q}_r	와 같다
$\mathb{R} ^{3}$	₂[4]₂[3]₂[4]₂ =[4,3,4]	δ^2,2 ₃ = ₂{4}₂{3}₂{4}₂	{}	{4}	{4,3}		큐빅 벌집 or와 동일
$\mathb{C} ^{3}$	₃[4]₂[3]₂[4]₂	δ^3,2 ₃ = ₃{4}₂{3}₂{4}₂	₃{}	₃{4}₂	₃{4}₂{3}₂		or와 동일
$\mathb{C} ^{3}$	₃[4]₂[3]₂[4]₂	δ^2,3 ₃ = ₂{4}₂{3}₂{4}₃	{}	{4}	{4,3}		와 같다
$\mathb{C} ^{3}$	₃[4]₂[3]₂[4]₃	δ^3,3 ₃ = ₃{4}₂{3}₂{4}₃	₃{}	₃{4}₂	₃{4}₂{3}₂		와 같다
$\mathb{C} ^{3}$	₄[4]₂[3]₂[4]₂	δ^4,2 ₃ = ₄{4}₂{3}₂{4}₂	₄{}	₄{4}₂	₄{4}₂{3}₂		or와 동일
$\mathb{C} ^{3}$	₄[4]₂[3]₂[4]₂	δ^2,4 ₃ = ₂{4}₂{3}₂{4}₄	{}	{4}	{4,3}		와 같다
$\mathb{C} ^{3}$	₄[4]₂[3]₂[4]₄	δ^4,4 ₃ = ₄{4}₂{3}₂{4}₄	₄{}	₄{4}₂	₄{4}₂{3}₂		와 같다
$\mathb{C} ^{3}$	₆[4]₂[3]₂[4]₂	δ^6,2 ₃ = ₆{4}₂{3}₂{4}₂	₆{}	₆{4}₂	₆{4}₂{3}₂		or와 동일
$\mathb{C} ^{3}$	₆[4]₂[3]₂[4]₂	δ^2,6 ₃ = ₂{4}₂{3}₂{4}₆	{}	{4}	{4,3}		와 같다
$\mathb{C} ^{3}$	₆[4]₂[3]₂[4]₃	δ^6,3 ₃ = ₆{4}₂{3}₂{4}₃	₆{}	₆{4}₂	₆{4}₂{3}₂		와 같다
$\mathb{C} ^{3}$	₆[4]₂[3]₂[4]₃	δ^3,6 ₃ = ₃{4}₂{3}₂{4}₆	₃{}	₃{4}₂	₃{4}₂{3}₂		와 같다
$\mathb{C} ^{3}$	₆[4]₂[3]₂[4]₆	δ^6,6 ₃ = ₆{4}₂{3}₂{4}₆	₆{}	₆{4}₂	₆{4}₂{3}₂		와 같다

4위, 예외적인 경우
공간	그룹	3아페이로토프	꼭지점	가장자리	면	셀	판 오스 아페이로곤	메모들
$\mathb{C} ^{3}$	₂[4]₃[3]₃[3]₃	₃{3}₃{3}₃{4}₂	1	24 ₃{}	27 ₃{3}₃	2 ₃{3}₃{3}₃	₃{4}₆	와 같다
$\mathb{C} ^{3}$	₂[4]₃[3]₃[3]₃	₂{4}₃{3}₃{3}₃	2	27 {}	24 ₂{4}₃	1 ₂{4}₃{3}₃	₂{12}₃
$\mathb{C} ^{3}$	₂[3]₂[4]₃[3]₃	₂{3}₂{4}₃{3}₃	1	27 {}	72 ₂{3}₂	8 ₂{3}₂{4}₃	₂{6}₆
$\mathb{C} ^{3}$	₂[3]₂[4]₃[3]₃	₃{3}₃{4}₂{3}₂	8	72 ₃{}	27 ₃{3}₃	1 ₃{3}₃{4}₂	₃{6}₃	와 동일하다

일반복합4애피로톱스

$\mathbb {C} ^{4}$ $\mathbb {C} ^{4}$ ${\$ 에 15개의 정규 복합 애피로탑이 있다. $\mathbb {C} ^{4}$ 콕시터는 Δ로^p,r
₄ 12개를 표현하는데, 여기서 q는 $q$ = $2/(1$ – $(p$ + $r)/ pr$ 을 만족하도록 제약을 받는다 $.$ 이것들은 제품 apeirotopes로도 분해될 수 있다: = . 첫 번째 경우는 $\mathbb {R} ^{4}$ $\mathbb {R} ^{4}$ ${\$ 정전 $\mathbb {R} ^{4}$ 벌집이다. 16셀짜리 벌집과 24셀짜리 벌집이 진짜 해결책이다. 마지막 용액은 Witting polytope 원소가 생성된다.

5위
공간	그룹	4아페이로토프	꼭지점	가장자리	면	셀	4면체	판 오스 아페이로곤	메모들
$\mathb{C} ^{4}$	_p[4]₂[3]₂[3]₂[4]_r	δ^p,r ₄ = _p{4}₂{3}₂{3}₂{4}_r		_p{}	_p{4}₂	_p{4}₂{3}₂	_p{4}₂{3}₂{3}₂	_p{q}_r	와 같다
$\mathb{R} ^{4}$	₂[4]₂[3]₂[3]₂[4]₂	δ^2,2 ₄ = {4,3,3,3}		{}	{4}	{4,3}	{4,3,3}	{∞}	큐테라틱 벌집 와 같다
$\mathb{R} ^{4}$	₂[3]₂[4]₂[3]₂[3]₂ =[3,4,3,3]	{3,3,4,3}	1	12 {}	32 {3}	24 {3,3}	3 {3,3,4}		리얼 16셀 벌집 와 같다
$\mathb{R} ^{4}$	₂[3]₂[4]₂[3]₂[3]₂ =[3,4,3,3]	{3,4,3,3}	3	24 {}	32 {3}	12 {3,4}	1 {3,4,3}		리얼 24셀 벌집 와 동일하다
$\mathb{C} ^{4}$	₃[3]₃[3]₃[3]₃[3]₃	₃{3}₃{3}₃{3}₃{3}₃	1	80 ₃{}	270 ₃{3}₃	80 ₃{3}₃{3}₃	1 ₃{3}₃{3}₃{3}₃	₃{4}₆	$\mathbb {R} ^{8}$ $\mathbb {R} ^{8}$ ${\$ 표현 ${\mathbb {R}}^{8}$ ₂₁ 5

일반 복합 5-apeirotopes 이상

Δ로^p,r
_n 표현된 ^[35]C $\mathbb {C} ^{5}$ ${\$ 이상에는 $\mathbb {C} ^{5}$ $q$ = $2/(1 -$ ( $p$ + $r)/ pr)$ 를 만족하도록 제한되는 정규 복합 아페이로탑이 12개뿐입니다. 이러한 것들은 n afeirogons의 제품도 분해할 수 있다: ... = …. 첫 번째 경우는 진짜 $\mathbb {R} ^{n}$ $\mathbb {R} ^{n}$ ${\$ 하이퍼큐브 $\mathbb {R} ^{n}$ 벌집이다.

순위 6
공간	그룹	5-애피로톱스	정점	가장자리	면	셀	4면체	5면체	판 오스 아페이로곤	메모들
$\mathb{C} ^{5}$	_p[4]₂[3]₂[3]₂[3]₂[4]_r	δ^p,r ₅ = _p{4}₂{3}₂{3}₂{3}₂{4}_r		_p{}	_p{4}₂	_p{4}₂{3}₂	_p{4}₂{3}₂{3}₂	_p{4}₂{3}₂{3}₂{3}₂	_p{q}_r	와 같다
$\mathb{R} ^{5}$	₂[4]₂[3]₂[3]₂[3]₂[4]₂ =[4,3,3,3,4]	δ^2,2 ₅ = {4,3,3,3,4}		{}	{4}	{4,3}	{4,3,3}	{4,3,3,3}	{∞}	5개짜리 벌집 와 같다

판 오스 폴리곤

정규 팔면체의 가장자리와 중심 면에 있는 빨간색 사각형 판 오스 폴리곤이다.

반 오스 폴리곤은 평면의 일반 폴리곤(실제 평면 $\mathbb {R} ^{2}$ $\mathbb {R} ^{2}$ ${\$ 또는 단일 평면 $\mathbb {C} ^{2}$ $\mathbb {C} ^{2}$ ${\$ 으로, 일반 폴리토프의 가장자리와 중심부가 모두 놓여 있고 폴리토프의 원소로 형성되어 있다. 모든 일반 폴리탑이 반오오스 폴리곤을 가지고 있는 것은 아니다.

예를 들어, 실제 팔면체의 반 오스 다각형은 평면이 중심을 통과하는 세 개의 사각형이다. 대조적으로, 가장자리 대 가운데 면은 두 평방면을 대각선으로 자르고 평면에 놓여 있는 입방체의 두 가장자리는 다각형을 형성하지 않기 때문에 입방체에는 반 오스 폴리곤이 없다.

무한 벌집에는 판 오스 아페이로곤도 있다. 예를 들어 실제 사각형 타일링과 삼각 타일링에는 아페이로곤 { {} van Oss 아페이로곤이 있다.^[36]

만일 그것이 존재한다면 {q}{_rs}_t 형식의 일반 복합 폴리토프의 반 오스 폴리곤... p-cale이 있다.

비정규 복합 폴리토페스

제품 복합 폴리토페스

예제 제품 복합 폴리토프
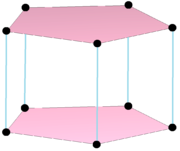복합 제품 폴리곤 또는 {}×{}}₅는 10개의 정점을 2-에지 5개, 5-에지 2개로 연결했으며, 3차원 오각형 프리즘으로 실제 표현된다.	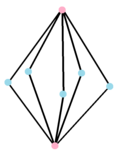듀얼 폴리곤,{}+{}₅는 원본의 가장자리를 중심으로 7개의 정점이 있으며, 10개의 가장자리로 연결되어 있다. 그것의 실제 표현은 오각형 2피라미드다.

어떤 복잡한 폴리토페스는 데카르트 제품으로 표현될 수 있다. 이 제품 폴리토프는 두 개 이상의 면으로 되어 있기 때문에 엄격하게 규칙적이지는 않지만, 직교 폴리토프가 모두 동일하다면 어떤 제품들은 정규 형태의 대칭성을 더 낮출 수 있다. 예를 들어, 2개의 1차원 폴리탑 제품 {}×{}_p 또는 2개의 1차원 폴리탑 제품이 일반 {4}₂ 또는 동일하다. {}×{}_q와 같은 보다 일반적인 제품은 4차원 p-q 듀오프람으로 실제 표현된다. 제품 폴리토프의 이중은 합 {}+{}_q로 작성할 수 있으며 4차원 p-q 듀오프라미드로 실제 표현된다. {}+{}_p은(는) 일반 복합 폴리토프 {4}_p 또는 로서 대칭이 두 배가 될 수 있다.

마찬가지로 C $\mathbb {C} ^{3}$ ${\$ ^{ $3}$ 복합 $\mathbb {C} ^{3}$ 다면체는 다음과 같은 3중 제품으로 구성될 수 있으며, 일반 일반화 큐브 {4}{₂3}_p_p₂ 또는 , 제품 {4}×{}₂_p 또는 ^[37].와 동일하다.

퀘이레겔 폴리곤

4각형 다각형은 일반 다각형을 잘라낸 것이다. Quasiregular 폴리곤에는 일반 폴리곤과 의 대체 가장자리가 포함되어 있다. Quasiregular polygon은 정규 형태의 p-edge에 p 정점을 가지고 있다.

4차 다각형 예제
_p[q]_r	₂[4]₂	₃[4]₂	₄[4]₂	₅[4]₂	₆[4]₂	₇[4]₂	₈[4]₂	₃[3]₃	₃[4]₃
정규	4 2시 30분	3시 15분	4시 16분	5시 25분	366로6길36번길	8시 49분	8로64번길
퀘이레굴라속	= 4+4 2-11	6 2시 30분 3시 15분	8 2시 30분 4시 16분	2시 10분 5시 25분	2시 12분 366로6길36번길	2시 14분 7시 49분	2시 15분 8로64번길	=	=
정규	4 2시 30분	6 2시 30분	8 2시 30분	2시 10분	2시 12분	2시 14분	2시 15분

퀘이레곤아페이로곤스

일반 아페이로곤과 그것의 일반 이중 가장자리를 교대로 하는 7개의 퀘이레곤 콤플렉스 아페이로곤이 있다. 이 아페이로곤의 꼭지점 배열은 유클리드 평면의 규칙적이고 균일한 기울기와 함께 실제적인 표현을 가지고 있다. 6{3}}6 아페이로곤의 마지막 열은 자기 이중일 뿐만 아니라 이중은 겹치는 육각 가장자리와 일치하기 때문에 그들의 퀘이레곤 형태도 겹치는 육각 가장자리로 되어 있어 다른 색과 같이 두 가지 교대로 그릴 수 없다. 자기 이중 패밀리의 대칭은 두 배로 증가시킬 수 있으므로 정규 형태와 동일한 기하학적 형태를 만들 수 있다: =

_p[q]_r	₄[4]₄	₃[6]₃	₆[3]₆
정규 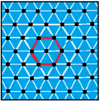또는 {q}_r
퀘이레굴라속	=	=	=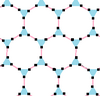
일반 이중 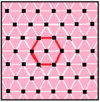또는 {q}_p

콰지레구아 다면체

3-일반화된 옥타헤드론 ₂{3}{4}₃의 잘라낸 예로서, 시작 부분에 윤곽이 있는 녹색 삼각형 면과 새 면으로 확장되는 파란색 {4},₃ 꼭지점 수치를 보여준다.

실제 다면체와 마찬가지로 복합적인 퀘이레규어 다면체는 일반 다면체의 정류(완전 잘림)로 구성될 수 있다. 정점은 일반 다면체의 중간 가장자리와 일반 다면체의 면과 그 이중은 공통 가장자리에서 교대로 배치된다.

예를 들어, p-일반화된 큐브 는 p-정점³, 3p² 가장자리 및 3p p-일반화된 사각면을 가지고 있는 반면, p-일반화된 8각형 면은 3p 정점, 3p² 가장자리 및 p 삼각형³ 면을 가지고 있다. 중간 정사각형 형태인 p-일반화된 큐보타헤드론은 정점이² 3p, 가장자리가³ 3p, 면이 3p+p이다³.

또한 Hessian 다면체의 정류는 , 규칙적인 복합 다면체의 기하학을 공유하는 Quasiregular 형식입니다.

쿼시레겔러티브
일반화 큐브/옥타헤드라						헤시안 다면체
	p=2 (진짜)	p=3	p=4	p=5	p=6	헤시안 다면체
일반화 정육면체의 (정규직)	큐브 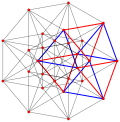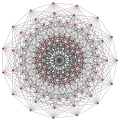, 8 정점, 12개의 2-정점, 6개의 얼굴.	, 27정점, 27정점, 27정점, 9면, 1면 파란색과 빨간색	, 64정점, 48 4정점, 12면.	, 125정점, 75 5정점, 15면.	, 216 정점, 108 6-118, 18면.	, 27정점, 72정점, 27정면.
일반화 큐보타헤드라 (정량형)	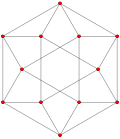큐폭타헤드론 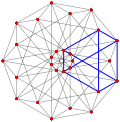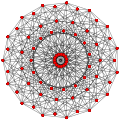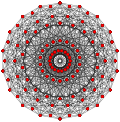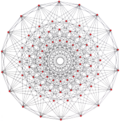, 12 정점, 24개의 2-정점 및 6+8 면.	, 27정점, 81 2정점, 9+27면, 1면 파란색	, 정점 48개, 2-162개, 12+64개 면(한 면 파란색)	, 75 정점, 375 2-정점, 15+125 면.	, 108 정점, 648 2-정점, 18+216 면.	= , 72정점, 216 3각형 및 54면.
일반화 팔면체 (정규직)	팔면체 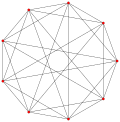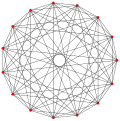, 6정점, 12정점, 8 {3}면.	, 9정점, 27 2정점, 27 {3}면.	, 12정점, 48정점, 64 {3}면.	, 15정점, 75정점, 125 {3}면.	, 18정점, 108 2정점, 216 {3}면.	, 27정점, 72정점, 27정면.

기간 2의 단일 반사가 있는 기타 복합 폴리토피

다른 비정규 복합 폴리토페스는 선형 Coxeter 그래프를 만들지 않는 단일 반사 그룹 내에서 구성할 수 있다. 루프가 있는 Coxeter 다이어그램에서 Coxeter는 또는 기호(1 1 1)와 그룹[³1₁ 1 1]³^[38]^[39]과 같은 특수 기간 내부를 표시한다. 이러한 복잡한 폴리토프는 몇 가지 경우를 넘어서서 체계적으로 탐구되지 않았다.

그룹은₃ 모든₁₁² 순서 2: R = R₁² = R₃² = (RR₁₂)³ = (RR₂₃)³ = (RR₃₁)³ = (RRR) = (RRR) = (RRRR)^p = (RRRR₁₂₃₁) = (RRRR) = 1. period p는 실제 R $\mathbb {R} ^{4}$ ${\$ 에서 이중 회전으로 볼 수 있다 $\mathbb {R} ^{4}$

반사에 의해 생성된 모든 와이토프 구조, 폴리토페와 마찬가지로 단일 링 Coxeter 다이어그램 폴리토프의 정점 수는 링 노드가 제거되는 서브그룹의 순서로 나눈 순서와 같다. 예를 들어, 실제 큐브에는 8각 대칭 순서가 48인 Coxeter 다이어그램과 6 부분군 대칭 순서가 있으므로 큐브의 정점 수는 48/6=8이다. 면은 예를 들어 큐브에 대해 링이 있는 노드에서 가장 먼 하나의 노드를 제거하여 생성된다. 꼭지점 수치는 링 노드를 제거하고 하나 이상의 연결된 노드를 울림으로써 생성되며 큐브에 대해 생성된다.

Coxeter는 다음과 같은 기호로 이러한 그룹을 나타낸다. 일부 그룹은 순서는 같지만 구조가 달라 복잡한 폴리토페스에서 동일한 꼭지점 배열을 정의하지만 p≠3과 같이 다른 가장자리 및 상위 원소를 정의한다.^[40]

단일 반사에 의해 생성된 그룹
콕시터 다이어그램	주문	Shephard and Todd의 표 7에 있는 기호 또는 위치
, ( 및 ) , , ...	p^{n − 1} n!, p ≥ 3	G(p, p, n), [p], [1 1 1],^p [1 1(n-2)]^p³
,	72·6!, 108·9!	번호 33, 34, [1 2 2],³ [1 2 3]³
, ( 및 ), ( 및 )	14·4!, 3·6!, 64·5!	24번, 27번, 29번

Coxeter는 이 복잡한 다면체들 중 몇몇을 거의 규칙적으로 부른다. 왜냐하면 그것들은 규칙적인 면과 꼭지점 수치를 가지고 있기 때문이다. 첫 번째는 C $\mathbb {C} ^{3}$ ${\$ 에서 일반화된 교차 폴리토프의 하부 대칭 형태다 $\mathbb {C} ^{3}$ 두 번째는 부분 일반화된 입방체로, p-edge를 하나의 정점으로 줄여 일반적인 2-edge를 남긴다. 그 중 3개는 $\mathbb {R} ^{4}$ $\mathbb {R} ^{4}$ ${\$ 의 유한 일반 스큐 다면체와 관련이 있다 $\mathbb {R} ^{4}$

거의 규칙적인 복합 다면체^[41]

공간	그룹	주문	콕시터 기호	정점	가장자리	얼굴	꼭지점 형상을 나타내다	메모들
$\mathb{C} ^{3}$	[1 1 1^p]³ p=2,3,4...	6p²	(1 1 1₁^p)³	3p	3p²	{3}	{2p}	셰퍼드 기호(1;^p 1₁) β^p ₃ =과 동일
$\mathb{C} ^{3}$	[1 1 1^p]³ p=2,3,4...	6p²	(1₁ 1 1^p)³	p²		{3}	{6}	셰퍼드 기호(1₁;^p 1) 1/p γ^p ₃
$\mathb{R} ^{3}$	[1 1 1²]³	24	(1 1 1₁²)³	6	12	8 {3}	{4}	β² ₃ = = 실제 옥타헤드론과 동일
$\mathb{R} ^{3}$	[1 1 1²]³	24	(1₁ 1 1²)³	4	6	4 {3}	{3}	1/2 γ² ₃ = α₃ = 실제 사면체
$\mathb{C} ^{3}$	[1 1 1]³	54	(1 1 1₁)³	9	27	{3}	{6}	셰퍼드 기호(1;³ 1₁) β³ ₃ =과 동일
$\mathb{C} ^{3}$	[1 1 1]³	54	(1₁ 1 1)³	9	27	{3}	{6}	셰퍼드 기호(1₁;³ 1) 1/3 γ³ ₃ = β³ ₃
$\mathb{C} ^{3}$	[1 1 1⁴]³	96	(1 1 1₁⁴)³	12	48	{3}	{8}	셰퍼드 기호(1;⁴ 1₁) β⁴ ₃ =과 동일
$\mathb{C} ^{3}$	[1 1 1⁴]³	96	(1₁ 1 1⁴)³	16		{3}	{6}	셰퍼드 기호(1₁;⁴ 1) 1/4 γ⁴ ₃
$\mathb{C} ^{3}$	[1 1 1⁵]³	150	(1 1 1₁⁵)³	15	75	{3}	{10}	셰퍼드 기호(1;⁵ 1₁) β⁵ ₃ =과 동일
$\mathb{C} ^{3}$	[1 1 1⁵]³	150	(1₁ 1 1⁵)³	25		{3}	{6}	셰퍼드 기호(1₁;⁵ 1) 1/5 γ⁵ ₃
$\mathb{C} ^{3}$	[1 1 1⁶]³	216	(1 1 1₁⁶)³	18	216	{3}	{12}	셰퍼드 기호(1;⁶ 1₁) β⁶ ₃ =과 동일
$\mathb{C} ^{3}$	[1 1 1⁶]³	216	(1₁ 1 1⁶)³	36		{3}	{6}	셰퍼드 기호(1₁;⁶ 1) 1/6 γ⁶ ₃
$\mathb{C} ^{3}$	[1 1 1⁴]⁴	336	(1 1 1₁⁴)⁴	42	168	112 {3}	{8}	$\mathbb {R} ^{4}$ $\mathbb {R} ^{4}$ ${\$ 표현 $\mathbb {R} ^{4}$ {3,8,4} = {3,8}₈
$\mathb{C} ^{3}$	[1 1 1⁴]⁴	336	(1₁ 1 1⁴)⁴	56		{3}	{6}
$\mathb{C} ^{3}$	[1 1 1⁵]⁴	2160	(1 1 1₁⁵)⁴	216	1080	720 {3}	{10}	$\mathbb {R} ^{4}$ $\mathbb {R} ^{4}$ ${\$ {3,10,4} = {3,10}₈
$\mathb{C} ^{3}$	[1 1 1⁵]⁴		(1₁ 1 1⁵)⁴	360		{3}	{6}
$\mathb{C} ^{3}$	[1 1 1⁴]⁵		(1 1 1₁⁴)⁵	270	1080	720 {3}	{8}	$\mathbb {R} ^{4}$ $\mathbb {R} ^{4}$ ${\$ 표현 $\mathbb {R} ^{4}$ {3,8,5} = {3,8}₁₀
$\mathb{C} ^{3}$	[1 1 1⁴]⁵		(1₁ 1 1⁴)⁵	360		{3}	{6}

Coxeter는 예를 들어 이 세 가지와 같은 반독점 구조를 가진 다른 그룹을 정의한다. 첫 번째는 1966년 피터 맥뮬런에 의해 발견되어 그려졌다.^[42]

보다 일반적인 복합 다면체^[41]

공간	그룹	주문	콕시터 기호	정점	가장자리	얼굴	꼭지점 형상을 나타내다	메모들
$\mathb{C} ^{3}$	[1 1⁴ 1⁴]⁽³⁾	336	(1₁ 1⁴ 1⁴)⁽³⁾	56	168	84 {4}	{6}	$\mathbb {R} ^{4}$ $\mathbb {R} ^{4}$ ${\$ {4}표현 $\mathbb {R} ^{4}$ {4,6,3} = {4,6}₆
$\mathb{C} ^{3}$	[1⁵ 1⁴ 1⁴]⁽³⁾	2160	(1₁⁵ 1⁴ 1⁴)⁽³⁾	216	1080	540 {4}	{10}	$\mathbb {R} ^{4}$ $\mathbb {R} ^{4}$ ${\$ 표현 {4},10,3} = {4,10}₆
$\mathb{C} ^{3}$	[1⁴ 1⁵ 1⁵]⁽³⁾	2160	(1₁⁴ 1⁵ 1⁵)⁽³⁾	270	1080	432 {5}	{8}	$\mathbb {R} ^{4}$ $\mathbb {R} ^{4}$ ${\$ 표현 $\mathbb {R} ^{4}$ {5,8,3} = {5,8}₆

일부 복잡한 4폴리토프^[41]

공간	그룹	주문	콕시터 기호	정점	기타 요소들	세포	메모들
$\mathb{C} ^{4}$	[1 1 2^p]³ p=2,3,4...	24p³	(1 1 2₂^p)³	4p			셰퍼드(^p2 1₂, 1) β^p ₄ =과 동일
$\mathb{C} ^{4}$	[1 1 2^p]³ p=2,3,4...	24p³	(1₁ 1 2^p )³	p³			셰퍼드(^p2 1, 1₁) 1/p γ^p ₄
$\mathb{R} ^{4}$	[1 1 2²]³ =[3^1,1,1]	192	(1 1 2₂²)³	8	24개의 가장자리 32면	16	β² ₄ = , 실제 16-cell
$\mathb{R} ^{4}$	[1 1 2²]³ =[3^1,1,1]	192	(1₁ 1 2² )³	8	24개의 가장자리 32면	16	1/2² ₄ ³ = β² ₄, 실제 16-cell
$\mathb{C} ^{4}$	[1 1 2]³	648	(1 1 2₂)³	12			셰퍼드(³2 1₂, 1) β³ ₄ =과 동일
$\mathb{C} ^{4}$	[1 1 2]³	648	(1₁ 1 2³)³	27			셰퍼드(³2 1, 1₁) 1/3 γ³ ₄
$\mathb{C} ^{4}$	[1 1 2⁴]³	1536	(1 1 2₂⁴)³	16			셰퍼드(⁴2 1₂, 1) β⁴ ₄ =과 동일
$\mathb{C} ^{4}$	[1 1 2⁴]³	1536	(1₁ 1 2⁴ )³	64			셰퍼드(⁴2 1, 1₁) 1/4 γ⁴ ₄
$\mathb{C} ^{4}$	[1⁴ 1 2]³	7680	(2₂ 1⁴ 1)³	80			셰퍼드(⁴2 1₂, 1)
			(1₁⁴ 1 2)³	160			셰퍼드(⁴2 1, 1₁)
			(1₁ 1⁴ 2)³	320			셰퍼드(⁴2 1₁, 1)
$\mathb{C} ^{4}$	[1 1 2]⁴		(1 1 2₂)⁴	80	640 엣지 삼각형 1280개	640
$\mathb{C} ^{4}$	[1 1 2]⁴		(1₁ 1 2)⁴	320

일부 복잡한 5폴리토프^[41]

공간	그룹	주문	콕시터 기호	정점	메모들
$\mathb{C} ^{5}$	[1 1 3^p]³ p=2,3,4...	120펜스⁴	(1 1 3₃^p)³	5p	셰퍼드(3₃.1;^p 1) β^p ₅ =과 동일
$\mathb{C} ^{5}$	[1 1 3^p]³ p=2,3,4...	120펜스⁴	(1₁ 1 3^p)³	p⁴	셰퍼드(3.1;^p 1₁) 1/p γ^p ₅
$\mathb{C} ^{5}$	[2 2 1]³	51840	(2 1 2₂)³	80	셰퍼드(³2 1, 2₂)
$\mathb{C} ^{5}$	[2 2 1]³	51840	(2 1₁ 2)³	432	셰퍼드(³2 1₁, 2)

어떤 복잡한 6폴리토프^[41]

공간	그룹	주문	콕시터 기호	정점	메모들
$\mathb{C} ^{6}$	[1 1 4^p]³ p=2,3,4...	720p⁵	(1 1 4₄^p)³	6p	셰퍼드 (4₄ 1, ^p1) β^p ₆ =과 동일
$\mathb{C} ^{6}$	[1 1 4^p]³ p=2,3,4...	720p⁵	(1₁ 1 4^p)³	p⁵	셰퍼드 (4 1₁, ^p1) 1/p γ^p ₆
$\mathb{C} ^{6}$	[1 2 3]³	39191040	(2 1 3₃)³	756	셰퍼드(³2 1, 3₃)
			(2₂ 1 3)³	4032	셰퍼드(³2 1₂, 3)
			(2 1₁ 3)³	54432	셰퍼드(³2 1, 3₁)

시각화

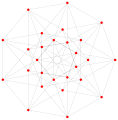
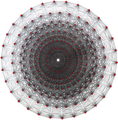
(1 1 1₁⁴) ⁴정점 42개, 가장자리 168개 및 이 14-곤 돌출부에서 볼 수 있는 112개의 삼각형 면을 가지고 있다.
(1⁴ 1⁴ 1₁) ⁽³⁾정점 56개, 가장자리 168개 및 정사각형 면 84개를 가지고 있으며, 이 14-곤 투영에서 볼 수 있다.
(1 1 2₂),⁴ 정점 80개, 가장자리 640개, 삼각면 1280개, 사면 세포 640개를 가지고 있으며, 이 20곤 투영에서 볼 수 있다.^[43]

참고 항목

쿼터니온 폴리토프

메모들

^ 피터 올릭, 빅터 라이너, 앤 5세 셰플러. 셰퍼드 그룹의 간판 표시. 수탈리스체 안날렌. 2002년 3월 322권 발행 3페이지 477-492. DOI:10.1007/s002080200001 [1]
^ Coxeter, 일반 복합 폴리토페스, 페이지 115
^ Coxeter, 일반 복합 폴리토페스, 11.3 Petrie Polygon, 11.3 Petrie Polygon, 어떤 비별의 일반 복합 폴리곤의 반사를 발생시키는 두 제품의 곱에 대해 국기(O₀,OO₀₁)의 궤도에 의해 형성된 단순한 h-곤, p₁{q}p₂.
^ 복합 일반 폴리토페스,11.1 일반 복합 폴리곤 페이지 103
^ 1952년 셰퍼드(Shephard, 1952년) : "폴리포프 내부의 개념을 도출하는 것은 이것과 같은 고려에서 비롯된 것이며, 숫자가 그렇게 순서가 정해질 수 없는 단일 공간에서는 그러한 내부 개념이 불가능하다는 것을 알 수 있을 것이다. [Para break] 자... 단일 다상체를 구성으로 고려해야 한다"고 말했다.
^ Coxeter, 일반 복합 폴리토페스, 페이지 96
^ Coxeter, 일반 복합 폴리토페스, p. xiv
^ Coxeter, 복합 일반 폴리토페스, 페이지 177, 표 III
^ 레러 & 테일러 2009, 페이지 87
^ Coxeter, 일반 복합 폴리토페스, 표 IV. 정규 다각형 178-179페이지
^ 복합 폴리토페스, 8.9 2차원 케이스, 페이지 88
^ 일반 복합 폴리토페스, 콕시터, 페이지 177-179
^ ^a ^b Coxeter, 일반 복합 폴리토페스, 페이지 108
^ Coxeter, 일반 복합 폴리토페스, 페이지 109
^ Coxeter, 일반 복합 폴리토페스, 페이지 111
^ Coxeter, 일반 복합 폴리토페스, 페이지 30 다이어그램 및 페이지 47 지수 8개 3개 에지
^ ^a ^b Coxeter, 일반 복합 폴리토페스, 페이지 110
^ Coxeter, 일반 복합 폴리토페스, 페이지 48
^ Coxeter, 일반 복합 폴리토페스, 페이지 49
^ Coxeter, 일반 복합 폴리토페스, 페이지 116–140.
^ ^a ^b Coxeter, 일반 복합 폴리토페스, 페이지 118–119.
^ 복합 일반 폴리토페스, 페이지
^ ^a ^b Coxeter, 일반 복합 폴리탑, 표 V. 비성형 일반 다면체와 4-폴리토프. 페이지 180.
^ Coxeter, Kaleidotic - H.S.M. Coxeter의 선별된 글, Paper 25 단일 반사 그룹 간의 놀라운 관계, 페이지 431.
^ ^a ^b Coxeter, 일반 복합 폴리토페스, 페이지 131
^ Coxeter, 일반 복합 폴리토페스, 페이지 126
^ Coxeter, 일반 복합 폴리토페스, 페이지 125
^ Coxeter, 일반 복합 폴리토페스, 표 VI. 일반 꿀벌집. 180 페이지.
^ 복합 일반 폴리토프, 페이지 174
^ Coxeter, 일반 복합 폴리토페스, 표 VI. 일반 꿀벌집. 페이지 111, 136.
^ Coxeter, 일반 복합 폴리토페스, 표 IV. 정규 다각형 178-179페이지
^ Coxeter, 일반 복합 폴리토페스, 11.6 Afeirogons, 페이지 111-112
^ Coxeter, 복합 일반 폴리토페스, 페이지 140
^ Coxeter, 일반 복합 폴리토페스, 페이지 139-140
^ 복합 일반 폴리토페스, 페이지 146
^ 복합 일반 폴리토페스, 페이지 141
^ Coxeter, 일반 복합 폴리토페스, 페이지 118–119, 138.
^ Coxeter, 정규 복합 폴리토페스, 14장, 거의 정규 폴리토페스, 페이지 156–174.
^ Coxeter, 1956년 2월 2일의 유니터리 반사에 의해 생성된 그룹
^ Coxeter, Unital Reflections에 의해 생성된 유한 집단, 1966, 4 그래픽 표기법, N-Unitarity Reflections에 의해 생성된 n-차원 그룹 표. 페이지 422-423
^ ^a ^b ^c ^d ^e Coxeter, 2주기(1956년), 표 III: 일부 복합 폴리토페스, 페이지 413의 유니터리 반사에 의해 생성된 그룹
^ Coxeter, Complex Regular Polytopes, (1991), 14.6 McMullen의 두 다면체 84면, 페이지.166-171
^ Coxeter, 복합 일반 폴리탑, 페이지 172-173

참조

Coxeter, H. S. M. 및 Moser, W. O. J.; 이산 그룹을 위한 생성자와 관계(1965) esp 67-80.
Coxeter, H.S.M. (1991), Regular Complex Polytopes, Cambridge University Press, ISBN 0-521-39490-2
Coxeter, H. S. M. and Shephard, G.C.; 복잡한 폴리토페스 계열의 초상화, 레오나르도 Vol 25, No 3/4, (1992), 페이지 239–244,
셰퍼드, G.C.; 규칙적인 복합 폴리토페스, 프로크. 런던 수학. Soc. 시리즈 3, 2, (1952), 페이지 82–97.
G. C. 셰퍼드, J. A. Todd, 유한한 단일 반사 그룹, 캐나다 수학 저널. 6(1954년), 274-304 [2]^{[permanent dead link]}
구스타프 1세 레러와 도널드 E. 테일러, 케임브리지 대학 출판부, 2009년 유니티 리플렉션 그룹

추가 읽기

F. Arthur Sherk, Peter McMullen, Anthony C. 톰슨과 아시아 이비치 와이스, 편집자: 케일리디스코어 - 단일반사로 생성된 H.S.M. Coxeter, Paper 25, Finitial 그룹, p 415-425, John Wiley, 1995, ISBN 0-471-01003-0
McMullen, Peter; Schulte, Egon (December 2002), Abstract Regular Polytopes (1st ed.), Cambridge University Press, ISBN 0-521-81496-0 제9장 유니터리 그룹과 에르미타르의 양식, 페이지 289-298

[1] 피터 올릭, 빅터 라이너, 앤 5세 셰플러. 셰퍼드 그룹의 간판 표시. 수탈리스체 안날렌. 2002년 3월 322권 발행 3페이지 477-492. DOI:10.1007/s002080200001 [1]

[2] Coxeter, 일반 복합 폴리토페스, 페이지 115

[3] Coxeter, 일반 복합 폴리토페스, 11.3 Petrie Polygon, 11.3 Petrie Polygon, 어떤 비별의 일반 복합 폴리곤의 반사를 발생시키는 두 제품의 곱에 대해 국기(O₀,OO₀₁)의 궤도에 의해 형성된 단순한 h-곤, p₁{q}p₂.

[4] 복합 일반 폴리토페스,11.1 일반 복합 폴리곤 페이지 103

[5] 1952년 셰퍼드(Shephard, 1952년) : "폴리포프 내부의 개념을 도출하는 것은 이것과 같은 고려에서 비롯된 것이며, 숫자가 그렇게 순서가 정해질 수 없는 단일 공간에서는 그러한 내부 개념이 불가능하다는 것을 알 수 있을 것이다. [Para break] 자... 단일 다상체를 구성으로 고려해야 한다"고 말했다.

[6] Coxeter, 일반 복합 폴리토페스, 페이지 96

[7] Coxeter, 일반 복합 폴리토페스, p. xiv

[8] Coxeter, 복합 일반 폴리토페스, 페이지 177, 표 III

[9] 레러 & 테일러 2009, 페이지 87

[10] Coxeter, 일반 복합 폴리토페스, 표 IV. 정규 다각형 178-179페이지

[11] 복합 폴리토페스, 8.9 2차원 케이스, 페이지 88

[12] 일반 복합 폴리토페스, 콕시터, 페이지 177-179

[:0-13] Coxeter, 일반 복합 폴리토페스, 페이지 108

[14] Coxeter, 일반 복합 폴리토페스, 페이지 109

[15] Coxeter, 일반 복합 폴리토페스, 페이지 111

[16] Coxeter, 일반 복합 폴리토페스, 페이지 30 다이어그램 및 페이지 47 지수 8개 3개 에지

[:5-17] Coxeter, 일반 복합 폴리토페스, 페이지 110

[18] Coxeter, 일반 복합 폴리토페스, 페이지 48

[19] Coxeter, 일반 복합 폴리토페스, 페이지 49

[20] Coxeter, 일반 복합 폴리토페스, 페이지 116–140.

[:4-21] Coxeter, 일반 복합 폴리토페스, 페이지 118–119.

[22] 복합 일반 폴리토페스, 페이지

[:3-23] Coxeter, 일반 복합 폴리탑, 표 V. 비성형 일반 다면체와 4-폴리토프. 페이지 180.

[24] Coxeter, Kaleidotic - H.S.M. Coxeter의 선별된 글, Paper 25 단일 반사 그룹 간의 놀라운 관계, 페이지 431.

[:2-25] Coxeter, 일반 복합 폴리토페스, 페이지 131

[26] Coxeter, 일반 복합 폴리토페스, 페이지 126

[27] Coxeter, 일반 복합 폴리토페스, 페이지 125

[28] Coxeter, 일반 복합 폴리토페스, 표 VI. 일반 꿀벌집. 180 페이지.

[29] 복합 일반 폴리토프, 페이지 174

[30] Coxeter, 일반 복합 폴리토페스, 표 VI. 일반 꿀벌집. 페이지 111, 136.

[31] Coxeter, 일반 복합 폴리토페스, 표 IV. 정규 다각형 178-179페이지

[32] Coxeter, 일반 복합 폴리토페스, 11.6 Afeirogons, 페이지 111-112

[33] Coxeter, 복합 일반 폴리토페스, 페이지 140

[34] Coxeter, 일반 복합 폴리토페스, 페이지 139-140

[35] 복합 일반 폴리토페스, 페이지 146

[36] 복합 일반 폴리토페스, 페이지 141

[37] Coxeter, 일반 복합 폴리토페스, 페이지 118–119, 138.

[38] Coxeter, 정규 복합 폴리토페스, 14장, 거의 정규 폴리토페스, 페이지 156–174.

[39] Coxeter, 1956년 2월 2일의 유니터리 반사에 의해 생성된 그룹

[40] Coxeter, Unital Reflections에 의해 생성된 유한 집단, 1966, 4 그래픽 표기법, N-Unitarity Reflections에 의해 생성된 n-차원 그룹 표. 페이지 422-423

[:1-41] Coxeter, 2주기(1956년), 표 III: 일부 복합 폴리토페스, 페이지 413의 유니터리 반사에 의해 생성된 그룹

[42] Coxeter, Complex Regular Polytopes, (1991), 14.6 McMullen의 두 다면체 84면, 페이지.166-171

[43] Coxeter, 복합 일반 폴리탑, 페이지 172-173

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

Search